ON BINARY SIMILARITY MEASURES FOR

PRIVACY-PRESERVING TOP-N RECOMMENDATIONS

∗

Alper Bilge, Cihan Kaleli and Huseyin Polat

Computer Engineering Department, Anadolu University, Eskisehir, 26470 Turkey

Keywords:

Collaborative ﬁltering, Top-N recommendation, Binary similarity measures, Privacy, accuracy.

Abstract:

Collaborative ﬁltering (CF) algorithms fundamentally depend on similarities between users and/or items to

predict individual preferences. There are various binary similarity measures like Kulzinsky, Sokal-Michener,

Yule, and so on to estimate the relation between two binary vectors. Although binary ratings-based CF al-

gorithms are utilized, there remains work to be conducted to compare the performances of binary similarity

measures. Moreover, the success of CF systems enormously depend on reliable and truthful data collected

from many customers, which can only be achieved if individual users’ privacy is protected. In this study, we

compare eight binary similarity measures in terms of accuracy while providing top-N recommendations. We

scrutinize how such measures perform with privacy-preserving top-N recommendation process. We perform

real data-based experiments. Our results show that Dice and Jaccard measures provide the best outcomes.

1 INTRODUCTION

Collaborative ﬁltering (CF) techniques are widely

used in e-commerce to provide recommendations. CF

has many important applications in e-commerce, di-

rect recommendations, and search engines (Canny,

2002). CF systems predict the preferences of an ac-

tive user (a), based on the preferences of other users.

The idea is that a will prefer those items that like-

minded users prefer, or that dissimilar users do not.

Users’ ratings about various products might be binary

showing whether a user likes an item or not.

Detecting and interpreting the relation between

users and/or items is the heart of CF processes. Sev-

eral similarity measures operating on numerical data

have been suggested (Sarwar et al., 2001). However,

in case of binary data, neither calculating the linear

correlation nor gauging the angle between two vec-

tors do not make sense, because they consist of only

binary ratings as preferences. Thus, binary similarity

measures focus on matches to determine the similarity

between two vectors. A match occurs if an item is co-

rated by two users for user-based similarity calcula-

tions or if two items are rated by an individual user for

item-based similarity calculations. As long as binary

vectors are considered, there are three categories of

∗

This work was supported by the Grant 108E221 from

TUBITAK.

matches: (i) positive matches, (ii) negative matches,

and (iii) opposite matches. Different similarity mea-

sures interpret the importance of those matches and

state different expressions to quantify similarity.

Users might refuse to provide data at all or hes-

itate to provide their true data due to privacy con-

cerns (Cranor, 2003). Users might want to hide their

ratings and the products they bought. Thus, users

mask their data to prevent the server from learning

true ratings and rated items. With increasing pri-

vacy concerns, privacy-preservingcollaborative ﬁlter-

ing (PPCF) schemes have been receiving increasing

attention (Kaleli and Polat, 2010; Polat and Du, 2008;

Canny, 2002; Kaleli and Polat, 2007).

CF systems provide top-N recommenda-

tions (Huang and Huang, 2009). Producing

such services require forming a neighborhood of

similar users and/or items. The best similar users

and/or items are determined based on the similarity

between users and/or items. For the success of top-N

recommendations, it is crucial to utilize the best

similarity measure.

2 RELATED WORKS

Zhang and Srihari (Zhang and Srihari, 2003) exam-

ines a number of binary vector similarity/dissimilarity

299

Bilge A., Kaleli C. and Polat H. (2010).

ON BINARY SIMILARITY MEASURES FOR PRIVACY-PRESERVING TOP-N RECOMMENDATIONS.

In Proceedings of the 5th International Conference on Software and Data Technologies, pages 299-304

DOI: 10.5220/0002938702990304

 SciTePress

measures for their recognition capability in hand-

written pattern recognition, how to choose a similar-

ity/dissimilarity measure, and how to combine hybrid

features. Cha et al. (Cha et al., 2005) review, cate-

gorize, and evaluate several binary vector similarity

measures for character recognition issues.

Karypis (Karypis, 2001) presents an item-based

top-N recommendation algorithm that ﬁrst deter-

mines the similarities between the items and then uses

them to identify the set of items to be recommended.

Kwon (Kwon, 2008) proposes new approaches, which

can improveitem selection by taking into account rat-

ing variance. Blattner (Blattner, 2009) proposes a ran-

dom walk-based top-N recommendation algorithm.

His method outperforms other state of the art algo-

rithms in terms of recall. Jamali and Ester (Jamali

and Ester, 2009) propose novel methods to produce

top-N recommendation services using a trust network

to improve the quality of recommendations.

Polat and Du (Polat and Du, 2005) propose a

scheme for binary ratings-based top-N recommenda-

tion on horizontally partitioned data while preserving

data owners’ privacy. In another study, the authors

introduce privacy-preservingtop-N recommendations

on distributed data to overcome inadequate data and

sparseness problems of CF (Polat and Du, 2008).

Kaleli and Polat (Kaleli and Polat, 2007) propose

to employ randomized response techniques (RRT) to

protect users privacy while producing accurate refer-

rals using na¨ıve Bayesian classiﬁer (NBC).

Unlike the studies conducted so far, our goal is

to compare binary similarity measures for top-N rec-

ommendations. Furthermore, we want to investigate

how they behave while offering top-N recommenda-

tions with privacy concerns. We ﬁnally determine the

best one (s) that can be used for better top-N recom-

mendations with or without privacy concerns.

3 TOP-N RECOMMENDATION

ALGORITHM AND BINARY

SIMILARITY MEASURES

Karypis (Karypis, 2001) propose an item-based top-N

recommendation algorithm assuming that a user will

probably like an item similar to the ones she has al-

ready purchased. In his model, the users are repre-

sented with their transaction data in which the pre-

viously purchased items are marked as a “1” and re-

maining ones with a “0”. During the model build-

ing phase, for each item j, the k most similar items

{ j

, j

,..., j

} are computed, and their corresponding

similarities {s

,...,s

} are recorded. For each

customer that has purchased a set U of items, this in-

formation is used to compute the top-N recommended

items, as follows. First, the set C of candidate recom-

mended items are identiﬁed by taking the union of

the k most similar items for each item j ∈ U, and re-

moving from the union any items that are already in

U. Then, for each item c ∈ C, its similarity to the

set U as the sum of the similarities between all the

items j ∈ U and c is computed, using only the k most

similar items of j. Finally, the items in C are sorted

in non-increasing order with respect to that similarity,

and the ﬁrst N items are selected as the top-N recom-

mendations.

Let x and y be two binary vectors

in a z-dimensional space, and let A, B,

C, D, and σ be deﬁned, as follows:

A = S

(x,y)

B = S

(x,y)

C = S

(x,y)

D = S

(x,y)

σ = [(A+ B)(A+C)(B + D)(C+ D)]

1/2

where S

is the number of occurrences of commonly

rated items with i in the ﬁrst pattern and j in the sec-

ond pattern. Eight binary similarity measures are de-

ﬁned in Table 1 (Gan et al., 2007).

Table 1: Binary Similarity Measures.

Similarity Measure Deﬁnition Range

Dice

2A+B+C

[0,

]

Jaccard

A+B+C

[0, 1]

Kulzinsky

B+C

[0,∞)

Pearson

AD−BC

[−1,1)

Rogers-Tanimoto (RT)

A+D

A+2(B+C)+D

[0, 1]

Russell-Rao (RR)

[0, 1]

Sokal-Michener (SM)

A+D

[0, 1]

Yule

AD−BC

AD+BC

[-1, 1]

4 PRODUCING PRIVATE TOP-N

RECOMMENDATIONS ON

BINARY DATA

We utilize the algorithm proposed by

Karypis (Karypis, 2001). We use users’ ratings

about products they bought. The set contains users’

ratings as “1” (like), “0” (dislike), or blank cells.

Since customers buy or rate a small number of

products given an entire item set, the database is a

very sparse set. In the algorithm, U contains those

items that a user bought or showed interest. In other

words, we propose to deal with actual user-item

rating matrix in which purchased and liked items are

ICSOFT 2010 - 5th International Conference on Software and Data Technologies

300

marked as “1” and purchased and disliked items are

marked as “0”. In addition to using binary ratings, we

focus on how to offer top-N recommendations with

privacy while comparing various binary similarity

measures. In the following subsections, we explain

the each step of the proposed scheme in detail.

4.1 Data Perturbation and Collection

Traditional CF algorithms fail to protect users’ pri-

vacy. Due to privacy concerns, customers might

refuse to give data at all or give false data. If privacy

measures are provided, they might feel more comfort-

able to provide their true preferences. Thus, they dis-

guise their ratings using RRT before they send them

to the data collector or a server, as follows (Kaleli and

Polat, 2007): The server and the users choose a value

θ from the range (0,1]. Each user i uniformly ran-

domly generates a number r

over the range (0, 1].

Each user i then compares r

with θ. If r

≤ θ, then

user i sends the true data. Otherwise, she sends the

exact opposite of the ratings vector. In other words,

she changes 1s to 0s and 0s to 1s. Each user can place

their ratings into a single vector and perturb them in

the same way. However, if one rating is determined

by the server, it can learn all ratings. Thus, users can

partition the items into M groups, where the RRT is

used to perturb each group independently. Note that

M is constant and 1 < M < m, where m is the num-

ber of items. Users partition their data into M groups

in the same way; but, they mask each group indepen-

dently. This way, the server or the CF system cannot

learn the true ratings. With probability θ, the received

data is true and it is false with probability 1-θ.

Users also want to hide their rated items. Each

user might insert fake ratings into their proﬁle to avoid

referred privacy weakness. But not to reduce the ac-

curacy of the system, it is important to choose how

many fake ratings to insert. Let d

be density of the

user i vector and f

be the upper bound of ﬁlling per-

cent, f

is associated with d

and current ﬁlling per-

cent (f

) is determined as a random value over the

range (0, f

]. After determining f

, each user i inserts

fake ratings into uniformly randomly selected f

per-

cent of unrated cells. After ﬁlling some of the un-

rated items cells (e), the users utilize RRT to mask the

ﬁlled vectors as explained previously. They ﬁnally

send their perturbed data to the system. Another issue

to be addressed is protecting a’s privacy. Like other

users, a also perturbs her private data similarly.

Although we apply similar methodology to dis-

guise private data as explained in (Kaleli and Po-

lat, 2007), there are some differences. First, the au-

thors in (Kaleli and Polat, 2007) propose to use the

1-out-of-n oblivious transfer protocol to protect a’s

privacy. However, in our scheme, a disguises her

data like other users do. Second, with increasing M

values, online performance signiﬁcantly degrades in

their scheme. However, since the proposed scheme

is based on item-to-item similarities, which are esti-

mated off-line, our scheme is able to offer top-N rec-

ommendations efﬁciently even if with larger M val-

ues. Third, in their scheme, users choose f

over the

range (1,γ), where they varied γ from 0 to 100. How-

ever, we associated f

with density (d

4.2 Off-line Model Construction

Model construction includes estimating similarities

between items, sorting them in non-increasing order,

and storing them. Similarities between items are esti-

mated via eight different binary similarity measures to

distinguish between their characteristics in CF frame-

work and determine the most proper ones to employ.

Binary similarity measures compute the similarity be-

tween two binary vectors; however, D, representing

true users’ ratings, does not present. Without pri-

vacy concerns, it is trivial to estimate similarities be-

tween various binary vectors. Due to underlying data

disguising methods, it becomes a challenge to esti-

mate the same similarities from perturbed data. D

′

masked user-item matrix, is obtained after collecting

data from many users. Therefore, actual rates can-

not be determined exactly, but according to disguis-

ing scheme (number of groups, M and disguising rate,

θ), an inference can be made to estimate similarities

between features. Since S

is the occurrence of com-

monly rated items for two items’ ratings vector, S

′

represents the exact opposite of the ratings, where i

′

∈ {0, 1}. Thus, we cannot simply increment the re-

lated variable, S

, due to disguising mechanism. All

the values are correct in D

′

with a probability of θ.

Thus, to estimate S

values, all possible combinations

of the match should be considered, as follows:

i, j

= S

i, j

+ (θ× θ) = S

i, j

+ θ

′

, j

= S

′

, j

+ ((1− θ) × θ) = S

′

, j

+ θ− θ

i, j

′

= S

i, j

′

+ (θ× (1− θ)) = S

i, j

′

+ θ− θ

′

, j

′

= S

′

, j

′

+ (1− θ) × (1− θ) = S

′

, j

′

+ (1− θ)

. (1)

Since collected data are masked, for example,

when there are 1s in the ﬁrst and the second pat-

tern, S

i, j

is incremented by θ

instead of 1. Simi-

larly, other S

i, j

values are estimated from perturbed

data. Once such values are estimated, similarity val-

ues between various items can be easily estimated us-

ing the aforementioned eight similarity measures. Fi-

ON BINARY SIMILARITY MEASURES FOR PRIVACY-PRESERVING TOP-N RECOMMENDATIONS

301

nally, for each item, the k most similar items are de-

termined and stored. Such model constructed off-line

is then used to produce top-N recommendations on-

line. Since the model is generated from masked data,

it can be considered as a private model preserving in-

dividual users’ privacy.

4.3 Producing Private Top-N

Recommendations

To produce top-N recommendations, a basket of

items (U) consisting of purchased items for a and a

set of candidate items (C) containing the union of the

k most similar items (not in U) for each item j ∈ U

are created. Then, for each item c ∈ C, the relation-

ship of that item to U is computed as the sum of pre-

viously recorded similarity values of c to all items

j ∈ U. Items in C are sorted according to their re-

lationships to U and the ﬁrst N of them are selected

as a top-N recommendation list.

5 PRIVACY AND OVERHEAD

COSTS ANALYSIS

Since all the computations are performed on collected

disguised data set D

′

, users’ privacy is preservedprop-

erly. As explained in (Kaleli and Polat, 2007), privacy

can be measured with respect to the reconstruction

probability (p) with which the CF system can obtain

the true ratings vector of a user given disguised data.

With increasing p, privacy level decreases. If we in-

crease randomness, privacy enhances; however, that

makes accuracy worse. With increasing M and θ val-

ues towards 0.5, p decreases, while privacy increases.

In (Kaleli and Polat, 2007), the authors advice to in-

crease M up to ﬁve due to performance reasons. How-

ever, in our scheme, users can partition their ratings

into more than ﬁve groups because computations are

performedoff-lineand item-to-item similarities rather

than user-to-user ones are estimated. Thus, users can

achieve higher privacy level using our scheme. Due to

inserted fake ratings, the server cannot learn the rated

items. The probability of guessing the correct f

is 1

out of f, where f can be 0, d/2, d, or 2d. Similarly,

it can guess the correct value of f with probability

1/4. After guessing them, it can compute e (number

of ﬁlled cells). Finally, the probability of guessing the

e randomly selected cells among m

′

empty cells is 1

out of C

′

, where C

represents the number of ways

of picking h unordered outcomes from g possibilities

and m

′

represents the number of empty cells.

The proposed scheme is able to offer recom-

mendations efﬁciently because model construction

is done off-line. Compared to the scheme pro-

posed by (Karypis, 2001), our scheme does not cause

any additional online costs due to privacy concerns.

Online computation and communication (number of

communicationsand amount of data to be transferred)

costs do not increase. Although the users add fake rat-

ings and disguise their data and that increases compu-

tation costs performed off-line, they are not critical

for the success of CF systems.

6 ACCURACY ANALYSIS

We performed various experiments using two

well-known real data sets. We used Movie-

lens Public (MLP) and EachMovie (EM) data

sets. GroupLens at the University of Min-

nesota (www.cs.umn.edu/research/Grouplens) col-

lected MLP containing ratings of 943 users for 1,682

movies in a range of 1 to 5. EM data set (McJonese,

1997) contains ratings of 72,916 users for 1,628

movies. User ratings were recorded on a numeric six-

point scale, ranging from 0 to 1. We measured accu-

racy using recall (Karypis, 2001):

recall =

Number of hits

where n is the number of users in the experiments.

We ﬁrst transformed numerical ratings into two la-

bels (like and dislike). We then uniformly randomly

selected 1,000 users who have rated at least two pos-

itive ratings from EM and we used all 943 users in

MLP. We uniformly randomly split each set into train

and test set by randomly choosing one of the liked

items of each user as a test item. The remaining rat-

ings are used for training. We set N at 10 to produce

top-10 recommendations and set k at 10, which hap-

pens to give the promising results (Karypis, 2001).

We used eight different models constructed with each

binary similarity measure. We ran our trials 10 times

using different train and test sets. To disguise data,

we set M at 3 and θ at 0.7. We repeated data masking

100 times and presented the overall average values.

We conducted an experiment to show the differ-

ence between using transaction data (TD) and users’

ratings data (RD) to build a model. We used both

data sets generating models using all binary similar-

ity measures. We set n at 1,000 and 943 for EM and

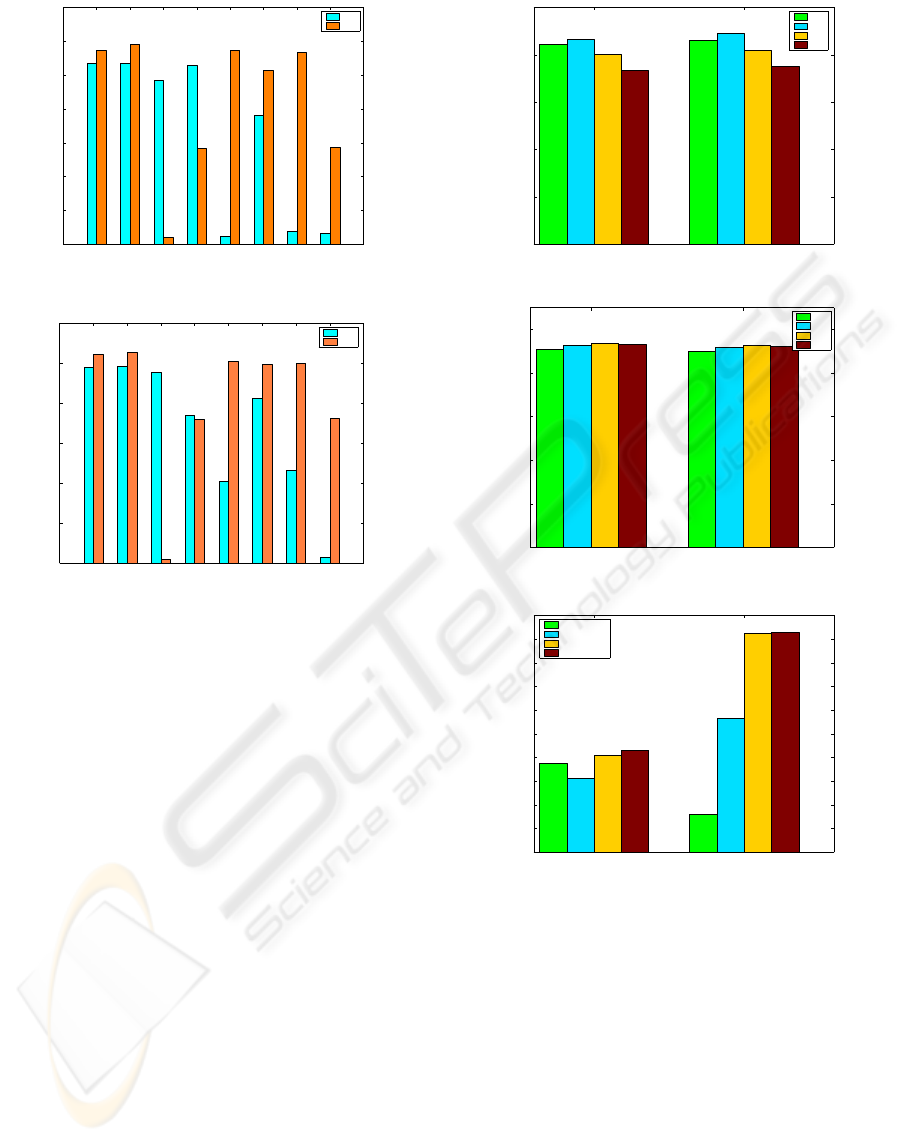
MLP, respectively. We displayed the results in Fig. 1

and Fig. 2 for both data sets.

As seen from Fig. 1 and Fig. 2, using ratings data

is usually more useful. For MLP data set, six of

eight similarity measures perform better for ratings

ICSOFT 2010 - 5th International Conference on Software and Data Technologies

302

Dice Jaccard KulzinskyPearson RT RR SM Yule

0.05

0.1

0.15

0.2

0.25

0.3

0.35

Binary Similarity Measures

Recall

Figure 1: Transaction data vs. ratings data (MLP).

Dice Jaccard Kulzinsky Pearson RT RR SM Yule

0.1

0.2

0.3

0.4

0.5

Binary Similarity Measures

Recall

Figure 2: Transaction data vs. ratings data (EM).

data than for transaction data. Only Kulzinsky and

Pearson similarity measures perform better for trans-

action data. Dice, Jaccard, RT, SM, and RR give very

promising results for ratings data. The best results are

obtained using Dice and Jaccard measures. Similarly,

for EM data set, six of eight measures achieve higher

accuracy for ratings data than transaction data. Pear-

son measure almost achieves the same result. Only

Kulzinsky gives better results for transaction data.

Like MLP data set, Dice and Jaccard measures give

the best results. Kulzinsky is not a good choice to use

with sparse sets. It is a good choice for dense sets.

To show the effects of data disguising measures,

we performed experiments while varying f from 0 to

2d. We built our model with each binary similarity

measure. We ran experiments using both data sets

and presented the overall averages for Dice and Jac-

card measures only in Fig. 3 and Fig. 4 for MLP and

EM, respectively. Note that f = 0 means that users

do not insert any fake ratings. As seen from Fig. 3,

due to RRT, accuracy decreases for both measures for

MLP. On the other hand, when f is d/2, accuracy im-

proves for both measures. For f values larger than

d/2, recall slightly diminishes. For EM, as seen from

Fig. 4, similarly, accuracy becomes worse due to pri-

vacy concerns. When users ﬁll some their empty cells

with fake ratings, recall slightly becomes better. With

Dice Jaccard

0.05

0.1

0.15

0.2

0.25

Recall

d/2

Figure 3: Recall with varying f values (MLP).

Dice Jaccard

0.1

0.2

0.3

0.4

0.5

Recall

d/2

Figure 4: Recall with varying f values (EM).

MLP EM

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0.45

0.5

Recall

125

250

500

943 & 1,000

Figure 5: Recall with varying n values.

increasing f values, the quality of the referrals im-

proves. However, such improvements are very stable.

As expected, accuracy becomes worse for both data

sets for both measures due to privacy-preservingmea-

sures. Compared to MLP, accuracy losses are smaller

for EM. However, the results are still promising.

We ﬁnally performed trials to show the effects of

varying n values on accuracy. We used Dice only in

these experimentsfor both data sets. We varied n from

125 to 943 and 1,000 for MLP and EM, respectively.

We set f at its optimum values for both data sets de-

termined previously. We follow the same method-

ology as in the previous experiments. We displayed

the overall averages for both sets in Fig. 5. As seen

in Fig. 5, accuracy increases with increasing number

ON BINARY SIMILARITY MEASURES FOR PRIVACY-PRESERVING TOP-N RECOMMENDATIONS

303

of users (n) because more reliable inferences can be

made with more data. For EM data set, recall rapidly

decreases while we changed n from 500 to 250 or 125.

Accuracy becomes stable for n values larger than 250.

Changes in recall values are more stable for MLP data

set. Recall decreases when n is increased from 125 to

250. On the other hand, it improves with increasing n

from 250 to 500 and 943.

7 CONCLUSIONS AND FUTURE

WORK

We proposed a privacy-preserving scheme to offer

top-N recommendations efﬁciently. We determined

the best similarity measures by performing experi-

ments. Utilizing ratings data is more successful for

building a model for top-N recommendations. Apart

from disguising the original data, a random ﬁlling

methodology is necessary to provide appropriate pri-

vacy preservation for hiding both ratings and rated

items. According to our results, Dice and Jaccard

measures perform the best. Kulzinsky similarity mea-

sure is not a good choice among the eight ones. It

gives the worst results. Generally speaking, six of

eight measures provide promising results. We scruti-

nized the effects of varying f values on recall. More-

over, we investigated the effect of varying n values.

We determined the optimum values of f and n.

Without privacy concerns, our results on ratings

data are very comparable with the ones presented

in (Karypis, 2001). Although accuracy diminishes

with privacy, the results are still promising compared

to the results in (Karypis, 2001). Our scheme achieves

privacy by sacriﬁcing some accuracy. Compared to

the scheme proposed by (Kaleli and Polat, 2007), our

scheme’s online performance is much more better.

As a future work, we are planning to evaluate bi-

nary similarity measures on clustering data to con-

struct a user-based model as a different research area

in CF and apply dissimilarity measures to determine if

they can perform better than similarity measures. We

will investigate whether we can reduce the accuracy

losses due to underlying privacy-preserving measures

or not by applying various improvements.

REFERENCES

Blattner, M. (2009). B-rank: A top N recommendation al-

gorithm. CoRR, arXiv:0908.2741.

Canny, J. (2002). Collaborative ﬁltering with privacy via

factor analysis. In ACM SIGIR’02, 25th Annual Inter-

national ACMSIGIR Conference on Research and De-

velopment in Information Retrieval, pages 238–245,

Tampere, Finland.

Cha, S., Yoon, S., and Tappert, C. C. (2005). On binary

similarity measures for handwritten character recog-

nition. In ICDAR’05, 8th International Conference

on Document Analysis and Recognition, pages 4–8,

Seoul, Korea.

Cranor, L. F. (2003). ‘I didn’t buy it for myself’ privacy

and E-commerce personalization. In WPES’03, ACM

Workshop on Privacy in the Electronic Society, pages

111–117, Washington, DC, USA.

Gan, G., Ma, C., and Wu, J. (2007). Data Clustering: The-

ory, Algorithms, and Applications, chapter 6 Similar-

ity and Dissimilarity Measures, pages 67 – 106. ASA-

SIAM Series on Statistics and Applied Probability.

Huang, C. L. and Huang, W. L. (2009). Handling sequential

pattern decay: Developing a two-stage collaborative

recommender system. Electron. Commer. Rec. Appl.,

8(3):117–129.

Jamali, M. and Ester, M. (2009). Using a trust network to

improve top-N recommendation. In RecSys’09, 3rd

ACM Conference on Recommender Systems, pages

181–188, New York, NY, USA.

Kaleli, C. and Polat, H. (2007). Providing private recom-

mendations using naive Bayesian classiﬁer. Advances

in Intelligent Web Mastering, 43:515–522.

Kaleli, C. and Polat, H. (2010). P2P collaborative ﬁltering

with privacy. Turkish J. Elec. Eng. and Comp. Sci.,

18(1):101–116.

Karypis, G. (2001). Evaluation of item-based top-N rec-

ommendation algorithms. In CIKM’01, 10th Inter-

national Conference on Information and Knowledge

Management, pages 247–254, Atlanta, GA, USA.

Kwon, Y. (2008). Improving top-n recommendation tech-

niques using rating variance. In RecSys’08, 2nd ACM

Conference on Recommender Systems, pages 307–

310, Lausanne, Switzerland.

McJonese, P. (1997). EachMovie collaborative ﬁltering data

set.

Polat, H. and Du, W. (2005). Privacy-preserving top-N

recommendation on horizontally partitioned data. In

WI’05, IEEE/WIC/ACM International Conference on

Web Intelligence, pages 725–731, Paris, France.

Polat, H. and Du, W. (2008). Privacy-preserving top-N rec-

ommendation on distributed data. J. Am. Soc. Inf. Sci.

Technol., 59(7):1093–1108.

Sarwar, B., Karypis, G., Konstan, J. A., and Riedl, J. T.

(2001). Item-based collaborative ﬁltering recommen-

dation algorithms. In WWW’10, 10th International

World Wide Web Conference, pages 285–295, Hong

Kong, China.

Zhang, B. and Srihari, S. N. (2003). Binary vector dis-

similarity measures for handwriting identiﬁcation. In

Proc. of SPIE, Document Recognition and Retrieval

X, pages 28–38, Santa Clara, CA, USA.

ICSOFT 2010 - 5th International Conference on Software and Data Technologies

304