NEW PSEUDO NEAR COLLISION ATTACK ON TIGER

Dibyendu Mallik and Debdeep Mukhopadhyay

Department of Computer Science and Engineering, IIT Kharagpur, Kharagpur, India

Keywords:

Hash function, Tiger, Collision attacks, Pseudo collision, Meet in the middle attack.

Abstract:

Tiger is a cryptographic hash function created by Anderson and Biham in 1996 with hash value of 192 bits.

Reduced round variants of Tiger have shown some weaknesses recently. Kelsey and Lucks have shown a

collision attack on Tiger reduced to round 16 and 17. Mendel and Rijmen have found 1 bit pseudo near

collision for full round Tiger. In this article we discover a new key schedule differential for Tiger which leads

to the ﬁnding of message pairs for 1-bit pseudo near collision.

1 INTRODUCTION

Tiger is a cryptographic hash function proposed by

Anderson and Biham in 1996 (Anderson and Biham,

1996). It has a block cipher like construction and op-

erates on 512 bit messages, which serves as the key

in the block cipher mode. In addition, there is a 192

bit Initial Values (IV). The ﬁnal hash value is of 192

bit. There are 24 rounds in the hash function plus an

additional feedforward step at the end. Recent works

show well known hash function families, like MD4

(Rivest, 1990) can be subjected to collision attacks

by the techniques proposed in (Yu and Wang, 2007;

Dobbertin, 1998). However till now no collision at-

tacks on full round Tiger have been discovered.

Tiger has drawn the attention of several re-

searchers around the world and there has been some

interesting works on collision attacks on reduced vari-

ants of the hash function. In FSE 2006 Kelsey

and Lucks presented a collision attack on 16 and 17

rounds of Tiger, out of the total 24 rounds (Kelsey

and Lucks, 2006). The complexity of the attack is

evaluations of the compression function of Tiger.

They also presented a 1 bit pseudo near collision

for a variant of Tiger reduced to 20 rounds with a

complexity of 2

. In Indocrypt 2006 Mendel et

al. presented collision attack on Tiger reduced to

19 rounds(Mendel et al., 2006). In Asiacrypt 2007,

Mendel and Rijmen presented a pseudo collision at-

tack on full round Tiger (Mendel and Rijmen, 2007).

The complexity of the attack was around 2

compu-

tations of the compression function of Tiger.

Contribution. In the present paper, we revisit the

collision problem in Tiger Hash function and present

some new results. We identify a new key schedule dif-

ferential which leads to 1-bit pseudo near collision of

full round Tiger. To ﬁnd key schedule differential we

have ensured that the message differences generated

by the key scheduler, should have large number of ze-

ros at the starting and ﬁnal rounds, to reduce the num-

ber of conditions on the message bits in the ﬁrst and

last round. Hence the key schedule helps in easy ﬁnd-

ing of consistent colliding pairs, which are reported in

the paper.

The organization of the paper is as follows:Section

2 presents a high level description of the Tiger hash

function. The attack strategy is described in section

3. Section 4 details the 1-bit pseudo near collision at-

tack on full round Tiger, while the work is concluded

in section 5.

2 HIGH LEVEL DESCRIPTION

OF TIGER HASH FUNCTION

Tiger has 2 distinct parts: a key schedule and a

state update transformation. A detailed description

of the function can be found in (Anderson and Bi-

ham, 1996). The notations followed in this article are:

⊕ (XOR), ∆

⊕

(XOR difference), ∆ (Modular differ-

ence), + (modulo 2

addition), * (modulo 2

mul-

tiplication), - (modulo 2

substraction), ¬ (bitwise

NOT), I (2

), I

′

), I

′′

427

Mallik D. and Mukhopadhyay D. (2010).

NEW PSEUDO NEAR COLLISION ATTACK ON TIGER.

In Proceedings of the International Conference on Security and Cryptography, pages 427-430

DOI: 10.5220/0002940104270430

 SciTePress

2.1 State Update Transformation

The state update transformation of Tiger starts from

an initial value of three 64 bit words and updates

them in three passes of eight rounds each and after 24

rounds an additional feedforward round is added. For

details of state update transformation see (Anderson

and Biham, 1996)

2.2 Key Schedule

Each round of Tiger uses one message word X

as its

round key. The 512 bit message block is divided into

8 byte message X

, X

which

are used as the keys of the ﬁrst 8 rounds. The remain-

ing 16 rounds key are generated by an invertible op-

eration. The KeySchedule operation modiﬁes its input

in two passes.

3 ATTACK STRATEGY

In this section we brieﬂy discuss the attack strategy

of Kelsey et. al. and Mendel to perform collision

attacks on the Tiger hash function. However it may be

noted that the ﬁnal feedforward step is omitted in both

cases. This attack strategy belongs to a general class

of cryptanalysis as presented in (Kelsey and Lucks,

2006) and (Mendel and Rijmen, 2007). The attack

can be stated as follows:

1. A differential characteristic in the key schedule

which holds with high probability is found. In

ideal case the probability should be 1.

2. Certain message bits are modiﬁed to obtain de-

sired difference value in the Tiger state variables

which can be canceled by the difference in mes-

sage words in the subsequent rounds.

3.1 Finding a Good Differential

Characteristic for Key Schedule of

Tiger

The objective of this step is to ﬁnd key schedules with

certain desirable properties. We ﬁrst observe possible

differences in the state variables for the i

step, which

can be canceled by suitable message differences in

steps i, i + 1 and i + 2. Such possible difference val-

ues are noted in table 1. The cancellation needs to

take place at the ﬁnal round of the hash function. The

objective was that the message difference generated

by the keyscheduler should have a large number of 0s

at the starting and ﬁnal rounds. To ﬁnd such good dif-

ferentials, we linearize the operations in GF(2) and

Table 1: Canceling message and state variable differences.

State Variable Difference Message Difference

∆A

i−1

∆B

i−1

∆C

i−1

∆X

i+2

∆X

i+1

∆X

0 0 I 0 0 I

0 I 0 I 0 0

0 I I I 0 I

I 0 0 0 I 0

I 0 I 0 I I

I I 0 I I 0

I I I I I I

choose those which have a high probability of occur-

rence in the real hash function.

3.2 Message Modiﬁcation by Meet In

The Middle

For any i

step of Tiger let the state variables be de-

noted by A

i−1

, B

i−1

, C

i−1

and the corresponding dif-

ferential pairs by A

∗

i−1

, B

∗

i−1

, C

∗

i−1

. The modular dif-

ference ∆(A

i−1

) = A

∗

i−1

− A

i−1

. Similarly, the other

differences ∆(B

i−1

) and ∆(C

i−1

) are deﬁned. We as-

sume we are given all these values. Then the modular

difference δ = ∆(C

i+1

) (refer ﬁgure 1) can be forced

to any desired value with probability

using birthday

attack. We try all 2

possibilities of B

i+1

[even] to

generate 2

candidates for the ∆(even(B

i+1

)). Then

we use meet in the middle approach to solve the fol-

lowing equation. The algorithm can be stated as fol-

lows.

1. Store the 2

candidates for ∆odd (B

) in a table.

2. For all 2

candidates for ∆even(B

i+1

)

test if ∆odd (B

) exists with: ∆odd (B

) =

(∆even(B

i+1

) + δ)∗ mult

−1

− ∆(B

i−1

)

A CB

even

odd

even

odd

i+1

i−1

Figure 1: Meet in The Middle Attack.

This technique takes some 2

evaluations of each

functions even and odd and 2

units of storage

space. From our assumption, we know the value

of C

i−1

. Fixing the value of X

[even], the value of

[even] gets known. Since the meet-in-the-middle

SECRYPT 2010 - International Conference on Security and Cryptography

428

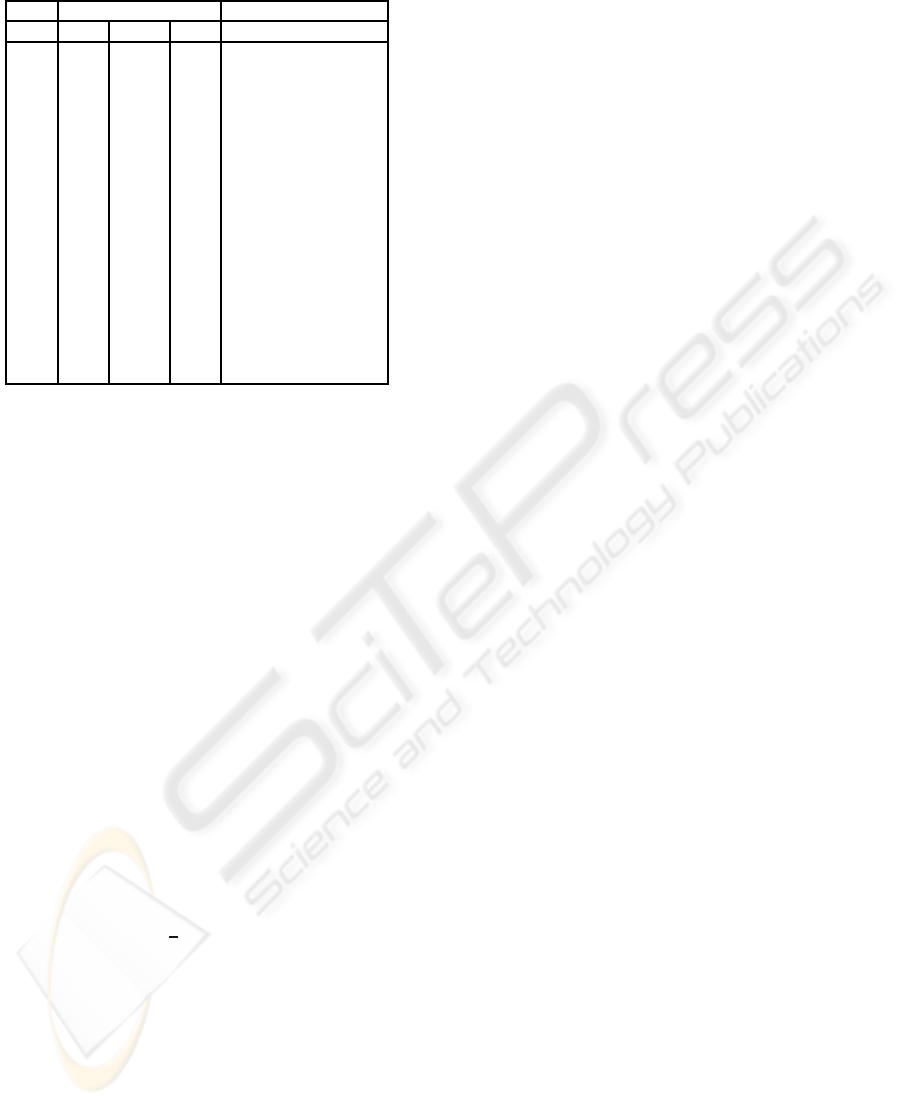
Table 2: Propagation of state variable.

step State Variable Message Difference

i ∆A

∆B

∆C

∆(X

i+1

)

-1 0 0 I I

0 0 0 0 0

1 0 0 0 0

2 0 0 0 0

3 0 0 0 I+I

′

4 * I + I

′

* I

5 * * * I

′′

6 * * * 0

7 * * * I

8 * * * 0

9 * * * I

10 * * K

⊕

11 * K

⊕

12 0 L

I 0

13 0 I 0 0

14 I 0 0 0

15 0 0 I I

attack produces ∆B

i+1

(even) and ∆B

(odd) satisfy-

ing, X

[odd] = C

i−1

[odd] ⊕ B

[odd] and X

i+1

[even] =

[even] ⊕ B

i+1

[even] we are able to compute 64 local

message bits.

4 1-BIT PSEUDO COLLISION ON

FULL ROUND OF TIGER

In this section we present a pseudo near collision of

full round Tiger including the feedforward round but

for different key schedule differential as observed in

(Mendel and Rijmen, 2007). Table 1 shows that mes-

sage differences (∆X

, ∆X

i+1

, ∆X

i+2

) = (I, 0, 0) can be

canceled out by introducing state variable difference

(0, 0, I) at (i − 1)

step. Now introducing message

difference I, 0, 0 at 16, 17, 18

round and setting all

the message differences of the ﬁnal round of Tiger

to 0, we obtain the following key schedule differ-

ential by running the inverse key schedule opera-

tion: (I, 0, 0, 0, I + I

′

, I

′

, I

′′

, 0) → (I, 0, I, 0, 0, 0, 0, 0) →

(I, 0, 0, 0, 0, 0, 0, 0) The key schedule differential

holds with probability

which is quite high and con-

tains four and seven zeroes at the initial and ﬁnal

round respectively. Therefore, this differential fol-

lows the property of good differential as mentioned in

section 4. In order to create collision after 23

round

we have to create a collision after 16

round of Tiger

ie, (∆A

, ∆B

, ∆C

) = (0, 0, 0). Therefore the state

variable difference at 15

round should be (0, 0, I).

Now if we generate state variable difference (0, I, 0)

at 13

round then the difference propagates to 15

round and produces the desired difference. The state

variable propagation is shown in table 2. To create

∆B

= I we have to force ∆C

to I and as ∆A

= 0,

the difference ∆odd(B

) = odd (B

)−odd (B

⊕ I)

should be canceled out by creating its opposite mod-

ular difference L

at B

. In order to create the de-

sired difference ∆B

we force ∆C

to a low weight

Hamming difference L

⊕

(Hamming weight of L

⊕

10 to optimize the complexity of meet in the middle

attack) by message modiﬁcation technique such that

the modular difference L

and the XOR difference L

⊕

are consistent. We use the same deﬁnition of consis-

tency as mentioned in Mendel and Rijmen.(Mendel

and Rijmen, 2007). Let L

′

be the set of all modular

differences L

which are consistent. For the propa-

gation of desired difference from C

to B

the mod-

ular differences should be consistent. Therefore we

construct the set L as follows:

L =



∈ L

′

: L

= odd(B

⊕ I) − odd(B

)



The size of the set L is related to the Hamming weight

of L

⊕

. It is observed from the round structure of

Tiger that to get the desired difference ∆C

= 0,

∆A

should be 0. Therefore from the construction of

Tiger it is observed that the difference ∆odd(B

) =

odd(B

)− odd(B

⊕ L

⊕

) should be canceled out by

introducing an opposite modular difference K

at B

by forcing ∆

⊕

to an XOR difference K

⊕

(of Ham-

ming weight 8) which is consistent to K

. We con-

struct the set K from the set K

′

which is the set of all

consistent modular differences K

as follows:

K =



∈ K

′

: K

= odd(B

⊕ L

⊕

) − odd(B

)



These sets are computed only one time in this attack.

It has complexity of about 2

4.1 Construction of Desired Differences

We have to know ∆A

, ∆B

and ∆C

for the meet-

in-the-middle attack to force ∆C

to K

⊕

. For this

we choose random values for B

and B

and com-

pute A

= (B

+ odd(B

)) ∗ mult, its corresponding

differential A

∗

and ∆C

= ∆even(B

). Since there is

no difference in X

, B

and C

we get ∆(B

) = I + I

′

Choosing random value for B

we can calculate the

vales of all the state variables of step 5. Again choos-

ing arbitrary values for X

, X

and X

we calculate

the values of A

, B

, C

and their corresponding dif-

ferential values A

∗

, B

∗

, C

∗

are also calculated. These

operations ﬁx the message words X

, X

and X

As the values of ∆A

, ∆B

and ∆C

are known

now, desired XOR difference ∆C

, can be con-

structed by using message modiﬁcation technique.

For all modular difference in K

we do a message

modiﬁcation step and check if ∆(C

) = K

⊕

. This ex-

periment holds with probability of 2

−8

, as the Ham-

ming weight of K

⊕

is 8. The message modiﬁcation

NEW PSEUDO NEAR COLLISION ATTACK ON TIGER

429

technique holds with probability

because of Birth-

day Paradox. Therefore, success probability of the

attack is

∗ (2

−8

)∗ |K| =

. This step has complexity

of about 2

computations. This step ﬁxes the mes-

sage words X

[even] and X

[odd].

Choosing some random values for X

[even](and

its corresponding differential pair), ∆A

, ∆B

and ∆C

which are needed for meet in the middle step to force

the value of ∆C

to L

⊕

are calculated. We again

apply message modiﬁcation technique to construct

the target difference. For all modular difference in

we do a message modiﬁcation step and check if

∆(C

) = L

⊕

. This experiment holds with probabil-

ity of 2

−10

, as the Hamming weight of L

⊕

is 10. The

message modiﬁcation technique holds with probabil-

ity

. Therefore, success probability of the attack

∗ (2

−10

) ∗ |L| =

. This step has complexity of

about 2

computations. This step ﬁxes X

[odd] and

[even].

To generate the message difference in 11

round

we again apply a message modiﬁcation techniques.

This step ﬁxes the message word X

[even] and

[odd]. XOR difference and modular difference

by I is interchangeable with probability 1 and the

message modiﬁcation step succeeds with

. There-

fore this step succeeds with probability

and com-

plexity of 2

36.5

evaluation of the compression func-

tion.(Mendel and Rijmen, 2007)

4.2 Constructing the Message Word

The attack ﬁxes the words X

to X

and X

[odd].

To compute the values of the message word X

to X

we choose random value for X

[even].

From our known values we can calculate X

and

from the following equations: X

= (X

−

⊕ X

⊕ (¬(X

+ (X

⊕ (¬X

≫ 23))) ≫

23))) + X

, and X

= (X

⊕ (X

− X

)) − (X

⊕

0123456789ABCDEF) ≫ 23))) + X

. After know-

ing the values of X

. . . X

we run the inverse key

schedule operation of Tiger to compute X

to X

4.3 Constructing the Initial Values of

State Variables

After knowing the values of X

to X

we can run Tiger

rounds in backward direction to get the initial values.

As the valuesof A

, B

, C

are knownwe can calculate

the values of A

−1

, B

−1

, C

−1

by backward propagation.

To cancel out the message differences ∆X

we apply

an initial value difference ∆C

−1

= I.

5 CONCLUSIONS

In this paper we have identiﬁed a new key sched-

ule differential for the Tiger hash function. We have

shown how the key schedule differentials can be ap-

plied to obtain a 1-bit pseudo near collision attack of

complexity of 2

for full round Tiger. Finding of a

new key schedule differential for 1-bit pseudo near

collision attack shows security margins of Tiger is not

as high as it was expected.

REFERENCES

Anderson, R. J. and Biham, E. (1996). Tiger: A fast new

hash function. In Gollmann, D., editor, FSE, volume

1039 of LNCS, pages 89–97. Springer.

Dobbertin, H. (1998). Cryptanalysis of md4. J. Cryptology,

11(4):253–271.

Kelsey, J. and Lucks, S. (2006). Collisions and near-

collisions for reduced-round tiger. In FSE, volume

4047 of LNCS, pages 111–125. Springer.

Mendel, F., Preneel, B., Rijmen, V., Yoshida, H., and

Watanabe, D. (2006). Update on tiger. In IN-

DOCRYPT, pages 63–79.

Mendel, F. and Rijmen, V. (2007). Cryptanalysis of the tiger

hash function. In Kurosawa, K., editor, ASIACRYPT,

volume 4833 of LNCS, pages 536–550. Springer.

Rivest, R. L. (1990). The md4 message digest algorithm. In

Menezes, A. and Vanstone, S. A., editors, CRYPTO,

volume 537 of LNCS, pages 303–311. Springer.

Yu, H. and Wang, X. (2007). Multi-collision attack on

the compression functions of md4 and 3-pass haval.

In Nam, K.-H. and Rhee, G., editors, ICISC, volume

4817 of LNCS, pages 206–226. Springer.

SECRYPT 2010 - International Conference on Security and Cryptography

430