PRIORITY SELECTION FOR MULTI-ROBOTS
S. H. Ji, S. M. Lee and W. H. Shon
Korea Institute of Industrial Technology, Sa-1-dong, Sangrok-gu, Ansan-si, KyungKi-do, South Korea
Keywords: Collision Model, Multi-robots, Mobile-robot Motion Planning, Priority Selection.
Abstract: The priority selecting problem for multi-robots deals with the determination of the relative importance of
multi-robots with the limited capability in speed and acceleration in order that the robots should arrive in the
minimum time without any collision. Unlike the case of a single robot, the arrival time of multi-robots
depends on the delayed action for collision-avoidance. The delayed action time to avoid collision varies
according to the priority order of the robots. This means that faster motion completion can be achieved by
altering the distribution of the priority. However, the priority decision which provides the collision-free
optimum operation of multi-robots cannot be solved mathematically. It is because the collision avoidance
process among robots is closely linked mutually. Therefore in this paper, based on (M,D) network model, in
considering the priority decision, how to reduce the complexity of priority decision is suggested by selecting
the robots which have influence on operating performance of total robots. Conclusively, the effectiveness of
the proposed approach is confirmed through simulation.
1 INTRODUCTION
Multi-robot motion planning is one of the essential
research fields in robotics and has been studied for
the last several decades. Multi-robot motion
planning, however, is still a challenging field of
research, having some technical difficulties in
resolving conflict among agents. Especially, the
centralized approaches to multi-robot motion
planning have been faced with problems such as the
curse of dimensionality, complexity, computational
difficulty, and NP-hard problem (Canny, 1988)
(Akella and Hutchinson, 2002). These problems are
due to the fact that one system alone takes up the
whole burden for planning motions of all agents
interactively.
To overcome these problems in the approach,
some researcher presented computational approach
based on the systematic tools. The multi-robot
motion planning problem is converted to a job
scheduling problem or a constraint satisfaction
problem (Barberl, et. al., 2001) (Chen, et. al., 2001).
The converted problem is solved by project
management tools or priority based tools. We
proposed the extended collision map method which
enables more than three robots to proceed with the
collision-free operation according to the priority by
going on the collision avoidance process one after
another from the highest priority robot (Ji, et. al.,
2007).
Unlike the case of a single robot, the arrival time
of multi-robots depends on the delayed action for
collision-avoidance. The delayed action time to
avoid collision varies according to the priority order
of the robots. This means that faster motion
completion can be achieved by altering the
distribution of the priority. Therefore, this priority
order is a very important design factor of multi-robot
system. But a few researches have attempted to the
problem. Moreover, the researches were based on
the static path information of robots without
considering their mobility (Bennewiz, et. al., 2001).
So, the type of approaches failed to give a
reasonable solution to the priority selection problem
when they were applied to a number of robots.
Therefore, in this paper, we suggest the way how
to select the priority order for collision-free multi-
robot operation considering static path information
and dynamic mobility of multi-robots. For the
purpose of our aim, analysis on characteristics of
collision among agents is needed. Thus, in this paper,
we use (M,D) network model based upon collision
features which can express not only the complicated
mutual interference among more than two robots but
also help us design the collision-free operation of
multi-robots and figure out the operating completion
time of robots (Ji, et. al., 2009). And in this paper,
403
Ji S., Lee S. and Shon W. (2010).
PRIORITY SELECTION FOR MULTI-ROBOTS.
In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 403-408
DOI: 10.5220/0002943604030408
Copyright
c
 SciTePress

based on (M,D) network model, in considering the
priority decision, how to reduce the complexity of
priority decision is suggested by selecting the robots
which have influence on operating performance of
total robots.
The remainder of the paper is organized as
follows: Section 2 briefly describes multi-robots.
Section 3 defines our priority selection problem in a
mathematical form and Section 4 presents the
concept of the key technique of this paper. Section 5
provides an implementation for a number of robots
in order to verify the effectiveness of the proposed
approach and finally this paper is concluded in
Section 6.
2 MULTI-ROBOT SYSTEM
2.1 Assumptions
To reduce complexity of multi-robot motion
planning, the extended collision map method applies
several concepts as follows:
[Global Off-Line Path Planner]
Global off-line path planner (Central planner) can
give the safe paths to all robots. In this paper, ‘safe
path’ is the meaning that no robot will not crossover
any other robot’s starting point or destination if it
keeping on its own safe path. Therefore there can be
intersection points among robots’ paths.
[Agent Model]
Robots in robotics can have either car-like or
human-like shapes. Computation load can be
reduced by using a simple model of a robot, so we
model an agent as a circle. It is expressed by radius r
and a center point in Eq.(1).
)](),([)( tptptp
yx

(1)
A radius of a robot is defined as an extended
value of real shape considering the robot path’s
radius of curve and maximum path deviation error
for stability. In real applications, there are sensor
noise and jittering in sampling control interval. And
there are effect on motion accuracy of slip and slope.
[Motion Characteristics of Agent]
An agent has physical constraints-velocity and
acceleration limitation denoted by Eq. (2).
maxmax
|)(|,|)(| atpvtp 

(2)
A robot was assumed to always move in full
speed within physical constraints and have a
trapezoid model of the velocity profile. This
assumption simplifies motion planning, because the
central planner only has to consider the speed down
for collision avoidance. All of the collision-free
strategies in extended collision map are based on
this assumption.
2.2 Collision-model
We suggested the collision model which express
collision relations and predict possibility of
collisions among the robots (Ji, et. al., 2009). And
all of the robot’s minimum delayed departure time
for collision-free navigation can be extracted from
the model. The elements of collision model are
defined in Table 1.
Table 1: Elements of collision model.
Symbols
Meaning
V Node space(V) = { 1, …, N}.
This is a set of agent identified numbers.
E
Link space(E) = { (i, j, k) ∈ V
2
x N | i ∈
P
+
j
, k=1,…, k(i,j) }.
This is a set of collision regions among
agents.
P
+
j
is explained in priority order space, and
the links go from the agent with higher
priority to the other agent.
k(i,j) is the number of collision regions
between agent j and agent i . So some agent
can have more than two links with other
agent if they have several collision regions
C
Link relation space(C) = { (M
ij
k
, D
ij
k
) ∈ R
2
| (i,j,k) ∈ E }.
This is a set of collision characteristics, M
and D in the Table I.
T
Node navigation characteristic space(T) =
{ (T
i
delayed
, T
i
traveled
) ∈ R
2
}.
This is a set of agents’ delayed departure
times and pure traveled time from the start
point to the destination.
P
Priority order space(P) = {(N
1
, …, N
N
) ∈
V
N
| N
i
is the identified number of the agent
with the i
th
highest priority}
This is a set of agent orders in which each
agents are placed from an agent with the
highest priority to an agent with the lowest
priority.
P
+
j
is the set of agents which have higher
priorities than agent j in P and P
-
j
is the set
of agents which have lower priorities than
agent j in P, the space of priority order space
Now, we express the collision model from the
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
404

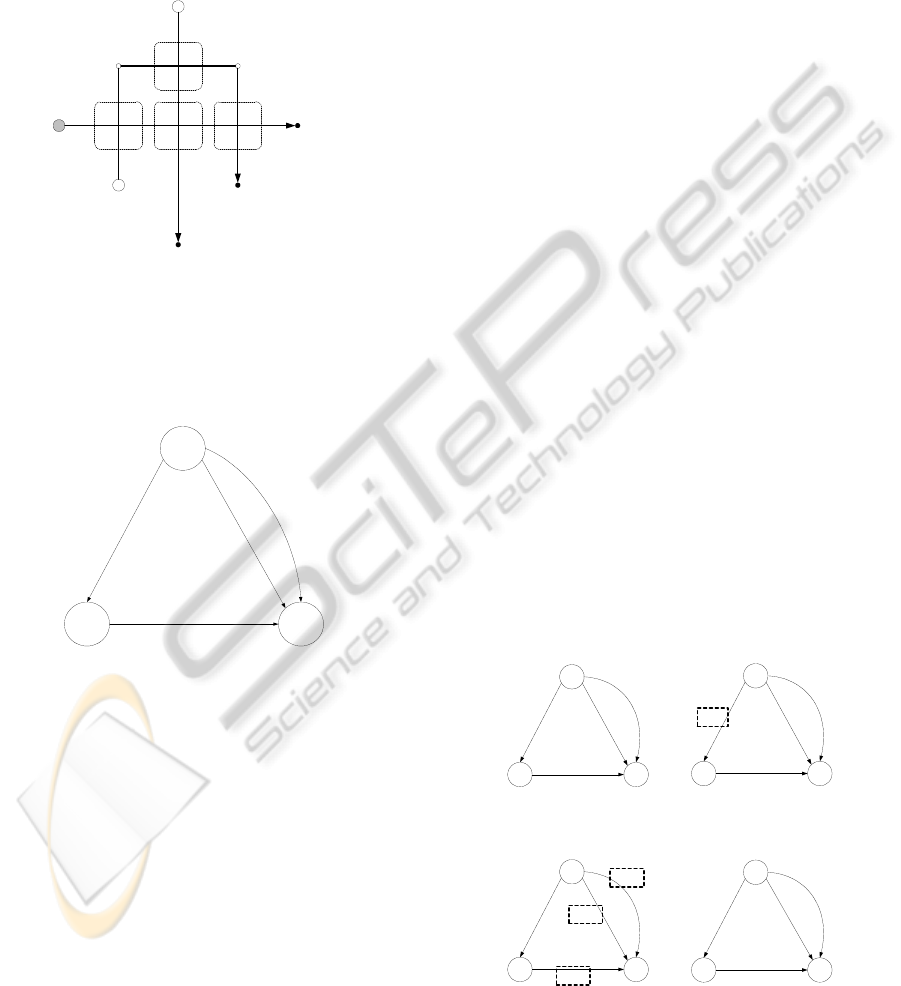
case in Fig. 1 as the network model shown in Fig. 2.
There are three robots (agent 1, 2, and 3) with path
shapes as shown in Fig.1. We assume that all of
agent’s radii are 5m and there velocities are 1m/sec,
2m/sec, and 1m/sec. We assume also that it takes no
time for them to accelerate, decelerate, or turn
around. And we assume their priority order is 1-2-3.
agent 1
path of agent 1 : P1 - P4
path of agent 2 : P2 - P5
p
ath of a
g
ent 3 : P3 - P6 - P7 - P8
I
31
1
A
1
A
3
A
2
agent 2
agent 3
P
1
(0,50)
P
3
(25,25)
P
4
(100,50)
P
2
(50,100)
P
5
(50,0)
P
7
(75,75)P
6
(25,75)
P
8
(75,25)
I
21
1
I
31
2
I
32
1
scale : ( m, m )
Figure 1: Three agents with intersection points.
The collision network model is as followed: V =
{1,2,3}, P=(1,2,3), E={(2,1,1), (3,1,1), (3,1,2),
(3,2,1)}. C and T are shown in Fig. 2.
A1
A2 A3
M
21
1
, D
21
1
M
31
1
, D
31
1
M
31
2
, D
31
2
M
32
1
, D
32
1
{T
1
delayed
, T
1
travelded
}
{T
2
delayed
, T
2
travelded
}{T
3
delayed
, T
3
travelded
}
Figure 2: Collision model for three agents in Figure1.
2.3 Collision-free Motion Planner
based on Collision Model
2.3.1 Collision-free Motion Planner for a
Robot on Collision Model
When a robot (A
i
) is delayed by T
i
d
, the collision
characteristics related to the robot in the model are
affected. For inlet links from the higher priority
robots, M’s increase and D’s decrease by delayed
departure time (T
i
d
). In the other, for outlet links to
lower priority robots, M’s decrease and D’s increase
by the same amount. And as a result of the time
delay, the safe inlet link may be dangerous. So we
proposed an iterative approach to find the minimum
delayed departure time for collision avoidance as
followed:
Step1: Extract the links on which the robot is
expected to collide with higher priority robots (Inlet
Links) by use of collision characteristics.
Step2: Define an instantaneous delayed departure
time (T
i
d
) as the maximum of the Ds’ in the selected
links.
T
i
d
= max ( {D
ij
k
| j ∈ P+(i), (i, j, k)∈E
s.t. M
i
j
k
> 0 and D
i
j
k
> 0})
(3)
Step3: Modify node and link parameters by T
i
d
.
Step4: Without dangerous inlet links to the robot,
the robot can go to its destination safely. Otherwise,
Execute above actions from the first stage.
2.3.2 Collision-free Motion Planner for
Multi- robot on Collision Model
Step1: Select a robot from the priority order space
(P) by use of priority index.
Step2: if the robot has the highest priority, go to first
stage. Otherwise, apply the collision-free motion
planner on collision model to the robot so that the
robot can navigate safely.
Step3: if the selected robot has the lowest priority,
all of the robots can navigate safely, and finish up
this algorithm. Otherwise, increase priority index by
1 and go to first stage.
Te procedure of this algorithm for the three
robots in Fig. 1 is shown in Fig. 3. Because all
robots’ links is in a safe state in Fig. 3(d), we can
predict that the robots can navigate without collision
among them.
A1
A2 A3
{40,0}
{30, 0}
{30, 0}
{35, -5}
{0, 100}
{20,100} {27.5, 7
5
A1
A2 A3
{40,0}
{2.5, 27.5}
{2.5, 27.5}
{7.5, 22.5}
{0, 100}
{20,100} {0, 75}
A1
A2 A3
{20 , 20}
{2.5, 27.5}
{2.5, 27.5}
{27.5, 2.5}
{0, 100}
{0, 100} {0, 75}
A1
A2 A3
{20 , 20}
{2.5, 27.5}
{2.5, 27.5}
{27.5, 2.5}
{0, 100}
{0, 100} {0, 75}
(a)
(b)
(c)
(d)
Figure 3: Procedure of collision-free motion planner on
collision model for the agents in Figure 1.
PRIORITY SELECTION FOR MULTI-ROBOTS
405

3 PRIORITY SELECTION
PROBLEM
The priority selecting problem deals with the
determination of the priorities of multi-robots with
the limited capability in speed and acceleration in
order that the robots should arrive in the minimum
time without any collision. In this paper, we express
the problem as shown in Eq.(4) using (M,D)
network model.
Objective : Minimize J = max(T
1
completed
,
…, T
N
completed
)
Constraints : M
i,j
k
* D
i,j
k
≤ 0, ∀(i,j,k)∈ E
(4)
Where, T
i
completed
is the arriving time of robot i which
is the sum of T
i
delayed
and T
i
traveled
. M
i,j
k
*and D
i,j
k
are
the collision characteristics of the k
th
collision region
between robot i and robot j.
T
i
traveled
is affected by path information and
mobility of only robot i. But T
i
delayed
is determined
according to priority order of the robots and
relations with other robots which is expressed with P,
E, and C on the (M,D) network model.
In this paper, we redefine the priority selection
problem for N robots based on (M,D) network as a
Traveling Salesman Problem(TSP). We define
robots and connections between neighbors in a
priority order list as arcs as nodes and arcs on the
network model. And we add a zero node to the
model in order to convert our priority selection
problem to a TSP. We define costs of arcs on the
network model as shown in Eq(5).
C
0i
= T
i
travele
d
, C
i0
= 0 for all agent i
C
i
j
= max[ 0, T
j
completed
- T
i
completed
]
(5)
Once robots’ motion profiles are planned and
robots’ priorities are determined, we can get a
primitive (M,D) network model, G = {V,E,C,T,P}
and apply our collision-free motion planning
algorithm to the robots . As a result of this motion
adaption, we obtain the values of C and T defined on
the table 1. These actions proceeds according to our
predefined procedures suggested in section 2.3 and
its calculation time is defined as a polynomial
equation of the number of robots.
Because T
i
completed
has T
i
delayed
which is affected
by the position of robot i in a priority list, the cost
between robot i and robot j, C
ij
, varies according to
the positions in the lists. So, our priority selection
problem is a dynamic asymmetric problem.
4 SOLUTION TO THE PROBLEM
A TSP is known as a NP-hard problem. So, it is
difficult to solve the problem mathematically. Thus,
in this paper, we suggest how to cut out less
important robots in the meaning that they will not
affect the completion time of whole robots and
reduce the volume of search space. In order to cut
down search space, we use a method, BL-EDF
(Bottom level Earliest Deadline First) scheduler,
which is a task planner for multi-tasks with common
resources.
4.1 BL-EDF Scheduler
The objective function of multi-tasks with priorities
operating on M CPU’s is defined in Eq. (6). To
overcome the drawbacks of the centralized approach,
the extended collision map method applies several
concepts as follows:
Objective : Maximize J = min(S
1
, …, S
N
)
S
i
= E
i
– T
i
completed
T
i
completed
= T
i
worked
+ T
i
delayed
Constraints : More two tasks should not
operate on a CPU at the same
time
(6)
Where, N is the number of robots and E
i
and S
i
are the deadline time and slack time of robot i.
The BL-EDF scheduler applied to our priority
selection problem is as shown in table 2.
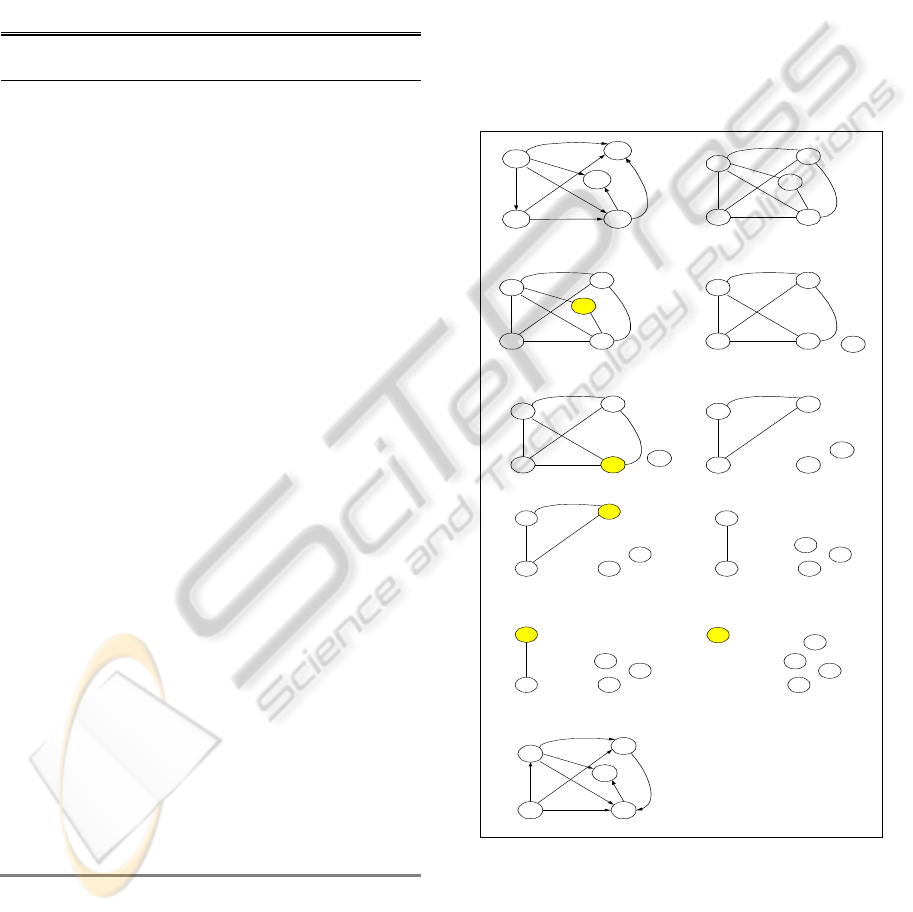
For example, there are 4 tasks in urgent group as
shown in Fig. 4. For all tasks, delay times which are
caused by tasks in urgent group and slack time are
calculated. And if all slack times of a task are
positive, the task is moved to less important task
group. The procedure continues until there is no task
in urgent group of which slack times are positive.
A1
A2
A3
A4
A1
A2
A3
A4
A4
A1
A3
Urgent Group
Group (1)
Group (1)
Group (2)
A2A4
A1
A3
Group (1)
Group (2)
Urgent Group
IterNum = 0
IterNum = 1
IterNum = 2 IterNum = 3
Unchanged
Negtative Slack Time
Positive Slack TIme
Urgent Group
Urgent Group
Lower
Higher
Figure 4: Procedure of BL-EDF scheduler.
4.2 Reduction of Search Space
The priority selection problem for multi-robot
motion is converted to the priority selection problem
for multi-task execution by defining deadline time of
tasks(E
i
), and tasks execution times (T
i
worked
) in
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
406

Eq.(6) as the maximum of robot traveled
times(max[ T
1
traveled
, …, T
N
traveled
]) and traveling
times of robots(T
i
traveled
) in Eq.(4). And a robot’s
maximum delayed time is equal to a sum of all M’s
and D’s of collision regions related to the robot.
Therefore, task’s delayed time in redefined multi-
task priority selection problem is determined with a
sum of all M’s and D’s of inlet link to the robots as
shown in Eq. (7).
Table 2: BL-EDF scheduler.
Procedure
Step 1 <Initialization>
1.1
Assign all Tasks to Urgent Group(UG), IterNum ← 1,
UGN ← N, k ← 0
Calculate T
i
worked
of all Tasks (i=1 to UGN )
Step 2 <Detecting Not Urgent Tasks >
For all tasks in UG (i=1 to UGN) Do
2.1 Determine T
i
delayed
by sum of possible delayed
time for tasks in UG
2.2 Calculate T
i
completed
and S
i
2.3 Classify Tasks by signs of S
i
If S
i
> 0, Then move task i to N(I) and increase k by
1
End of Loop – i
2.4 If k=0 or UGN = 1, Then Go to Step 3,
Else UGN ← UGN – k , k←0, increase IterNum by 1
and Go to Step 2
Step 3 <Assign priority of All Tasks>
For k=1 to IterNum Do
3.1 Assign lowest priority to Tasks in N(k), Task
order in an N(k) is not important
End of Loop – k
3.2 Examine all the priority order for Tasks in UG
which maximize J
If J is negative, Then return FALSE
Else Assign this priority order upper tasks in
N(IterNum)
Complete scheduling
T
i
delaye
d
=∑
j
∑
k
(M
ij
k
+ D
ij
k
) where j∈P
i
+
(7)
The procedure of BL-EDF scheduler for 5 robots
is shown in Fig. 5. The (M,D) network of the robots
with priority order {1-2-3-4-5} is shown in Fig. 5(a).
In Fig. 5(b), links has no direction and its value is
equal to a sum of M and D in order to apply BL-
EDF scheduler to the robots. In Fig. 5(c), robots’
maximum completed time and slack time are
calculated. In Fig. 5(c), because robot 4 (A4) has a
positive value, robot 4 can be removed from urgent
group. The (M,D) network model of remain robots
without robot 4 is shown in Fig. 5(d) where robot 3
has a positive slack time. Therefore, robot 5 moves
from urgent group to a less important group. This
procedure iterates until there is no change in urgent
group or there is one robot in the group as shown in
Fig. 5(j). Finally, we get priority order {2-1-5-3-4}
and its (M,D) network model is as shown in Fig.
5(k).
{8,3}
{-4,12}
{3,1}
{0,34}
{0,55}
{6,3}
{5,2}
{5,8} {7,1}
{0,32}
{3,4}
{0,40}
{0,35}
A1
A2
A5
A4
A3
11
8
4
34
55
9
7
13
8
32
7
40
35
A1
A2
A5
A4
A3
11
8
4
74/-19
80/-25
9
7
13
8
56/-1
7
59/-4
53/2
A1
A2
A5
A4
A3
8
4
34
55
9
13
8
32
7
40
A1
A2
A5
A4
A3
8
4
63/-8
80/-25
9
7
13
8
49/6
7
59/-4
A1
A2
A5
A4
A3
4
34
55
13
7
40
A1
A2
A5
A4
A3
(a)
(b)
(c)
(d)
(e)
(f)
55
A1
A2
A5
A4
A3
{8,3}
{-4,12}
{3,1}
{0,34}
{0,55}
{6,3}
{5,2}
{8,5}
{1,8}
{0,32}
{3,4}
{0,40}
{0,35}
A1
A2
A5
A4
A3
4
56/-1
72/-17
13
7
51/4
A1
A2
A5
A4
A3
34
55
13
A1
A2
A5
A4
A3
47/8
68/-13
13
A1
A2
A5
A4
A3
(g)
(h)
(i)
(j)
(k)
Figure 5: Application of BL-EDF scheduler for multi-
robots.
5 SIMULATION RESULTS
In our simulation, robots were modeled circles of
PRIORITY SELECTION FOR MULTI-ROBOTS
407

which radius, speed is 0.5 [m] and 1[m/sec] each.
Their speed model was assumed to be instantaneous
such that it took no time for them to accelerate from
stationary status to full speed. And the robots were
located uniformly in a square with 100[m] side
length. We assumed that robots’ paths were
Manhattan city typed paths. And we assumed that
their traveled times and sums of collision
characteristics, M and D, were distributed uniformly
in [40, 80] and [4, 20] each. Finally, we assumed
delayed times (D’s) of collision regions were
distributed uniformly in [-8, 8].
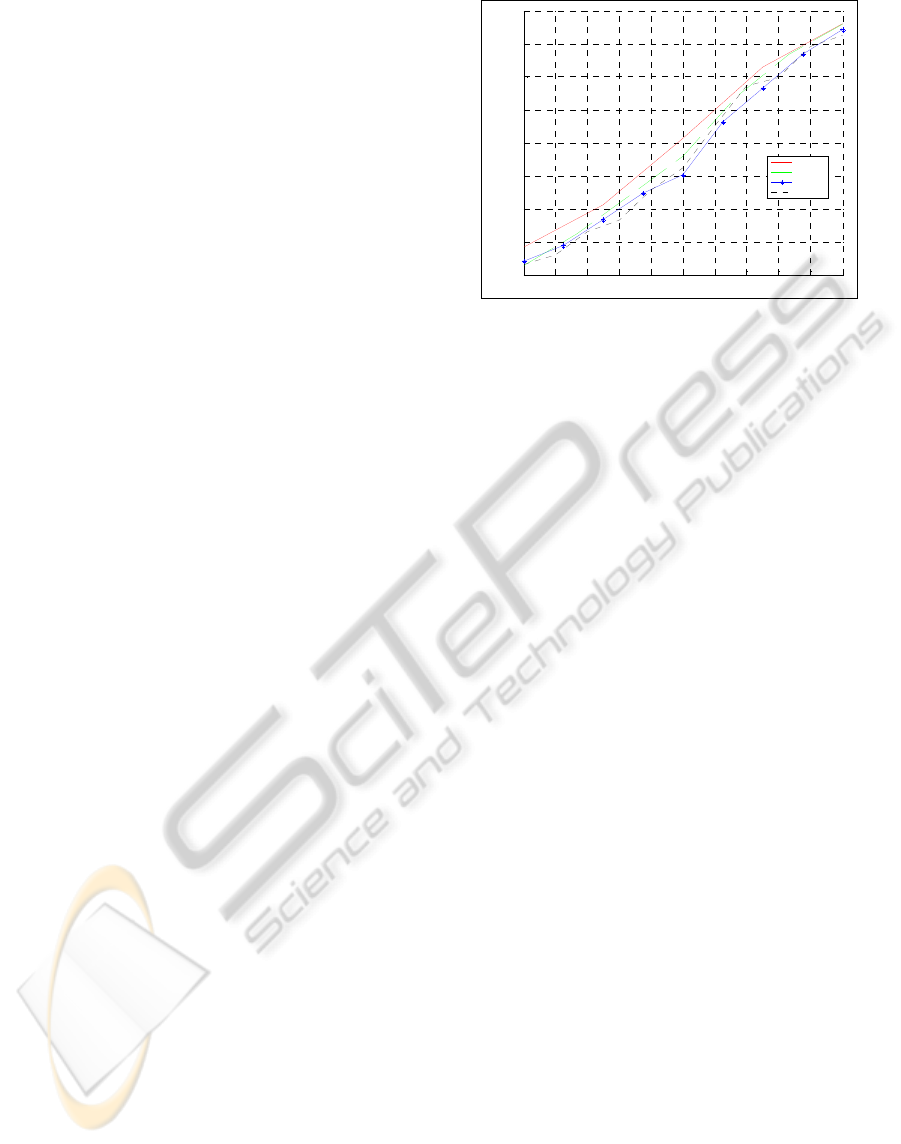
We did 100 simulations for the 20, 30, 40, and
50 robots with 3 times intersections as many as the
numbers of robots. In the Fig. 6, the x-axis shows
the ratios of the numbers of intersections to the
numbers of robots. This variable expresses the mean
of the number of intersections which each robot has
with other robots and is related to of environments.
And the y-axis shows the ratios of the numbers of
robots in final urgent group to the numbers of robots.
This variable expresses effectiveness of BL-EDF.
Regardless of the number of robots, when
normalized numbers of intersections are around 2,
normalized numbers of robots in final urgent group
are about 0.5. Therefore, we expect that our BL-EDF
may reduce 50% in the number of robots in urgent
group. In some applications including social security
field, it is reasonable to assume 12 – 14 robots of
which normalized number of intersections is 2.
Therefore we expect that our algorithm suggested in
this paper cut down calculation time needed to
determine priority orders of multi-robots to 0.01 %
of original expected one.
6 CONCLUSIONS
In this paper, we converted a priority selection
problem for multi-robots with collision-model based
motion planner to a priority selection problem for
multi-tasks with common resources. And we showed
that this problem is a TSP. Thus, we applied BL-
EDF for multi-tasks to our priority selection problem
in order to cut down search space. And effectiveness
of our algorithm in this paper was proved with
simulation results. In future, advance in information
technologies and communications is expected to
help the proposed approach be more practical in
social security applications.
1 1.2 1.4 1.6 1.8 2 2.2 2.4 2.6 2.8 3
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
Normalized number of Intersections
Normalized number of Robots
in final urgent group
20 Robots
30 Robots
40 Robots
50 Robots
Figure 6: Results of BL-EDF scheduler for multi-robots.
ACKNOWLEDGEMENTS
This work was supported by the Program from the
Ministry of Knowledge Economy (MKE).
REFERENCES
J. F. Canny, 1988. The Complexity of Robot Motion
Planning, MIT Press.
S. Akella and S. Hutchinson, 2002. Coordinating the
Motions of Multiple Robots with Specified
Trajectories,
K. S. Barber, T.H. Liu, and S. Ramaswamy, 2001. Conflict
Detection During Plan Integration for Multi-Agent
Systems, IEEE Transactions on Systems, Man, and
Cybernetics, vol. 31, no. 4, pp. 616-627.
Haoxum Chen, Luh P.B., and Lei Fang, 2001. A Time
Window Based Approach for Job Scheduling, Proc. of
IEEE Int. Conf. on Robotics and Automation.
S. H. Ji, J.S. Choi, and B.H. Lee, 2007. A Computational
Interactive Approach to Multi-agent Motion Planning,
International Journal of Control, Automation, and
Systems, vol. 5, no. 3, pp. 295-306.
M. Bennewiz, W. Bufgard, and S. Thurn, 2001,
Optimizing Schedules for Prioritized Path Planning of
Multi-Robot Systems, Proc. of IEEE Int. Conf. On
Robotics and Automation.
S. H. Ji, et. Al., 2009, Collision-Model Based Motion
Planner for Multi-Agents in a Factory, Proc. of 6
th Int.
Conf. on Informatics in Control, Automation and
Robotics, pp.378-386.
J. Park, M. Ryu, and S. Hong, 2003, Fair Real-Time
Resource Allocation for Internet End System’s Qos
Support, Lecture Notes in Computer Science, vol.
2713, pp. 764-789.
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
408