REMOTE CONTROL OF A MOBILE ROBOT SUBJECT TO A

COMMUNICATION DELAY

A. Alvarez-Aguirre, H. Nijmeijer

Department of Mechanical Engineering, Eindhoven University of Technology

P.O Box 513, 5600 MB Eindhoven, The Netherlands

T. Oguchi, K. Kojima

Department of Mechanical Engineering, Tokyo Metropolitan University

1-1, Minami-osawa, Hachioji-shi, Tokyo 192-0397 Japan

Keywords:

Mobile robotics, Remote control, Time-delay systems, Controlled synchronization, Nonlinear predictor.

Abstract:

This paper addresses the remote tracking control of a mobile robot subject to a bilateral time-delay. The delay

affects the system since the controller and the robot are linked via a delay inducing communication channel,

such as the Internet, and consequently, the performance and stability of the system are compromised. Based on

the notion of anticipating synchronization, a state estimator which stabilizes the system when it is affected by

a bilateral time-delay is proposed. A stability analysis including the system, tracking controller and estimator

is provided, and the applicability of the proposed delay compensation strategy is demonstrated by means of

experiments between multi-robot platforms located in Eindhoven, The Netherlands and Tokyo, Japan.

1 INTRODUCTION

In the increasingly fast and diverse technological

developments of the last decades the duties and tasks

conferred to control systems have become much more

complex and decisive. Requirements now encompass

ﬂexibility, robustness, ubiquity, transparency and

balancing tradeoffs, among others.

Speciﬁcally, the study of systems embedded with

time-delays and the control methodologies that can

be applied to them has become signiﬁcatively im-

portant as a way to undertake remote, dangerous or

distributed tasks. As a matter of fact, the remote

control, or the control of a system subject to a bilateral

time-delay, is part of the underlying problem in two

of control engineering’s fundamental topics, namely

teleoperation strategies and Networked Control Sys-

tems (NCS). The problem remains a central issue even

though there are many more considerations in addi-

tion to this problem when considering teleoperated

systems and NCS. Examples of aspects to consider

would be transparency and force reﬂection in teleop-

eration (Niemeyer et al., 2008); and varying trans-

mission delays and sampling/transmission intervals,

packet loss, communication constraints and quantiza-

tion effects in NCS (Heemels et al., 2010).

Several techniques have been proposed so far in

order to cope with bilateral time-delay in this setting,

e.g. the use of the scattering transformation, wave

variables formulation, and queuing methodologies to

name a few. A detailed description of such techniques

and many others, together with further references, can

be found in (Hokayem and Spong, 2006) and (Tip-

suwan and Chow, 2003).

In this work, a control strategy which allows the

remote control of a unicycle-type mobile robot is

proposed. The bilateral time-delay is compensated

by means of a state estimator inspired on a predictor

based on synchronization presented in (Oguchi and

Nijmeijer, 2005a) and (Oguchi and Nijmeijer, 2005b).

The main idea behind the state estimator is to re-

produce the system’s behavior without time-delay in

order to drive an anticipating controller. The problem

presents various challenges since the system is non-

linear and subject to a non-holonomic constraint. Ad-

ditionally, the difﬁculties faced when implementing

the ideas proposed in an experimental setting using

the Internet as the communication channel should be

taken into account and are also discussed in depth. In

(Kojima et al., 2010) a similar state estimator has been

Alvarez-Aguirre A., Nijmeijer H., Oguchi T. and Kojima K. (2010).

REMOTE CONTROL OF A MOBILE ROBOT SUBJECT TO A COMMUNICATION DELAY.

In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 55-62

DOI: 10.5220/0002943700550062

 SciTePress

applied to a mobile robot subject to a communication

delay, and the necessary conditions for the estimator’s

convergence have been derived. In this paper an alter-

native approach is taken in order to prove the stability

of the whole system, including the mobile robot, the

tracking controller and the state estimator.

The paper is organized as follows. Section 2

recalls the tracking control of a delay-free mobile

robot. In Section 3, a control scheme intended to

control a mobile robot subject to a bilateral time-

delay is proposed together with its corresponding

stability analysis. Section 4 provides an overview of

the experimental platform used to validate the control

strategies proposed, explains how the most critical

implementation issues were addressed, and presents

the experimental results. Conclusions and ideas for

future work are provided in Section 5.

2 CONTROL OF A UNICYCLE

The tracking control of a unicycle-type mobile robot

is presented in this section. To begin with, consider

the posture kinematic model of a unicycle,

˙x(t) = v(t) cosθ(t),

˙y(t) = v(t) sinθ(t), (1)

θ(t) = ω(t),

in which x(t) and y(t) denote the robot’s position in

the global coordinate frame X-Y , θ(t) deﬁnes its ori-

entation w.r.t to the X axis, and v(t) and ω(t) de-

scribe the robots’ translational and rotational veloci-

ties respectively, regarded as its control inputs. The

system’s state is deﬁned as q(t) = [x(t) y(t) θ(t)]

and the non-slip condition on the unicycle’s wheels

impose a non-holonomic constraint (Brockett, 1983).

The control objective for the robot is to track the

reference trajectory generated by the exosystem,

˙x

(t) = v

(t)cos θ

(t),

˙y

(t) = v

(t)sin θ

(t), (2)

(t) = ω

(t),

with state q

(t) = [x

(t) y

(t) θ

(t)]

. The exosys-

tem’s reference velocities v

(t) and ω

(t) are deﬁned

in terms of its Cartesian velocities ˙x

(t), ˙y

(t) and

accelerations ¨x

(t), ¨y

(t), i.e.,

(t) =

˙x

(t) + ˙y

(t),

(t) =

˙x

(t)¨y

(t) − ¨x

(t)˙y

(t)

˙x

(t) + ˙y

(t)

(3)

The difference between the exosystem’s and the

system’s states may be expressed w.r.t the system’s

“ﬁg˙qe˙temp” — 2010/3/29 — 22:47 — page 1 — #1

′

Figure 1: Mobile robot, reference exosystem, and error co-

ordinates.

local coordinate frame X

–Y

in order to deﬁne the

error coordinates q

(t) = [x

(t) y

(t) θ

(t)]

, as

proposed by (Kanayama et al., 1990) and shown in

Figure (1). These coordinates are given by the clock-

wise rotation of the position differences between q

(t)

and q(t), resulting in,







(t)













cosθ(t) sinθ(t) 0

−sinθ(t) cosθ(t) 0

0 0 1













(t) − x(t)

(t) − y(t)

(t) − θ(t)







(4)

Differentiating (4) w.r.t. time yields the following

error dynamics,

˙x

(t) = ω(t)y

(t) + v

(t)cos θ

(t) − v(t),

˙y

(t) = −ω(t)x

(t) + v

(t)sin θ

(t), (5)

(t) = ω

(t) − ω(t).

A tracking controller which results in closed-loop

error dynamics which have a cascaded structure has

been proposed in (Jakubiak et al., 2002), (Panteley

et al., 1998), and is given by,

v(t) = v

(t) + c

(t) − c

(t)y

(t),

ω(t) = ω

(t) + c

sinθ

(t),

(6)

with c

, c

> 0 and c

> −1 ensuring stability.

3 BILATERAL TIME-DELAY

COMPENSATION

In this section, a state estimator with a predictor-like

structure similar to the one proposed in (Kojima et al.,

2010) is applied to a unicycle-type mobile robot sub-

ject to a bilateral time-delay. The origin of this type

of predictor can be traced back to the appearance of

the notion of anticipating synchronization in coupled

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

“ﬁg˙pred˙bi˙temp” — 2010/2/3 — 0:52 — page 1 — #1

Forward

time-delay

model

Communication

channel

Reference

Trajectory

Controller

Mobile

Robot

State

Predictor

Correcting

Term

Forward

time-delay

Backward

time-delay

Backward

time-delay

model

Figure 2: Bilateral time-delay compensation scheme block

diagram representation.

chaotic systems, which was ﬁrst observed by (Voss,

2000). After the same behavior was observed in cer-

tain physical systems such as speciﬁc electronic cir-

cuits and lasers, it was studied for more general sys-

tems in (Oguchi and Nijmeijer, 2006). As a result

of this generalization, a state predictor based on syn-

chronization for nonlinear systems with input time-

delay was proposed in (Oguchi and Nijmeijer, 2005a).

The same concept, which can be seen as a state esti-

mator with a predictor-like structure, is proposed for

a mobile robot subject to a bilateral time-delay in the

block diagram in Figure 2.

3.1 Controller Structure

When considering a bilateral time-delay the system’s

output is also delayed. In this case the mobile robot is

subject to a forward τ

and backward τ

time-delay,

as denoted in (Hokayem and Spong, 2006). Given

the mobile robot (1) subject to a bilateral time-delay,

the robot’s posture kinematic model after the forward

delay is given by,

˙x(t) = v(t − τ

)cosθ(t),

˙y(t) = v(t − τ

)sinθ(t), (7)

θ(t) = ω(t − τ

From the controller’s side point of view, the robot’s

kinematic model is also affected by the backward

time-delay τ

, resulting in the following model,

˙x(t − τ

) = v(t − τ

− τ

)cosθ(t − τ

˙y(t − τ

) = v(t − τ

− τ

)sinθ(t − τ

), (8)

θ(t − τ

) = ω(t − τ

− τ

To improve the robot’s performance when subject

to the time-delay, the dynamics of the estimator, with

state z(t) = [z

(t) z

(t)]

, are proposed as,

˙z

(t) = v(t)cosz

(t) + ν

(t),

˙z

(t) = v(t)sinz

(t) + ν

(t), (9)

˙z

(t) = ω(t) + ν

(t),

with ν(t) = [ν

(t) ν

(t)]

deﬁning a correcting

term relating the estimator’s and the system’s states.

The correcting term ν(t) is intended to bring the

estimator’s and the system’s states closer, since the

robot’s initial conditions are assumed to be unknown.

There is complete freedom in the design of this term,

with the simplest choice being,

(t) = −K

(t −

−

) − x(t −

)),

(t) = −K

(t −

−

) − y(t −

)), (10)

(t) = −K

(t −

−

) − θ(t −

)),

where

and

model the robot’s forward and back-

ward delays. Hereinafter the forward and backward

time-delays are assumed to be equal and constant, i.e.

= τ

= τ, and modeled perfectly, i.e.

= τ.

The feasibility of this assumption will be discussed

before the experimental results are presented.

In order to ease the computations in the stability

analysis, a different correcting term will be proposed.

Two new sets of error coordinates are deﬁned, namely

(t) and p

(t). The ﬁrst coordinates relate the esti-

mator’s state with the reference trajectory, i.e.







(t)













cosz

(t) sinz

(t) 0

−sin z

(t) cosz

(t) 0

0 0 1













(t) −z

(t)

(t) −z

(t)

(t) −z

(t)







(11)

while the second set relates the delayed estimator’s

state with the current system’s state, i.e.,







(t)













0 0 1













x(t − τ) − z

(t − 2τ)

y(t − τ) − z

(t − 2τ)

θ(t − τ) − z

(t − 2τ)







(12)

where p

= p

= cos z

(t − 2τ) and p

= −p

sinz

(t − 2τ).

Given the error coordinates (11) and (12), the

following correcting term is proposed,

(t) = −K

(t)cos z

(t) + K

(t)sin z

(t),

(t) = −K

(t)sin z

(t) − K

(t)cos z

(t),

(t) = −K

sin p

(t).

(13)

Since the control scheme of Figure 2 uses the

state estimator’s output as the controller’s input, a new

control law is proposed based on the tracking control

(6),

v(t) = v

(t) + c

(t) − c

(t)z

(t),

ω(t) = ω

(t) + c

sinz

(t).

(14)

REMOTE CONTROL OF A MOBILE ROBOT SUBJECT TO A COMMUNICATION DELAY

Remark 1. Due to the input time-delay, the system’s

control action is given by the delayed controller, i.e.,

v(t − τ) = v

(t − τ) +c

(t − τ) −c

(t − τ)z

(t − τ),

ω(t − τ) = ω

(t − τ) +c

sinz

(t − τ).

The resulting control action provides an idea of how

the system will behave. Intuitively, the robot will track

the reference trajectory after a time τ. This will be

examined in detail during the stability analysis.

Remark 2. Although the stability analysis is unique

for each control law, the delay compensation scheme

is controller independent, so in this sense the gener-

ality of the scheme holds. Consider for example a

controller which accounts for actuator saturation and

collision avoidance such as in (Kostic et al., 2009).

3.2 Stability Analysis

In order to describe the system’s performance it

becomes necessary to establish stability criteria. The

system’s control objectives are deﬁned as follows,

• q(t) → q

(t − τ), the system converges to a de-

layed version of the reference trajectory;

• z(t) → q(t + τ), the state estimator anticipates the

system;

• z(t) → q

(t), the state estimator converges to the

reference trajectory.

Considering the control objectives and Remark 1,

the following proposition is formulated.

Proposition 1. Given the unicycle-type mobile robot

(7) subject to a bilateral delay 2τ, the state estimator

(9)-(13), and the control law (14), the robot will track

a delayed version q

(t − τ) of the reference trajectory.

In accordance to Proposition 1 it follows that

proving that the equilibrium point (z

(t), p

(t)) = 0

is stable satisﬁes the control objectives.

The error coordinates (11)-(12) are grouped and

differentiated w.r.t time, and the tracking control

law (14) is substituted in them. Given ξ

]

and ξ

= [z

]

, the result-

ing closed-loop error dynamics are rearranged in the

following cascaded form,

(t) = A

(t,t − 2τ)ξ

(t) + A

(t − 2τ) (15)

+ g(t,t − 2τ, ξ

(t), ξ

(t − 2τ), ξ

(t − 2τ)),

(t) = f

(t, ξ

(t), ξ

(t − 2τ)), (16)

where,

(t,t − 2τ) =







−c

0 0 K

0 0 0 f

0 0 f













0 0 0 0

0 0 K

0 0 0 K







g(t,t − 2τ, ξ

(t), ξ

(t − 2τ), ξ

(t − 2τ)) =







0 g







(t) +







0 0







(t − 2τ),

(t, ξ

(t), ξ

(t − 2τ)) =



−c

sinz

(t) +K

sin p

(t)

sin p

(t − 2τ)



with,

= (1 + c

)ω

(t),

= −ω

(t),

= − f

= ω

(t − 2τ),

= c

(t)

cos(sz

(t))ds + v

(t)

sin(sz

(t))ds,

= (v

(t) −c

(t))

cos(sz

(t))ds,

= −K

(t)

cos(sp

(t))ds,

= K

(t)

cos(sp

(t))ds,

= (v

(t − 2τ) +c

(t − 2τ) −c

(t − 2τ)z

(t − 2τ))

sin(sp

(t))ds,

= (v

(t − 2τ) +c

(t − 2τ) −c

(t − 2τ)z

(t − 2τ))

cos(sp

(t))ds,

= c

(t)

cos(sz

(t − 2τ))ds,

= −c

(t)

cos(sz

(t − 2τ))ds,

= −K

(t)

cos(sp

(t − 2τ))ds,

= K

(t)

cos(sp

(t − 2τ))ds.

The deﬁnition of a persistently exciting (PE) signal

is required in order to establish the stability of the

cascaded system (15)-(16).

Deﬁnition 1. A continuous function ω : R

→ R

is said to be persistently exciting (PE) if ω(t) is

bounded, Lipschitz, and constants δ

> 0 and ε > 0

exist such that,

∀t ≥ 0, ∃s : t − δ

≤ s ≤ t such that |kω(s)| ≥ ε.

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

It is assumed that the desired rotational velocity

, i = 1, 2 is PE. Consequently, the time varying

term ω

(t − 2τ), in the matrix function A

(t,t − 2τ)

may be renamed as

(t), resulting in a matrix

(t).

Note that the matrix function, although time-varying,

will always have entries in the same positions. From

a practical viewpoint the matrix’s entry values will

change with time, but not its structure.

The following theorem establishes the local

stability of the equilibrium point (z

(t), p

(t)) = 0,

and hence the fulﬁllment of the control objectives.

Theorem 1. Consider a unicycle-type mobile robot

subject to a bilateral time-delay 2τ with a posture

kinematic model given by (7). Suppose that the

robot’s reference trajectory is generated by an exosys-

tem with dynamics (2). The estimator (9) together

with the correcting term (13) are used to generate

the system’s control input (14), which is applied to

the robot after a delay τ. Suppose that the reference

rotational velocity ω

(t) is PE, that the controller

gains satisfy c

> 0, c

> 0, and c

> −1, and that

the correcting term gains satisfy K

, K

< 0. If

• subsystem

(t) =

(t)ξ

(t) + A

(t − 2τ) in

(15) is at least locally exponentially stable (LES);

• function g in (15) is bounded;

• system (16) is LES;

then the equilibrium point (z

(t), p

(t)) = 0 of the

closed-loop error dynamics (15)-(16) is LES.

Proof. For the sake of brevity only a sketch of the

proof will be provided.

The theorem is derived from the results for

cascaded systems presented in (Panteley and Lor

ıa,

1998), which have been successfully applied to the

tracking control of a mobile robot in (Jakubiak et al.,

2002) and to the mutual synchronization of two robots

in (van den Broek et al., 2009).

3.2.1 Stability of ξ

(t) = 0

Subsystem

(t) in (15) is a linear time-varying

(LTV) system which can be separated as follows,



˙z

(t)

˙z

(t)





−c

(1 + c

)ω

(t)

−ω

(t) 0



(t)





0 K



(t)



, (17)



˙p

(t)

˙p

(t)





(t)

−

(t) 0



(t)





0 K



(t − 2τ)



. (18)

Note that the output of system (18) perturbs

system (17) in a similar way as in the cascaded struc-

ture (15)-(16). Nevertheless, the coupling term in (17)

will vanish if (18) converges to zero. The reason for

this is that the coupling term does not depend on z

(t)

or z

(t), which is not the case of the coupling term in

(15)-(16), which includes ξ

and ξ

. Consequently,

the stability of

(t) =

(t)ξ

(t) + A

(t − 2τ) can

be established by proving the stability of (17) and (18)

separately.

The time-delay in (18) is approximated by a Tay-

lor series expansion and the stability of the subsystem

is established using the resulting characteristic poly-

nomials, which require that K

, K

< 0.

Knowing that the coupling term vanishes, the

stability of the ﬁrst term in (17) has already been

studied in (van den Broek, 2008) and (van den Broek

et al., 2009), and can be established by a well-known

result in the adaptive control ﬁeld for LTV systems.

The requirement is that that ω

(t) be PE and that the

controller gains satisfy c

> 0 and c

> −1.

3.2.2 Assumption on g

The approach taken here is to express the indetermi-

nate forms in g

i j

cos(sx)ds =

(

sin(x)

for x 6= 0

1 for x = 0

sin(sx)ds =

(

1−cos(x)

for x 6= 0

0 for x = 0

as,

lim

x→0

sin(x)

= 1, lim

x→0

1−cos(x)

= 0.

(19)

by applying L’Hopital’s rule. Using (19) and the prop-

erties of vector norms, and given that the Frobenius

norm and the 2-norm are consistent, it is possible to

obtain explicit expressions for the bounds on g

i j

3.2.3 Local Exponential Stability of ξ

(t) = 0

Consider subsystem

(t) = f

(t, ξ

(t), ξ

(t − 2τ)).

Clearly, ˙p

(t) = K

sin p

(t − 2τ) can be linearized

and will be exponentially stable provided K

< 0. On

the other hand, ˙z

(t) = −c

sinz

(t) + K

sin p

(t)

can also be linearized. As with

(t), ˙z

(t) is

perturbed through a coupling term that will vanish

as ˙p

(t) converges to zero. Requiring that c

0 will ensure exponential stability of the remaining

linearized dynamics. This completes the proof.

REMOTE CONTROL OF A MOBILE ROBOT SUBJECT TO A COMMUNICATION DELAY

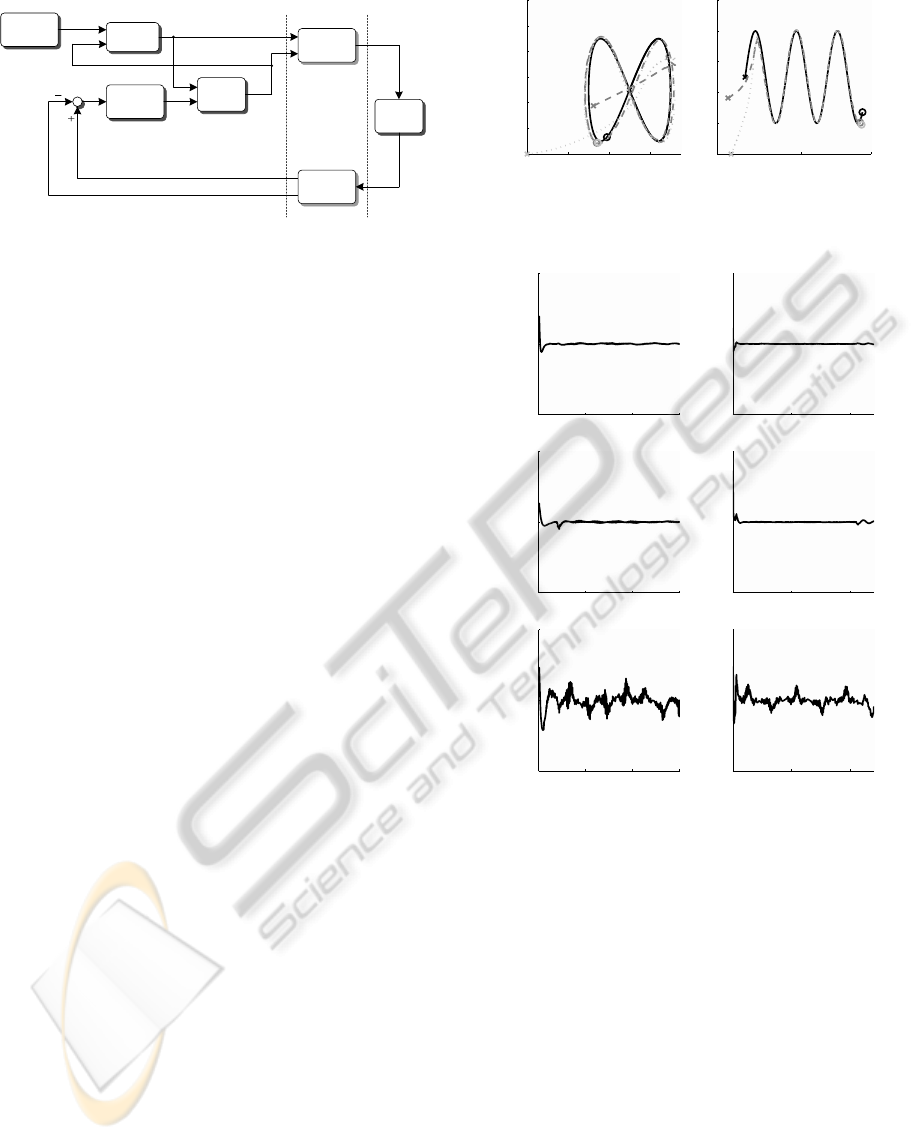
4 EXPERIMENTAL RESULTS

Two equivalent multi-robot platforms exist at the

Eindhoven University of Technology (TU/e) and at

the Tokyo Metropolitan University (TMU). The bilat-

eral time-delay compensation scheme is implemented

in them, meaning that a mobile robot located at TU/e

can be controlled from TMU and viceversa.

4.1 Experimental Platform Description

The experimental platforms’ design objectives

encompass cost, reliability and ﬂexibility. The

hardware and software choices together with the

implementation of the setup at TU/e are discussed

in greater detail in (van den Broek, 2008) (cf. Fig.

3). The setup has already been used to implement

cooperation, coordination, collision avoidance and

servo vision algorithms. The platform at TMU has

similar characteristics, only differing from the one at

TU/e in its size and vision calibration algorithm.

“ﬁg˙setup˙temp” — 2009/9/16 — 10:26 — page 1 — #1

Figure 3: Experimental setup at TU/e.

Mobile Robot. The unicycle selected is the e-puck,

(Mondada et al., 2009), whose wheels are driven

by stepper motors that receive velocity control com-

mands over a BlueTooth connection.

Vision. Each robot is ﬁtted with a ﬁducial marker of

7 by 7 cm, collected by an industrial FireWire cam-

era, interpreted in the program reacTIVision (reac-

TIVision, 2009), and calibrated by means of a global

transformation (TU/e) or a grid (TMU).

Driving Area. The driving area is of 175 × 128 cm

for TU/e and 100×50 cm for TMU, and is determined

based on the required accuracy, the camera lens, and

the height at which the camera is positioned.

Software. The e-puck robots and reacTIVision’s

data stream can be managed in C, Python, or Mat-

lab script. In this work, the controller implementa-

tion and signal processing is carried out in Python,

(Python, 2009).

Bandwidth and Sampling Rate. Using vision as

the localization technique diminishes the system’s

bandwidth and results in a sampling rate of 25Hz.

4.2 Data Exchange over the Internet

Due to its widespread availability and low cost, the

Internet is chosen as the communication channel to

exchange data between TU/e and TMU.

Data Exchange. A Virtual Private Network (VPN)

is established between TU/e and TMU in order to

implement a reliable and secure data exchange.

Socket Conﬁguration. Data is exchanged between

TU/e and TMU as soon as it becomes available

using non-blocking Transmission Control Protocol

(TCP) sockets running the Internet Protocol (IP). The

system’s low bandwidth allows the use of the TCP,

which guarantees reliable and orderly data delivery.

Data Payload. The variables exchanged amount to

the current time instant and control signals from the

control side to the system, and to the position and ori-

entation values from the system side to the controller.

4.3 Implementation Issues

One of the main implementation issues of the

proposed time-delay compensation strategy is the

accurate modeling and characterization of the

time-delay induced by the communication chan-

nel. The use of predictor-like schemes is often

discouraged because of their sensitivity to delay

model mismatches, (Hokayem and Spong, 2006),

specially when considering nonlinear systems and a

communication channel such as the Internet. To this

end, three methods that ease the implementation of

the proposed compensation strategy are suggested.

Their objective it to bring

τ as close as possible to

τ in practice.

Delay Measurement. The round trip delay between

TU/e and TMU (and viceversa) has been measured

during different times of the day, for a variable

amount of time, and for a total time of around 60min.

The mean delay value is approximately 265ms for

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

“ﬁg˙pred˙bi˙no˙model˙temp” — 2010/2/3 — 0:52 — page 1 — #1

Communication

channel

Reference

Trajectory

Controller

Mobile

Robot

State

Predictor

Correcting

Term

Forward

time-delay

Backward

time-delay

Figure 4: Time-delay compensation scheme block diagram

representation without time-delay models.

both cases (267.4917ms TU/e-TMU, 269.5307ms

TMU-TU/e). Occurrences of delays greater than

300ms where of 0.27% for TU/e-TMU and 0.34%

for TMU-TU/e. Thus, the round trip delay can be

modeled with enough accuracy even if the Internet is

considered as the communication channel.

Time-stamping. Outgoing and incoming data on

the controller side can be time-stamped in order to

estimate the round trip delay for each pair of control

signals and sensor data, setting the estimator’s delay

model accordingly.

Signal Bouncing. The estimator’s output may be

sent together with the control signals to the mobile

robot, and then sent back to the controller without

being modiﬁed. By using the communication chan-

nel itself to delay the estimator’s output, modeling the

time-delay is no longer necessary (cf. Figure 4).

4.4 Experiments

In the ﬁrst experiment a mobile robot at TMU is

controlled from TU/e. The reference trajectory is a

lemniscate with center at [0.5m, 0.25m], a length and

width of 0.2m, and a velocity multiplier of 0.2m/s.

The scenario repeats in the second experiment, where

a sinusoid with origin at [0.1m, 0.25m], an amplitude

of 0.15m, an angular frequency of 0.3rad/s, and a ve-

locity multiplier of 0.01m/s constitutes the reference.

The system’s initial condition is q(0) =

[0.3235m 0.1882m 0.2851rad]

for the ﬁrst ex-

periment and q(0) = [0.0225m 0.1821m 0.3916rad]

for the second one. In both cases the estimator’s

initial condition is set to z(0) = [0 0 0]

, the controller

gains to c

= 1.0, c

= c

= 2.0 and the correcting

term gains to K

= K

= −0.6. The sampling

rate is 25Hz and the experiments’ duration is 60sec

and 120sec respectively. The round trip delay is

modeled as 265ms based on measurements, although

the estimator’s output is in fact delayed 280ms since

0 0.2 0.4 0.6

0.1

0.2

0.3

0.4

0.5

0.6

X [m]

Y [m]

0 0.5 1

0.1

0.2

0.3

0.4

0.5

X [m]

Y [m]

Figure 5: Reference, robot and predictor behavior in the X-

Y plane for two different trajectories.

0 20 40 60

−0.5

0.5

t [s]

[m]

0 20 40 60

−0.5

0.5

t [s]

[m]

0 20 40 60

−0.5

0.5

t [s]

[rad]

0 50 100

−0.5

0.5

t [s]

[m]

0 50 100

−0.5

0.5

t [s]

[m]

0 50 100

−0.5

0.5

t [s]

[rad]

Figure 6: Practical convergence of the correcting terms.

only delay models which are multiples of 0.04 are

allowed due to the setup’s sampling time, meaning

data is displaced 7 locations within the storage buffer.

The experimental results are shown in Figure 5

and 6 for both experiments. The ﬁrst plots show the

reference (black), robot (gray) and predictor (light

gray) trajectories in the X-Y plane, with their initial

and ﬁnal position marked with a cross and a circle

respectively. The plots in Figure 6 show the evolution

of the correcting terms ν

(t), ν

(t), and ν

(t) and how

they practically converge to zero even in the presence

of a delay model mismatch and considering a time-

varying communication channel. The behavior of the

proposed delay compensation strategy is consistent

with the stability analysis presented and the tracking

performance of the robot can be ensured even under a

bilateral time-delay.

REMOTE CONTROL OF A MOBILE ROBOT SUBJECT TO A COMMUNICATION DELAY

5 DISCUSSION

A compensation strategy to account for the negative

effects of a bilateral time-delay affecting a unicycle-

type mobile robot has been proposed. Several tech-

niques to accurately reproduce the time-delay in the

estimator have been presented, since this is required

and often a cause of concern in predictor-like control

strategies. Experiments show that the delay compen-

sation strategy is robust to small delay model mis-

matches and delay variations using the Internet as a

communication channel.

Future work includes a robustness analysis of

the delay compensation scheme and a comparison

with other predictor-like strategies. Additionally,

techniques to synchronize as precisely as possible

the controller and system sides are being studied in

order to obtain a more accurate measurement of the

system’s performance. Integrating the concept of

remote control of mobile robots with notions related

to the long distance synchronization of robotic net-

works and extending the concepts of the estimator to a

more general setting (other mechanical systems) also

remain topics to be addressed in the future.

ACKNOWLEDGEMENTS

The ﬁrst author would like to dedicate this paper to

his father, Prof. Jaime Alvarez-Gallegos of CINVES-

TAV, M

exico, who was recently honored because of

his 60th birthday. Additionally, the authors acknowl-

edge the help of Hisashi Katsumata in conducting ex-

periments. This work has been supported by CONA-

CYT and SEP, M

exico, by the Graduate School of

Science and Engineering at TMU and the Japan So-

ciety for the Promotion of Science (JSPS) through

Grant-in-Aid for Scientiﬁc Research (No. 20560424).

REFERENCES

Brockett, R. (1983). Differential geometric control theory,

chapter Asymptotic stability and feedback stabiliza-

tion, pages 181–191. Birkh

auser.

Heemels, W. P. M. H., Teel, A. R., van de Wouw, N., and

Nesic, D. (2010). Networked control systems with

communication constraints: Tradeoffs between sam-

pling intervals, delays and performance. IEEE Trans.

Automat. Contr., Accepted.

Hokayem, P. F. and Spong, M. W. (2006). Bilateral

teleoperation: An historial survey. Automatica,

42(12):2035–2057.

Jakubiak, J., Lefeber, E., Tch

on, K., and Nijmeijer, H.

(2002). Two observer-based tracking algorithms for

a unicycle mobile robot. Int. J. Appl. Math. Comput.

Sci., 12(4):513–522.

Kanayama, Y., Kimura, Y., Miyazaki, F., and Noguchi, T.

(1990). A stable tracking control method for an au-

tonomous mobile robot. In Proc. IEEE Int. Conf. Rob.

Automat. (ICRA), pages 384–389.

Kojima, K., Oguchi, T., Alvarez-Aguirre, A., and Nijmeijer,

H. (2010). Predictor-based tracking control of a mo-

bile robot with time-delays. In Proc. 8th IFAC Sympo-

sium on Nonlinear Control Systems (NOLCOS). (Ac-

cepted).

Kostic, D., Adinandra, S., Caarls, J., van de Wouw, N., and

Nijmeijer, H. (2009). Collision-free tracking control

of unicycle mobile robots. In Proc. 48th IEEE Conf.

Dec. Control (CDC/CCC), pages 5667–5672.

Mondada, F., Bonani, M., Raemy, X., Pugh, J., Cianci, C.,

Klaptocz, A., Magnenat, S., Zufferey, J.-C., Floreano,

D., and Martinoli, A. (2009). The e-puck, a robot de-

signed for education in engineering. In Proc. 9th Con-

ference on Autonomous Robot Systems and Competi-

tions, pages 59–65.

Niemeyer, G., Preusche, C., and Hirzinger, G. (2008).

Springer Handbook of Robotics, chapter 31: Teler-

obotics, pages 741–758. Springer-Verlag.

Oguchi, T. and Nijmeijer, H. (2005a). Control of nonlinear

systems with time-delay using state prediction based

on synchronization. In Proc. EUROMECH Nonlinear

Dynamics Conference (ENOC), pages 1150–1156.

Oguchi, T. and Nijmeijer, H. (2005b). Prediction of

chaotic behavior. IEEE Trans. on Circ. and Syst. I,

52(11):2464–2472.

Oguchi, T. and Nijmeijer, H. (2006). Anticipating synchro-

nization of nonlinear systems with uncertainties. In

6th IFAC Workschop on Time-Delay Systems.

Panteley, E., Lefeber, E., Lor

ıa, A., and Nijmeijer, H.

(1998). Exponential tracking control of a mobile car

using a cascaded approach. In IFAC Workshop on Mo-

tion Control.

Panteley, E. and Lor

ıa, A. (1998). On global uniform

asymptotic stability of nonlinear time-varying systems

in cascade. Syst. Contr. Lett., 33(2):131–138.

Python (2009). Python Programming Language.

http://www.python.org.

reacTIVision (2009). reacTIVision 1.4: A

toolkit for tangible multi-touch surfaces.

http://reactivision.sourceforge.net/.

Tipsuwan, Y. and Chow, M.-Y. (2003). Control methodolo-

gies in networked control systems. Contr. Eng. Pract.,

11(10):1099–1111.

van den Broek, T. (2008). Formation Control of Unicycle

Mobile Robots: Theory and Experiments. Master’s

thesis, Eindhoven University of Technology.

van den Broek, T., van de Wouw, N., and Nijmeijer, H.

(2009). Formation control of unicycle mobile robots:

A virtual structure approach. In Proc. 48th IEEE Conf.

Dec. Control (CDC/CCC), pages 3264–3269.

Voss, H. U. (2000). Anticipating chaotic synchronization.

Phys. Rev., 61(15):5115–5119.

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics