A PARALLEL VERSION OF THE MPEG-2 ENCODING
ALGORITHM FORMALLY ANALYZED USING ALGEBRAIC
SPECIFICATIONS
Katerina Ksystra, Petros Stefaneas
School of Electrical and Computer Engineering, National Technical University of Athens, Athens, Greece
School of Applied Mathematical and Physical Sciences, National Technical University of Athens, Athens, Greece
Iakovos Ouranos, Panayiotis Frangos
School of Electrical and Computer Engineering, National Technical University of Athens, Athens, Greece
Keywords: MPEG-2 encoding algorithm, Parallel algorithm, CafeOBJ, Observational Transition System.
Abstract: MPEG-2 is a wide used group of standards, established by the Moving Picture Experts Group (MPEG), for
the digital compression of broadcast-quality full-motion video. Due to its high acceptance, it is very
important to ensure that it behaves in a correct manner. To avoid vulnerability problems the MPEG-2
encoding algorithm has been already formally specified and verified for its correctness. In this paper, we
propose the use of the OTS/CafeOBJ Method in order to prove that two MPEG-2 encoding algorithms for
the same input produce the same output. Our approach is based on a simplified parallel version of the
MPEG-2 encoder. Also, we have proved a mutual exclusion property for this parallel algorithm.
1 INTRODUCTION
Formal methods are techniques based on
mathematical theories that can be used to prove
desirable system properties. The need for applying
formal methods to specify and verify encoding
protocols and systems has increased, as encoders
evolve and become more and more complex. The
sequential MPEG-2 encoding algorithm has been
specified, using the OTS/CafeOBJ formal
methodology (Ksystra et. al, 2009). We have proved
some important invariant properties. 1) If the frame
A belongs to the output buffer and it is an I-frame
then it is the coded I frame of the GoP. 2) If the
frame A belongs to the output buffer and it is a P-
frame then it is the coded P frame of the GoP. 3) If
the frame A belongs to the output buffer and it is a
B-frame then it the coded B-frame of the GoP. The
verification of invariants 1-3 proves that for any
input the output of the encoding algorithm is as
expected and consecutively that the algorithm
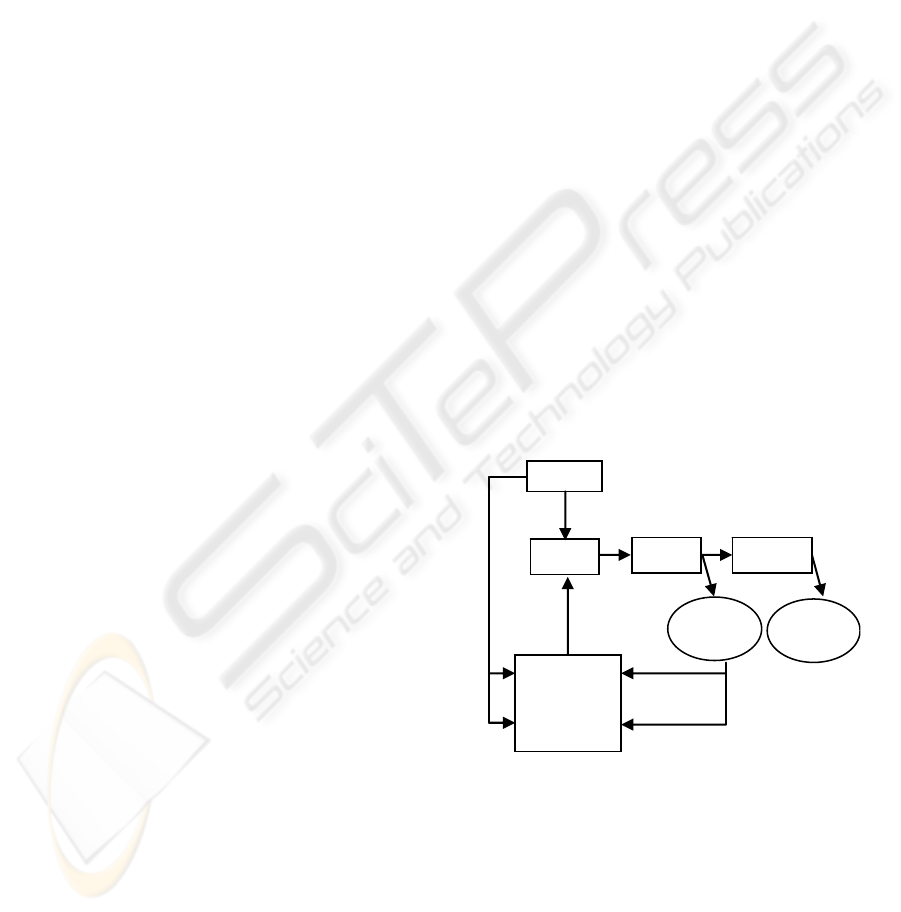
behaves in a correct manner. In the following figure
we present the sequential MPEG-2 encoding
algorithm:
Figure 1: Diagram of the sequential MPEG-2 encoding
algorithm.
We propose the use of the OTS/CafeOBJ
Method as a means of comparison between MPEG-2
encoding algorithms. More precisely, we have
demonstrated that this method can be used to prove
that two algorithms, the MPEG-2 sequential
algorithm and a simplified partially parallel version
of it are equivalent i.e., for the same input produce
the same output. The parallel algorithm presented
dct-q
vlc
idct-iq
I
,
P
I
I
input
output
buffer
P
B
motion vector
prediction error
Frame
Store
35
Ksystra K., Stefaneas P., Ouranos I. and Frangos P. (2010).
A PARALLEL VERSION OF THE MPEG-2 ENCODING ALGORITHM FORMALLY ANALYZED USING ALGEBRAIC SPECIFICATIONS.
In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 35-38
DOI: 10.5220/0002944600350038
Copyright
c
SciTePress

here is used only for demonstration purposes and is
constrained to a specific input. This is done in order
to simplify the specification process. The rest of the
paper is organized as follows: In section 2 we briefly
introduce the OTS/CafeOBJ method. In section 3 we
present the parallel encoding algorithm and its
specification as an OTS in CafeOBJ while section 4
presents the verification of the invariants and the
corresponding proof scores. Finally, section 5
concludes the paper.
2 THE OTS/CAFEOBJ METHOD
2.1 Observational Transition Systems
Assuming that there exists a universal state space
called Y and that each data type used, has been
defined in advance, an Observational Transition
System (OTS) (Ogata, 2006), is a triplet <O,I, T >
that defines a transition system written in terms of
equations. O denotes a finite set of observers, i.e.
functions from the state space to a data type. I
denotes the set of the initial states, such that I is a
subset of the state space Y, and finally T is a set of
conditional transition rules. Each is a function
: , such that
for each
,
/
. The condition
of τ is called the
effective condition.
2.2 OTS in CafeOBJ
CafeOBJ (Diaconescu, 1998, CafeOBJ Home Page)
is an algebraic specification language that can be
used to specify abstract data types as well as abstract
state machines. An OTS is described in CafeOBJ.
The key component in a specification is a module.
Each module defines a sort, a CafeOBJ term
describing abstract data types with multiple
inheritance and operational semantics based on term
rewriting (Diaconescu, 2000). A visible sort denotes
an abstract data type while a hidden sort (Goguen,
1997) the state space of an abstract machine. Two
kinds of operators can be applied to hidden sorts,
action operators that change the state of an abstract
machine and correspond to transitions and
observation operators that are used to observe some
key values that define the inside of the abstract
machine and correspond to observers. Declarations
of observation and action operators start with bop or
bops, and those of other operators with op or ops.
Declarations of equations start with eq, and those
of conditional ones with ceq. So typically an action
operator corresponding to transition τ
j1,...,jn
∈
T is
declared in CafeOBJ as bop a : H Vj1 ... Vjn -> H,
where H is the hidden sort denoting the state space
and Vj1 ... Vjn are the visible sorts (date types) that
parameterize this action operator .
3 ALGEBRAIC SPECIFICATION
OF THE PARALLEL
ALGORITHM
3.1 Parallel Encoding Algorithm
There are some encoding steps of the MPEG-2 that
may proceed in parallel. Based on this we present an
encoding algorithm which is partially parallel, i.e.,
that only some parts of the encoding process can be
simultaneously computed by different processors
(most of the processes presuppose other encoding
steps). For example, in the model shown in table 1
below, we use two processors. To simplify the
specification of this parallel algorithm we will
consider as input the Group of pictures: IBBP, where
the actual encoding order is IPBB.
When the input is I on processor C1, the Discrete
Cosine Transform is applied on each macroblock
and then comes the Quantization. After quantization,
comes the encoding using a variable length code and
is sent to the output buffer, on C1. At the same time
the Inverse Quantization and the Inverse DCT give
us a compressed picture which is stored in the Frame
Store (FS), on C2. When the input is P, the motion
vector and the prediction error are computed using
the frame stored in FS, on C1. Then, these are coded
following the same steps as for the I frame. After the
coding of the reference frames (I,P) the first B frame
is encoded on C1 and the second on C2.
Table 1: Data flow table of the parallel algorithm.
C1
dct-q(I) Iq-idct(I) dct-q(P) iq-idct(P) encode(B1)
C2
vlc(I) vlc(P) encode(B2)
3.2 OTS Model and Specification
The observers we will use are: Q which observes the
content of the output buffer at any given time. Iqi
which returns the result of the Inverse Quantization
and Inverse DCT process on the I-frame. Iqp which
returns the result of the Inverse Quantization and
Inverse DCT process on the P-frame. Dctqi which
returns the result of the Discrete Cosine Transform
and the Quantization process on the I-frame. Dctqp
SIGMAP 2010 - International Conference on Signal Processing and Multimedia Applications
36

which returns the result of the Discrete Cosine
Transform and the Quantization process on the P-
frame. Pc which observes in which state we are, and
busy which checks in every state whether the
processor is busy or not. Finally, we use a variable
(C) which takes a value from the set of constants
{C1,C2} and declares which of the two processors
we want to use.
The transitions we used in order to specify the
parallel encoding algorithm are the following: dctqI,
decodeI, dctqP, decodeP, vlcI, vlcP, encodeB1,
encodeB2 and finish1.
4 VERIFICATION OF THE
PARALLEL ALGORITHM
Our main intent is to show that the formal
verification can be used to verify that a parallel
version is identical to the original serial one. To this
end, we have formally verified that the two
algorithms produce the same output, given the same
input by showing that the invariants proved for the
sequential algorithm also hold for the parallel.
In order to prove such properties in CafeOBJ,
several steps need to be taken (Ogata 2008,
Futatsugi, 2005).
First, we express the property in a formal way as
a predicate, say invariant inv1(p,x), where p is a free
variable for states and x denotes other free variables
of inv1.
Then, we write a module, usually called INV,
where inv1(p,x) is expressed as a CafeOBJ term.
op inv1 : Sys Frame Frame -> Bool
eq inv1(S,A,I)=((A in q(S)and isI(A)
and (I=i))implies A=I(vlc(dctq(I)))) .
Show that inv1 holds for any initial state, say
init, with the following proof score:
open INV
red inv1(init,a,i') .
close
where red is a command that reduces a given term
by regarding declared equations as left-to-right
rewrite rules.
Write the inductive step where s’ denotes the
successor state of s.
op istep1 : -> Bool
eq istep1 = inv1(s,a,i') implies
inv1(s',a,i') .
Check for each transition rule if the inductive step
holds.
open ISTEP
op k : -> Frame .
eq s' = vlci(s,k&l&m&n).
red istep1 .
close
If istep1 is reduced to true then, the transition
preserves the invariant. The above case returns
neither true nor false. CafeOBJ returns a clause that
contains as a sub clause the effective condition. This
means that the machine cannot reduce whether or
not the effective condition holds under the given
equations. In this case we need to apply case
splitting to help CafeOBJ reduce this case. To this
end, we split the effective condition.
open ISTEP
op k : -> Frame .
eq c-vlci(s,k&l&m&n) =false.
eq s' = vlci(s,k&l&m&n) .
red istep1 .
close
The above refers to the case that the effective
condition is false and CafeOBJ returns true. Now we
must cover its symmetrical one, i.e.
c-vlci
(s,k&l&m&n)=true. Again CafeOBJ returns
neither true nor false. Following the same approach
we reach the following state:
dci(s)=dctq(k)
∧
(
c=c2)
∧
(k = i)
∧
¬
busy(s,c)
∧
¬
(a= I(vlc(dctq(i'))))
∧
(a = I(vlc(dctq(k))))
∧
(i = i')
Here CafeOBJ has returned true, for all the
symmetrical sub cases but returns neither true nor
false for this state. Normally we would, and can,
apply more case splitting, but we notice that these
predicates cannot hold simultaneously in our OTS
(computer - human interactive proving procedure).
So we can use these contradicting predicates to
conjure a lemma and discard this case. These
predicates constitute lemma 1 of table 2. Using this
lemma we can discard this case with the following
proof passage:
open ISTEP
op k : -> Frame .
eq (dci(s) = dctq(k)) = true .
eq (c = c2) = true .
eq (k = i) = true .
eq busy(s,c) = false .
eq (a = I(vlc(dctq(i')))) = false .
eq (a = I(vlc(dctq(k)))) = true .
eq (i = i') = true .
A PARALLEL VERSION OF THE MPEG-2 ENCODING ALGORITHM FORMALLY ANALYZED USING
ALGEBRAIC SPECIFICATIONS
37

eq s' = vlci(s,k&l&m&n) .
red inv5(a,i,i',k) implies istep1.
Close
CafeOBJ returns true for the above proof passage
and hence, once we prove lemma 1 (table 2), this
concludes the proof for the vlci transition rule of
our safety property. Applying the same technique,
CafeOBJ returned true for all transitions. Finally, all
the lemmas were proven and thus our proof
concludes. Following the procedure presented
above, 16 lemmas were discovered and used. In
table 2 we present some of the most characteristic
ones.
Table 2: Most important lemmas.
Most important Lemmas/Invariants
1. If A is equal to I(vlc(dctq(K)) and not equal to
I(vlc(dctq(I’)))) then K is not equal to I and I is not
equal to I’.
2. If A is a coded I frame that implies that it is not an
Bframe.
3. If A is equal to P(vlc(dctq(est(I,P)+comp(I,P)) and
not equal to P(vlc(dctq(est(I’,P’)+comp(I’,P’)) that
implies that P(vlc(dctq(est(I,P) +comp(I,P)) is not
equal to P(vlc(dctq(est(I’,P’) + comp(I’,P’))
5 CONCLUSIONS
We have presented briefly a methodology for
comparing two encoding algorithms using the
specification of a simplified parallel version of the
MPEG-2 Encoding Algorithm as an Observational
Transition System in CafeOBJ. Several alternative
versions of the MPEG-2 encoding algorithm have
been proposed as it is a wide used protocol
(Cambronero, 2005) but to our knowledge we are
the first to apply the OTS/CafeOBJ method to this.
Our work is part of a bigger research project
(Triantafyllou et. al, 2009, Ouranos et. al 2007,
Ouranos et. al 2007) in modeling and specification
of algorithms and protocols using algebraic
specification languages. In the future we plan to
apply this formal approach to other video encoding
standards such as the MPEG-4.
REFERENCES
Diaconescu, R., Futatsugi, K., 1998. CafeOBJ Report. In
World Scientific.
Goguen, J. A., Malcolm, G., 1997. A Hidden Agenda. In
Technical Report. University of California at San
Diego.
Diaconescu, R., 2000. Behavioral Coherence in Object -
Oriented Algebraic Specification. In J.Universal
Computer Science. 6(1). pp. 74-96.
Ogata, K., Futatsugi, K., 2006. Some Tips on Writing
Proof Scores in the OTS/CafeOBJ Method. K.
Futatsugi, J.-P. Jouannaud, J. Meseguer (Eds.),
Algebra, Meaning, and Computation, Essays
Dedicated to Joseph A. Goguen on the Occasion of
His 65th Birthday, LNCS 4060, pp. 596-615, Springer.
Ogata, K., Futatsugi, K., 2008. Simulation-based
Verification for Invariant Properties in the
OTS/CafeOBJ Method. In Electronic Notes Theor.
Comp. Science 20. pp. 127-154.
Futatsugi, K., Goguen, J.A., Ogata, K., 2005. Verifying
Specifications with Proof Scores in CafeOBJ. B.
Meyer, J. Woodcock (Eds.), Verified Software:
Theories, Tools, Experiments, First IFIP TC 2/WG 2.3
Conference, VSTTE, LNCS 4171, pp. 277-290.
Cambronero, M., Ravn, A.P., Valero, V., 2005. Using
UPPAAL to analyse an MPEG-2 algorithm. In
Proceedings of VII Workshop Brasileiro de Tempo
Real. Fortaleza (Brasil). pp. 73-82.
Triantafyllou, N., Ouranos, I., Stefaneas, P., 2009.
Algebraic Specifications for OMA REL Licences. In
Wimob‘09, IEEE International Conference on
Wireless and Mobile Computing, Networking and
Communications. pp.376-381.
Ouranos, I., Stefaneas, P., Frangos P., 2007. An Algebraic
Framework for Modeling of Mobile Systems. In
IEICE Trans. Fund., Vol. E90-A, No. 9, pp. 1986-
1999.
Ouranos, I., Stefaneas, P., 2007. Verifying Security
Protocols for Sensor Networks using Algebraic
Specification Techniques. In CAI’07, Thessalonica,
Greece, LNCS 4728, pp. 247-259, Springer.
Ksystra, K., Stefaneas, P., Triantafyllou, N., Ouranos, I.,
2009. An Algebraic Specification for the MPEG-2
Encoding Algorithm. In SEEFM’09, Formal Methods
for Web Services Formal Methods for Agent-based
Systems. Thessalonici, Greece. (presented)
CafeOBJ Home Page http://www.ldl.jaist.ac.jp/cafeobj/.
MPEG Home Page, http://www.mpeg.org.
ISO/IEC 138182
SIGMAP 2010 - International Conference on Signal Processing and Multimedia Applications
38
