STABILITY ANALYSIS FOR BACTERIAL LINEAR METABOLIC
PATHWAYS WITH MONOTONE CONTROL SYSTEM THEORY
Nacim Meslem, Vincent Fromion, Anne Goelzer and Laurent Tournier
INRA, Mathematics, Informatics and Genome Laboratory
Jouy-en-Josas, Domaine de Vilvert 78352 Jouy-en-Josas Cedex, France
Keywords:
Monotone control systems, Negative feedback theorem, Linear bacterial metabolic pathways.
Abstract:
In this work we give technical conditions which guarantee the global attractivity of bacterial linear metabolic
pathways (reversible and irreversible structures) where both genetic and enzymatic controls involve the end
product through metabolic effectors. To reach this goal, we use the negative feedback theorem of the monotone
control systems theory, and we represent all conditions needed to apply the negative feedback theorem to the
bacterial linear metabolic pathways in convenient deduced forms.
1 INTRODUCTION
The bacterial metabolic machinery and its regulation
make up a complex system involving many cellular
components such as metabolites and enzymes. In
this paper, we focus on the dynamical behavior of the
control structures used in a large number of bacterial
biosynthesis pathways where both the genetic and en-
zymatic controls involve the last product as metabo-
lite effector (Goelzer et al., 2008). Stability analysis
of these biological structures is recognized as an issue
of great importance in order to deduce key biological
properties of the bacterial metabolic pathways. In the
literature, many studies focused on the analysis of the
metabolic and genetic networks separately. For in-
stance, using the stability results about cyclic dynam-
ical systems (Tyson and Othmer, 1978), (Sanchez,
2009), (Arcak and Sontag, 2006), one can state nice
stability conditions of the irreversible linear metabolic
pathways with allosteric regulation. One can also use
the stability results about tridiagonal systems (Angeli
and Sontag, 2008), (Wang et al., 2008) to analyze the
stability of the reversible metabolic pathways. How-
ever, few works have considered structures with both
genetic and allosteric regulation. Thus, in this pa-
per we investigate stability of the common structures
shared by many bacteria cells and yeasts. These struc-
tures are called end product structures, because both
genetic and enzymatic controls involve the end prod-
uct of the pathway (Grundy et al., 2003), (Gollnick
et al., 2005), (Goelzer et al., 2008).
We will use the monotone control system theory
developed in (Angeli and Sontag, 2003) to deal with
stability issue of biological systems. In particular,
the negative feedback theorem has been applied to a
model of Mitogen-Activated Protein Kinase (MAPK)
cascades in (Angeli and Sontag, 2003), and more re-
cently to Goldbeter’s circadian model (Angeli and
Sontag, 2008). The main contribution of this work
consists in providing technical conditions to check all
the required assumptions to apply the negative feed-
back theorem to end product structures (under irre-
versible and reversible forms).
This paper is structured as follows. Section 2
presents the mathematical models for the linear re-
versible and irreversible bacterial metabolic pathways
and states the main results of this paper which consist
in propositions 1 and 2. Section 3 recalls some def-
initions and properties of monotone control systems
theory and introduces the negative feedback theorem.
Section 4 addresses the stability analysis of the dy-
namical models introduced in section 2 and proves the
two propositions.
2 LINEAR METABOLIC
PATHWAYS
Consider a linear pathway with n metabolites in-
volved in enzymatic reactions, an input flux ν
1
and
an output flux ν
n
as depicted in Figure 1. Each X
i
and E
i
correspond to a metabolite and an enzyme re-
spectively. We assume that the pool X
1
of the first
22
Meslem N., Fromion V., Goelzer A. and Tournier L. (2010).
STABILITY ANALYSIS FOR BACTERIAL LINEAR METABOLIC PATHWAYS WITH MONOTONE CONTROL SYSTEM THEORY.
In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 22-29
DOI: 10.5220/0002944900220029
Copyright
c
 SciTePress

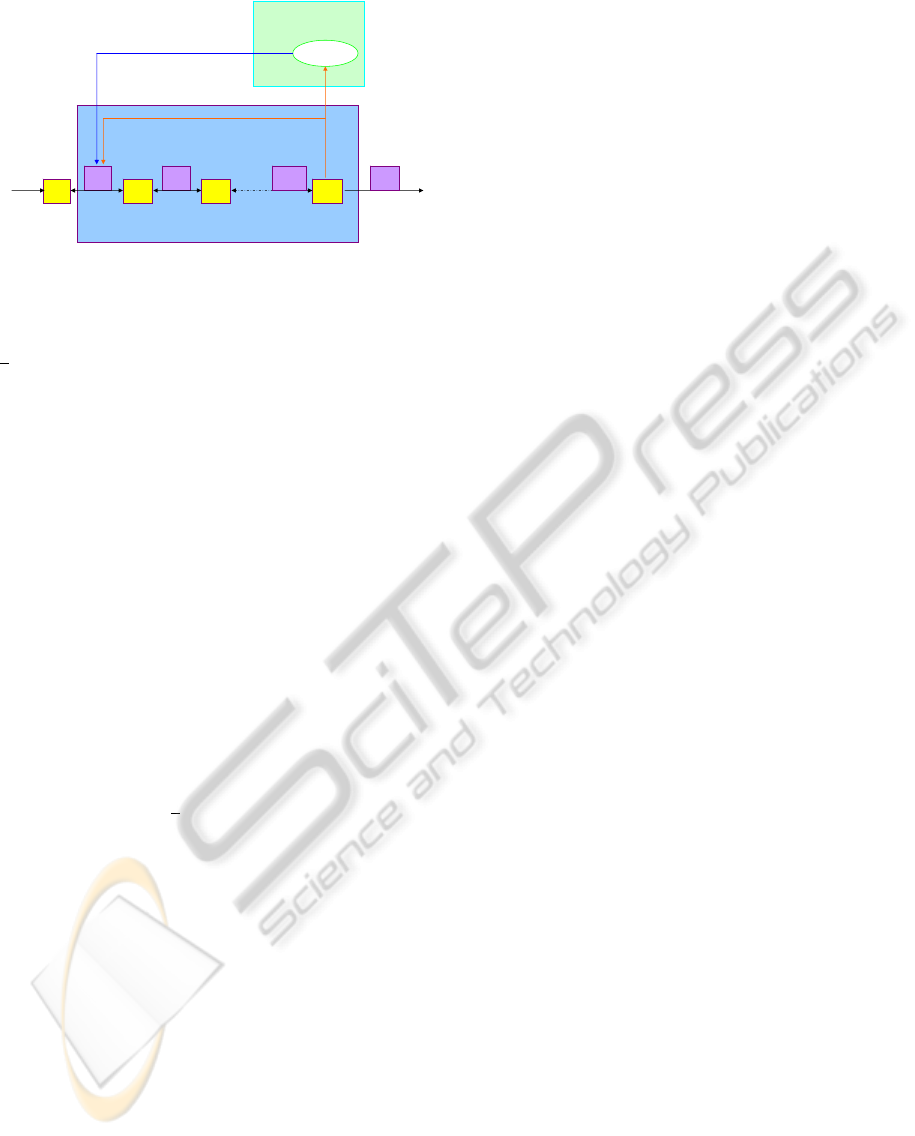
Genetic level
Allosteric regulation
- -
TF on
Metabolic pathway
n
E
V
n
n
X
3
X
2
E
2
X
1
E
1n
−
E
1
X
Genetic regulation
V
1
Output flux
Input flux
Figure 1: End product control linear structure.
metabolite is maintained by the input flux ν
1
which
corresponds to a supply flux. Hence its concentration
x
1
is strictly positive constant. The output of the path-
way is the flux ν
n
which corresponds to the bacterium
requirement for the metabolite X
n
. Hereafter, for each
i ∈ {2, . . . , n} we denote by x
i
the nonnegative con-
centration of the metabolite X
i
, and by E
i
the assumed
constant positive concentration of the enzyme E
i
. The
three phenomena, enzymatic reactions, allosteric reg-
ulation and genetic regulation (with respect to E
1
),
presented in Figure 1 can be described by a set of in-
terconnected nonlinear differential equations. In the
sequel, we analyze global stability of two types of the
interconnected differential equations, namely the re-
versible and irreversible metabolic pathways.
2.1 Reversible Pathways
The common end product structure of linear re-
versible metabolic pathways is described by the fol-
lowing dynamical system:











˙x
2
= E
1
f
1
(x
1
, x
2
, x
n
) − E
2
f
2
(x
2
, x
3
)
˙x
3
= E
2
f
2
(x
2
, x
3
) − E
3
f
3
(x
3
, x
4
)
.
.
.
.
.
.
.
.
.
.
.
.
˙x
n
= E
n−1
f
n−1
(x
n−1
, x
n
) − E
n
f
n
(x
n
)
˙
E
1
= g(x
n
) − µE
1
(1)
where the Lipschitz functions f
i
denote the reaction
rates of the enzymes E
i
. Note that, in the reversible
structures all reaction rates depend on the product and
substrate concentrations and have the following prop-
erties:
• For the first enzyme: we assume that the metabo-
lite X
n
modulates the activity of the enzyme E
1
through, for example, an allosteric effect. The
function f
1
(x
1
, x
2
, x
n
) is increasing in its first ar-
gument and decreasing with respect to its second
and third arguments, and we have for any x
1
> 0,
x
2
≥ 0 and x
n
≥ 0, f
1
(x
1
, x
2
, x
n
) > 0 and for any
x
n
≥ 0, f
1
(0, 0, x
n
) = 0. In addition, there exists
M
1
> 0 such that for any x
1
> 0, x
2
≥ 0 and x
n
≥ 0,
f
1
(x
1
, x
2
, x
n
) ∈ [0, M
1
). We also assume that for
any x
1
> 0 and x
n
≥ 0 there exists x
∗
2
> 0 such
that f
1
(x
1
, x
∗
2
, x
n
) = 0. Finally, for any x
1
> 0 and
x
2
> 0 we have,
lim
x
n
→+∞
f
1
(x
1
, x
2
, x
n
) = 0.
• For the intermediate enzymes: f
i
, i ∈ {2, . . . , n −
1}, is increasing in x
i
and decreasing in x
i+1
.
For any x
i
> 0, f
i
(x
i
, 0) > 0, and for any x
i+1
>
0, f
i
(0, x
i+1
) < 0 and f
i
(0, 0) = 0. Moreover,
there exists M
i
> 0 and M
0
i
≥ 0 such that for any
x
i
> 0 and x
i+1
≥ 0, f
i
(x
i
, x
i+1
) ∈ (−M
0
i
, M
i
). Fi-
nally, we assume that for any x
i
> 0 there exists
x
∗
i+1
> 0 such that f
i
(x
i
, x
∗
i+1
) = 0.
• For the final enzyme: E
n
describes the properties
of the remainder part of the metabolic network
and summarizes the relation between the flux sup-
plied by the pathway and the final concentration.
The properties of f
n
mainly depends on the prop-
erties of the next modules, and generally f
n
is a
strictly increasing, positive and bounded function
in x
n
such that
f
n
(0) = 0, lim
x
n
→+∞
f
n
(x
n
) = M
n
.
The dynamics of the enzyme concentrations during
the exponential growth phase are mostly the result of
two phenomena: (i) the de novo production (ii) the di-
lution effect caused by the increase of the cell volume.
For this, in the last equation of (1), we have consid-
ered that the control of the concentration of the first
enzyme is regulated by the concentration of the final
metabolite x
n
, where µ is the growth rate of the bac-
terium assumed to be in the exponential growth phase.
The term g(x
n
) corresponds to the instantaneous pro-
duction of the enzyme E
1
modulated by a metabolite
(implicitly through a transcription factor). The con-
tinuous function g(.) is positive strictly decreasing in
the end product x
n
with g(0) = g
max
, g
max
> 0 and
lim
x→+∞
g(x) = 0.
After the detailed description of the dynamical
model of the linear reversible metabolic pathway, we
state below the main results of this paper about its
global attractivity.
Stability Results. Let us start by setting three hy-
potheses and then we introduce our first proposition.
• Hypothesis H
1
: The n−1 × n − 1 Tridiagonal ma-
trix,
STABILITY ANALYSIS FOR BACTERIAL LINEAR METABOLIC PATHWAYS WITH MONOTONE CONTROL
SYSTEM THEORY
23

Q =












q
2,2
q
2,3
0 . .. . . . 0
q
3,2
q
3,3
q
3,4
.
.
.
.
.
.
0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0
.
.
.
.
.
.
q
n−1,n−2
q
n−1,n−1
q
n−1,n
.
.
. . . . . . . 0 q
n,n−1
q
n,n












where ∀i, j ∈ {2, . . . , n}
q
i, j
= sup

∂(E
i−1
f
i−1
(.) − E
i
f
i
(.))
∂x
j

,
is Hurwitz.
• Hypothesis H
2
: The inequality E
n−1
M
n−1
≤
E
n
M
n
is verified.
• Hypothesis H
3
: The graph of the scalar function
T (u) = g ◦ k
y
(u)
and that of its reciprocal function T
−1
(u) have a
unique intersection point on the open interval u ∈
(0, g
max
).
The scalar function k
y
(.) is the static input-output
characteristic associated to the monotone part of (1)
(resp. (2)), see Definition 2 in subsection 3.1.
Proposition 1. If H
1
, H
2
and H
3
are satisfied, then for
any x
1
and E
n
, the reversible end product structure (1)
has globally attractive equilibrium.
2.2 Irreversible Pathways
The main difference between the irreversible and the
reversible metabolic pathways is in the reaction rates
f
i
for the first and intermediate enzymes. Indeed, here
we assume that the reaction rates depend only on the
substrate concentration and have the following prop-
erties:
• For the first enzyme. We assume that the function
f
1
is increasing in its first argument and decreas-
ing in its second argument and for any x
1
> 0,
lim
x
n
→+∞
f
1
(x
1
, x
n
) = 0.
In addition, we have for any x
n
≥ 0, f
1
(0, x
n
) = 0
and there exists M
1
> 0 such that for any x
1
> 0
and x
n
≥ 0, f
1
(x
1
, x
n
) ∈ [0, M
1
).
• For the intermediate enzymes: f
i
i ∈ {2, . . . , n −1}
is strictly increasing in x
i
and f
i
(0) = 0. More-
over, there exists M
i
> 0 such that
lim
x
i
→+∞
f
i
(x
i
) = M
i
.
Then, the end product structure of the linear irre-
versible metabolic pathways is described by the fol-
lowing dynamical system











˙x
2
= E
1
f
1
(x
1
, x
n
) − E
2
f
2
(x
2
)
˙x
3
= E
2
f
2
(x
2
) − E
3
f
3
(x
3
)
.
.
.
.
.
.
.
.
.
.
.
.
˙x
n
= E
n−1
f
n−1
(x
n−1
) − E
n
f
n
(x
n
)
˙
E
1
= g(x
n
) − µE
1
.
(2)
Stability Results. Now, we state the contribution of
this paper concerning the global attractivity of the ir-
reversible metabolic pathway (2).
• Hypothesis H
4
: for each i ∈ {2, . . . , n} the in-
equality is verified E
1
M
1
≤ E
i
M
i
, where E
1
is the
upper bound of all solutions E
1
(t).
Proposition 2. The irreversible end product structure
(2) has globally attractive equilibrium for any x
1
and
E
n
if hypotheses H
3
and H
4
are satisfied.
To prove Proposition 1 and Proposition 2, we will
use the monotone control system theory, in particu-
lar the negative feedback theorem. Thus, we present
briefly this theory in the next section and then we give
the proofs in section 4.
3 MONOTONE CONTROL
SYSTEMS
Monotone control systems theory (Angeli and Son-
tag, 2003) is an extension of the autonomous mono-
tone system theory (Smith, 1995). Briefly, monotone
control system is a dynamical system on an ordered
metric space which has the property that ordered ini-
tial states and ordered inputs generate ordered state
trajectories and ordered outputs. In other words, a
controlled dynamical system (3),

˙
x(t) = f(x(t), u(t))
y(t) = h(x)
, x(t
0
) = cst, (3)
where x(t) ∈ X ⊆ R
n
and u(t) ∈ U ⊆ R
m
, is
said monotone if the following implication holds:
∀(x
1
(t
0
), x
2
(t
0
)) ∈ X
2
and ∀(u
1
(t), u
2
(t)) ∈ U
2
,
x
1
(t
0
)  x
2
(t
0
), u
1
(t)  u
2
(t) ⇒
x
1
(t, x
1
(t
0
), u
1
(t))  x
2
(t, x
2
(t
0
), u
2
(t)) ∀t > t
0
(4)
where x(t, x(t
0
), u(t)) represent the state trajectory
generated by (3) with x(t
0
) as initial state and u(t)
as input. The dimensions of the vectors x, u and y are
respectively n, m and p.
Here, we consider that  is the classical lower or
equal comparison operator ≤, applied component by
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
24

component. Systems that are monotone with respect
to this order are called cooperative systems, as all
state variables have a positive influence on one other
and the inputs act positively on state variables.
Proposition 3. The dynamical system (3) is coopera-
tive if and only if the following properties hold:
∂ f
i
∂x
j
(x, u) ≥ 0 ∀x ∈ X, ∀u ∈ U, ∀i 6= j
∂ f
i
∂u
j
(x, u) ≥ 0 ∀x ∈ X, ∀u ∈ U, ∀i, j
∂h
i
∂x
j
(x) ≥ 0 ∀x ∈ X, ∀i, j
(5)
Proof. See (Angeli and Sontag, 2003; Angeli and
Sontag, 2004).
After this brief recall about monotone control sys-
tems, we now introduce in the next the negative feed-
back theorem which states stability conditions for
monotone control systems with negative feedback.
3.1 Stability Analysis with Monotone
Control System
Recently, the negative feedback theorem of the mono-
tone control system theory is used to analyze stability
of several biological systems. Indeed, this theorem
allows, under some conditions, to obtain the globally
attractive stable steady state of non-monotone dynam-
ical systems. Here we give some definitions and as-
sumptions needed to state the negative feedback the-
orem.
Definition 1 (Angeli and Sontag, 2003). We say that
the SISO dynamical system (3) (m = p = 1) admits an
input to state static characteristic k
x
(.) : U → X if, for
each constant input u ∈ U, there exists a unique glob-
ally asymptotically stable equilibrium noted k
x
(u).
Definition 2 (Angeli and Sontag, 2003). SISO sys-
tem with an input-state characteristic and with a con-
tinuous output map y = h(x) has an input to out-
put characteristic defined as the composite function
k
y
(u) = (h ◦ k
x
)(u).
Note that, if the system (3) (with m = p = 1) is
cooperative and admits a static input-state character-
istic k
x
and static input-output characteristic k
y
, then
k
x
and k
y
must be increasing with respect to u, viz.
∀ (u
1
, u
2
) ∈ U
2
, u
1
≥ u
2
⇔ k
x
(u
1
) ≥ k
x
(u
2
),
k
y
(u
1
) ≥ k
y
(u
2
).
Assumptions. Consider the non-monotone au-
tonomous system given by (6)
˙
x(t) = F(x), (6)
and let us state the following assumptions,
• H
5
: Any state trajectory generated by system (6)
is bounded.
• H
6
: System (6) is decomposable into an open loop
SISO monotone control system (7)

˙
x(t) = f(x, u)
y(t) = h(x),
(7)
closed by a monotone decreasing feedback law
f
b
: y −→ u as depicted in Figure 2.
() ( , )
()
tu
yh
=
⎧
⎨
=
⎩
xfx
x

()
b
f
y
y
u
Figure 2: System (6) in closed loop configuration.
• H
7
: Open loop system (7) admits a well-defined
static input-output characteristic k
y
(.).
Then, we can introduce the negative feedback theo-
rem.
Theorem 1. Let (8) be a discrete scalar dynamical
system associated to the continuous non-monotone
system (6)
u
j+1
= ( f
b
◦ k
y
)(u
j
). (8)
If this iteration has a globally attractive fixed point u
∗
on an open interval U
x
, then the autonomous system
(6), provided that the assumptions H
5
, H
6
and H
7
are
satisfied, has a globally attracting steady state x
∗
=
k
x
(u
∗
).
Proof. See (Angeli and Sontag, 2003).
Hereafter, we give proofs of our main results
stated in subsections 2.1 and 2.2.
4 PROOF OF THE MAIN
RESULTS
In this section, we prove that propositions 1 and 2
are consequences of Theorem 1. We start with the
irreversible metabolic pathways, for which the static
input-state characteristic of its monotone part is eas-
ier to establish. Then we will focus on the reversible
pathways.
4.1 Irreversible Structure
In this subsection we will show that the technical
Proposition 2 is a consequence of Theorem 1.
STABILITY ANALYSIS FOR BACTERIAL LINEAR METABOLIC PATHWAYS WITH MONOTONE CONTROL
SYSTEM THEORY
25

Checking Assumption H
5
. First of all, let us prove
the boundedness of the controlled enzyme E
1
which
is governed by the following differential equation
˙
E
1
= g(x
n
) − µE
1
. (9)
By definition we know that g(.) is bounded, viz.
∀x
n
, g(x
n
) ∈ (0, g
max
]. Then, for any x
n
the solution
E
1
(t) of (9) is framed by
ˇ
E
1
(t) ≤ E
1
(t) ≤
ˆ
E
1
(t),
where
ˇ
E
1
(t) and
ˆ
E
1
(t) are respectively the solutions
of the following stable linear differential equations
˙
ˇ
E
1
= −µ
ˇ
E
1
and
˙
ˆ
E
1
= g
max
− µ
ˆ
E
1
.
Thus, there exists
E
1
> 0 | ∀t ≥ 0, E
1
(t) ≤ E
1
.
Now, consider the first differential equation of (2)
˙x
2
= E
1
f
1
(x
1
, x
n
) − E
2
f
2
(x
2
)
≤ E
1
M
1
− E
2
f
2
(x
2
).
We know that f
2
(.) is positive increasing and
bounded. Then if
E
1
M
1
≤ E
2
M
2
, (10)
there exists x
?
2
such that E
2
f
2
(x
?
2
) = E
1
M
1
, and we
obtain
∀x
2
> x
?
2
, ˙x
2
≤ 0,
namely the solution x
2
(t) decreases towards x
?
2
and
then the metabolite concentration x
2
is bounded. In
addition, for any initial condition x
2
(t
0
) there exists
t
?
≥ t
0
such that,
∀t ≥ t
?
, E
2
f
2
(x
2
(t)) ≤ E
2
f
2
(x
?
2
) = E
1
M
1
.
To proof the boundedness of the remainder metabolite
concentrations, we use mathematical induction. As-
sume that x
i
is bounded, viz. the following inequality
is satisfied
E
1
M
1
≤ E
i
M
i
, (11)
and there exists (t
?
, x
?
i
) such that for all t ≥ t
?
E
i
f
i
(x
i
(t)) ≤ E
i
f
i
(x
?
i
) = ·· · = E
2
f
2
(x
?
2
) = E
1
M
1
.
Then, for t ≥ t
?
the dynamics of the next metabolite
concentration x
i+1
is bounded by
˙x
i+1
= E
i
f
i
(x
i
) − E
i+1
f
i+1
(x
i+1
)
≤ E
i
f
i
(x
?
i
) − E
i+1
f
i+1
(x
i+1
)
= E
1
M
1
− E
i+1
f
i+1
(x
i+1
).
Hence we show, with the same way used to prove the
boundedness of x
2
, that inequality (12) guarantees the
boundedness of the metabolite concentration x
i+1
.
E
1
M
1
≤ E
i+1
M
i+1
. (12)
Therefore H
4
guarantees the boundedness of the all
state trajectories generated by (2), namely H
5
.
Checking Assumption H
6
. System (2) is not
monotone. However, we can regard it as a coopera-
tive controlled system (13), which has a triangular Ja-
cobian matrix DF(x) with nonnegative off-diagonal
entries, closed by a negative feedback (14),
• Open loop (cooperative system)















˙x
2
= E
1
f
1
(x
1
, g
−1
(u)) − E
2
f
2
(x
2
)
˙x
3
= E
2
f
2
(x
2
) − E
3
f
3
(x
3
)
.
.
.
.
.
.
.
.
.
.
.
.
˙x
n
= E
n−1
f
n−1
(x
n−1
) − E
n
f
n
(x
n
)
˙
E
1
= u − µE
1
y = x
n
(13)
• Negative feedback
u = g(y) (14)
where g
−1
(.) is the reciprocal function of g(.) and u ∈
(0, g
max
) since g(.) ∈ (0, g
max
]. This verifies H
6
.
Checking Assumption H
7
. The static input-state
characteristic k
x
(u) of (13) is computed at steady
states corresponding to constant inputs u. Thus, we
vanish all the time derivatives of (13) to obtain:
k
T
x
(u) =

f
−1
2

f
1
(
x
1
,g
−1
(u))u
E
2
µ

, . . . , f
−1
n

f
1
(x
1
,g
−1
(u))u
E
n
µ

,
u
µ

(15)
and for the static input-output characteristic we have:
k
y
(u) = f
−1
n

f
1
(x
1
, g
−1
(u))u
E
n
µ

(16)
Since functions f
i
(.), i = 2, . . . , n are bounded, the ex-
istence of (15) is conditioned by the following in-
equalities:
∀i, ∀u ∈ (0, g
max
),
f
1
(x
1
, g
−1
(u))u
E
i
µ
≤ M
i
which are always true if assumption H
4
is verified.
Moreover, as system (13) is cooperative, both static
characteristics ((15) and (16)) are increasing with re-
spect to u.
Now, to prove that for each constant input u ∈
(0, g
max
) there exists a unique globally asymptotically
stable equilibrium point k
x
(u) for (13), we consider
separately the dynamics of the enzymatic reactions
( ˙x
2
, . . . , ˙x
n
)
T
and that of the genetic regulation
˙
E
1
.
• The growth rate µ of the bacteria is constantly pos-
itive. Then for each constant input u all the so-
lutions generated by the dynamics of the genetic
regulation converge asymptotically to
u
µ
.
• The Jacobian matrix DF(x) of the dynamics of
the enzymatic reactions is a lower triangular ma-
trix with nonnegative off-diagonal entries and real
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
26

negative eigenvalues. Then −DF(x) is a M-
Matrix (Berman and Plemmons, 1994) and there
exists a diagonal matrix P = diag(p
1
, . . . , p
n
) with
p
i
> 0 such that
∃ε > 0, ∀x, PDF(x) + DF(x)
T
P < −εI
n−1
.
(17)
Consequently, we can state that the dynamics
of the enzymatic reactions have a well defined
quadratic Lyapunov function:
V (z) = z
T
Pz,
where z = x − x
∗
, x
∗
i
= (k
x
(u))
i
, i = 2, . . . , n and
˙
V (z) = z
T
P[f(x, u) − f(x
∗
, u)]
= z
T
R
1
0
PDF(λz + x)zdλ
=
1
2
z
T
R
1
0
(PDF(λz + x) + DF(λz + x)
T
P)dλz
≤ −
1
2
ε k z k
2
(18)
Hence, for each constant input u ∈ (0, g
max
), any so-
lution of the open loop system (13) converges asymp-
totically to the unique steady state given by (15). This
verifies assumption H
7
.
Now, to complete the proof that the Proposition
2 is consequence of Theorem 1, we will show that
assumption H
3
implies the global attractivity of the
following scalar discrete dynamical system
u
j+1
= g( f
−1
n
(
f
1
(
x
1
, g
−1
(u
j
))u
j
E
n
µ
)) (19)
To do so, (i) we prove existence and unicity of a fixed
point u
∗
for (19); and (ii) we give convenient condi-
tion which guarantee its global attractivity.
Existence and Unicity. To prove this property, it
is sufficient to show that the curves of the functions
g
−1
(u) and k
y
(u) have a unique intersection point over
the interval (0, g
max
). Since:
• k
y
(u) is is monotone increasing with respect to u
and for u = 0, k
y
(0) ≥ 0 and lim
u→g
max
k
y
(u) = +∞
• g
−1
(u) is monotone decreasing with respect to
u and lim
u→0
g
−1
(u) = +∞ and for u = g
max
,
g
−1
(g
max
) = 0,
then the two curves have a unique intersection point
u
∗
(see Figure 3) which present the unique fixed point
of (19).
Global Attractivity. Denote by T
2
the composite
function
T
2
(u) = (T ◦ T )(u),
where T (u) = (g ◦ k
y
)(u). The following proposition
gives the necessary and sufficient condition for the
global attractivity of the unique equilibrium of (19).
(.)
y
k
1
(.)g
−
y
u
max
g
*
u
Figure 3: Graphical proof of the existence and unicity of the
fixed point u
∗
for the discrete system (19).
Proposition 4. If u
∗
is also the unique fixed point of
T
2
(u) on (0, g
max
), That is
∀u ∈ (0, g
max
), T
2
(u) = u ⇔ u = u
∗
, (20)
then (19) converges to its unique fixed point.
Proof : see (Enciso and Sontag, 2006).
In practice, we can check condition (20) by graph-
ical test (H
3
). Indeed, if the graph of T (u) and
that of T
−1
(u) have a unique intersection point u
∗
over (0, g
max
), then the composite function T
2
(u) has
unique fixed point u
∗
. This completes the proof.
4.2 Reversible Structure
Now, consider the reversible metabolic pathways (1)
and we prove that Proposition 1 is a consequence of
Theorem 1.
Checking Assumption H
5
: First, note that the en-
zyme E
1
is bounded (see proof given in subsection
4.1). Now, to analyze the boundedness of all the
metabolite concentrations of (1), we proceed by step
and we show that if any metabolite concentration x
i
is bounded then the metabolite concentration x
i−1
is
also bounded. We start by x
2
, and we consider the
first differential equation of (1),
˙x
2
= E
1
f
1
(x
1
, x
2
, x
n
) − E
2
f
2
(x
2
, x
3
)
≤ E
1
f
1
(x
1
, x
2
, 0) − E
2
f
2
(x
2
, x
3
).
We assume that x
3
is bounded (∀t > 0, x
3
(t) ≤ x
3
),
then by definition there exists x
?
2
such that:
f
1
(x
1
, x
?
2
, 0) = 0 and f
2
(x
?
2
, x
3
) ≥ 0,
and thus at x
?
2
we obtain ˙x
2
≤ 0. Hence the threshold
x
?
2
is repulsive, and so we have proved that the bound-
edness of x
3
implies the boundedness of x
2
.
Now, for any metabolite concentration x
i
, i ∈
{3, . . . , n − 1} we have x
i−1
bounded with bound x
i−1
,
and we assume that x
i+1
is bounded with bound x
i+1
.
Then the dynamics of x
i
is bounded by:
˙x
i
= E
i−1
f
i−1
(x
i−1
, x
i
) − E
i
f
i
(x
i
, x
i+1
)
≤ E
i−1
f
i−1
(x
i−1
, x
i
) − E
i
f
i
(x
i
, x
i+1
),
STABILITY ANALYSIS FOR BACTERIAL LINEAR METABOLIC PATHWAYS WITH MONOTONE CONTROL
SYSTEM THEORY
27

and by definition we have
∃x
?
i
| f
i−1
(x
i−1
, x
?
i
) ≤ 0 and f
i
(x
?
i
, x
i+1
) ≥ 0.
Hence for x
?
i
we obtain ˙x
i
≤ 0, and so the thresh-
old x
?
i
is repulsive. Thus, we have proved that ∀i ∈
{2, . . . , n − 1} the boundedness of x
i+1
implies the
boundedness of x
i
. Lastly, consider the dynamics of
the concentration of the end product x
n
,
˙x
n
= E
n−1
f
n−1
(x
n−1
, x
n
) − E
n
f
n
(x
n
)
≤ E
n−1
M
n−1
− E
n
f
n
(x
n
).
Since f
n
(.) is positive increasing and bounded with
respect to x
n
, it is clear that if E
n−1
M
n−1
≤ E
n
M
n
we
obtain
∃x
n
| ∀x
n
≥ x
n
⇒ ˙x
n
≤ 0
independently of the values of x
n−1
. Consequently, if
H
2
is true, then all the state trajectories generated by
(1) are bounded and so assumption H
5
is verified.
Checking assumption H
6
: As in the case of the
irreversible metabolic pathways, structure (1) is not
monotone. Nevertheless, we can decompose it into an
open loop cooperative controlled system (21), which
has tridiagonal Jacobian matrix DF(x) with nonneg-
ative off-diagonal entries, closed by a negative feed-
back (22).
• Open loop (cooperative system)















˙x
2
= E
1
f
1
(x
1
, x
2
, g
−1
(u)) − E
2
f
2
(x
2
, x
3
)
˙x
3
= E
2
f
2
(x
2
, x
3
) − E
3
f
3
(x
3
, x
4
)
.
.
.
.
.
.
.
.
.
.
.
.
˙x
n
= E
n−1
f
n−1
(x
n−1
, x
n
) − E
n
f
n
(x
n
)
˙
E
1
= u − µE
1
y = x
n
(21)
• Negative feedback
u = g(y) (22)
where g
−1
(.) and g(.) are the same as in the irre-
versible case and also u ∈ (0, g
max
). Hence, assump-
tion H
6
is intrinsically satisfied.
Checking assumption H
7
: In the reversible con-
text, build the static input-state characteristic is not
explicit as in the irreversible case. However, to es-
tablish this characteristic we use the monotonicity
property of all reaction rates f
i
(., .), i ∈ {1, . . . , n}.
First, we show that at steady state there exists a bi-
nary relation between each metabolite concentration
x
i
, i ∈ {3, . . . , n} and x
2
. Second, we show that the
metabolite concentration x
2
is an increasing function
of the constant input u.
• Consider the dynamics corresponding to the last
pool X
n
. Since: (i) the function f
n
(x
n
) is mono-
tone increasing in x
n
with f
n
(0) = 0, (ii) the func-
tion f
n−1
(x
n−1
, x
n
) is decreasing in x
n
and (iii) for
any x
n−1
there exists x
∗
n
such that f
n−1
(x
n−1
, x
∗
n
) =
0,
∀x
n−1
, ∃x
n
| E
n−1
f
n−1
(x
n−1
, x
n
) = E
n
f
n
(x
n
).
In other words, we can say that there exists a
monotone increasing function H
n
(.) with respect
to x
n−1
such that:
x
n
= H
n
(x
n−1
). (23)
• According to the previous stage, we can write
f
n
(x
n
) = f
n
(H
n
(x
n−1
)).
Thus, since H
n
(.) is monotone increasing in x
n−1
,
f
n
(.) is also monotone increasing in x
n−1
. Now,
consider the dynamics of the pool X
n−1
. By
definition f
n−2
(x
n−2
, x
n−1
) is decreasing in x
n−1
and for any x
n−2
there exists x
∗
n−1
such that
f
n−2
(x
n−2
, x
∗
n−1
) = 0. Hence, we deduce: ∀x
n−2
,
∃x
n−1
| E
n−2
f
n−2
(x
n−2
, x
n−1
) = E
n
f
n
(H
n
(x
n−1
)).
Therefore, there exists a monotone increasing
function H
n−1
(.) with respect to x
n−2
such that:
x
n−1
= H
n−1
(x
n−2
) and x
n
= H
n
(H
n−1
(x
n−2
)). (24)
• Then we repeat this reasoning to obtain at steady
state the following relations between x
2
and all the
metabolic concentrations x
i
, i ∈ {3, . . . , n}:
x
3
= H
3
(x
2
)
x
4
= H
4
(H
3
(x
2
))
.
.
.
x
n
= H
n
(H
n−1
(. . . H
3
(x
2
) ))
(25)
where all H
i
are increasing functions.
• Lastly, the enzyme’s dynamics vanished while
E
1
=
u
µ
. Thus, it is possible to build at the
steady state a monotone relationship between
the concentration of the pool X
2
and the in-
put u. Indeed, as we have shown previ-
ously, (i) the monotone decreasing property of
the function
u
µ
f
1
(x
1
, x
2
, g
−1
(u)) in x
2
, (ii) the
monotone increasing property of the function
f
n
(H
n
(H
n−1
(. . . H
3
(x
2
) )) in x
2
, and (iii) the exis-
tence of x
∗
2
such that f
1
(x
1
, x
∗
2
, g
−1
(u)) = 0 allow
to state: ∀u, ∃x
2
such that,
u
µ
f
1
(x
1
, x
2
, g
−1
(u)) = f
n
(H
n
(H
n−1
(. . . H
3
(x
2
) ))
Then, at the steady state there exists a monotone
increasing function H
2
(.) with respect to u such
that:
x
2
= H
2
(u). (26)
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
28

Hence, the static input-state characteristic of the sys-
tem (21) is given by:
k
T
x
(u) =

H
2
(u), H
3
(H
2
(u)), . . . , H
n
(H
n−1
(. . . H
2
(u) )),
u
µ

(27)
and its input-output characteristic is obtained by the
composition law between (27) and the output equa-
tion of (21),
k
y
(u) = H
n
(H
n−1
(. . . H
2
(u) )). (28)
Now, we must prove that for each constant input
u the vector [x
∗T
,
u
µ
] = k
T
x
(u) is the globally asymp-
totically stable equilibrium point for the open loop
system (21). To do so, we use the same analysis
as in the irreversible case. First, we separate the
two dynamics (enzymatic reaction, genetic regula-
tion) and we deduce that for each constant input u
all the solutions generated by the dynamics of the ge-
netic regulation (
˙
E
1
) converge to
u
µ
. Second, hypoth-
esis H
1
claims the existence of Tridiagonal Hurwitz
matrix Q with nonnegative off-diagonal entries such
that for all x the Jacobian matrix DF(x) of the dynam-
ics of the enzymatic reactions ( ˙x
2
, . . . , ˙x
n
) is bounded
by, DF(x) ≤ Q. Then there exists a diagonal matrix
N = diag(n
1
, . . . , n
n
) with n
i
> 0 and a real number
ε > 0 such that ∀x
NDF(x) + DF
T
(x)N ≤ NQ + Q
T
N
≤ −εI
n−1
(29)
because −Q is a M-Matrix (Berman and Plemmons,
1994). Thus, the dynamics of the enzymatic reactions
admits as Lyapunov function the quadratic form
V (z) = z
T
Nz,
where z = x −x
∗
. See previous demonstration of (18).
Therefore, under assumption H
1
, relation (27) gives
the globally asymptotically stable steady state of the
open loop system (21) for each constant input u. This
verifies assumption H
7
.
Finally, as we have shown in the context of ir-
reversible metabolic pathways (here k
x
(.), k
y
(.) and
g
−1
(.) have the same properties with respect to u as
in the irreversible context), we can check the global
convergence of the following scalar discrete time dy-
namical system
u
j+1
= g(H
n
(H
n−1
(. . . H
2
(u
j
) )), (30)
to its unique fixed point u
∗
∈ (0, g
max
) by the same
graphical test stated in assumption (H
3
). This com-
pletes the proof that Proposition 1 is a consequence
of Theorem 1.
5 CONCLUSIONS
We have used in this paper the negative feedback the-
orem of monotone control SISO systems theory, to
give technical propositions which prove global attrac-
tivity of linear metabolic pathways. For future works,
we will consider the stability analysis for dynamical
systems through monotone control MIMO systems.
That will allow us to tackle the stability issue for com-
plex bacterial metabolic networks.
REFERENCES
Angeli, D. and Sontag, E. D. (2003). Monotone control
systems. IEEE transactions on automatic control,
48:1684–1698.
Angeli, D. and Sontag, E. D. (2004). Multi-stability in
monotone input/output systems. Systems and Control
Letters, 51:185–202.
Angeli, D. and Sontag, E. D. (2008). Oscillations in i/o
monotone systems under negative feedback. IEEE
transactions on automatic control, 55:166–176.
Arcak, M. and Sontag, E. D. (2006). Diagonal stability of
a class of cyclic systems and its connection with the
secant criterion. Automatica, 42:1531–1537.
Berman, A. and Plemmons, R. (1994). Nonnegative Matri-
ces in the Mathematical Sciences. Society for Indus-
trial and applied Mathematics, Philadelphia.
Enciso, G. A. and Sontag, E. D. (2006). Global attractiv-
ity, i/o monotone small-gain theorems, and biological
delay systems. Discrete and Continuous Dynamical
Systems, 14:549–578.
Goelzer, A., Bekkal-Brikci, F., Martin-Verstraete, I., Noirot,
P., Bessi
´
eres, P., Aymerich, S., and Fromion, V.
(2008). Reconstruction and analysis of the genetic
and metabolic regulatory networks of the central
metabolism of bacillus subtilis. BMC Systems Biol-
ogy, doi:10.1186/1752-0509-2-20.
Gollnick, P., Babitzke, P., Antson, A., and CA, C. (2005).
Complexity in regulation of tryptophan biosynthesis
in bacillus subtilis. Annual review of genetics, 39:47–
68.
Grundy, F., Lehman, S., and Henkin, T. (2003). The l
box regulon: lysine sensing by leader rnas of bacte-
rial lysine biosynthesis genes. PNAS, 100(21):12057–
12062.
Sanchez, L. (2009). Global asymptotic stability of the good-
win system with repression. Nonlinear analysis : real
world applications, 10(4):2151–2156.
Smith, H. L. (1995). Monotone dynamical systems: An In-
troduction to the theory of competitive and coopera-
tive systems. Mathematical Surveys and Monographs
Vol. 41, AMS, Providence, RI.
Tyson, J. and Othmer, H. (1978). The dynamics of feedback
control circuits in biological pathways. In R. Rosen,
and F.M. Snell (Eds.), Progress in theoretical biology
(Vol. 5), pages 1–62, New York: Academic Press.
Wang, L., de Leenheer, P., and Sontag, E. (2008). Global
stability for monotone tridiagonal systems with nega-
tive feedback. In Proc. IEEE Conf. Decision and Con-
trol CDC, pages 4091–4096, Cancun,Mexico.
STABILITY ANALYSIS FOR BACTERIAL LINEAR METABOLIC PATHWAYS WITH MONOTONE CONTROL
SYSTEM THEORY
29