A SPATIAL ONTOLOGY FOR HUMAN-ROBOT INTERACTION
Lamia Belouaer, Maroua Bouzid and Abdel-Illah Mouaddib
Universit
´
e de Caen - UFR des Sciences, D
´
epartement d’Informatique
Campus C
ˆ
ote de Nacre, Bd Mar
´
echal Juin, BP 5186, 14032 Caen Cedex, France
Keywords:
Spatial Representation and Reasoning, Spatial Relations, Ontology, Planning, Human-robot Interaction.
Abstract:
Robotics quickly evolved in the recent years. This development widened the intervention fields of robots.
Robots interact with humans in order to serve them. Improving the quality of this interaction requires to
endow robots with spatial representation and/or reasoning system. Many works have been dedicated to this
purpose. Most of them take into account metric, symbolic spatial relationships. However, they do not consider
fuzzy relations given by linguistic variables in humans language in human-robot interaction. These relations
are not understood by robots. Our objective is to combine human representation (symbolic, fuzzy) of space
with the robot’s one to develop a mixed reasoning. More precisely, we propose an ontology to manage both
spatial relations (topological, metric), fuzziness in spatial representation. This ontology allows a hierarchical
organization of space which is naturally manageable by humans and easily understandable by robots. Our
ontology will be incorporated into a planner by extending the planning language PDDL.
1 INTRODUCTION
Robotics quickly evolved in the last decade and there
is an increasing demand for intelligent systems like
robots that can help in daily life. This development
widened the intervention fields of robots such as a
public area where robots interact with humans in or-
der to serve them. To improve the quality of this in-
teraction, robots should behave as much as possible
like humans. This requires to endow robots with rep-
resentations and/or systems of reasoning directly in-
spired by humans. We focus on human-robot interac-
tion (HRI) based on spatial organization of observed
structures, in order to plan robots actions.
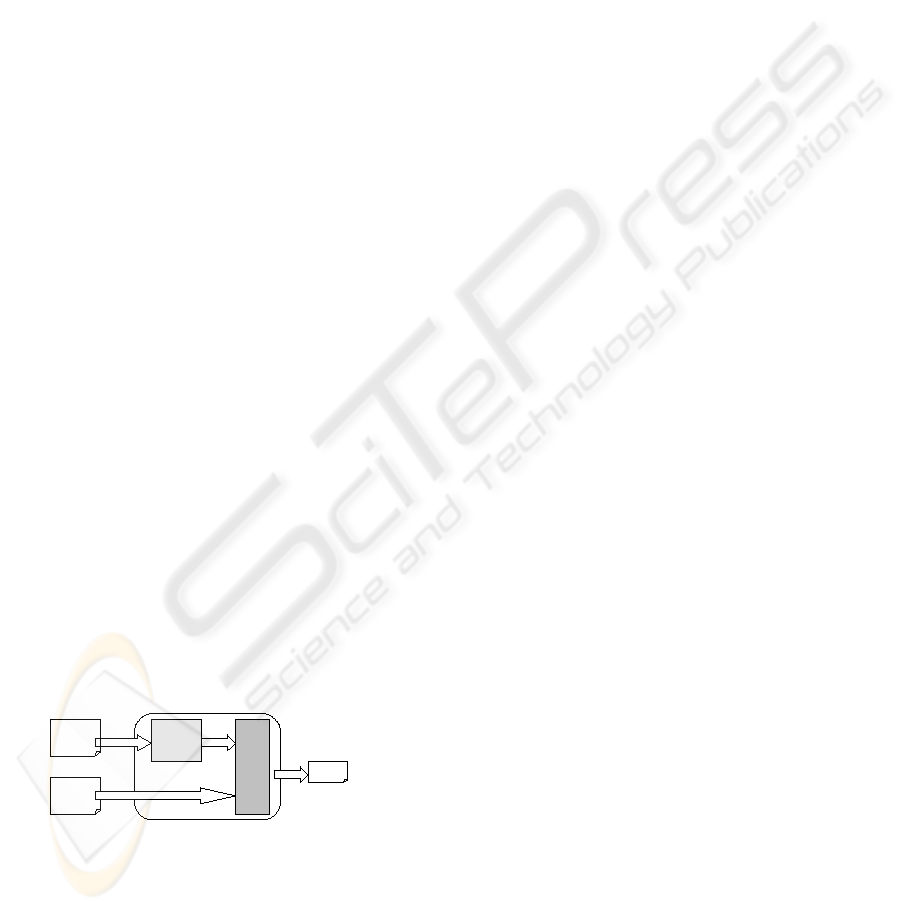
Planner
Spaceontology
Problem :
initial state
goals
Spatial
information
Plan
Figure 1: Spatial Planner.
Our goal is to develop a planner allowing to
solve problems taking into account spatial informa-
tion. This planner, called Spatial Planner (Fig. 1),
consists of two sub-systems. The first sub-system,
SpaceOntology allows a spatial representation and
reasoning model. As input, it takes a set of impre-
cise and incomplete spatial information. However,
as output, it provides a structured knowledge about
the environment to explored in planning. The second
sub-system, Planner, defines the set of actions to be
executed by the robot in order to achieve its mission.
In this paper, we focus on SpaceOntology that
models spatial representation and reasoning for better
mediation between humans and robots. This ontology
concerns:
• Hierarchical representation of space. The space
is structured to be manageable by humans and
robots.
• Numerical/Symbolic representation of space.
From the human’s point of view, the space is gen-
erally considered in a symbolic way (in, disjoint,
north, close, . . . ). From the robot’s point of view,
the space is considered in numerical way (angles,
distances, . . . ).
SpaceOntology gives a description of the environ-
ment (hierarchical organization, spatial relations) un-
derstandable by both humans and robots.
This paper is organized as follows. In section 2,
we place our work with regard to the state of art of the
spatial representation and ontologies. In section 3, we
present our framework to model spatial representation
and reasoning. In section 4, we present SpaceOntol-
ogy. In section 5, we present how we use ontology to
develop a mixed reasoning (from human to robot and
154
Belouaer L., Bouzid M. and Mouaddib A. (2010).
A SPATIAL ONTOLOGY FOR HUMAN-ROBOT INTERACTION.
In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 154-159
DOI: 10.5220/0002948001540159
Copyright
c
SciTePress

from robot to human). In conclusion, we present our
future works.
2 RELATED WORK
2.1 Spatial Relations
The spatial relations have been developed in many do-
mains (image processing (Bloch and Ralescu, 2003),
GIS (Casati et al., 1998), . . . ). They can be di-
vided into topological, directional and distance rela-
tions (Kuipers and Levitt, 1988). In this paper, we
consider all these relations.
In robotics, quantitative representations of spatial
relations are commonly applied. Purely quantitative
representations have limitations particularly when im-
precise knowledge use spatial relations expressed in
linguistic terms, particular in HRI. Imprecision has to
be taken into account in such problems. It is often
inherent to human language. It may be caused by im-
precision about the objects to recognize due to the ab-
sence of crisp contours or by the imprecise semantics
of some relationships (eg. quite far, . . . ), or else by a
kind of task we would like fulfill in HRI. For exam-
ple, we may want a robot go towards a person while
remaining at security distance of it.
Our objective is to combine all symbolic represen-
tation with robotic numeric representation to develop
a mixed reasoning.
2.2 Ontologies and Spatial Dimension
Different techniques of spatial representation and rea-
soning have been proposed. Most are based on con-
straints, logical and algebraic approaches (Balbiani
et al., 1999). However, these approaches can not man-
age quantitative, qualitative and imprecise knowledge
at the same time. In HRI, we need to combine this
knowledge. For this reason, we must use an unified
framework to cover large classes of problems and po-
tential applications, and able to give rise to instanti-
ation adapted to each particular application. Ontolo-
gies (Gruber et al., 1995) appear as an appropriate tool
toward this aim.
Spatial ontologies can be found in some fields
such as GIS (Casati et al., 1998), Virtual Reality (Da-
siopoulou et al., 2005), Robotics (Dominey et al.,
2004), . . . All these ontologies are focused on the rep-
resentation of spatial concepts according to the ap-
plication domains. A major weakness of usual onto-
logical technologies is their inability to represent and
to reason with imprecision. An interesting work pre-
sented in (Hudelot et al., 2008) overcome this limit.
3 OUR FRAMEWORK
In our work, we set up an ontology to manage both
spatial relations, fuzziness in spatial representation.
Moreover, our ontology allows an organization of
space naturally manageable by human and easily un-
derstandable by the robot: hierarchical representation
of space.
3.1 Hierarchical Organization of Space
Hierarchical organization of space reduces the
amount of information considered for coping with a
complex, high-detailed world: concepts are grouped
into more general ones and these are considered new
concepts that can be abstracted again. The result is
a hierarchy of abstractions (or specialization) or a hi-
erarchy of concepts that ends when all information is
modeled by a single universal concept (or we reach
a desired level of specialization). Thus, we consider
this hierarchy to describe the considered space.
Our organization is made from the highest abstrac-
tion level to lowest (most detailed one) unlike the or-
ganization described in (Fern
´
andez-Madrigal et al.,
2004). The highest level represents the environment
with the maximum amount of detail available. The
lowest level represents the environment by a single
concept. Hierarchical representation of space allows
us to represent this space in a structure easily man-
ageable by human and robot. In addition, it provides
better performance than flat representation in naviga-
tion or path planning.
3.1.1 Spatial Entity
All concepts in spatial representation are called Spa-
tial Entities. A spatial entity is localizable in a given
space by one of its attributes or by geometric trans-
formation. From a geometric point of view, a spatial
entity ε is defined by a rectangle rect
ε
corresponding
to its axis-aligned bounding rectangles.
From hierarchical organization of space, derives
two categories of spatial entities. Space represents a
global space. This entity is the highest abstraction and
the lowest level in the hierarchy organization. Region
represents any spatial entity belonging to different hi-
erarchical levels (intermediate and final). A region is
a sub-space included in the given space. A region is
itself considered as a space that can be decomposed
into different sub-regions.
3.2 Spatial Relations
A spatial relation requires a reference frame. For ex-
ample, the relation bench is in front of coffee machine.
A SPATIAL ONTOLOGY FOR HUMAN-ROBOT INTERACTION
155

The semantic of the relation is not the same depend-
ing on whether the reference system is the coffee ma-
chine itself or an external observer. In order to have
an unique meaning and to remove the ambiguity, three
concepts have to be specified : the target object, the
reference object and the reference system (Hudelot,
2005). In our work, we consider both Intrinsic and
Egocentric reference frame.
3.2.1 Topological Relationships
We consider the ALBR relations defined in ABLR
(Above Below West Right) (Laborie et al., 2006).
This algebra balances between expressiveness and the
number of relations (reasoning/complexity). ABLR
reduces the number of relations while preserving the
directionality property of the representation defined
in (Allen, 1983). A topological relation is an ABLR
relation. This relation is a couple hr
X
, r
Y
i, where;
r
X
∈ {Le f t(L), OverlapsLe f t(O
L
),Contains(C
x
),
Inside(I
x
), OverlapsRightO
R
, Right(R)}
and
r
Y
∈ {Above(A), OverlapsAbove(O
A
),Contains(C
y
),
Inside(I
y
), Overl pasBelow(O
B
), Below(B)}.
3.2.2 Metrical Relationships
Metrical relations concern distance and orientation re-
lations (Bloch, 2005). We consider a 2D representa-
tion of the space given by (O,
−→
i ,
−→
j ). The origin O
is a reference system that can be intrinsic or egocen-
tric. In the following, a rectangle denotd ε represents
a spatial entity. Its symmetry center will be known as
the spatial entity name. P
x
(ε) (resp. P
y
(ε)) denotes
the projection of ε on (
−→
i ) axis (resp. (
−→
j ) axis).
In HRI under spatial constraints, fuzzy informa-
tion is a key point as said in section 2. In this work,
vagueness and ambiguity concern the vagueness of
the relationship itself. Indeed, we don’t need to eval-
uate if a spatial entity is in north of a referent spatial
entity since spatial entities are crisp. The application
of fuzzy approach mainly concerns the distance rela-
tionship. The aim is to find a way to represent the
symbolic direction and distance relationship (based
on linguistic variables) by a numerical direction and
distance and vice versa.
Directional Relationships. We describe directional
relations through cardinal direction : West of, North
of, East of and South of. We associate for every se-
mantic direction semantic West of, East of, North of
and South of following respective functions West
R
,
East
R
, North
R
(R is a referent object) and South
R
.
West
R
(ε) denotes ε is left of R given by West
R
(ε) =
{P
x
(ε) − P
x
(R) 6 0}. East
R
(ε) denotes ε is right of R
given by East
R
(ε) = {P
x
(ε) −P
x
(R) > 0}. North
R
(ε)
denotes ε is in north of R given by North
R
(ε) =
{P
y
(ε) − P
y
(R) > 0}. South
R
(ε) denotes ε is in south
of R given by South
R
(ε) = {P
y
(ε) −P
y
(R) 6 0}.
The representation of the 8 cardinal relationships
is possible by combining these four functions. Con-
sider the example of the directional relation the bench
b is north and east of coffee machine c
m
. This
corresponds to the combination of North
c
m
(b) and
East
c
m
(b):
North
c
m
(b) ⊕ East
c
m
(b) =
P
x
(b) − P
x
(c
m
) > 0
P
y
(b) − P
y
(c
m
) > 0
(1)
This representation allows us to express other direc-
tional relations (at the same level, between, . . . ).
Distance Relationships. We consider four linguis-
tic variables to describe distance relations: close to,
close to enough, far from enough, far from. We note
d(ε, r) in R
+
the euclidean distance between the point
of symmetry of two rectangles representing two re-
gions (r referent object and ε target object). The aim
is to find a way to represent the four linguistic vari-
ables already defined to evaluate distance by a nu-
meric value to evaluate it. To do so, we consider two
degrees, defined in (Schockaert, 2008), N
(α,β)
(p, q)
( 2) and F
(α,β)
(p, q) ( 3). The degree N represents
two points p and q are near each other and the de-
gree F represents how p is far from q (α, β > 0). We
have defined a hierarchical space organization. This
has an impact on the distance evaluation. Indeed, the
distance of 2m in a city is considered as near, how-
ever, 2m in an office is considered as far. From these
information, we define for each hierarchical level an
α and a β depending on the scale of this level.
N
(α,β)
(p, q) =
1 if d(p,q) ≤ α
0 if d(p,q) ≥ α +β
α+β−d(p,q)
β
otherwise β 6= 0
(2)
F
(α,β)
(p, q) =
1 if d(p,q) > α +β
0 if d(p,q) ≤ α
d(p,q)−α
β
otherwise β 6= 0
(3)
0
1
d(p,q)
N
,
p , q
F
,
p , q
Figure 2: Graphical representation of relationship between
N
(α,β)
(p, q) and F
(α,β)
(p, q).
From equations 2 and 3 and organization given in
figure 2, it is easy to deduce that: (1) if d ∈ [0, α] then
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
156
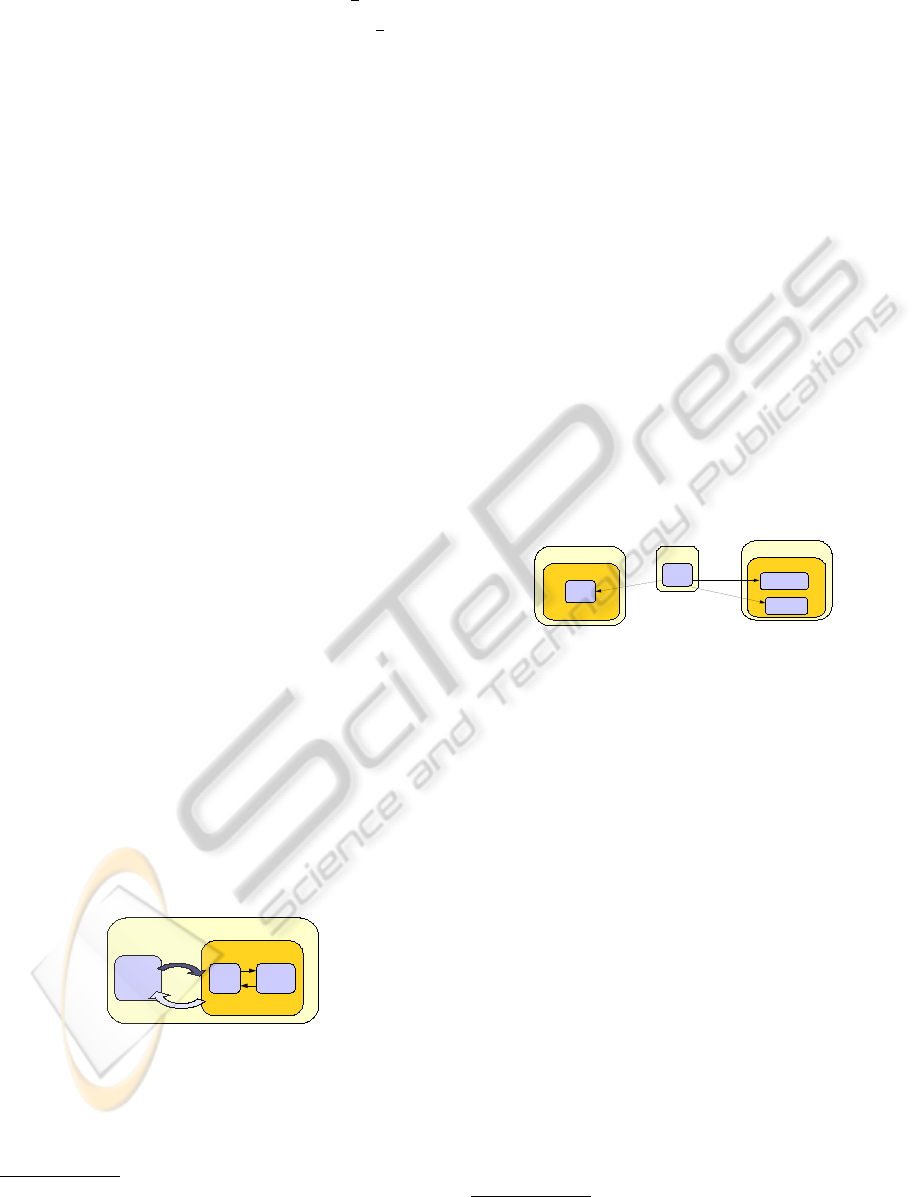
d is considered as close, (2) if d ∈]α, α +
β
2
] then d
is considered as close enough, (3) if d ∈]α +
β
2
, α +
β] then d is considered as far enough, (4) if d ∈]α +
β, +∞[ then d is considered as far.
4 IMPLEMENTATION
As a formal language, we opted for OWL DL formal-
ism (McGuinness et al., 2004; Baader et al., 2003).
This formalism benefits from the compactness and
expressiveness of DL. Indeed, an important charac-
teristic of DL is their reasoning capabilities of in-
ferring implicit knowledge from the explicitly repre-
sented knowledge. In this section, we describe how
we present and reason about spatial knowledge.
4.1 Spatial Entities as Concepts
One of important concepts of SpaceOntology is the
concept Space (Spacev T) (T for Thing
1
). This con-
cept represents a global environment (i.e a country, a
city, . . . ). Also, we define a concept Regions. This
concept is a subclass of concept Space (Regionsv
Space). Thus, we can consider the hierarchical defi-
nition of space. Indeed, a region itself is a space in the
next hierarchical level. Furthermore, the hierarchical
relationship between concepts Space and Regions is
given by subsumption. We offer the following links
consistsOf and isPartOf. The link consistsOf can ex-
press that space consists of one or more regions. The
link isPartOf can express one region may belong to
one or more spaces. These relationships are symmet-
rical and transitive.
Space v T u ∃ consistsOf.Regions u > 1
consistsOf
Regions v Space u ∃ isPartOf.Space u > 1
consistsOf
Space
building
Regions
region1 region11
1
2
3
4
Figure 3: Links between concepts and their instantiation.
From these links and their properties, we can com-
pose relationships between these two concepts. For
instance, the composite (2) relationship in figure 3, is
1
Thing is an OWL class that represents the set contain-
ing all individuals. Because of this all classes are subclasses
of OWL:Thing.
derived from the transitive links isPartOf (4) between
region1
1
with region1 and region1 with building.
Through this relationship we can deduce that region1
1
is part of the building.
4.2 Spatial Relations as Concepts
A spatial relation is not considered in our ontology
as a property between two regions but as a concept
on its own; SpatialRelations(SpatialRelationsv
T). This concept represents a set of all spatial rela-
tions between two regions. A SpatialRelations sub-
sumes TopologicalRelations and MetricRelations
which itself subsumes DirectionalRelations and Dis-
tanceRelations which itself subsumes DistanceAc-
cordingToActions and DistanceAccordingToHier-
archicalLevel.
4.2.1 HasRelation Concept
To define a spatial relationship between two regions
describing a given configuration, we need to link
these regions with a spatial relationship.
SpatialRelations
DirectionalRelations
Left_Of
HasRelation
relation1
Space
Regions
Coffe machine
office
concernsSpatialRelation
hasReferent
hasTarget
Figure 4: Links between concepts and their instantiation.
As already defined, a spatial relationship is given
by the concept SpatialRelations. We define the link
HasRelation as a concept which refers to the set of
spatial relations for which target and reference entities
are defined. This concept is useful to describe spatial
configurations.
HasRelation v T u ∃
concernsSpatialRelation.SpatialRelations u = 1
concernsSpatialRelation u ∃
hasReferent.Regions u > 1 hasReferent u ∃
hasTarget.Regions u = 1 hasTarget
Consider as an example that human asks the
robot to enter into ”the office left of the coffee ma-
chine”. In SpaceOntology, this expression is for-
malized as follows. First, identify this expression
by relation1. We note relation1:HasRelation
2
.
We consider that relation1 is an instantiation of
the concept HasRelation. Left
o f
is an instantia-
tion of the concept DirectionalRelations according
to a defined reference system for spatial relations
(Left
o f
:DirectionalRelations). The office and
2
These symbols are defined in description logics syntax
and interpretation
A SPATIAL ONTOLOGY FOR HUMAN-ROBOT INTERACTION
157

the coffee machine are instantiations of the concept
Regions (office:Regions and coffee:Regions).
5 OPERATING SPACEONTOLOGY
In this section, we present the exploitation of our on-
tology and the methods for reasoning. As already
mentioned, we developed an ontology to provide a ba-
sis spatial data to be used after in planning problems
to improve HRI. Exploitation of ontology is neces-
sary for path planning between two positions. In this
paper, we present how and by which methods from
ontology we can extract the paths between two posi-
tions even if the information is incomplete. Work on
path planing is the subject of future work.
5.1 Example
Consider an HRI problem in a building. A human
asks the robot to fetch a bottle near the coffee ma-
chine located in the hallway of the third floor. Then,
to bring back the bottle to the human who is on the
first floor (initial robot position’s). Specifically, robot
should compute the path between its position and bot-
tle position’s, catching the bottle and after to give it to
human. To explain the reasoning, we consider in the
following only the first part of the task, namely; fetch-
ing the bottle.
5.2 Reasoning
In SpaceOntology, we insisted on two key notions:
hierarchy of space and spatial relationships. Thus, we
rely on these notions for reasoning.
Consider the example given in section 5.1. By
giving a map with all the corridors and all access,
defining a path by considering the size of the map be-
comes quickly expensive. Hierarchical organization
of space simplifies the path computation. Indeed, it
helps to decompose the problem into 3 sub-problems:
(1) from initial position reach an access point to the
third floor, (2) from this access point plan to reach the
third floor and (3) from arrival position on the third
floor, plan to reach the coffee machine.
Reasoning for the first and last steps requires more
detailed information than the second step. For this
step, we must ignore the details given in two other
steps. However, considering floors like black boxes
does not guarantee the path quality. Consider that
quality is related to speed. Passing through certain
corridors with big distances can be faster than through
the ones with short distances but with many obstacles.
Thus, hierarchical organization of a space, involves
reasoning at each level.
Thus, we can construct a path between any two
given locations in an accurate (i.e in room number 3)
or approximate ( i.e somewhere on the first floor). In
this paper, we do not present an algorithm for find-
ing paths, but rather we present a structure generated
from the ontology providing a set of possible paths
between two positions by considering the space hier-
archy. For the target object, in our case the bottle, we
define the concept of target zone. Considering the hi-
erarchy of the environment, we define the target zone
as T
l
Z
(o), where l is the hierarchy level and o the ob-
ject or region targeted. Thus, we can deduce from
SpaceOntology a hierarchy for the target zone. This
allows us to determine the most abstract target zone
(T
0
Z
(o) = building) and the more detailed one (T
3
Z
(o)=
region of coffee machine).
Another key knowledge in this work are spatial re-
lationships. They allow, given an environment, to de-
scribe its spatial configuration (obstacle position’s).
For instance, we can describe that the corridor H is
adjacent to the door doorB of the office B. Here, an
example from SpaceOntology.owl allowing to illus-
trate the example.
<HasRelationWithIntersection rdf:ID="relation3">
<intersectionresult>
<Regions rdf:ID="doorB"/>
</intersectionresult>
<hasTarget>
<Regions rdf:ID="corriderH"/>
</hasTarget>
<hasReferent>
<Regions rdf:ID="officeB"/>
</hasReferent>
<concernsSpatialRelation>
<TopologicalRelations rdf:ID="leftinside">
<isahRelation rdf:resource="#Horiz_L"/>
<isavRelation rdf:resource="#Ver_Iy"/>
</TopologicalRelations>
</concernsSpatialRelation>
</HasRelationWithIntersection>
As already mentioned, our strategy of searching a
path is to find a path divided into different portions.
Each part belongs to a single hierarchical level. To
do this, we need a structure for this type of dedicated
research. This structure is generated from SpaceOn-
tology. Thus, we define the Crossing Network Graph.
5.2.1 Crossing Network Graph
A Crossing Network Graph(Γ
G
) is a directed graph.
A node in this graph represents a network of passage.
The nodes are organised hierarchically. The arcs rep-
resent relationships between nodes as described in
SpaceOntology.
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
158

A Crossing Network(Γ) is a graph whose nodes
are Crossing Network. Edges represent spatial ad-
jacency relations between two nodes described in
SpaceOntology giving a contact point between these
nodes, known as gateways. A gateway (i.e door, pass-
ing lane, . . . ) allows transitions between adjacent
spaces and between spaces adjacent in different hier-
archical levels. Edges are labeled by a couple (pass,
dist), where pass gives the gateway connecting these
regions (or networks) and dist is the distance sep-
arating these regions (or networks) passing through
this gateway. There are two types of crossing net-
works: (1) Low-level crossing Networks are crossing
networks whose nodes are crossing networks. It used
such a network mainly as we have not reached the
level of specialization wanted (or fixed). (2) High-
level crossing Networks are crossing networks whose
nodes are the regions. It used when level of special-
ization desired (or fixed) is reached.
The construction of Crossing Network Graph is
done from the abstract level to fixed detailed level.
First, we consider the target zone of the most abstract
level. In the same way, we consider the initial zone
of the most abstract level in the ontology. We select
the most abstract target zone and initial zone targeted
areas as these two zones are included in the same re-
gion. For instance, we consider the third floor (target
zone) and the first floor (initial). It requires setting
different gateways allowed to exit the initial zone and
enter to the target zone. From the spatial relationships
of adjacency defined SpaceOntology, we can find with
backward mechanism all possible paths to reach the
initial region.
6 CONCLUSIONS
This paper presents a spatial representation using an
ontology allowing us to represent and reason on spa-
tial objects represented from different point of views
(human and robot). Future work will concern to in-
tegrate it in planning by extending the planning lan-
guage PDDL. This is an innovative concept. In this
paper, several aspects are still cause for thought as the
assessment of a relationship without a fixed target or
the implementation of an algorithm to generate a path
according to some optimality criteria. These points
will be the subject of future work.
REFERENCES
Allen, J. (1983). Maintaining knowledge about temporal
intervals.
Baader, F., Calvanese, D., McGuinness, D., Patel-
Schneider, P., and Nardi, D. (2003). The description
logic handbook: theory, implementation, and applica-
tions. Cambridge Univ Pr.
Balbiani, P., Condotta, J.-F., and del Cerro, L. F. (1999).
A new tractable subclass of the rectangle algebra. In
IJCAI, pages 442–447.
Bloch, I. (2005). Fuzzy spatial relationships for image pro-
cessing and interpretation: a review. Image and Vision
Computing, 23:89–110.
Bloch, I. and Ralescu, A. (2003). Directional relative posi-
tion between objects in image processing: a compari-
son between fuzzy approaches. Pattern Recognition.
Casati, R., Smith, B., and Varzi, A. (1998). Ontological
tools for geographic representation. (FOIS’98).
Dasiopoulou, S., Mezaris, V., Kompatsiaris, I., Papastathis,
V., and Strintzis, M. (2005). Knowledge-assisted se-
mantic video object detection. IEEE Transactions on
Circuits and Systems for Video Technology.
Dominey, P., Boucher, J., and Inui, T. (2004). Building
an adaptive spoken language interface for perceptu-
ally grounded human–robot interaction. In Proceed-
ings of the IEEE-RAS/RSJ international conference on
humanoid robots.
Fern
´
andez-Madrigal, J., Galindo, C., and Gonz
´
alez, J.
(2004). Assistive navigation of a robotic wheelchair
using a multihierarchical model of the environment.
Integrated Computer-Aided Engineering.
Gruber, T. et al. (1995). Toward principles for the design of
ontologies used for knowledge sharing. International
Journal of Human Computer Studies.
Hudelot, C. (2005). Towards a cognitive vision platform
for semantic image interpretation; application to the
recognition of biological organisms.
Hudelot, C., Atif, J., and Bloch, I. (2008). Fuzzy spatial
relation ontology for image interpretation. Fuzzy Sets
and Systems.
Kuipers, B. (2000). The spatial semantic hierarchy. Artifi-
cial Intelligence, 119:191–233.
Kuipers, B. and Levitt, T. (1988). Navigation and mapping
in large scale space. AI magazine, 9:25.
Laborie, S., Euzenat, J., and Layaıda, N. (2006). A spatial
algebra for multimedia document adaptation. SMAT.
McGuinness, D., Van Harmelen, F., et al. (2004). OWL web
ontology language overview. W3C recommendation.
Schockaert, S. (2008). Reasoning about fuzzy temporal and
spatial information from the web. PhD thesis, Ghent
University, 2008.
A SPATIAL ONTOLOGY FOR HUMAN-ROBOT INTERACTION
159
