HIGHLY INTEGRATED LOW PRESSURE FLUID SERVO-VALVE

FOR APPLICATIONS IN WEARABLE ROBOTIC SYSTEMS

Michele Folgheraiter, Mathias Jordan, Luis M. Vaca Benitez, Felix Grimminger, Steffen Schmidt

Jan Albiez and Frank Kirchner

German Research Center for Artiﬁcial Intelligence (DFKI), Robotics Innovation Center

Robert-Hooke-Strasse 5D-28359 Bremen, Germany

Keywords:

Proportional Valve, Hydraulic Valve, Pneumatic Valve, Mechatronics, Pressure Control, Servo-Mechanism.

Abstract:

In this paper an innovative low pressure servo-valve is presented. The device was designed with the main

aim to be easily integrable into complex hydraulic/pneumatic actuation systems, and to operate at relatively

low pressure (< 50 · 10

Pa). Characteristics like compactness, lightweight, high bandwidth, and autonomous

sensory capability, where considered during the design process in order to achieve a device that fulﬁlls the

basic requirements for a wearable robotic system. Preliminary results about the prototype performances are

presented here, in particular its dynamic behavior was measured for different working conditions, and a non-

linear model identiﬁed using a recursive Hammerstein-Wiener parameter adaptation algorithm.

1 INTRODUCTION

State of the art robots that are actuated with a hy-

draulic system are generally thought to operate with

pressures greater than 200 · 10

Pa (Hayward, 1994),

(Jacobsen et al., 1991). This is mainly due to the fact

that it is convenient to increase the force/weight ra-

tio of the actuation system by increasing its opera-

tional pressure (Yoshinada et al., 1992). If from one

side increasing the pressure brings advantages, from

the other could represent a limitation. At ﬁrst the hy-

draulic components need to be designed to resist the

high forces generated by the ﬂuid pressure; this re-

quires therefore to employ thick and heavy materials

for pipes and actuators. Secondly, the usage of high

pressure could also cause a dangerous situation for the

operators that are in the proximity of the robot. The

safety issue is even more critical if the robot, in our

case an exoskeleton, is strictly coupled with the hu-

man being (Pons, 2008). Any failure in the hydraulic

system could seriously harm the user.

One of the main goal of VI-Bot project, un-

der development at DFKI Bremen (Robotics Innova-

tion Center), is to design an intrinsically safe, wear-

able arm exoskeleton for Tele-Robotics applications

(Folgheraiter et al., 2008; Folgheraiter et al., 2009a;

Folgheraiter et al., 2009b; Folgheraiter et al., 2009c).

As requirements the haptic interface should: enable

the operator to control complex robotics systems in

an intuitive way, implement a multi-points haptic

feedback to increase the immersion into the work

scenario, be light weight and adaptable to different

users, and integrate different levels of safe mecha-

nisms. Furthermore, the kinematics architecture of

the system should be designed in order to constrain

as less as possible the natural arm movements and its

workspace.

To achieve these goals and at the same time to

reduce the complexity of the system (number of re-

quired DOF), it is necessary to keep the exoskele-

ton’s joints near to the human arm, “ideally over-

lap them with the human articulations” in order to

avoid parallel kinematic loops. It turns out that

the necessity to have a compact, light, highly dy-

namic actuation system here is crucial. The ad-

vantages of using hydraulically actuators to oper-

ate the exoskeleton’s joints, if directly compared

with classical DC motors, are represented by their

high force/weight ratio, the possibility to use the

axes of the actuator as rotational/prismatic axes

of the robotic system, and their back-drivability.

Furthermore with a proper hydraulic supply and

a precise ﬂuid regulation, strength and high dy-

namic range can be achieved (Raibert et al., 2008),

Folgheraiter M., Jordan M., Benitez L., Grimminger F., Schmidt S., Albiez J. and Kirchner F. (2010).

A HIGHLY INTEGRATED LOW PRESSURE FLUID SERVO-VALVE FOR APPLICATIONS IN WEARABLE ROBOTIC SYSTEMS.

In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 72-78

DOI: 10.5220/0002948700720078

 SciTePress

(Kazerooni et al., 2006),(Kahn, 1969).

In ﬁgure 1 is shown the actual version of our hap-

tic interface. In total there are 7 actuated joints: 5

located in the shoulder/upper-arm and 2 in the fore-

arm. An additional passive joint allows the wrist

supination-pronation. All active joints are hydraulic

actuated, valves, sensors and electronics are thought

to be mounted directly in proximity of the actuators,

this in order to reduce the amount of cables and pipes

needed. The hydraulic pump and the primary power

supply are located outside the exoskeleton to avoid

additional weight to the system.

Figure 1: The arm exoskeleton equipped with 8 hydraulic

rotative and linear actuators.

A central element within the hydraulic system is

represented by the proportional servo-valve. On the

market there are plenty of proportional (4/3) hydraulic

valves, the problem is that most of them are though to

work with high pressure and therefore do not fulﬁll

our needs. According to the authors knowledge, the

smallest, light weight and dynamically performing

valve on the market, is currently sold by MOOG Inc.

company (Inc., 2009). The device weights only 92g,

has an hysteresis for the ﬂow characteristics < 3% ,

and a 90

phase-lag > 250Hz. Unfortunately the de-

vice is thought to work only with pressure in the range

of 160−250 ·10

Pa and it is speciﬁcally designed for

Formula-1 applications.

Therefore we started to look at the pneumatic

components, that generally are light and designed for

low pressure (up to 10 · 10

Pa). We adapted them to

work with liquids (oil), adding a precise actuation and

proper sensory features.

This document is organized as follows: next sec-

tion describes the experimental setup employed to

measure the repeatability and ﬂow-position charac-

teristic of the valve, section 3 presents the dynamic

model of the driving system, section 4 introduces a

strategy to regulate position and velocity of the valve,

section 5 presents a ﬁrst fully integrated prototype.

Finally section 6 draws the conclusions and future de-

velopments of this work.

2 EXPERIMENTAL SETUP AND

TESTING

In this section the testbed developed to evaluate the

performance of the servo valve and ﬁrst experimental

results characterising the valve are presented.

The experimental setup (ﬁgure 2) consists of the core

parts of a commercial pneumatic valve (Numatics

Inc. series Micro-Air), a stepper motor, a gear pump

providing pressure supply between 0 − 30 · 10

Pa, a

ﬂow-meter, a pressure sensor, and an electronic board

equipped with a STM32 µController.

Figure 2: CAD Model of the valve testbed.

The drive system of the valve is a 3.3 V DC step-

per motor from Nanotec working in fullstep mode,

i.e. 18 degree/step and with an holding torque of

1.6 · 10

−3

Nm. The rotor of the stepper motor is a lead

screw, driving a cylinder and thus converting the ro-

tational motor movement into a translation. The drive

is attached to the valve spool via a permanent magnet,

while the actual valve positions are determined using

an inductive sensor from Bahlluff Inc. by tracking a

steel target connected to the extended spool axis.

Control of the testbed and its components is per-

formed by a STM32 µController (series F103VE),

programmed with a special toolchain consisting of

Matlab/Simulink and Rapidstm32 Blockset, Real-

Time-Workshop and Keil Microvision µVision. The

scheme in Figure 3 sketches the general dependen-

cies of the testbed, were A and B are the connections

of the valve to the actuator chambers, P

and T are the

pressure supply line respectively the tank lines of the

gear pump, while the red lines represent the commu-

nication between the µController and the experimen-

tal setup through sensors and actors.

The two main features characterising a hydraulic

valve are:

1. repeatability of the spool movement with respect

to a certain input to the drive system.

2. ﬂow through the valve with respect to spool posi-

tion and the pressure drop over the valve.

A HIGHLY INTEGRATED LOW PRESSURE FLUID SERVO-VALVE FOR APPLICATIONS IN WEARABLE

ROBOTIC SYSTEMS

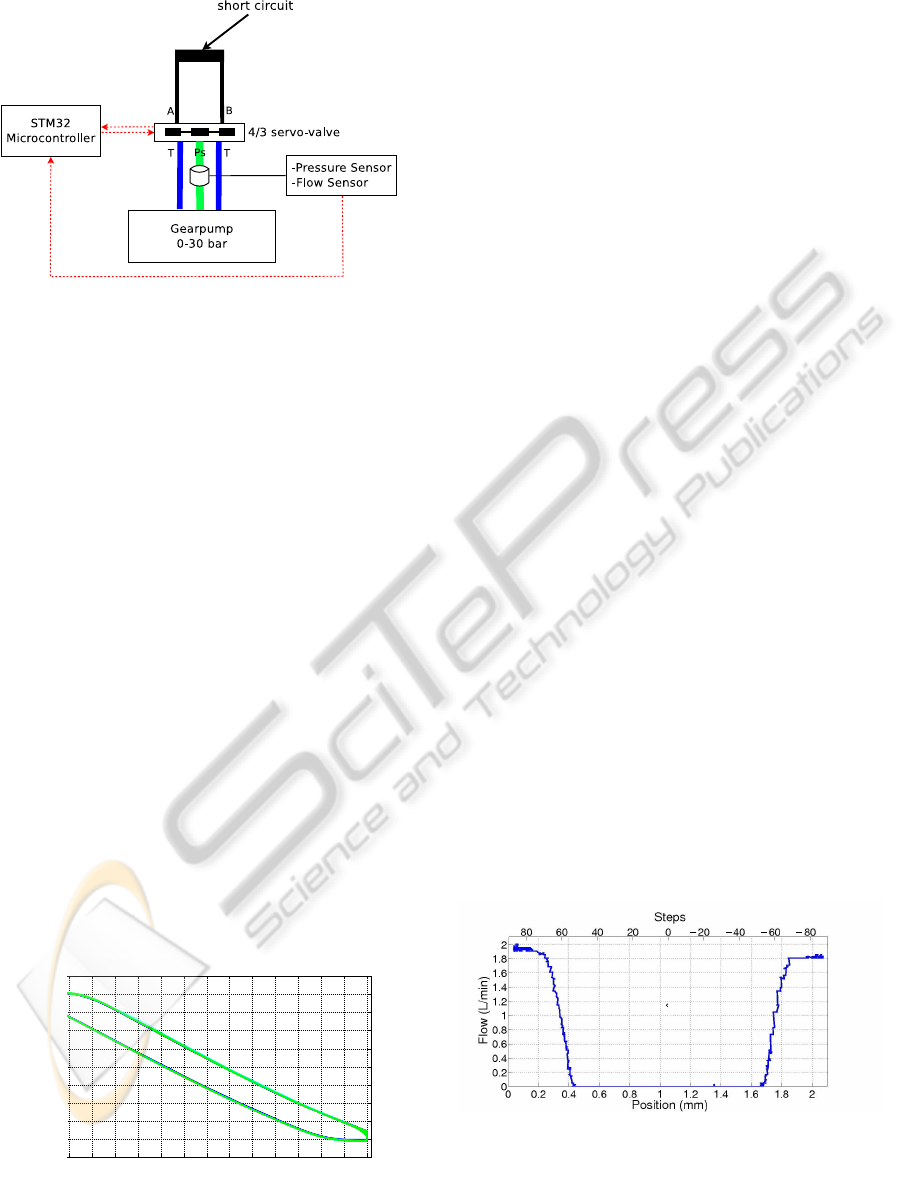
Figure 3: Scheme of experimental test setup.

Thus we focus on showing exemplary results of

these two features. Position control of the ﬂuidic

valve is presented instead in section 4.

2.1 Performance of the Drive System

In the following, the ability of the valve’s drive system

to exactly position the spool over a long time intervall

is investigated. Therefore the repeatability of valve

movement is tested, by applying a special open loop

control sequence. In the adjustment phase the spool

is driven to the center position, while in the second

phase the stepper motor is governed to move the spool

70 steps out of the zero position in both directions,

which covers almost the whole working range of the

developed prototype. Experiments took place under

inﬂuence of pressure with P

= 15 · 10

Pa. Note that

in this experiment the connectors A and B are con-

nected in short circuit, while the speed of the motor is

adjusted to its maximum of 1000 steps per second.

Figure 4 shows the open loop response of the valve

prototype to the applied control sequence. The dura-

tion of the test was 20 minutes, while data was ac-

quired for a time interval of 20 seconds every ﬁve

minutes.

−60 −50 −40 −30 −20 −10 0 10 20 30 40 50 60 70

Steps

Figure 4: Position of spool while performing 70 steps out

of center in both directions (P

= 15 · 10

Pa).

As we can obtain from Figure 4 the position re-

sponse of the drive system to the reference signal is

matching for the whole experiment. Differences for

the travel of the spool, comparing the movement out

of the center in both directions, might be caused by

friction effects. The hysteresis is due to a backlash

of approximately 10 steps (i.e. 0.1mm) between the

spindle of the stepper motor and the thread of the

cylinder moving the spool, when the motor changes

its direction of rotation. This is due to a mechani-

cal behavior and can only be reduced through higher

precision in the manufacturing process of these two

elements, or via a proper control action. Alterna-

tively a special ball-screw could be used, which pro-

vides nearly zero backlash. Overall the valve shows

remarkable repeatability for an open loop control of

spool position under inﬂuence of pressure for a long

time intervall.

2.2 Flow Characteristic of Valve

In this section the resulting static ﬂow characteristic

of the valve is presented.

To measure the ﬂow for a ﬁxed pressure drop over

the valve, the connectors A and B are again linked in

a short circuit, causing the valve to work against the

pressure in the tank line T. A ﬂowmeter from Biotech

(series VZS-007-ALU) is connected to the pressure

supply line providing a resolution of 900 pulses/L at

a maximum ﬂow of 5 L/min to the digital I/O of the

µController. Due to the fact that ﬂow needs a certain

time to become constant, the valve is driven at a very

low speed of 1 step/2s through the overall working

period. Simultaneously the average ﬂow is calculated

and sampled each second.

Fig.5 shows the static ﬂow characteristic of the hy-

draulic valve for a constant pressure drop of ∆P =

29 · 10

Pa.

Figure 5: Flow-characteristic of the valve with respect to

the spool position (∆P = 29 · 10

Pa).

From Figure 5 we can determine that the valve has

a large deadband of approximatively 1.25 mm (be-

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

tween 0.45 mm and 1.7 mm) where it is completely

closed. This is caused by the inner structure of the

valve, which is adapted from a pneumatic solenoid

valve and can neither be inﬂuenced nor changed at the

moment. Therefore this deadband has to be taken into

account in the position control structure presented in

section 4.

Having a closer look at the slopes of the ﬂow charac-

teristic, an area of about 0.2mm can be attested, where

ﬂow regulation should be possible. Driving the spool

to the extremes causes ﬂow saturation (U

≤ 0.2 mm

and 1.9mm ≤ U

), thus the overall working range of

the valve prototype can be deﬁned to

0.15mm ≤ U

≤ 1.95mm,

whereas the amplitude of the ﬂow depends on the

pressure drop over the valve.

The exemplary results shown in this section certify a

good repeatability to the drive system of the devel-

oped prototype. Furthermore the static ﬂow charac-

teristic promises a possible ﬂow regulation within the

deﬁned working range.

3 DYNAMIC MODEL

In this section a non-linear dynamic model that takes

into account the electromechanical behavior of the

stepper motor, the mechanical behavior of the spool

and the static/dynamic effects of the frictions present

within the system, was identiﬁed using a recur-

sive Hammerstein-Wiener Parameter Adaptation Al-

gorithm (PAA). The linear part of the model can be

considered as an ARX structure, well known from the

Recursive Least Squares(RLS) Algorithm described

in (I. Landau, 2006). On the other hand, the in-

put and output non-linearities with order nl of a

Hammerstein-Wiener model have the form

η(u) =

∑

k=2

(1)

η(y

lin

) =

∑

k=2

lin

(2)

with y

lin

as the output of the linear part.

Static Input

non-linearity

n(u)

Linear Dynamics

G(z)

Static Output

non-linearity

n(ylin)

u(t)

y(t)

ylin(t)

(3)

Figure 6: Block diagram of a non-linear Hammerstein-

Wiener model.

Using the equation for a Hammerstein-Wiener

models output (Guo, 2004), the structure of the PAA

becomes, with u(t) and y(t) being the real input and

output signals of the system:

θ(t +1) = θ(t) + F(t + 1)φ(t)ε

(t +1) (4)

with the Adaptation Gain

F(t + 1) = F(t) −

F(t)φ(t)φ(t)

F(t)

1 + φ(t)

F(t)φ(t)

(5)

and the Prediction Error

(t +1) = y(t + 1) −

θ(t)

φ(t). (6)

θ is the vector of computed parameters, with

θ(t)

= [ ˆa(t)

b(t)

β(t)

γ(t)

], (7)

where ˆa(t)

= [ ˆa

(t)... ˆa

(t)] are the pa-

rameters of polynomial A with order na,

b(t)

= [

(t)...

(t)] the parameters of poly-

nomial B with order nb,

β(t)

= [

(t)...

(t)] the

parameters of the input non-linearity with order nl,

γ(t)

= [

(t)...

(t)] the parameters of the output

non-linearity with order nl.

Furthermore φ(t) is the Predictor Regressor Vector

φ(t)

= [−y(t), u(t),u(t)

, ..., u(t)

, y

lin

(t)

, ..., y

lin

(t)

(8)

The output of the linear part y

lin

cannot be mea-

sured, nevertheless it can be calculated by multiplying

the parts of the predictor and the parameters vector

corresponding to the linear model:

lin

(t +1) =

θ[1 : na + nb + nl](t)φ[1 : na + nb + nl]

(9)

Finally the model output ˆy is computed

ˆy(t + 1) =

θ(t +1)

φ(t) (10)

The measured signals used for identiﬁcation are

the current absorbed by the stepper motor i

as input

signal, and position of the valvespool x

in terms of

mm as output. In order to characterize the dynamic

behavior of the valve we only considered the range

of spool positions where the ﬂow can be effectively

regulated. As a ﬁrst step the data was ﬁltered using a

bandpass ﬁlter allowing frequencies between 0Hz and

60Hz, which does not affect the dynamic range of the

model. Different models were identiﬁed starting from

distinct initial values for the parameter vector, the best

data ﬁtting reached an average of 87.49%. The out-

put of the obtained model can be seen in Figure 7,

A HIGHLY INTEGRATED LOW PRESSURE FLUID SERVO-VALVE FOR APPLICATIONS IN WEARABLE

ROBOTIC SYSTEMS

whereas the transfer function of the linear dynamic

part is given by:

G(z) =

−0.1675z − 0.1039

− 0.8512z

− 0.1351z − 0.03855

(11)

with the sample time 0.01s. The Bode diagram of

G(z) is shown in Figure 8. Finally the static input

non-linearity of the model was identiﬁed to:

η(u) = 0.59831 ∗ u

− 0.00047669 ∗ u

, (12)

while the static output non-linearity of the model is

given by:

η(y

lin

) = 0.030651 ∗ y

lin

− 0.042948 ∗ y

lin

(13)

0 200 400 600 800 1000 1200 1400 1600 1800 2000

1.5

1.55

1.6

1.65

1.7

1.75

1.8

1.85

1.9

1.95

time [cs]

Position [mm]

Real and model output

Real output

Model output

Figure 7: Comparison of the real and the model output.

Magnitude (dB)

Frequency (Rad/s)

Bode Diagram

−30

−20

−10

Figure 8: Magnitude Bode Plot of the linear transfer func-

tion.

4 VALVE CONTROL

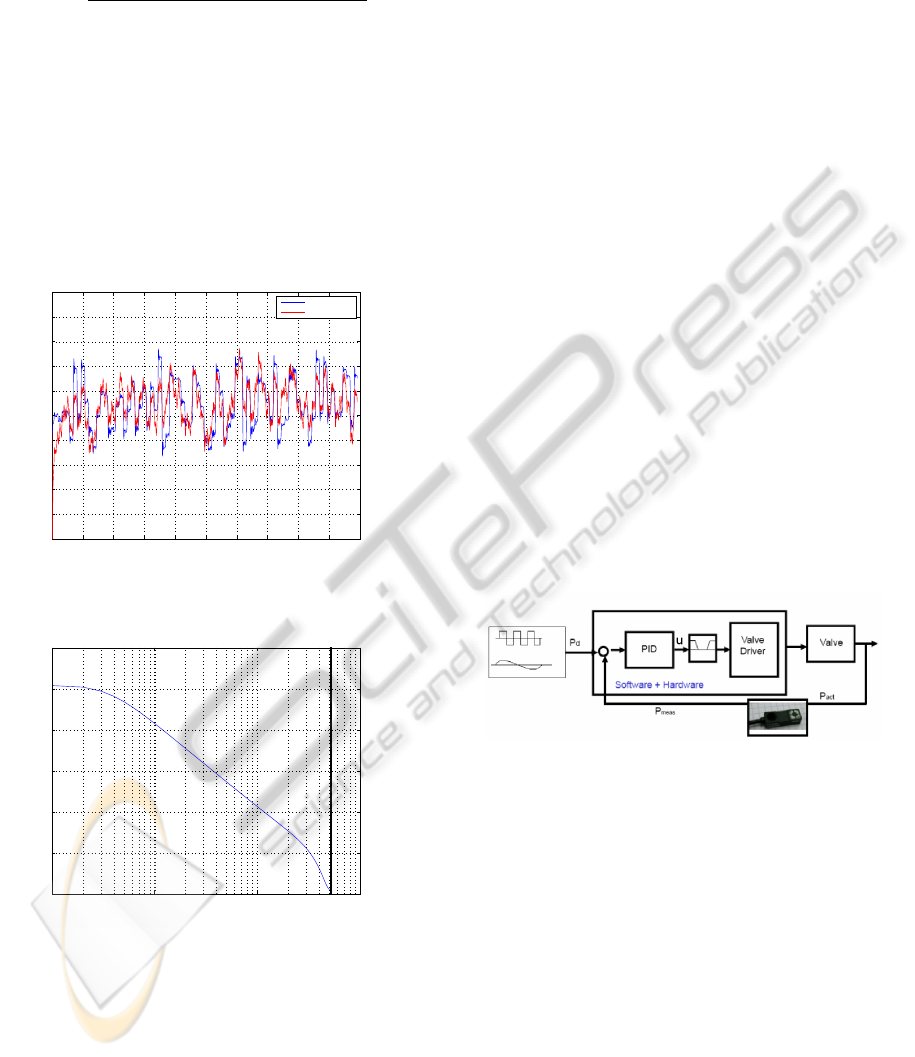
This section introduces a ﬁrst approach to control the

developed ﬂuidic valve.

Regarding the experiments shown in section 2, up to

now all movements of the spool have been performed

in open loop, i.e. no feedback of the spool position

was used. To facilitate precise position control of the

valve at a high bandwidth, the drive system is to be

controlled in closed loop, using the feedback of the

inductive sensor to track the desired trajectories given

by the µController. Therefore classical PID-control

in combination with a discretisation of stepper motor

motion is applied.

A basic requirement for position control is the ability

of the drive system to run at different speeds. Due to

the fact that the stepper motor is somehow a digital

drive, which can only have the states run or stop, a

discretising function is introduced to the control loop.

The idea is to vary the number of samples passing

between two step commands by deﬁning a variable

delay factor τ

, which causes a step command only

every τ

∗ T

, with T

as basic sampling time of the

system. Thus an increase of τ

results in a slower

motion of the valve spool, because less steps are per-

formed by the drive system in a ﬁxed time interval.

The value of τ

is set by the control action u of the

PID-controller, tracking the desired spool position p

as follows

15 − |u|·500 , u ≤ 0.03

1 , u > 0.03

(14)

Figure 9 shows the resulting scheme of the closed

loop control.

Figure 9: Scheme of discretised closed loop valve control.

Whereas p

meas

represents the measured and p

the

desired spool position. The discretising function can

be found between the PID-controller and the valve

driver.

To reject noise from the position measurement, a

moving average low-pass ﬁlter is realised via software

in the µController. The following Figure 10 shows the

modulation of the valve speed through the discretising

function.

To verify the functionality of the control startegy,

the valve is governed to execute a velocity sweep.

Starting from τ

= 100 the delay factor is decreased

by an amount of ﬁve every 5 ms until the maximum

speed at τ

= 1 is reached. After changing the

direction of movement τ

is reset to its starting value.

It is obvious that the speed of the valve is increased

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

0 2 4 6 8 10 12 14 16 18 20

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

time (s)

Position (mm)

−1.5

−1.2

−0.9

−0.6

−0.3

0.3

0.6

0.9

1.2

1.5

Velocity (mm/s)

Figure 10: Speed modulated ﬂuidic valve, blue: valve posi-

tion, green: velocity.

while the delay factor decreases and vice versa.

To test the overall performances of the developed

control scheme, sinusoidals with different frequencies

and step-like reference trajectories were supplied.

The PID’s parameters have been determined through

classical Ziegler-Nichols method, whereas the critical

controller gain and the critical oscillation period

were respectively identiﬁed as K

p,crit

= 0.58 and

crit

= 0.032 s. These results in the following con-

troller gains

= 0.35, K

= 0.02, K

= 0.004.

Figure 11 exemplary presents the tracking results of

the position control loop for step-like reference sig-

nals.

0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

time (s)

0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

(a)

(b)

Figure 11: Step-like reference tracking at (a) f=1Hz, (b)

f=3Hz, where the green line represents the reference.

As we can obtain from the ﬁgure, the controller

tracks step-like signals without overshoot up to an ac-

tual maximum frequency of f=3Hz. Due to the fact

that this test is performed in the maximum working

range, a better dynamic response can be expected for

smaller movements.

Finally Table 1 sums up the characteristic values for

a sinusoidal reference tracking, where f is the fre-

quency of the reference, e

the maximum error in

position and ϕ the phase shift between the two sig-

nals.

Table 1: Chracteristic values for sinusoidal reference track-

ing.

f in [Hz] e

in [V] ϕ in [deg]

0.5 0.028 0.81

1 0.032 1.8

3 0.11 3.24

5 THE VALVE PROTOTYPE

After the choice of the proper hardware and elec-

tronic components, a new valve was designed

and realized (ﬁgure 12) using rapid prototyping

technique. The ﬁnal device has a volume of

LxWxH=(60mm)x(20mm)x(40mm), and the version

with aluminum parts will weight approximately 80g

including one position and two pressure sensors, an

ampliﬁer board, the stepper motor, and the electri-

cal/hydraulic connectors.

Figure 12: Valve developed using rapid prototyping tec-

nique.

In this ﬁrst prototype the PWM motor driver and

the control logic are located in a separated device,

nevertheless future versions may also include these

components on-board. This will reduce the amount

of required cables to only a single power and a data

line (e.g. a CAN-BUS). Compared with other state of

the art hydraulic valves (Inc., 2009), the one here pre-

sented is designed to work with relatively low pres-

sures both for hydraulic and pneumatics purposes, it

is extremely compact and light-weight, furthermore it

integrates two pressure sensors that are directly con-

nected to the two output lines A and B (see schema in

ﬁgure 2). This allows a ﬁne tuning of the pressure in-

side the two actuator chambers, and therefore enables

a precise control of the generated torque.

A HIGHLY INTEGRATED LOW PRESSURE FLUID SERVO-VALVE FOR APPLICATIONS IN WEARABLE

ROBOTIC SYSTEMS

6 CONCLUSIONS AND FUTURE

DEVELOPMENTS

In this paper a new ﬂuid servo-valve speciﬁcally de-

signed for wearable robotic systems is presented. The

work is motivated by the fact that, according to the

authors knowledge, no commercial valve exists for

precise low pressure hydraulic actuators control. As

general requirements, compactness, light-weight, and

high dynamics were considered during the design pro-

cess. A ﬁrst series of experiments have been per-

formed to test repeatability, ﬂow-position character-

istics and dynamic response. A model of the drive

system of the servo-valve was identiﬁed using a recur-

sive Hammerstein-Wiener parameter adaptation algo-

rithm. The combination of a linear and dynamic part

with a non linear static component let to reach a ﬁt of

87%. Finally to test the overall functionality of the

valve and to measure its step response characteristics,

a proper control algorithm was implemented that al-

lows to regulate the position and the velocity of the

valve’s spool.

Further work have to be dedicated in order to iden-

tify the overall model that will explicitly deﬁne the

position-ﬂow-pressure relationship. The backlash and

deadband problems need to be properly addressed. In

particular the employment of a ball-screw for the roto-

translation mechanism of the valve, instead of a nor-

mal lead screw , will improve the precision in con-

trolling the position. Furthermore, with a customized

design of the spool, will be possible to decrease the

switching time between the two opening positions,

and therefore to improve the dynamic behavior of the

servo-valve.

ACKNOWLEDGEMENTS

The work presented in this paper was done within

the VI-Bot project, funded by the German Ministry

of Science (BMBF), [grant number 01IW07003].

REFERENCES

Folgheraiter, M., Bongardt, B., Albiez, J., and Kirchner,

F. (2008). A bio-inspired haptic interface for tele-

robotics applications. In IEEE International Con-

ference on Robotics and Biomemetics (ROBIO-2008),

Thailand, Bangkok.

Folgheraiter, M., Bongardt, B., Albiez, J., and Kirchner, F.

(2009a). Design of a bio-inspired wearable exoskele-

ton for applications in robotics. In International Joint

Conference on Biomedical Engineering Systems and

Technologies (BIOSTEC-2009), Portugal, Porto.

Folgheraiter, M., de Gea, J., Bongardt, B., Albiez, J., and

Kirchner, F. (2009b). Bio-inspired control of an arm

exoskeleton joint with active-compliant actuation sys-

tem. Applied Bionics and Biomechanics, 6(2):193–

204.

Folgheraiter, M., Schmidt, B. B. S., de Gea Fernand

ez, Al-

biez, and Kirchner, F. (2009c). Design of an arm ex-

oskeleton using an hybrid motion-capture and model-

based technique. In IEEE International Conference on

Robotics and Automation. IEEE International Confer-

ence on Robotics and Automation (ICRA-2009), May

12-17, Kobe, Japan.

Guo, F. (2004). A New Identiﬁcation Method for Wiener

and Hammerstein System. PhD thesis, Karlsruhe Uni-

versity.

Hayward, V. (1994). Experimental Robotics III, Design of

a hydraulic robot shoulder based on a combinatorial

mechanism, volume 200. Springer Berlin / Heidel-

berg.

I. Landau, G. Z. (2006). Digital Control Systems. Springer.

Inc., M. (2009). Sub miniature servovalve e024. Technical

report, http://www.moog.com/.

Jacobsen, S. C., Smith, F. M., Backman, D. K., and Iversen,

E. K. (1991). High performance, high dexterity, force

reﬂective teleoperator ii. In Proc. ANS Topical Meet-

ing on Robotics and Remote Systems.

Kahn, M. (1969). Optimal Control of a Hydraulic Arm.

PhD thesis, Stanford University M.E Dept.

Kazerooni, H., Steger, R., and Huang, L. (2006). Hybrid

control of the berkeley lower extremity exoskeleton

(bleex). The International Journal of Robotics Re-

search, 25(5-6):561–573.

Pons, J. L., editor (2008). Wereable Robots: Biomechatron-

ixs Exoskeletons. Wiley.

Raibert, M., Blankespoor, K., Nelso, G., Playter, R., and

the BigDog Team (2008). Bigdog, the rough-terrain

quaduped robot. Technical report, Waltham, MA

02451 USA.

Yoshinada, H., Yamazaki, T., Suwa, T., and Naruse, T.

(1992). Design and control of a manipulator system

driven by seawater hydraulic actuator. In Second Int.

Symposium on Measurement and Control in Robotics

(ISMCR), pages 359–364.

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics