VISUAL MAP BUILDING AND LOCALIZATION WITH AN

APPEARANCE-BASED APPROACH

Comparisons of Techniques to Extract Information of Panoramic Images

Francisco Amor

os, Luis Pay

Oscar Reinoso, Lorenzo Fern

andez and Jose M

Mar

ın

Departamento de Ingenier

ıa de Sistemas Industriales

Miguel Hern

andez University, Avda. de la Universidad s/n. 03202, Elche (Alicante), Spain

Keywords:

Robot mapping, Appearance-based methods, Omnidirectional vision, Spatial localization.

Abstract:

Appearance-based techniques have proved to constitute a robust approach to build a topological map of an

environment using just visual information. In this paper, we describe a complete methodology to build

appearance-based maps from a set of omnidirectional images captured by a robot along an environment.

To extract the most relevant information from the images, we use and compare the performance of several

compressing methods. In this analysis we include their invariance against rotations of the robot on the ground

plane and small changes in the environment. The main objective consists in building a map that the robot

can use in any application where it needs to know its position and orientation within the environment, with

minimum memory requirements and computational cost but with a reasonable accuracy. This way, we present

both a method to build the map and a method to test its performance in future applications.

1 INTRODUCTION

The applications that require the navigation of a robot

through an environment need the use of an internal

representation of it. Thanks to it, the robot can esti-

mate its position and orientation regarding the map it

has with the information captured by the sensors the

robot is equipped with. Omnidirectional visual sys-

tems can be stood out due to the richness of the in-

formation they provide and their relatively low cost.

Classical researches into mobile robots provided with

vision systems have focused on the extraction of natu-

ral or artiﬁcial landmarks from the image to build the

map and carry out the localization of the robot (Thrun,

2003). Nevertheless, it is not necessary to extract such

kind of landmarks to recognize where the robot is. In-

stead of this, we can process the image as a whole.

These appearance-based approaches are an interesting

option when dealing with unstructured environments

where it may be hard to ﬁnd patterns to recognize the

scene. With these approaches, the comparisons are

made using the whole information of the scenes. As a

disadvantage, we have to work with a huge amount of

information, thus having a high computational cost,

so we need to study compression techniques.

There are several researches that show compres-

sion techniques that can be used. For example, PCA

(Principal Components Analysis) is a widely used

method that has demonstrated being robust applied

to image processing, (Krose et al., 2007). Due to

the fact that conventional PCA is not a rotational in-

variant method, other authors introduced a PCA ap-

proach that, although being computationally heavier,

takes into account the images with diverse orienta-

tions (Jogan and Leonardis, 2000). There are authors

that use the Fourier Transform as a generic method to

extract the most relevant information of an image. In

this ﬁeld, (Menegatti et al., 2004) deﬁnes the Fourier

Signature, which is based on the 1D Discrete Fourier

Transform of the image rows and gets more robust-

ness dealing with different orientation images. On the

other hand, (Dalal and Triggs, 2005) used a method

based on the Histogram of Oriented Gradients (HOG)

to the pedestrian detection, proving that it could be a

useful descriptor for computer vision and image pro-

cessing using the objects’ appearance.

(Paya et al., 2009) present a comparative study of

appearance-based techniques. We extend this study,

taking into account three different methods: Fourier

Signature, PCA over Fourier Signature and HOG.

423

Amorós F., Payá L., Reinoso Ó., Fernández L. and Marín J. (2010).

VISUAL MAP BUILDING AND LOCALIZATION WITH AN APPEARANCE-BASED APPROACH - Comparisons of Techniques to Extract Information of

Panoramic Images.

In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 423-426

DOI: 10.5220/0002949404230426

 SciTePress

2 REVIEW OF COMPRESSION

TECHNIQUES

In this section we summarize some techniques to ex-

tract the most relevant information from a database

made up of panoramic images trying to keep the

amount of memory to a minimum.

2.1 Fourier-based Techniques

As shown in (Paya et al., 2009) it is possible to rep-

resent an image using the Discrete Fourier Transform

of each row. Taking proﬁt of the Fourier Transform

properties, we just keep the ﬁrst coefﬁcients to rep-

resent each row since the most relevant information

concentrates in the low frequency components of the

sequence. Moreover, as we are working with omnidi-

rectional images, when the Fourier Transform of each

row is computed, another very interesting property

appears: rotational invariance. Due to the fact that

the rotation of a panoramic image is represented as

a shift of its columns, the Fourier Transform compo-

nent’s module will be the same. So, the amplitude of

the transforms is the same as the original, and just the

phase changes. Therefore, we can ﬁnd out the rela-

tive rotation of two images by comparing its Fourier

coefﬁcient phases.

2.2 PCA over Fourier Signature

PCA-based techniques have proved to be a very use-

ful compressing methods. They make possible that,

having a set of N images with M pixels each, ~x

∈

ℜ

Mx1

, j = 1.. . N, we could transform each image in

a feature vector (also named projection of the image)

∈ ℜ

kx1

, j = 1 . . .N, being K the PCA features con-

taining the most relevant information of the image,

k ≤ N. However, if we apply PCA directly over the

matrix that contains the images, we obtain a database

with information just with the orientation of the robot

when capturing those images but not for other possi-

ble orientations. What we propose in this point is to

transform the Fourier Signature components instead

of the image, obtaining the compression of rotational

invariant information, joining the advantages of PCA

and Fourier techniques.

2.3 Histogram of Oriented Gradient

The Histogram of Oriented Gradient descriptors

(HOG) (Dalal and Triggs, 2005) are based on the ori-

entation of the gradient in local areas of an image. Ba-

sically it consist in computing the orientation binning

of the image by dividing it in cells, and creating the

histogram of each cell, obtaining module and orienta-

tion of each pixel. The histogram is computed based

on the gradient orientation of the pixels within the

cell, weighted with the corresponding module value.

An omnidirectional image contains the same pixels in

a row although the image is rotated, but in a different

order. So, if we calculate the histogram of cells with

the same width as the image, we obtain an array of

rotational invariant characteristics.

However, to know the relative orientation between

two rotated images vertical windows are used, with

the same height of the window, being able to vary

its width and application distance. Ordering the his-

tograms of these windows in a different way, we ob-

tain the same results as calculating the histogram of

a rotated image with an angle proportional to the dis-

tance between windows. That also will determine the

accuracy in orientation computation.

3 LOCALIZATION AND

ORIENTATION RECOVERING

In this section, we measure the goodness of each algo-

rithm by assessing the results of calculating the pose

of the robot with a new image compared to a map

created previously. All the functions and simulations

have been made using Matlab R2008b under Max OS

X. The maps have been made up of images belonging

to a database got from Technique Faculty of Biele-

feld University (Moeller et al., 2007). They were col-

lected in three living spaces under realistic illumina-

tion conditions. All of them are structured in a 10x10

cm rectangular grid. The images were captured with

an omnidirectional camera, and later converted into

panoramic ones with 41x256 pixel size. The number

of images that compose the database varies depend-

ing on the experiment, since, in order to assess the ro-

bustness of the algorithms, the distance between the

images of the grid we take will be expanded. In the

results shown in this paper, the grid used is 20x20cm,

with 204 images.

The test images used to carry out the experiments

is made up of all the available images in the database,

with 15 artiﬁcial rotations of each one (every 22.5

◦

11,936 images altogether . Because the pose includes

the position and orientation of the robot, both are

studied separately. Position is studied with recall and

precision measurement (Gil et al., 2009). Each chart

shows the information about if a correct location is

in the Nearest Neighbour (N.N.), i. e., if it is the

ﬁrst result selected, or between Second or Third Near-

est Neighbours (S.N.N or T.N.N). Regarding the rota-

tion, we represent the results accuracy in bar graphs

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

424

depending on how much they differ from the correct

ones. If the experiment error is bigger than ±10 de-

grees, it is considered as a fail and not taken into ac-

count.

3.1 Fourier Signature Technique

The map obtained with Fourier Signature is repre-

sented with two matrices: the module and the phase of

the Fourier Coefﬁcients. With the module matrix we

can estimate the position of the robot by calculating

the Euclidean distance of the power spectrum of that

image with the spectra of the map stored, whereas the

phase vector associated to the most similar image re-

trieved is used to compute the orientation of the robot

regarding the map created previously.

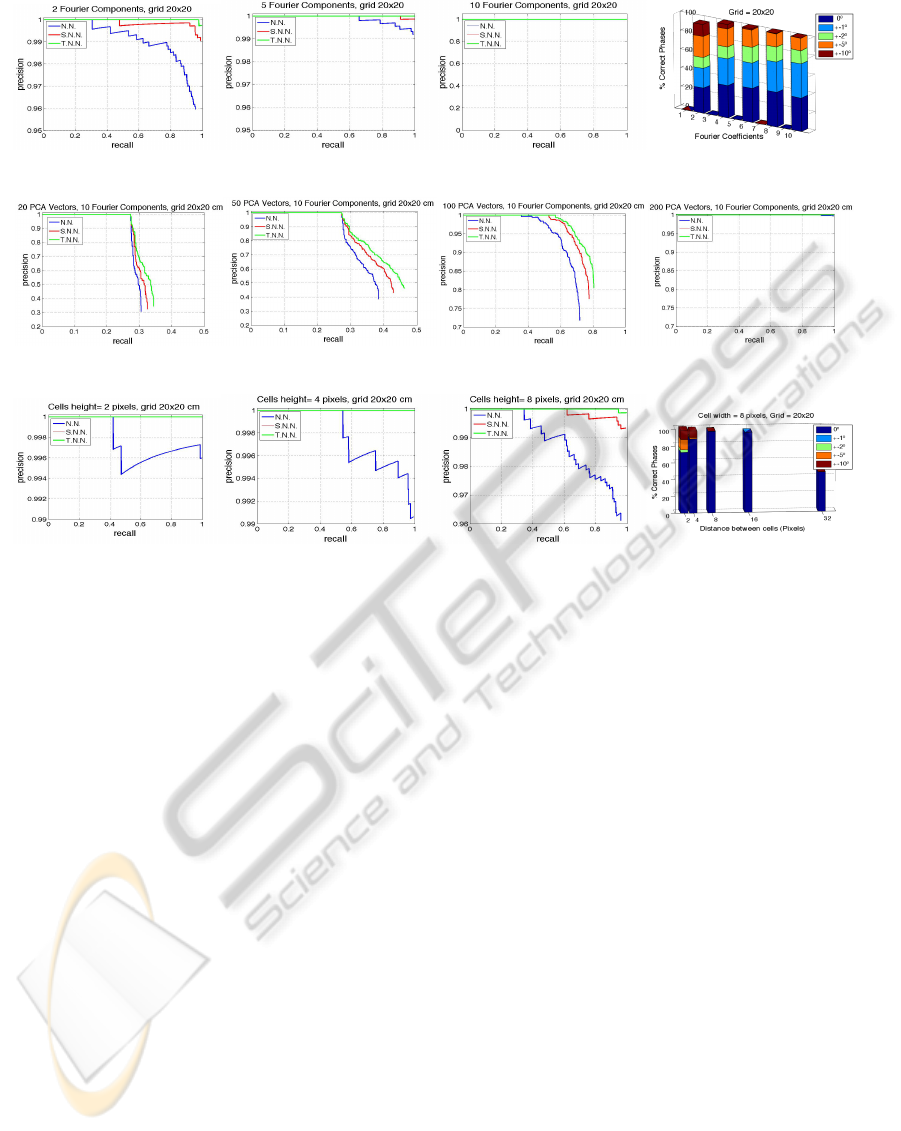
Figure 1 (a),(b),(c) show recall and precision mea-

sures. We can see that when we take more coefﬁ-

cients, the location is better, but there is a limit where

it is not interesting to raise the number of elements we

take because the results do not improve. The phase

accuracy (Figure 1(d)) also improves when more co-

efﬁcients are used to compute the angle, although is

quite constant when we take 8 or more components.

It can be stressed that with just 2 components (Figure

1(a)) we have 96 percent accuracy when we study the

Nearest Neighbour, and almost 100 percent when we

keep the three Nearest Neighbours.

3.2 PCA over Fourier Signature

After applying PCA over Fourier Signature mod-

ule matrix, we obtain another matrix containing the

main eigenvectors selected, and the projection of the

map images onto the space made up with that vec-

tors. These are used to calculate the position of the

robot. On the other hand, we keep the phase matrix

of Fourier Signature directly to estimate the orienta-

tion. To know where the robot is, ﬁrst the Fourier

Signature of the current position image must be com-

puted. After selecting the corresponding coefﬁcients

of each row, we project the vector of modules onto the

eigenspace, and ﬁnd the most similar image through

Euclidean distance. When the position is known, the

phase is calculated the same way than when we do not

apply PCA since the phase matrix is not modiﬁed.

As we can see in Figure 1(e),(f),(g),(h), if we are

looking for a high accuracy in the localization task,

it is required a high number of PCA eigenvectors,

what means loosing the advantages of applying this

method. Moreover, in the majority of the experi-

ments, the number of Fourier coefﬁcients we need is

bigger than when we do not use PCA, incrementing

the memory used. Phase results are not included be-

cause the results are exactly the same as showed in

Figure 1(d) since its calculation method does not vary.

3.3 Histogram of Oriented Gradient

When a new image arrives, we need to calculate its

histogram of oriented gradient using cells with the

same size of those we used to build the map. So, the

time needed to ﬁnd the pose of the robot varies de-

pending on both vertical and horizontal cells we use.

To ﬁnd the location of the robot the horizontal cell in-

formation is used, whereas to compute the phase we

need the vertical cells. In both cases, the informa-

tion is found by calculating the Euclidean distance be-

tween the histogram of the new image and the stored

ones in the map. The recall-precision charts (Figure

1(i),(j),(k)) shows that the more windows to divide the

image, the better accuracy we obtain. However, it is

not a notably difference between the cases. Regard-

ing the orientation (ﬁg 1(l)), although the results are

good, it can be stressed that, when the window appli-

cation distance is greater than 2 pixels, the results are

like binary variables, appearing just cases with zero

gap, or failures, which is to say that the error is zero

or greater than 10 degrees.

4 CONCLUSIONS

This work has focused on the comparison of different

appearance-based algorithms applied to the creation

of a dense map of a real environment, using omni-

directional images. We have presented three differ-

ent methods to compress the information in the map.

All of them have demonstrated to be valid to carry

out the estimation of the pose of a robot inside the

map. Fourier Signature has proved to be the most ef-

ﬁcient method since taking few components per row

we obtain good results. No advantages have been

found in applying PCA to the Fourier signature, since

in order to have good results it is needed to keep the

great majority of the eigenvectors obtained and more

Fourier coefﬁcients. In both cases the orientation ac-

curacy depends just on the number of Fourier com-

ponents, and the error in its estimation is less than

or equal to 5 degrees is the great majority of sim-

ulations. Regarding HOG, results demonstrate it is

a robust method in localization task, having slightly

worse results than Fourier algorithm ones. However

the orientations computing is less effective due to fact

that the degrees are sampled depending the number

of windows we use, determining that way its accu-

racy. This paper shows again the wide range of possi-

bilities of appearance-based methods applied to mo-

VISUAL MAP BUILDING AND LOCALIZATION WITH AN APPEARANCE-BASED APPROACH - Comparisons of

Techniques to Extract Information of Panoramic Images

425

(a) (b) (c) (d)

(e) (f) (g) (h)

(i) (j) (k) (l)

Figure 1: (a), (b), (c) Recall-Precision charts with N.N., S.N.N. and T.N.N and (d) phase accuracy using Fourier Signature

varying number of components. (e), (f), (g), (h) Recall-Precision charts with N.N., S.N.N. and T.N.N using PCA over Fourier

Signature varying number of PCA vectors. (i), (j), (k) Recall-Precision charts with N.N., S.N.N. and T.N.N and (l) phase

accuracy using HOG varying horizontal window’s height.

bile robotics, and its promising results encourage us

to continue studying them in deep, looking for new

available techniques or improving the robustness to

illumination changes for them.

ACKNOWLEDGEMENTS

This work has been supported by the Spanish govern-

ment through the project DPI2007-61197.

REFERENCES

Dalal, N. and Triggs, B. (2005). Histograms of oriented

gradients fot human detection. In Proc of the IEEE

Conf on Computer Vision and Pattern Recognition,

San Diego, USA. Vol. II, pp. 886-893.

Gil, A., Martinez, O., Ballesta, M., and Reinoso, O. (2009).

A comparative evaluation of interest point detectors

and local descriptors for visual slam. Machine Vision

and Applications (MVA).

Jogan, M. and Leonardis, A. (2000). Robust localization

using eigenspace of spinning-images. In Proc. IEEE

Workshop on Omnidirectional Vision, Hilton Head Is-

land, USA, pp. 37-44. IEEE.

Krose, B., Bunschoten, R., Hagen, S., Terwijn, B., and

Vlassis, N. (2007). Visual homing in enviroments with

anisotropic landmark distrubution. In Autonomous

Robots, 23(3), 2007, pp. 231-245.

Menegatti, E., Maeda, T., and Ishiguro, H. (2004). Image-

based memory for robot navigation using properties of

omnidirectional images. In Robotics and Autonomous

Systems. Vol. 47, No. 4, pp. 251-276.

Moeller, R., Vardy, A., Kreft, S., and Ruwisch, S. (2007).

Visual homing in enviroments with anisotropic land-

mark distrubution. In Autonomous Robots, 23(3),

2007, pp. 231-245.

Paya, L., Fernandez, L., Reinoso, O., Gil, A., and Ubeda,

D. (2009). Appearance-based dense maps creation.

In 6th Int Conf on Informatics in Control, Automation

and Robotics ICINCO 2009. Ed. INTICC PRESS - pp.

250-255.

Thrun, S. (2003). Robotic mapping: A survey, in exploring

artiﬁcial intelligence. In The New Milenium, pp. 1-35.

Morgan Kaufmann Publishers, San Francisco, USA.

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

426