REAL-TIME CONTROL OF REWINDING MACHINE

Comparison of Two Approaches

Karel Perutka

Faculty of Applied Informatics, Tomas Bata University in Zlin, nam. T.G.M. 5555, Zlin, Czech Republic

Keywords: Nonlinear control, MATLAB, Off-line identification, On-line identification, Real-time control, Self-tuning

control.

Abstract: The paper deals with two simple approaches applied to the real-time control of rewinding machine and their

comparison. In brief, the comparison of results obtained by nonlinear real-time control with pre-

identification, and by adaptive real-time control with on-line identification was performed. The rewinding

machine was controlled by PC from MATLAB’s Real-Time Toolbox using technological card, terminal

board and wires. Each of two used approaches has its advantages and its drawbacks, which was proven, and

nonlinear control seemed to be more suitable for the rewinding machine, minimally because of the action

signal history from the nonlinear control, the action is more consistent.

1 INTRODUCTION

As is stated in abstract, the comparison of two

approaches of rewinding machine’s real-time control

was performed. Firstly, let us provide introduction to

the control methods which were used.

Many processes can be marked as multivariable

systems. For such processes, the centralized

controller is commonly used because it provides the

best closed loop performance. However, the

centralized controller is less fault tolerant than the

decentralized controller. This is the main reason why

decentralized control strategy is often preferred. The

used strategy is based on the linear model of the

nonlinear plant and the design of a decentralized

controller for this linear model (Li, et al., 2000). Li,

et al., (2000) mentions that the plant decomposition

is crucial for decentralized design and it is not

always possible to obtain satisfactory decentralized

control systems using a simple physical

decomposition. However, the decentralized

approach has one big disadvantage due to the

decomposition, the reduction of control performance

due to the restricted controller structure (Cui and

Jacobsen, 2002). But decentralized control is

popular in practice, see (Balachandran and

Chidambaram, 1997).

Many nonlinear systems can be identified and

controlled as linear systems around the steady state

or working points. Nice application of feedback

control was performed by Cottenceau et al.

(Cottenceau et al., 2001). When nonlinear control is

used, it possible to enlarge the working interval even

in the case the linear control does not guarantee the

sufficient quality of control. Moreover, some

systems have nonlinearities, which cannot be

linearly approximated, for instance friction, etc.

Therefore, the necessity of nonlinear control occurs.

Nonlinear system is a set of elements of system,

in which at least one of the elements is nonlinear

(Modrlak, 2008).

Some nonlinear systems can be approximated by

linear systems within the defined range and when

specific conditions hold on. In practice, such

systems can be divided into linear and nonlinear

part. The dynamics of system can be approximated

by linear model and its nonlinear part by the

nonlinear characteristics. The superposition is not

valid for the nonlinear systems, the output of

Hammerstein model is different from the output of

Weiner model (Lin, 1994).

This paper uses the simple nonlinear control

introduced by Chen et al. (Chen et al., 2006) for

nonlinear real-time control of rewinding machine.

The simple nonlinear control was applied for

instance by Perutka and Dostalek (2009), the

application is in MATLAB because it is nice tool for

Control Engineering at universities (Perutka,

Hezcko, 2007).

197

Perutka K. (2010).

REAL-TIME CONTROL OF REWINDING MACHINE - Comparison of Two Approaches.

In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 197-200

DOI: 10.5220/0002949501970200

 SciTePress

2 THEORETICAL

BACKGROUND

2.1 Simple Nonlinear Controller

This method was introduced by Chen et al. (Chen, et

al., 2006) and verified by Perutka and Dostalek

(Perutka and Dostalek, 2009). The controller

consists of three parts, “the pure controller” and

generator giving together the nonlinear controller

and the system model inversion (Chen, et al., 2006).

2.2 Pre-identification

Suppose the existence of continuous-time

multivariable N x N system S(t). Moreover, let as

assume the vector of reference signals R(t), its

values are send to the input of the system S(t). They

are same and for the same time as those one which

are going to be used during the control. Each time

interval of history of control of the system S(t),

where all reference signals have the constant value,

is identified separately. Every identification element

is identified several times, every time with different

identification algorithm, and the obtained model is

verified with the measured data. The obtained model

which gives the best agreement with the measured

data is used for control.

2.3 Self-tuning Control

Self-tuning controllers (STC) belong to the class of

adaptive control systems. Self-tuning controllers are

based on on-line identification and on tuning the

controller parameters with respect to identified

changes in controlled systems (Bobal et al., 2005).

2.4 On-line Identification

The action (input) signal u(t) is continuously

approximated by Lagrange regression polynomial at

the interval of given length during entire control.

After the polynomial approximation, the

approximating polynomial derivation u

(i)

(t) is

counted. It is sampled in purpose to count the values

of subsystem parameters using recursive

identification algorithm.

2.4.1 Recursive Least-squares and Recursive

Instrumental Variable

Least squares method is generally known, for

instance presented by Bobal et al. (Bobal et al.,

2005). Instrumental variable method is a

modification of the least squares method. It does not

allow us to obtain the properties of noise, but it has

inferior presumptions than the least square method

(Zhu & Backx, 1993).

2.5 Suboptimal Linear Quadratic

Tracking Controller

Usage of adequate method of controller parameters

computation is crucial for control. Linear quadratic

control is a reliable method verified by many

publications, for instance by Casavola et al.

(Casavola et al., 1991), the used suboptimal method

was introduced by Dostal (Dostal, 1997).

3 SHORT DESCRIPTION OF

USED APPROACHES

The overall controlled system was controlled in the

view of decentralized control. Nice paper useful to

decentralized control was written by Seatzu and Usai

(Seatzu and Usai, 2002).

3.1 Approach 1

This approach is a combination of simple nonlinear

control (chap. 2.1) and pre-identification (chap. 2.2).

Firstly, the pre-identification run and it provided the

initial parameters estimates for the model used

during nonlinear control.

3.2 Approach 2

Approach 2 is de facto self-tuning control in real-

time. The controller parameters were counted

according to the suboptimal linear quadratic method

(chap. 2.5), identification was realized using least

squares and instrumental variable (chap. 2.2.1).

4 MACHINE DESCRIPTION

The real-time control was realized on CE108

Coupled Drives Apparatus, see figure 1, which is

manufactured by TecQuipment Ltd., United

Kingdom. The rewinding machine is adapted for its

usage in the laboratory. The properties of the

apparatus had been studied in detail and its model in

MATLAB – SIMULINK environment was created

(Perutka, Dolezel 2009). The speed and tension of

thread during spooling is an example of rewinding

process. This situation is modified for laboratory

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

198

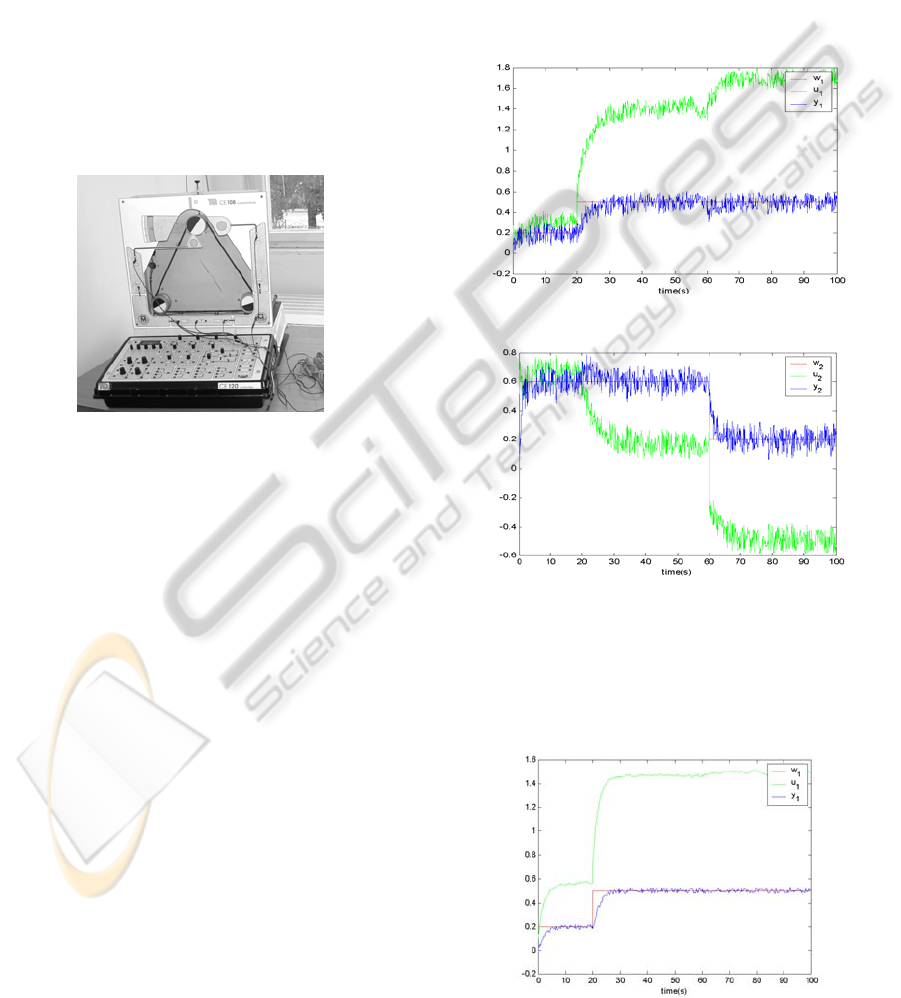
experiments where the flexible belt is fastened on

three wheels. Speed of two wheels is directly

proportional to the number of revolutions of the

servo-motors. Third wheel may move, because it is

fixed on the moving jib which is hung on the spring.

The measurement of speed and tension is indirect

via the angle of the moving jib, from -10 deg to 10

deg, which correspond the voltage from -10 V to 10

V. The control voltages of the amplifiers of the

servo-motors, which are bi-directional, are the

inputs. The outputs are four, the voltage of the speed

of two servo-motors, or two wheels respectively, and

the voltage of the tension and the speed of the belt,

or angular deflection and speed of 3rd wheel

respectively. The apparatus is connected to PC via

technological card Advantech. The control is

realized in MATLAB using Real Time Toolbox.

Figure 1: CE108 Rewinding Machine.

5 REAL-TIME TOOLBOX

DESCRIPTION

Real Time Toolbox is used for real-time control and

it is based on a high performance real-time kernel

and drivers for popular A/D and D/A boards, the

toolbox includes drivers for more than 300 industry-

standard data acquisition boars. The real-time kernel

allows us to use sampling frequencies up to 66 kHz

with no external clock source required. Besides

standard analog and digital I/O many specialized

devices are also supported. Multiple boards of the

same or different type can be used simultaneously to

offer sufficient I/O even for complex industrial

applications (Real-time Toolbox: Introduction,

2010).

6 EXPERIMENTAL PART

In figures 2-5 there are obtained results of real-time

control of rewinding machine. In these figures, the

meaning of the symbols is following: w

– set-point

of first subsystem, u

– action signal of first

subsystem, y

– output signal of first subsystem, w

– set-point of second subsystem, u

– action signal

of second subsystem, y

– output signal of second

subsystem.

Figures 2 and 3 provide the results obtained by

adaptive real-time control. It was the self-tuning

control with online identification using least squares

(figure 2) and instrumental variable method (figure

3). The suboptimal linear quadratic tracking was

used as the method of controller parameters tuning.

Figure 2: Adaptive real-time control – 1

subsystem.

Figure 3: Adaptive real-time control – 2

subsystem.

Figures 4 and 5 provide the results obtained by

nonlinear real-time control, the combination of

simple nonlinear controller (Chen et al., 2006) with

pre-identification. The pre-identification provided

the initial estimates of the used model’s parameters.



Figure 4: Nonlinear real-time control – 1

subsystem.

REAL-TIME CONTROL OF REWINDING MACHINE - Comparison of Two Approaches

199

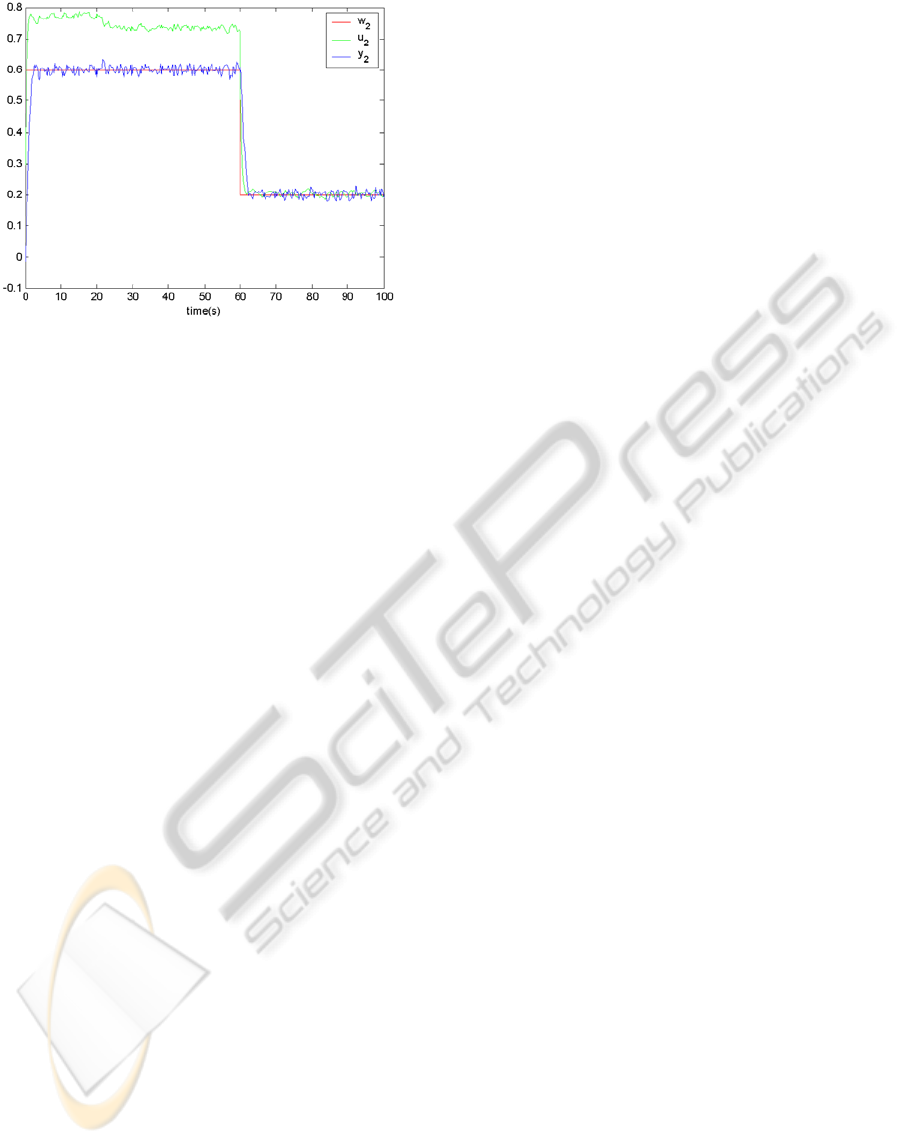
Figure 5: Nonlinear real-time control – 2

subsystem.

Both used methods of real-time control provided

the satisfactory results and they can be used for this

machine, but there are some differences which

should be mentioned. Nonlinear real-time control is

less biased and seemed to be more suitable. The

usage of pre-identification decreased the unwanted

overshooting caused by interactions. Moreover, the

adaptive real-time control is notably more sensitive

to the changes of model parameters, whilst the used

nonlinear real-time control does not need the change

of model parameters.

7 CONCLUSIONS

The paper presented results of real-time control of

rewinding machine by two approaches together with

the necessary theoretical background. The nonlinear

real-time control seems to be more suitable, but

adaptive real-time control is also possible to use,

because it is more sensitive on the changes during

control.

ACKNOWLEDGEMENTS

The author would like to mention MSM7088352102

grant, from which the work was supported.

REFERENCES

Balachandran, R., Chidambaram, M., 1997. Decentralized

control of crude unit distillation towers. In Computers

and Chemical Engineering, 21, pp. 783-786.

Bobal, V., Böhm, J., Fessl, J., Machacek, J., 2005. Digital

Self-tuning Controllers. Springer-Verlag London

Limited.

Casavola, A., Grimble, M. J., Mosca, E., Nistri, P., 1991.

Continuous-time LQ regulator design by polynomial

equations. In Automatica, 27, pp. 555-558.

Chen, Ch.-T.; Chuang, Y.-Ch., Hwang, Ch., 2006. A

Simple Nonlinear Control Strategy for Chemical

Processes. In Proc. of the 6th Asian Control

Conference, Inna Grand Bali Beach Hotel, Bali,

Indonesia, ISBN 979-15017-0.

Cottenceau, B., Hardouin, L., Boimond, J.-L., Ferrier, J.-

L., 2001. Model reference control for time event

graphs in diods. In Automatica, 37, pp. 1451-1458.

Cui, H., Jacobsen, E.W., 2002. Performance limitations in

decentralized control. In Journal of Process Control,

12, pp. 485-494.

Dostal, P., 1997. An approach to control of processes of

chemical technology. Inaugural dissertation. TU Brno,

Brno.

Li, H., Lee, P. L., Bahri, P., Cameron, I.T., 2000.

Decentralized control design for nonlinear plants: ν–

metric approach. In Computers and Chemical

Engineering, 24, pp. 273-278.

Lin, C.-F., 1994. Advanced Control System Design. New

Jersey, USA: Prentice Hall, 1994. ISBN 0-13-006305-

Modrlak, O.: Theory of automatic control II: Nonlinear

systems. Lectures notes. [on line] Technical University

of Liberec, [cit. 02-02-2010], available at

http://www.fm.vslib.cz/~krtsub/fm/modrlak/pdf/tar2_n

el.pdf.

Perutka, K., Dolezel, K., 2009. Simulation Model of

CE108 Coupled Drives Apparatus. In MATHMOD

2009, 6th Vienna Conference on Mathematical

Modelling, Vienna, Austria. ARGESIM.

Perutka, K., Dostalek, P., 2009. Simple Decentralized

Autonomous Adaptive Nonlinear Real-time Controller

with Controller Source Code Optimization: Case

Study. In ISADS 2009, 9th IEEE International

Symposium on Autonomous Decentralized Systems,

Athens, Greece. IEEE.

Perutka, K., Heczko, K., 2007. Teaching of MATLAB

Programming Using Complex Game. In FIE2007,

37th IEEE/ASEE Frontiers in Education Conference,

Milwaukee, WI, USA. IEEE.

Real-time Toolbox: Introduction. [on line] Humusoft, [cit.

03-30-2010], available at http://www.humusoft.cz/

produkty/rtt/.

Seatzu, C., Usai, G., 2002. A decentralized volume

variations observer for open channels. In Applied

Mathematical Modelling, 26, pp. 975-1001.

Zhu, Y., Backx, T., 1993. Identification of Multivariable

Industrial Processes for Simulation, Diagnosis and

Control

. Springer-Verlag Ltd., London, United

Kingdom

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

200