PASSIVITY-BASED APPROACH TO DEPLOYMENT IN

MULTI-AGENT NETWORKS

Heath LeBlanc, Emeka Eyisi, Nicholas Kottenstette, Xenofon Koutsoukos and Janos Sztipanovits

Institute for Software Integrated Systems (ISIS), Vanderbilt University, 2015 Terrace Place, Nashville, TN 37203, U.S.A.

Keywords:

Passivity, Compositionality, Deployment, Overlay network, Input-output stability, Distributed protocol.

Abstract:

Surveillance and convoy tracking applications often require groups of networked agents for redundancy and

better coverage. An important goal upon deployment is to establish a formation around a target. Although there

exist distributed algorithms using only local communication that achieve this goal, they typically ignore desta-

bilizing effects resulting from implementation uncertainties, such as network delays and data loss. This paper

resolves these issues by introducing a discrete-time distributed design framework that uses a compositional,

passivity-based approach to ensure l

-stability regardless of overlay network topology, in the presence of net-

work delays and data loss. For the restricted case of a uniform node degree in the overlay network topology,

the paper shows that asymptotic formation establishment is achieved. Finally, simulations of velocity-limited

unmanned air vehicles (UAVs) are presented that demonstrate the robustness of the network architecture to

network delays and data loss.

1 INTRODUCTION

Modern surveillance and convoy tracking applica-

tions often require deploying groups of unmanned

aerial vehicles (UAVs). The beneﬁt of using multi-

ple UAVs is redundancy, which reduces the likelihood

of missing interesting events on the ground, in the

presence of obstructions caused by nonuniform ter-

rain, vegetation, or man-made structures. Further, the

additional UAVs provide greater breadth of coverage.

A central task for such multi-agent systems is to es-

tablish a formation around an area of interest. For

example, an n-gon with a target as its center, at the

appropriate radius, may simultaneously provide sig-

niﬁcant redundancy and breadth of coverage.

Performing coordinated tasks in multi-

agent systems using only local information has

been studied extensively over the past decade

(Olfati-Saber et al., 2007), (Ren et al., 2005),

(Olfati-Saber, 2006). Typically, in group coordi-

nation the desired formation emerges from the design

of the control law. In (Fax and Murray, 2004), the

so-called information ﬁlter is used for formation sta-

bility of LTI systems. For coordination of nonlinear

systems, contraction theory with wave variable com-

munication (Wang and Slotine, 2006), explicit design

of Lyapunov vector ﬁelds (Lawrence et al., 2008),

and passivity (Arcak, 2007), (Ihle et al., 2007),

(Bai et al., 2008), (Igarashi et al., 2008), have been

used successfully.

Much of the above work - especially the passivity-

based methods - has considered continuous-time

systems; however, for implementation discrete-

time design is needed. In addition, implementa-

tion uncertainties such as network delays and data

loss must be taken into consideration. This pa-

per focuses on decoupling the control design and

discrete-time implementation by using a passivity-

based framework inspired by work in telemanip-

ulation (Chopra et al., 2008), port-Hamiltonian sys-

tems (Stramigioli et al., 2005), and network control

(Kottenstette et al., 2009).

The unifying concept in the aforementioned work

is the scattering formalism, which has traditionally

been applied to power variables (effort and ﬂow)

while closing the loop on velocity. In this work, the

scattering formalism is used abstractly (without the

physical interpretation) to close the loop on position.

The contributions of this paper are three-fold.

First, we introduce a compositional network control

system (NCS) design approach that guarantees pas-

sivity of the networked system. Secondly, we show

that the coupled multi-agent network is l

-stable for

any bidirectional overlay network with asymmetric

LeBlanc H., Eyisi E., Kottenstette N., Koutsoukos X. and Sztipanovits J. (2010).

A PASSIVITY-BASED APPROACH TO DEPLOYMENT IN MULTI-AGENT NETWORKS.

In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 53-62

DOI: 10.5220/0002951500530062

 SciTePress

delays whenever the input-output mapping of each

agent is strictly-output passive. The stability re-

sult holds for packet-switched networks using easily

enforced constraints. Thirdly, for the single-input,

single-output (SISO) case, we perform steady-state

analysis and we show that the multi-agent network

can establish an n-gon upon deployment. Finally, we

provide simulations using Simulink/TrueTime to il-

lustrate the approach for controlling velocity-limited

quadrotor UAVs. Simulink is a graphical user envi-

ronment (GUI) used for the modeling, simulation, and

analysis of dynamical systems (MathWorks, 2008).

TrueTime extends Simulink with platform related

modeling concepts (i.e., networks, clocks, sched-

ulers) and supports simulation of networked and em-

bedded control systems with implementation effects

(Ohlin et al., 2007).

The rest of the paper is organized as follows: Sec-

tion 2 provides the formal problem statement and

other preliminaries. The distributed NCS design

framework is introduced in Section 3. The main the-

oretical results are detailed in Section 4. Section 5

presents simulations in Simulink/TrueTime illustrat-

ing our results. Finally, Section 6 provides concluding

remarks and future work.

2 PRELIMINARIES

Consider the problem of n agents establishing a for-

mation around a target in R

. Assume a global inertial

coordinate system and suppose the starting positions

of the agents are arbitrary. The goal is to establish

an n-gon, where the n agents tend to the coordinates

of the vertices asymptotically. Formally, we assign a

vertex ν

of the n-gon to agent i, with position x

(k),

i = 1,2,. .. ,n. Then we require

lim

k→∞

(k) −ν

= 0. (1)

We consider a network of n interacting agents with

communication topology described by a connected

undirected graph, G = (V,E), where V = {1,2,...,n}

describes the agents and E ⊂V ×V models the bidi-

rectional communication. Additionally, each bidirec-

tional link may have asymmetric, time-varying de-

lays. The delays are denoted d

i j

(k) for link (i, j) ∈ E.

For the purpose of analysis, it is useful to intro-

duce the adjacency matrix, A = [a

i j

], associated with

graph G (Godsil and Royle, 2001). For an undirected

graph, the adjacency matrix is a symmetric matrix

(i.e., A = A

), and is mathematically deﬁned by

i j

(

1 (i, j) ∈E;

0 (i, j) /∈ E.

(2)

Additionally, we deﬁne the set of neighbors, N

, of a

node i as those nodes which send messages to i, given

by N

= {j ∈V |a

6= 0}. Finally, we denote the num-

ber of neighbors by |N

| = n

The agents communicate and process signals in

the extended

-space of functions that map

∪{

}

to R

, denoted l

, which are mapped onto l

by the

truncation operator deﬁned by

( f )

(

f (k) 0 ≤ k ≤ N −1;

0 otherwise.

(3)

Further, for all f , g ∈ l

deﬁne

hf , gi

N−1

∑

k=0

(k)g(k). (4)

We use deﬁnitions for l

-stability and passiv-

ity for discrete-time systems, which are anal-

ogous to the continuous-time counterparts in

(van der Schaft, 1999):

Deﬁnition 1. Given a discrete-time system deﬁned by

its input-output mapping, G : l

→ l

, the discrete-

time system is l

-stable if

u ∈ l

=⇒ G(u) ∈ l

. (5)

Deﬁnition 2. Let G: l

→ l

. Then, for all u ∈l

1. G is passive if there exists some constant β ∈ R

(called the bias) such that

hG(u),ui

≥ −β, ∀N ∈ N; (6)

2. G is strictly output passive if there exists some

constants β ∈ R and ε > 0 such that

hG(u),ui

≥ εk(G(u))

−β, ∀N ∈ N. (7)

We assume a synchronous network, with period

T .

Further, each agent shares information only lo-

cally (no global shared resources). However, the de-

sired setpoints are calculated prior to deployment. Fi-

nally, the agents begin execution at time index k = 0.

3 NCS DESIGN

This section details the distributed network control

system (NCS) design. The objective is to provide

a passive-by-construction, discrete-time multi-agent

network. In general, the overlay network is bidi-

rectional with asymmetric delays. For simplicity,

consider the three node network shown in Figure 1.

We assume the agents use a clock synchronization

algorithm prior to deployment to ensure this assumption

holds.

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

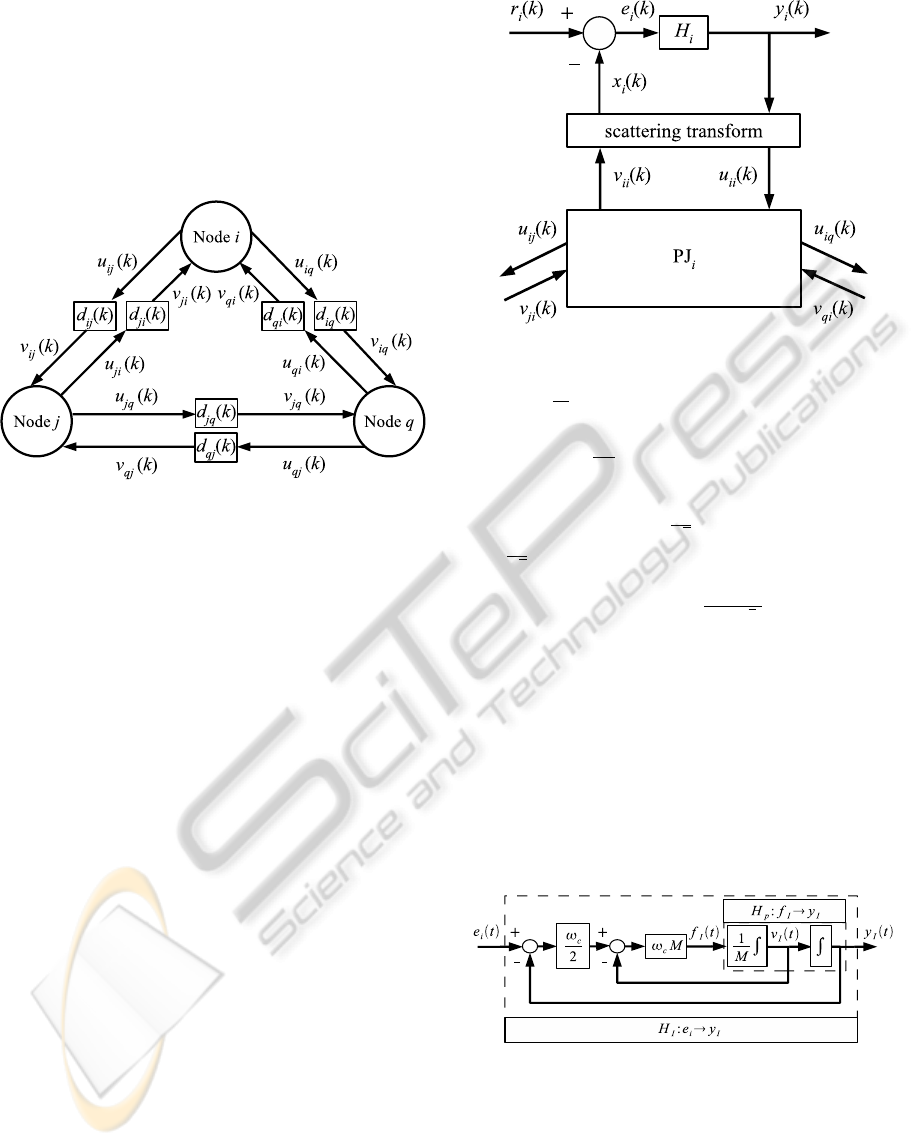
Each node represents a UAV, with each edge model-

ing the communication between UAVs. Realistically,

each link in the network is subject to delay imposed

by packet handling and transmission delays. This

is modeled by the time-varying delays (e.g., d

i j

(k)),

shown in Figure 1. The u and v variables in the ﬁg-

ure are power wave variables, which are described in

Section 3.2.

Figure 1: A three node network with time-varying delays in

the communication links.

3.1 Agent Model

The agent model is shown in Figure 2. Each agent i

receives an input reference, r

, which inﬂuences the

output, y

, of the agent through the system mapping,

. H

describes a compensated plant, and is re-

quired to be strictly output passive. The variables x

and y

are transformed into the wave domain through

the scattering transformation. The node’s wave vari-

ables u

and v

are coupled to other nodes through

a power junction, PJ

, which allows two or more sys-

tems to be connected in a passivity-preserving manner

(Kottenstette et al., 2009). The scattering transforma-

tion and power junction are crucial to ensuring pas-

sivity of the networked system and will be described

in the next section.

For simplicity, we model the UAVs with a point

mass along two dimensions. We denote the point

mass system, H

: f

→ y

, in which f

∈ R

is the

inertial control force and y

∈ R

is the inertial posi-

tion as depicted in Figure 3. The equations of motion

are

˙y

(t) = v

(t)

M ˙v

(t) = f

(t).

Using the point mass model for each agent i, we

design an inertial position control system, which we

denote H

: e

→y

, shown in Figure 3. The inner loop

gain of the compensator is ω

M (ω

> 0) and the outer

Figure 2: Node architecture.

loop gain

. The overall equation of motion

¨y

= −ω

˙y

−

−e

) = −2ζω

˙y

−ω

−e

)

clearly indicates a stable second order system with

natural frequency ω

√

and damping coefﬁcient

ζ =

√

, where y

= e

at steady state. It can be shown

that the inertial position control system is inside the

sector [a,1], where a = −

2(1+

√

(Zames, 1966),

(Kottenstette and Porter, 2009). Therefore, the sys-

tem H

: e

→ y

is not strictly output passive; how-

ever, by adding a high-pass ﬁlter in parallel, the sys-

tem may be rendered strictly output passive, as de-

picted in Figure 4 (with c = 2). Since e

= y

at steady state, the inertial position of the sys-

tem may be directly controlled. This model is dis-

cretized using a bilinear-like transform, called the

inner-product equivalent sample and hold (IPESH)

transform, which preserves the conic properties of the

system (Kottenstette et al., 2009).

Figure 3: Inertial position control system.

3.2 Network Model

In distributed control applications the information

transmitted across the network has inherent physical

meaning. It is well known that transforming these

physical variables into the wave domain can preserve

A PASSIVITY-BASED APPROACH TO DEPLOYMENT IN MULTI-AGENT NETWORKS

Figure 4: Strictly output passive inertial position control

system.

passivity and stability for a single bidirectional con-

nection (Chopra et al., 2008) and for star networks

(Kottenstette et al., 2009). In this paper, we extend

these approaches to distributed networks with arbi-

trary overlay topology. The network model is dis-

tributed in the sense that all nodes in the network com-

municate only locally.

We formally deﬁne the scattering transformation

as follows. For each i ∈V , the scattering transforma-

tion produces power waves u

(k) and v

(k) deﬁned

(k) =

√

(k) + x

(k)), (9a)

(k) =

√

(k) −x

(k)). (9b)

This deﬁnition is similar to the one in

(Niemeyer and Slotine, 2004), with the force and

velocity variables replaced with x

and y

. In general,

we place no restriction on the physical meaning of x

and y

; however, for our UAV model, x

and y

denote

position. The scattering transformation is treated

as a mathematical deﬁnition, with the characteristic

impedance, b

, having appropriate units for physical

consistency.

Next, we deﬁne the power junction, which allows

two or more systems to be connected in the wave do-

main in a passivity-preserving manner.

Deﬁnition 3. Fix m, p ∈ N, p ≥ 2. Then, a power

junction is a function f : l

→ l

, which satisﬁes

for all ξ ∈ l

and all k ∈Z

the inequality

(k)ξ(k) ≥ f (ξ(k))

f (ξ(k)). (10)

The vector ξ(k) in the deﬁnition of the power junc-

tion is formed by concatenating the p inputs in l

into

a single mp-dimensional column vector. For analyz-

ing our network model, it is useful to pair the p in-

puts to their corresponding outputs in the output col-

umn vector, f (ξ(k)), and partition the set of pairs into

two disjoint sets S

and S

out

. These sets denote the

net ﬂow of power into and out of the power junction,

respectively. Formally, for i ∈ S

and o ∈ S

out

, let

∈ l

denote the inputs and v

∈ l

denote

the outputs of the power junction. Then (10) may be

rewritten as

∑

i∈S

(k)u

(k) −v

(k)v

(k) ≥

∑

o∈S

out

(k)u

(k) −v

(k)v

(k).

(11)

We implement each node’s power junction as a

linear set of equations. Speciﬁcally, we use the fol-

lowing equations. For each i ∈V, j ∈N

, and k ∈ Z

the outgoing waves are computed as

i j

(k) =

√

(k), (12a)

(k) =

√

∑

j∈N

(k). (12b)

Although the functional form of the power junc-

tion is not constrained to be linear, these equations

simplify the steady state analysis and exhibit a local

averaging behavior in regular networks. This can be

seen as follows. Consider the wave variables that in-

ﬂuence the power junction at a given node i, shown

in Figure 5, and suppose n

= n

≡ η, ∀i, j ∈V (i.e.,

a regular network). Then, for each j ∈ N

, v

(k) =

(k −d

(k)). Thus, an expression for v

(k) is given

(k) =

√

∑

j∈N

(k)

√

∑

j∈N

(k −d

(k))

√

∑

j∈N

√

j j

(k −d

(k))

∑

j∈N

j j

(k −d

(k)).

Therefore, in regular networks, the input wave vari-

able, v

(k), is the average of its neighbors’ delayed

output wave variables, u

j j

(k −d

(k)), j ∈ N

Due to the presence of delays and data loss

some (or all) of the v

(k) may not be received at

time k, in which case v

(k) , 0. Handling de-

layed and dropped packets as null packets satisﬁes

the synchronous assumption and preserves passivity

(Chopra et al., 2008). Before proceeding to describe

the constraints on delayed and lost data, we prove our

claim that the implementation given by (12) satisﬁes

the deﬁnition of a power junction.

Lemma 1. The implementation deﬁned by (12) satis-

ﬁes the power junction constraint.

Proof: From the remarks following the power

junction deﬁnition, it is sufﬁcient to show that (12)

satisfy (11). Clearly, a sufﬁcient condition for satis-

fying (11) is to enforce the following constraints for

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

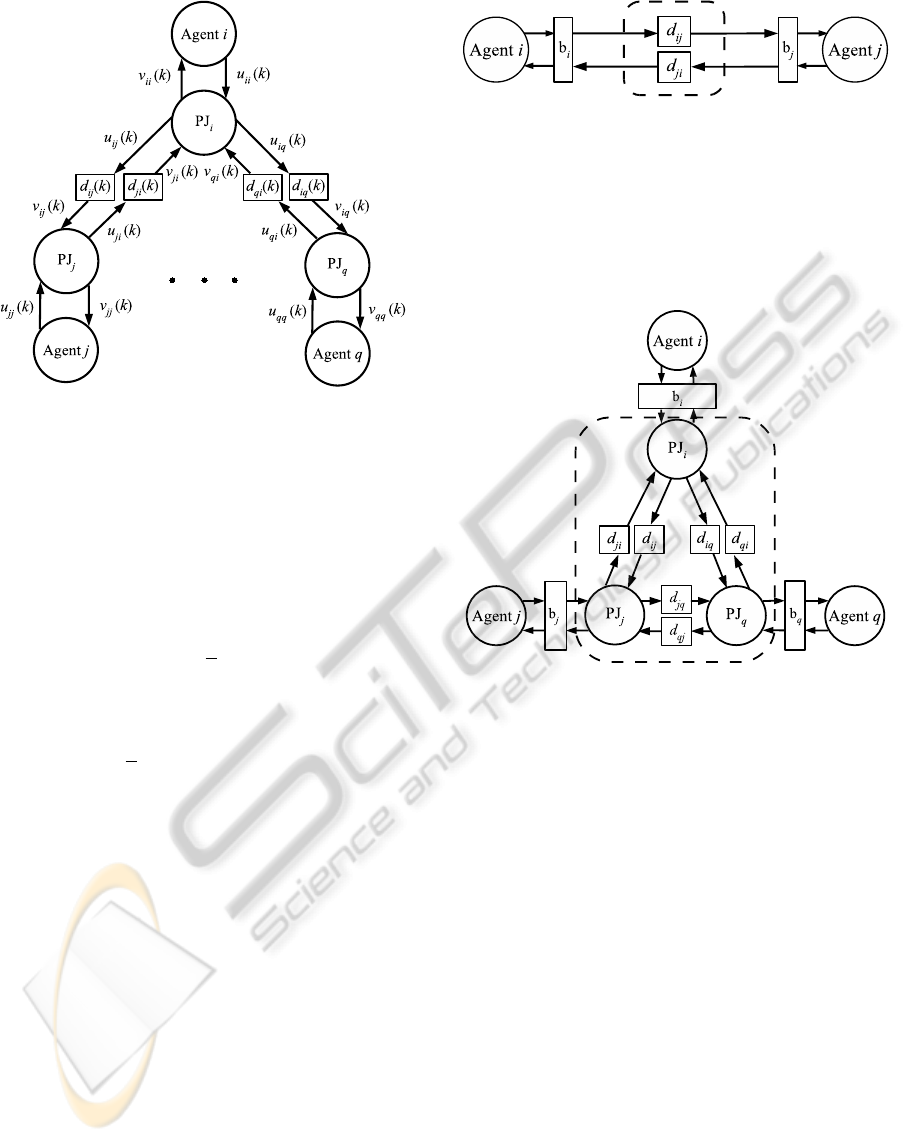
Figure 5: The neighbors of a node, showing the wave vari-

ables inﬂuencing the node through the power junction.

each component l = 1,2,...,m,

∑

j∈N

i j

(k) ≤u

(k), (13a)

(k) ≤

∑

j∈N

(k), (13b)

where S

= {ii} and S

out

= {i j | j ∈N

}. To show that

(13a) is satisﬁed, we use (12a), which yields

∑

j∈N

i j

(k) =

∑

j∈N

(k) = u

(k).

For (13b) we combine (12b) with the Cauchy-

Schwartz inequality to get

(k) =

(

∑

j∈N

(k))

≤

∑

j∈N

(k).

Finally, we constrain the network model by pre-

venting retransmission of data for each agent. Also,

as mentioned above, whenever receiver’s buffers are

empty, we process null packets. Based on these as-

sumptions, each channel (i, j) ∈ E satisﬁes the fol-

lowing inequality regardless of time-varying delays

and data loss (Chopra et al., 2008),

k(v

i j

)

≤ k(u

i j

)

, holds ∀N ∈N. (14)

This inequality states that each channel, viewed as the

input-output mapping shown in Figure 6, is passive.

4 ANALYSIS

4.1 Passivity of the Networked System

In this section we ﬁrst prove that the network model

is passive and then show that the input-output map-

Figure 6: A point-to-point connection using the scattering

formalism to ensure passivity of the bidirectional connec-

tion subject to asymmetric time-varying delays, shown in-

side the dashed box.

ping describing the networked system is strictly out-

put passive. Figure 7 shows the passive network. The

following lemma proves that the portion inside the

dashed box of Figure 7 is passive.

Figure 7: A three node network illustrating the passive net-

work, shown inside the dashed box.

Lemma 2. Consider a network of n interacting dy-

namic systems constrained to the design framework

described in Section 3. Then, the global energy con-

straint

∑

i=1

{k(u

)

−k(v

)

} ≥ 0 (15)

is satisﬁed for all N ∈ N, regardless of time-varying

delays and data loss.

Proof: Sum the power constraints (11) of each

node i, with S

= {ii} and S

out

= {i j | j ∈ N

}, from

time k = 0 to k = N −1 and sum the resulting inequal-

ities over all nodes (rearranging the terms in the sums

appropriately). Then, invoke (14) to obtain

∑

i=1

{k(u

)

−k(v

)

}

≥

∑

i=1

∑

j∈N

i j

{k(u

i j

)

−k(v

i j

)

}

≥ 0.

A PASSIVITY-BASED APPROACH TO DEPLOYMENT IN MULTI-AGENT NETWORKS

The energy constraint of (15) also implies that

collectively, the mapping from the x

to the y

, i =

1,. .. ,n, is passive (see Figure 2). To show this, con-

sider the following power constraint, which may eas-

ily be derived from (9a) and (9b)

(k)u

(k) −v

(k)v

(k)) = y

(k)x

(k). (16)

Substitute (16) into (15) to obtain

∑

i=1

≥ 0. (17)

Deﬁne x(k) and y(k) as the nm ×1 column vectors

formed by concatenating the x

(k) and y

(k), respec-

tively, of each node. Then, it follows that

hy,xi

≥ 0,

which satisﬁes the deﬁnition of passivity (6), with β =

We conclude the section by proving that the entire

networked system (e.g., the three node system in Fig-

ure 7) is strictly output passive for arbitrary network

topologies.

Theorem 1. Consider a network of n interacting dy-

namic systems constrained to the design framework

described in Section 3. Deﬁne r(k) and y(k) as the

nm ×1 column vectors formed by concatenating the

(k) and y

(k), respectively, of each node. Finally,

deﬁne the input-output mapping H : l

→ l

such

that H(r(k)) = y(k). Then, H is strictly output pas-

sive.

Proof: Since each H

is strictly output passive,

there exists ε

> 0 and β

, for all i ∈V , such that

≥ ε

k(y

)

−β

. (18)

Making the substitution, x

(k) = r

(k)−e

(k) into (17)

and using the linearity of the inner-product, gives

∑

i=1

≥

∑

i=1

. (19)

Substituting (18) into (19) yields

∑

i=1

≥ ε

∑

i=1

k(y

)

−β, (20)

where ε = min

{ε

} and β =

∑

i=1

. Finally, we

rewrite (20) as

hy,ri

≥ εk(y)

−β. (21)

4.2 Stability

The previous result shows that the networked system

deﬁned by the mapping H is strictly output passive. It

then follows that H is l

-stable.

Theorem 2. The mapping H(r(k)) = y(k) deﬁned in

Theorem 1 is l

-stable.

Proof: We begin with the notion of ﬁnite l

-gain.

The map G has ﬁnite l

-gain if there exists ﬁnite con-

stants γ,β such that for all N ∈ N

k(G(u))

≤ γk(u)

+ β, ∀u ∈l

. (22)

It is well known in continuous-time

(van der Schaft, 1999) and has been shown for

discrete-time (Kottenstette and Antsaklis, 2007) that

a sufﬁcient condition for a system to have ﬁnite

-gain is for the system to be strictly output passive.

Therefore, by Theorem 1, H has ﬁnite l

-gain.

Now suppose u ∈ l

(i.e., kuk

< ∞). Then take

N →∞ in (22). This leads to

kG(u)k

≤ γkuk

+ β < ∞, ∀u ∈ l

Therefore, H(u) ∈l

. By Deﬁnition 1, H is l

-stable.

From the proof of Theorem 2, we see that any

system that is strictly output passive is necessarily

-stable. Therefore, each agent described by H

inherently stable. The beneﬁt of the passivity-based

network framework is that it ensures that interactions

caused by the network do not destabilize the net-

worked multi-agent system. This result holds even in

the presence of time-varying delays and data loss (un-

der the assumptions outlined in Section 3.2) because

the passivity results hold. Moreover, the networked

multi-agent system will remain stable regardless of

network topology.

4.3 Steady-state Analysis

To analyze the behavior of the coupled multi-agent

system, we consider the system at steady-state. In

order to do this, we assume that each strictly output

system, H

, admits a steady-state solution whenever a

constant input is applied. With this assumption, there

exists a steady-state solution for the multi-agent sys-

tem (provided there is no data loss), since the rest of

the networked system is linear. For simplicity, we as-

sume the system is SISO. If the degrees of freedom of

the system are decoupled, this result may be applied

to MIMO systems.

Theorem 3. Consider a network of n interacting

SISO agents designed using the framework described

in Section 3 and ignore time delays and data loss. As-

sume the inputs, r

, reach steady-state and consider

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

the outputs, y

, as k → ∞. If H

at each node i has

steady-state gain g

, then the steady-state output of

node i is given by

√

∑

j∈N

√

[

−1

+ r

]

(23)

Proof: Since time delays and data loss are ig-

nored, we drop the time index. Using the relation

= r

−x

and replacing H

with g

, the input-output

relation y

= H

) may be written as

= g

−x

). (24)

Next, substituting (24) into (9b) and solving for x

yields

−

√

. (25)

Substituting (25) into (24) and reducing gives us

√

. (26)

Combining v

= u

with (12a) at node j (roles of j

and i are reversed), produces

√

j j

Substituting this into (12b) for node i yields

√

∑

j∈N

√

j j

. (27)

Now, solving (24) at node j for x

and substituting

into (9a) at node j produces

j j

√

−1

+ r

(28)

Substitute (28) into (27) to get

√

∑

j∈N

√

−1

+ r

(29)

Finally, substitute (29) into (26) to obtain (23). 2

Theorem 3 provides a system of n equations de-

scribing the system asymptotically (as k → ∞). The

system of equations described by (23) are clearly cou-

pled and depend on the overlay network structure. For

the case of a regular topology, the following corol-

lary characterizes the system of equations and pro-

vides the means to precalculate the reference inputs

to asymptotically achieve a desired setpoint. For the

two-dimensional agent model described in Section

3.1 the two degrees of freedom are decoupled, so we

use this corollary to establish an n-gon around the tar-

get, as described in Section 2.

Corollary 1. Consider a network of n SISO agents

with a regular overlay network topology (i.e., n

≡ η ∀i, j ∈ V ). If all of the systems H

have iden-

tical steady-state gain g and each scattering trans-

formation has the same impedance b, the system of

steady-state equations may be written as

y =

bg+1

r +

bg−1

y + r]

, (30)

where y and r are deﬁned in Theorem 1 and A is

the adjacency matrix of the regular overlay network

topology. Assuming the inverse of (ηI + A) exists, we

may solve this equation for r to obtain

r =

(ηI + A)

−1

((bg + 1)ηI −(bg −1)A) y. (31)

5 SIMULATIONS

The experimental setup involves a network of eight

UAVs that communicate in a regular overlay network

topology, each with degree η = 4, and a synchronous

sampling period of T = 0.01 seconds. Each UAV

moves in the plane, inﬂuenced by its own input and

the wave variables received from its neighbors. We

model the UAVs as described in Section 3.1, so that

each has a steady state gain, g = 1, and characteris-

tic impedance, b = 1. The dynamics of the velocity

limited UAVs are implemented using Simulink mod-

els while TrueTime is used to simulate the network

dynamics and communication between neighboring

UAVs. The network protocol used is IEEE 802.11b,

with a speed of 11 Mbps.

5.1 Evaluation

We present ﬁve scenarios to demonstrate our design

framework.

Experiment 1: Nominal Case. In this experiment,

delays and data loss are ignored. Figure 8a shows a

plot of the eight UAVs enclosing the target at the ori-

gin, within a radius of 100m. The data points show

the evolution of the UAVs from their initial positions

to their ﬁnal positions. The UAVs cooperatively en-

close the target and each agent is 100m away from the

target, thus achieving the desired goal.

Figure 8b shows the x-positions of four agents

(UAVs 1, 3, 5, and 8) over a period of 200 seconds.

The desired x-positions for the four agents are 100m,

0m, 0m and -100m, respectively. These values corre-

spond to the desired conﬁguration and are achieved in

about 160 seconds.

Figure 9 shows the average and maximum errors

of all the UAVs’ positions relative to the desired con-

ﬁguration. From the ﬁgure, the average and maxi-

mum error reach the value of zero after 160 seconds

A PASSIVITY-BASED APPROACH TO DEPLOYMENT IN MULTI-AGENT NETWORKS

−500 0 500

−500

−400

−300

−200

−100

100

200

300

400

500

x−position(m)

y−position(m)

UAVs and Target Locations

at 0s

Target

at 1s

at 20s

at 200s

(a) UAVs and target positions.

0 50 100 150 200

−500

−400

−300

−200

−100

100

200

300

400

500

Time(S)

x−position(m)

Plot of UAVs’ x−positions

UAV1

UAV3

UAV5

UAV8

(b) Plot of UAVs’ x-position over time.

Figure 8: Network of UAVs (nominal case).

0 50 100 150 200

100

200

300

400

500

600

700

800

Time(s)

Error(m)

Average and Maximum Errors of UAV positions

Average Error

Maximum Error

Figure 9: Average and maximum errors of UAVs’ positions

(nominal case).

which corresponds to the time the UAVs achieve the

desired conﬁguration.

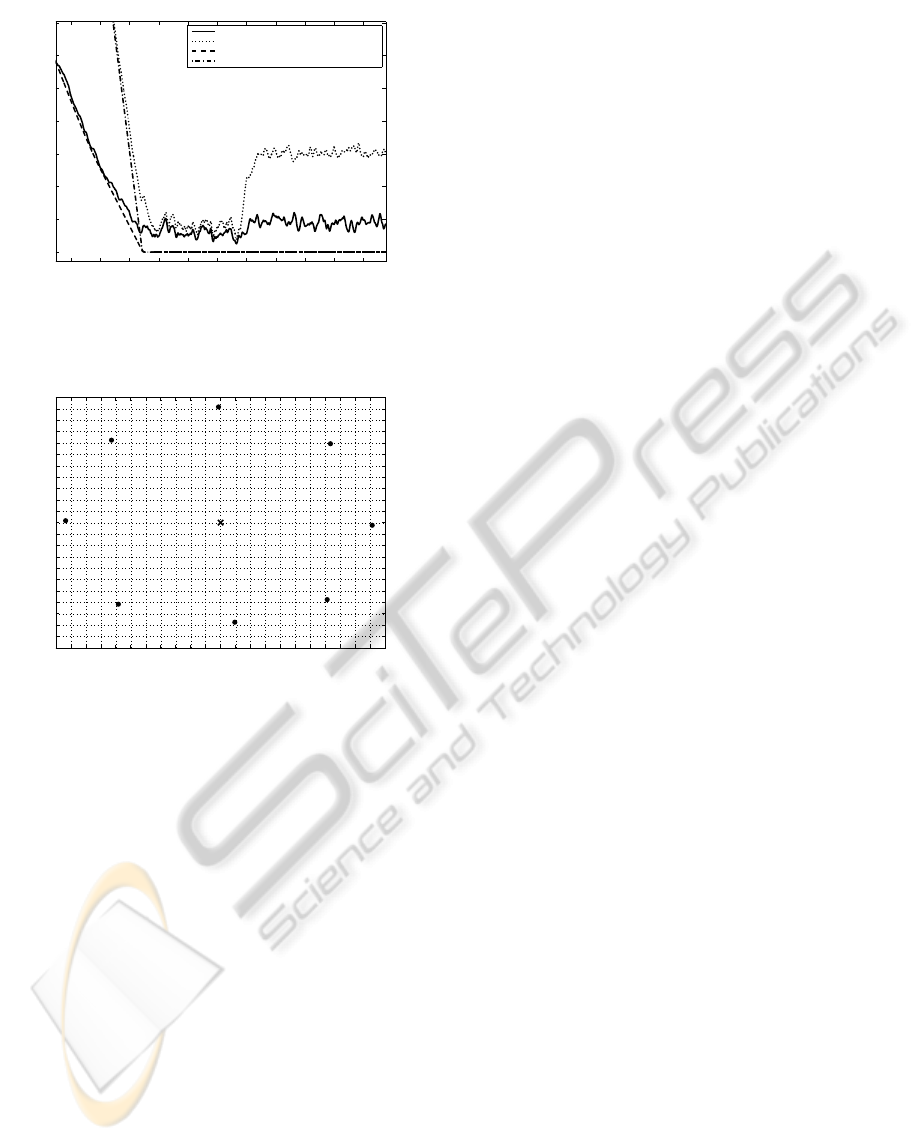
Experiment 2: Nonuniform Constant Time De-

lays. This experiment demonstrates the robustness of

155 160 165 170 175 180 185 190 195 200 205

0.05

0.1

0.15

0.2

Time(s)

Error(m)

Average and Maximum Errors of UAV Positions

Average Error(Delay Case)

Maximum Error(Delay Case)

Average Error(Nominal Case)

Maximum Error(Nominal Case)

Figure 10: Average and maximum errors of UAVs’ po-

sitions (nonuniform constant delay in all communication

channels).

150 160 170 180 190 200

Time(s)

Error(m)

Average and Maximum Errors of UAV positions

Average Error(Packet Loss Case)

Maximum Error(Packet Loss Case)

Average Error(Nominal Case)

Maximum Error(Nominal Case)

Figure 11: Average and maximum errors of UAVs’ posi-

tions (ten percent probability of packet loss).

155 160 165 170 175 180 185 190 195 200

0.02

0.04

0.06

0.08

0.1

0.12

0.14

0.16

0.18

0.2

Time(s)

Error(s)

Average and Maximum Errors of UAV Positions

Average Error(Time−Varying Delay Case)

Maximum Error(Time−Varying Delay Case)

Average Error(Nominal Case)

Maximum Error(Nominal Case)

Figure 12: Average and maximum errors of UAVs’ posi-

tions (time-varying delay case).

the distributed network of UAVs to nonuniform con-

stant delays. We introduce nonuniform time delays,

between 1 to 10 seconds, in all the communication

channels of the network. Figure 10 shows the average

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

130 140 150 160 170 180 190 200 210 220 230

Time(s)

Error(m)

Average and Maximum Errors of UAV Positions

Average Error( Combined Network Effects)

Maximum Error( Combined Network Effects)

Average Error(Nominal Case)

Maximum Error(Nominal Case)

Figure 13: Average and maximum errors of UAVs’ posi-

tions (time-varying delay and packet loss case).

−110−100−90 −80 −70 −60 −50 −40 −30 −20 −10 0 10 20 30 40 50 60 70 80 90 100 110

−110

−100

−90

−80

−70

−60

−50

−40

−30

−20

−10

100

110

x−position(m)

y−position(m)

UAVs and Target Locations

Figure 14: UAVs and target positions (time-varying delay

and packet loss case).

and maximum errors, comparing the nominal case to

the case with nonuniform constant delays. From the

ﬁgure, the average and maximum errors for the delay

case reach the value of zero after 200 seconds, taking

about 40 seconds more time than in the nominal case

to reach the desired conﬁguration. The presence of

time delays in the network does not prevent the agents

from reaching the desired conﬁguration; however, the

time delays increase the time it takes to reach the de-

sired conﬁguration.

Experiment 3: Data Dropouts. This experiment

demonstrates the effect of packet loss on the behav-

ior of the UAVs. A probabilistic model is used to im-

plement the loss of packets in the channels. For our

studies, we simulate the case of a ten percent prob-

ability of packet loss. Figure 11 shows the average

and maximum errors, comparing the nominal case to

the case of ten percent probability of packet loss. The

plot shows that even with ten percent packet loss, the

UAVs still manage to come very close to the desired

conﬁguration, demonstrating the resilience of the net-

work. Due to the packet loss, the UAVs will never

reach a steady state; however, the UAVs’ positions

end up within a maximum error of 6 meters and an

average error of 4 meters of the desired conﬁguration.

Experiment 4: Time-varying Delays. This experi-

ment demonstrates the effect of time-varying delays

on the behavior of the UAVs. To simulate the case

of time-varying delays, we incorporate a disturbance

node in the network. The sampling period of the dis-

turbance node is set to a value of 0.05 seconds, and

the disturbance node ﬂoods the network with distur-

bance packets based on a Bernoulli process with pa-

rameter d. The disturbance node samples a uniformly

distributed random variable X[k] ∈ [0,1] every 0.05

seconds. If X[k] > d, a disturbance packet is forced on

the network. Figure 12 shows the average and maxi-

mum errors, comparing the nominal case to the time-

varying delay case, with d = 0.5. The plot shows that

in the presence of time-varying delays, the UAVs re-

main stable and settle within a maximum error of 0.09

meters and an average error of 0.02 meters from the

desired conﬁguration.

Experiment 5: Combined Network effects. The

experiment demonstrates the combined effects of ten

percent packet loss and time-varying delays on the be-

havior of the UAVs. This experiment studies the com-

bined network effects of time-varying delays and data

loss in order to simulate the real world dynamics of

the network. Again, the time-varying delays are intro-

duced through the disturbance node with d = 0.5. Fig-

ure 13 shows the average and maximum errors, com-

paring the nominal case to the case with the combined

network effects. The ﬁgure shows that the average

and maximum errors increase slightly after appearing

to settle near 5 meters. This occurs because one of the

UAVs actually moves interior to the circle around the

target, shown in Figure 14. The UAV directly below

the target is approximately 15 meters away from its

desired location, and causes the maximum error seen

in Figure 13.

6 CONCLUSIONS

Discrete-time implementation of networked multi-

agent systems introduces signiﬁcant challenges

caused by effects such as network delays and data

loss. This paper proposes a passive-by-construction

distributed network control design framework that en-

sures l

-stability in the presence of these network ef-

fects. Using steady-state analysis, we show how to

control the agents in the multi-agent network in order

to establish an n-gon upon deployment. Simulations

supporting the theoretical results are presented on the

A PASSIVITY-BASED APPROACH TO DEPLOYMENT IN MULTI-AGENT NETWORKS

Simulink/TrueTime platform. In future work, we plan

to extend the design framework to achieve other group

oriented tasks such as output synchronization, forma-

tion control, and rendezvous. We will also extend the

work to formations in R

ACKNOWLEDGEMENTS

This work is supported in part by the National Sci-

ence Foundation (NSF CCF-0820088), the U.S. Army

Research Ofﬁce (ARO W911NF-10-1-0005), the

U.S. Air Force Ofﬁce of Scientiﬁc Research (MURI

FA9550-06-0312), the U.S Army Research Labo-

ratory (ARL W911NF-087-2-0004), and Lockheed-

Martin. The views and conclusions contained herein

are those of the authors and should not be interpreted

as necessarily representing the ofﬁcial policies or en-

dorsements, either expressed or implied, of the U.S.

Government.

REFERENCES

Arcak, M. (2007). Passivity as a design tool for group co-

ordination. IEEE Transactions on Automatic Control,

52(8):1380–1390.

Bai, H., Arcak, M., and Wen, J. T. (2008). Rigid body atti-

tude coordination without inertial frame information.

Automatica, 44(12):3170 – 3175.

Chopra, N., Berestesky, P., and Spong, M. (2008). Bilat-

eral teleoperation over unreliable communication net-

works. IEEE Transactions on Control Systems Tech-

nology, 16(2):304–313.

Fax, J. A. and Murray, R. M. (2004). Information ﬂow

and cooperative control of vehicle formations. IEEE

Transactions on Automatic Control, 49(9):1465 –

1476.

Godsil, C. and Royle, G. (2001). Algebraic Graph Theory.

Springer-Verlag New York, Inc.

Igarashi, Y., Hatanaka, T., Fujita, M., and Spong, M. (2008).

Passivity-based output synchronization in se(3). In

American Control Conference, pages 723–728.

Ihle, I.-A. F., Arcak, M., and Fossen, T. I. (2007). Passivity-

based designs for synchronized path-following. Auto-

matica, 43(9):1508 – 1518.

Kottenstette, N. and Antsaklis, P. (2007). Stable digital con-

trol networks for continuous passive plants subject to

delays and data dropouts. 46th IEEE Conference on

Decision and Control, pages 4433–4440.

Kottenstette, N., Hall, J., Koutsoukos, X., Antsaklis, P.,

and Sztipanovits, J. (2009). Digital control of mul-

tiple discrete passive plants over networks. Inter-

national Journal of Systems, Control and Communi-

cations (IJSCC): Special Issue on Progress in Net-

worked Control Systems. To Appear.

Kottenstette, N. and Porter, J. (2009). Digital Passive Atti-

tude and Altitude Control Schemes for Quadrotor Air-

craft. 7th International Conference on Control and

Automation.

Lawrence, D. A., Frew, E. W., and Pisano, W. J. (2008).

Lyapunov vector ﬁelds for autonomous uav ﬂight con-

trol. AIAA Journal of Guidance, Control, and Dynam-

ics, 31(5):1220–1229.

MathWorks, I. T. (2008). Simulink. Dynamic System Simu-

lation for MATLAB, Version 7.1.

Niemeyer, G. and Slotine, J.-J. E. (2004). Telemanipulation

with time delays. International Journal of Robotics

Research, 23(9):873 – 890.

Ohlin, M., Henriksson, D., and Cervin, A. (2007).

TrueTime 1.5 Reference Manual. Dept. of

Automatic Control, Lund University, Sweden.

http://www.control.lth.se/truetime/.

Olfati-Saber, R. (2006). Flocking for multi-agent dynamic

systems: algorithms and theory. IEEE Transactions

on Automatic Control, 51(3):401–420.

Olfati-Saber, R., Fax, J. A., and Murray, R. M. (2007). Con-

sensus and cooperation in networked multi-agent sys-

tems. Proceedings of the IEEE, 95(1):215–233.

Ren, W., Beard, R., and Atkins, E. (2005). A survey of con-

sensus problems in multi-agent coordination. In Pro-

ceedings of the American Control Conference, pages

1859–1864 vol. 3.

Stramigioli, S., Secchi, C., van der Schaft, A. J., and Fan-

tuzzi, C. (2005). Sampled data systems passivity and

discrete port-hamiltonian systems. IEEE Transactions

on Robotics, 21(4):574 – 587.

van der Schaft, A. (1999). L2-Gain and Passivity in Nonlin-

ear Control. Springer-Verlag New York, Inc., Secau-

cus, NJ, USA.

Wang, W. and Slotine, J.-J. (2006). Contraction analysis of

time-delayed communications and group cooperation.

IEEE Transactions on Automatic Control, 51(4):712–

717.

Zames, G. (1966). On the input-output stability of time-

varying nonlinear feedback systems part one: Con-

ditions derived using concepts of loop gain, conicity,

and positivity. IEEE Transactions on Automatic Con-

trol, 11(2):228–238.

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics