DYNAMIC MODELING AND PNEUMATIC SWITCHING CONTROL

OF A SUBMERSIBLE DROGUE

Y. Han, R. A. de Callafon, J. Cort´es

Department of Mechanical and Aerospace Engineering, UCSD, 9500 Gilman Drive, La Jolla, CA 92093-0411, U.S.A.

J. Jaffe

Scripps Institution of Oceanography, UCSD, 9500 Gilman Drive, La Jolla CA, 92093-0238, U.S.A.

Keywords:

Underwater robotics, Submersible drogues, Switching control.

Abstract:

This paper analyzes the dynamic properties of a submersible drogue for which buoyancy control is imple-

mented by a ﬂexible membrane and pneumatic actuation. It is shown how a simple on/off switching algorithm

tuned on the basis of depth measurements and an estimated depth velocity can be used to achieve accurate

depth control with small ﬂuctuations. The switching control makes the pneumatically controlled drogue an

inherent hybrid system and conditions for contraction and stability are given for the proposed switching con-

trol algorithm. Numerical evaluation of the conditions for stability and experimental data of the switching

control implemented on a pneumatic submersible drogue further demonstrates the soundness of the proposed

switching control algorithm.

1 INTRODUCTION

A compelling and unanswered need in oceanogra-

phy is to sample the (coastal) environment at high-

resolution spatial and temporal scales than presently

possible (Davis, 1991; Kunzig, 1996). Although cur-

rent systems have led to many important discover-

ies, oceanographers would agree that many funda-

mental processes are presently unobservable due to

the sparseness of current sampling geometries (Perry

and Rudnick, 2003; Schoﬁeld and Tivey, 2004). The

development of an oceanographic observatory system

based on small and inexpensive buoyancy-controlled

drogues that are able to perform motion control for

collective oceanographic measurements could allevi-

ate the problem of data sparseness.

One of the key requirements on (coordinated)

motion is to control the individual depth of such

buoyancy-controlled drogues. From a motion con-

trol point of view, alternating depth proﬁles can be

used for motion planning purposes when using glider

based propulsion (Fiorelli et al., 2003; Bhatta et al.,

2005; Paley et al., 2008). On the other hand, small

form factor buoyant objects can beneﬁt from strong

This work was partially supported by NSF Award

OCE-0941692.

horizontal shear layers typically observed in shallow

coastal ocean ﬂows (Helfrich and White, 2007; Ly

and Luong, 1997) to perform motion control by depth

planning. Buoyancy induced motion should be done

with as little control energy as possible to maximize

deployment time for scientiﬁc data acquisition pur-

poses. Requirements on energy storage are limited

due to the desire of a small form factor design to sim-

ulate a free ﬂoating, low Reynolds Lagrangian-based

distributed sensor system.

In this paper we will analyze the design of a single

small form factor buoyancy-controlled drogue. Proto-

types of buoyancy-controlled drogues are inspired by

current activities at Scripps Institute of Oceanography

(Colgan, 2006). Compared with these existing de-

signs, we propose a pneumatically controlled drogue

with a ﬂexible membrane. As shown in the analysis

of the dynamics, compressibility of the ﬂexible mem-

brane leads to an inherent unstable buoyancy equilib-

rium that requires very little control energy to gener-

ate alternating depth proﬁles. In addition, a separa-

tion of battery and pneumatic power reduces electric

power and actuator requirement for motion control.

We propose a simple switching (on/off) control al-

gorithm for the buoyancy control of the drogue. It

is shown how an on/off switching algorithm tuned

Han Y., A. de Callafon R., Cortés J. and Jaffe J. (2010).

DYNAMIC MODELING AND PNEUMATIC SWITCHING CONTROL OF A SUBMERSIBLE DROGUE.

In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 89-97

DOI: 10.5220/0002953800890097

 SciTePress

on the basis of depth measurements and an estimated

depth velocity proﬁle can be used to achieve accurate

depth control with small ﬂuctuations. The switching

control makes the pneumatically controlled drogue

an inherent hybrid system (Van der Schaft and Schu-

macher, 2000) and a formal result on contraction and

stability evaluated is given for the proposed control

algorithm. The formal result on stability is evaluated

numerically and both simulation and experimental

data of the switching control implemented on a pneu-

matic submersible drogue are included in this paper to

demonstrate the effectiveness of the proposed pneu-

matically switching buoyancy-controlled drogues.

2 ILLUSTRATION OF DESIGN

CONCEPT

Previous work at Scripps Institute of Oceanography

(Colgan, 2006) has illustrated the feasibility of build-

ing a standalone ball-shaped free-ﬂoating drogue ve-

hicle. A similar, but smaller, less expensive and po-

tentially more energy efﬁcient concept based on a

pneumatic controlled ﬂexible membrane attached to

the drogue is proposed in this paper for buoyancy con-

trol up to a depth of 150 feet. A prototype of the cylin-

drical shaped (1 liter in volume) membrane controlled

drogue is shown in Figure 1.

(a) (b)

Figure 1: Pneumatic membrane controlled cylindrical

shaped (a) drogue. Schematic inside view (b) of cylindri-

cal shaped drogue.

Similar ﬂexible membranes for pneumatic con-

trol of underwater drogues have also been used in

ARGO ﬂoats (Gould, 2003; Gould, 2004), but at a

much larger form factor. In these design concepts,

the membrane actuation is primarily used for provid-

ing the buoyancy control for surfacing of the drogues.

Instead, to conform to a small form factor design,

we use the displaced volume under the ﬂexible mem-

brane for both buoyancy control and the opportunity

to create alternating depth proﬁles that includes pe-

riodic surfacing. Due to the compressibility of the

membrane, the slightest perturbation in depth will

cause a change in volume and the equilibrium state

of the drogue is unstable. This is beneﬁcial for low

energy periodic surfacing control. As shown in this

paper, feedback control can be used to stabilize the

drogue to any desired depth.

3 DYNAMIC MODELING OF

PNEUMATIC DROGUE

3.1 Rigid Body Dynamics

Assuming a drag parameter d due to a drag force in

water, the depth x(t) of the drogue can be described

by the second order differential equation

m¨x(t) + sign( ˙x(t))d ˙x

(t) = F

−F

(t) (1)

where the constant rigid mass of the drogue and added

mass due to displacement of ﬂuid (Brennen, 1982) are

combined in the mass parameter m. In the equation

(1), F

is the downward (constant) gravitational force

= mg

and F

(t) is buoyancy force

(t) = ρg[V

(t) +V]

determined by the ﬁxed drogue volume V and the dis-

placed volume V

(t) under the membrane. The con-

stant ρ is the density of the water, which we assume to

be constant at different depths. The drag parameter d

is determined by the drag coefﬁcient c

of the drogue

moving in water at a low Reynolds number and typi-

cally given by

d =

ρA

where A denotes the frontal aerial surface of the

drogue. In the above equations, we consider V

(t) as

a control variable to control the depth of the drogue

using measurements of the depth x(t).

The condition of natural buoyancy at any depth

c ≥0 is determined by the initial conditions x(0) = x

and ˙x(0) = 0 for the differential equation given in (1)

and yields the desired (initial) volume

(0) = V

−V (2)

for natural buoyancy. Ideally, the mass m and the vol-

ume V of the drogue should be chosen to allow for a

Water density does depend on salidity and depth, but

these second order effects are neglected here

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

large range in V

(t) > 0 for buoyancy control. How-

ever, even small changes in V

(t) sufﬁce in generat-

ing motion of the drogue due to no-friction free body

movement of the drogue ﬂoating in water.

3.2 Actuator Dynamics

Using a pneumatic mechanism to add or bleed air

to effectively increase V

(t) induces additional (ac-

tuator) dynamics that needs to be taken into account

in order to design a control algorithm. The dis-

placed volume V

(t) under the membrane is a func-

tion of both the air ﬂow, the stiffness of the membrane

and the external pressure surrounding the membrane.

Considering a ﬂow φ(t) used to change the volume

(t) under the membrane, with the ideal gas equa-

tion (Fox et al., 2004) we see that the product of the

membrane pressure P

(t) and volumeV

(t) can be de-

scribed by

(t)V

(t) =



τ=0

φ(τ)dτ



RT(t) (3)

where n

indicates the number of gas molecules for

natural buoyancy at t = 0, R is the Boltzman constant

and T(t) is the gas temperature which we assume to

be known (measurable) for now. Finally, we assume

a linear increase of the membrane pressure P

(t) due

to changes in the volume V

(t) according to

(t) = k

(t) + P

(t), P

(t) = k

x(t) + P

(4)

where k

is the (linear) membrane membrane stiff-

ness and P

(t) models the effect of the external pres-

sure as the sum of the atmospheric pressure P

and

the product of the depth x(t) and the pressure depth

constant k

given by

= ρg

The last equation allows us to compute the unknown

in (3) at time t = 0 for which we have natural buoy-

ancy and φ(0) = 0. With the desired initial displace-

ment volume V

under the membrane given in (2), we

see that at an initial depth x(0) = x

> 0

(0) = k

+ k

+ P

, V

−V

allowing us to compute n

+ P

, V

−V

indicating quadratic dependency on the initial dis-

placed volume V

under the membrane due to the lin-

ear membrane stiffness k

and linear dependency due

to inﬂuence of the depth dependent pressure.

To complete the analysis, we still need an equa-

tion that describes the ﬂow φ(t). To anticipate the

switching control proposed in this paper, the ﬂow φ(t)

is modulated by three different switching states: in-

ﬂate, deﬂate or none. The input u can switch between

the values

u =







1 inﬂate

−1 deﬂate

0 none

can be used to distinguish between three different

switching states. Using the Bernoulli equation (Fox

et al., 2004) and assuming a steady incompressible

ﬂow, each state has a different ﬂow φ(t) that is mod-

eled via a proportional relationship with the square

root of the pressure difference:

φ(t) =











−P

(t) u = 1

−k

(t) −P

(t) u = −1

0 u = 0

where P

denotes the (constant) output pressure of

theCO

pressure regulator and k

, k

denote the valve

constants of respectively the add and bleed valves. If

both valves are the same, then k

= k

. With the

pressure relationship given in (4) we see that the gas

ﬂow φ(t) can now be modeled as

φ(t) =











−k

x(t) −k

(t) −P

−k

(t)

(5)

respectively for u = 1, u = −1 and u = 0. As a result,

membrane inﬂation and deﬂation will occur at dif-

ferent ﬂow rates. Membrane inﬂation is determined

mainly by the CO

pressure regulator, but pressure

build up due to depth and membrane stiffness (vol-

ume) has a negative inﬂuence. For deﬂation it can

be seen that only the membrane stiffness contributes

to a desired pressure difference and is independent of

depth.

3.3 Combined Dynamic Model

Combing the different equations and eliminating in-

termediate variables leads to a dynamic switching

system described by a set of coupled non-linear and

non-stiff ordinary differential equations (Hairer et al.,

1993) in depth x(t), volume V

(t) and gas ﬂow φ(t)

given by

¨x(t) = −sign(˙x(t))

˙x

(t) +

ρg

−V

(t))

(t)

+ [k

x(t) + P

(t) =



τ=0

φ(τ)dτ



RT(t)

DYNAMIC MODELING AND PNEUMATIC SWITCHING CONTROL OF A SUBMERSIBLE DROGUE

φ(t) =











−k

x(t) −k

(t) −P

u = 1

−k

(t) u = −1

0 u = 0

where a summary of the meaning of the physical pa-

rameters is given in Table 2 in the Appendix of this

paper. For analysis purposes, the above dynamical

model is written in a short hand notation

˙z(t) = f

(z(t)) (6)

where z(t) = [x(t) ˙x(t) φ(t)]

combines the state vari-

ables and f

(z) for u ∈{ −1,0, 1}denotes the different

dynamic behavior of the system as a function of the

switching signal u. Simulations of the dynamics can

be done along with the initial conditions

z(0) =





x(0)

˙x(0)

φ(0)













and the resulting initial number of gas molecules n

and volume given V

+ P

−V

(7)

It can be observed from the above equations that the

membrane gas temperature T or density parameter ρ

can be considered as a time or depth varying param-

eters that inﬂuences the dynamics of the system. The

switching signal u ∈ {−1,0,1} is the control input

signal available to provide depth tracking and stabi-

lization for the drogue.

4 EQUILIBRIUM AND

STABILITY ANALYSIS

Equilibrium conditions for the drogue can be studied

by setting the ﬂow rate φ(t) = 0 and the switching

signal u = 0, reducing the differential equations to

¨x(t) = −sign( ˙x(t))

˙x

(t) +

ρg

−V

(t))

(t)

+ [k

x(t) + P

(t) = n

RT(t)

(8)

Due to the assumptions of an ideal gas and lin-

ear membrane stiffness k

, the volume V

(t) can be

solved explicitely from the resulting quadratic equa-

tion as a function of depth x(t) and temperature T(t).

This yields a single solution under the constraint

(t) > 0 given by

(t) = −

x(t) + P

]

+ 4k

RT(t)

(9)

With T(t) = T

and both x(t), V

(t) > 0 and n

given

in (7) it can be seen that the solution

x(t) = x

> 0

˙x(t) = 0

(t) = V

−V > 0

is a stationary point of the equation in (8) as V

(t)

satisﬁes

−

+ P

]

+ 4k

+ P

−

+ P

(2k

+ [k

+ P

])

= V

known as neutral buoyancy of the drogue at depth x

However, the stationary point is an unstable equilib-

rium as any perturbation on x(t) = x

causes an un-

bounded x(t), physically indicating that the drogue

will either surface or sink without control. Such dy-

namic behavior is due to the compressibility of the

membrane and can be used favorably to surface with-

out little or no control energy.

The instability of the equilibrium can be shown

by considering a perturbation on the depth x(t) > 0 at

time t = t

given by ¨x(t

) = 0 and x(t

) = x

+ ε, ε >

0. Due to this small increase in depth,

) = −

+ ε) + P

]

+ 4k

= −

+ P

] −

ε+ δ

where δ is given by the expression

+ P

]

+ 4k

+ k

+ 2k

+ P

)ε

With 4k

> 0, the strict inequality

δ <



+ P

]

+ 4k

+ k



where



+ P

]

+ 4k

+ k



+ P

]

+ 4k

+ k

indicates that

) < −

+ P

]

+ 4k

= V

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

making the displaced volume V

) under the mem-

brane smaller than V

due to x(t

) = x

+ ε. With

−V

)) > 0 and ¨x(t

) = 0, the differential equa-

tion for x(t) in (8) indicates ˙x(t

) > 0 causing a further

increase of the depth x(t) for t > t

. This indicates

the increase of the depth x(t) (sinking) and the insta-

bility of the neutral buoyancy operating point of the

drogue at x(t) = x

. A similar argument can be given

for a perturbation x(t

) = x

−ε that will result in a de-

crease in the displaced volume V

) under the mem-

brane, causing the drogue to surface. The stability

analysis indicates that neutral buoyancy is obtained

only at one speciﬁc (initial) depth x

such that V

(t)

given in (9) satisﬁes V

(t) = V

= m/ρ−V to provide

a buoyancy force that balances the gravitational force.

5 DEPTH SWITCHING

CONTROL

Although the compressibility of the membrane can be

used favorably to surface or sink the drogue without

little or no control energy, a contraction or stabiliza-

tion algorithm towards a target depth reference r(t)

must be implemented via feedback control. Due to the

switching behavior of the control signal u∈{−1, 0,1}

we can only expect to obtain depth tracking and neu-

tral buoyancy within a user speciﬁed tolerance level

α around the depth reference r(t). Our objective is to

design a switching control algorithm that guarantees

attaining the depth region |x(t) −r(t)| < α from an

arbitrary initial depth condition x

In this paper this is achieved by simply modulat-

ing the switching signal u ∈ {−1,0,1} on the basis of

feedback information of the depth x(t) and the depth

velocity ˙x(t). With a target depth r(t) > 0 and a γ

with 0 < α < γ, the depth measurements are classiﬁed

in three different regions that are pairwise disjoint

= {x | γ < |r(t) −x|}

= {x | α < |r(t) −x| ≤ γ}

= {x | |r(t) −x| ≤ α}

(10)

respectively denoted by the attraction region R

, the

stabilization region R

and the tolerance region R

We will ﬁrst summarize the proposed switching con-

trol algorithm. Subsequently we provide a proposi-

tion that shows how contraction to a speciﬁc depth

region can be obtained.

Algorithm 1. Let R

, j = 1, 2,3 be the depth region

deﬁned in (10) where 0 < α < γ and consider the max-

imum drogue velocities β

for each region R

where

≤ β

and let

σ = sign(r(t) −x(t)) ∈ {−1,1}

Default, the switching signal u = 0 but will be either

u = 1 (add air to increase the volumeV

(t)) or u = − 1

(bleed air to reduce V

(t)) according to the following

rules:

1. If x(t) ∈R

, consider the two situations:

a. If |˙x(t)| ≤ β

then u = −σ (increase depth ve-

locity)

b. If σ · ˙x(t) < 0 then u = −σ (velocity in wrong

direction, increase/decrease depth velocity di-

rectly)

2. If x(t) ∈R

, consider the two situations:

a. If |˙x(t)| > β

and σ · ˙x(t) > 0 then u = σ (de-

crease velocity)

b. If σ · ˙x(t) < 0 then u = −σ (velocity in wrong

direction, increase/decrease depth velocity di-

rectly)

3. If x(t) ∈ R

and |˙x(t)| > β

then u = sign{˙x(t)}

(chatter input signal to achieve velocity bound)

As can be seen from the above algorithm, each

region R

, j = 1,2,3 has speciﬁc bounds β

on the

depth velocity ˙x(t) that determines the modulating of

the switching signal u ∈ {−1,0,1}. The attraction re-

gion R

is used to give the drogue the right velocity

with a maximum of β

to attract it in the stabilization

region R

. When the drogue enters the region R

, the

velocity is reduced to β

to avoid abrupt entering and

exiting of R

and providing an entering velocity of

for the tolerance region R

. Obviously, the choice

of β

is closely related to the size of γ. As soon as

the drogue enter the tolerance region R

the control

can be turned off by choosing β

= β

as the entering

velocity will be β

. Choosing β

< β

allows an ad-

ditional reduction of drogue velocity within the toler-

ance region at the price of a chattering control signal.

The proposed switching control in Algorithm 1 is

motivated by the need to dampen the (unstable) rigid

body motion of the drogue and maintain neutral buoy-

ancy. The proposed algorithm is basically a Propor-

tional and Derivative (PD) control architecture with

speciﬁc level sets for position x(t) and velocity ˙x(t)

measurements. It should be observed that feedback

information on x(t) and ˙x(t) is required to implement

the proposed control algorithm. However, ˙x(t) can

be approximated by discrete-time sampling and ﬁlter-

ing of the depth x(t), allowing a discrete-time imple-

mentation of the switching control algorithm based on

depth measurements only.

DYNAMIC MODELING AND PNEUMATIC SWITCHING CONTROL OF A SUBMERSIBLE DROGUE

6 HYBRID STABILITY ANALYSIS

For the analysis of the proposed switching control

algorithm, the framework of hybrid systems analy-

sis (Van der Schaft and Schumacher, 2000; Liberzon,

2003; Goebel et al., 2009) can be used to prove stabil-

ity properties of the resulting control system. Based

on the switching control law proposed in Algorithm 1,

the behavior of the drogue is modeled as a hybrid sys-

tem with three different modes corresponding to in-

ﬂation for u = 1, deﬂation for u = −1, and a neutral

mode for u = 0.

Each mode has its active region and these regions

share switching surfaces with each other. The tran-

sition between modes occurs when the system trajec-

tory crosses these switching surfaces. In this paper,

a multiple Lyapunov functions based parameter de-

pendent switching strategy is used to investigate the

stability of the proposed switching control algorithm

for the buoyancy control of the drogue.

In order to establish an active region for each actu-

ator dynamic mode, three Lyapunov functionsV

, u ∈

{−1, 0,1} must be deﬁned. The three quadratic Lya-

punov functions V

are deﬁned as follows:

(−(x−r) −10˙x+ φ)

inﬂation

−1

(−(x−r) −10˙x+ φ)

deﬂation

(x−r)

˙x

neutral

(11)

Subsequently, the stability analysis is based on a the-

orem in (Branicky, 1998) on Lyapunov stability of

switched and hybrid systems and summarized in the

following result for the switched hybrid system con-

sidered in this paper.

Proposition 1. Consider the system ˙z(t) = f

(z(t)) in

(6) and let V

be the Lyapunov functions given in (11)

for u ∈ {−1, 0,1}. Let L

be the Lie derivative

of V

along the vector ﬁeld spanned by the subsystem

(·). The origin of the system is asymptotically stable

if the following two conditions are satisﬁed

(a) L

< 0 for each u ∈ {−1,0,1}

(b) V

is nonincreasing along switching

times on the uth system ˙z(t) = f

(z(t))

(12)

In this paper we use numerical analysis to ver-

ify the two conditions (12) in Proposition 1. It can

be veriﬁed that each Lyapunov function V

for u ∈

{−1, 0,1}in (11) is positive deﬁnite over its active re-

gion characterized by L

< 0. To characterize (12)

over the three dimensional state vector z = [x ˙x φ]

Lyapunov analysis is conducted by varying φ in the

admissible range. This can be done as φ is not used

directly in the switching control of Algorithm 1. Nu-

merical evaluation of (12) for different values of φ

is done using a non-stiff differential equation solver

(Cooper, 2004) and implemented via

ode45

in Mat-

lab.

For the inﬂation mode, L

for φ = 0 is plotted

in Figure 2 and the active region for which (12) holds

is separated by a dashed line, whereas the arrows indi-

cate a decreasing value of V

. If φ is varied, the whole

solution surface moves through the φ-axis (perpendic-

ular to x− ˙x plane) resulting in the shift of the active

region along the ˙x-axis. The same analysis can be

done for other modes. A similar plot is created for the

deﬂation mode where L

−1

for φ = 0 is plotted in

Figure 3 and the neutral mode where L

for φ = 0

is plotted in Figure 4.

Depth

Velocity

−0.5

−0.4

−0.3

−0.2

−0.1

0.1

0.2

0.3

0.4

0.5

<0 (active region)

Figure 2: The active region of the inﬂation mode. The ar-

rows indicate the allowable direction of solution trajectory.

In inﬂation mode, the solution trajectory always follows this

allowable direction.

Depth

Velocity

−0.5

−0.4

−0.3

−0.2

−0.1

0.1

0.2

0.3

0.4

0.5

f−1

−1

<0 (active region)

f−1

−1

Figure 3: The active region of the deﬂation mode. The ar-

rows indicate the allowable direction of solution trajectory.

In deﬂation mode, the solution trajectory always follows

this allowable direction.

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

Depth

Velocity

−0.5

−0.4

−0.3

−0.2

−0.1

0.1

0.2

0.3

0.4

0.5

(active region)

Figure 4: The active region of the neutral mode. The ar-

rows indicate the allowable direction of solution trajectory.

In neutral mode, the solution trajectory always follows this

allowable direction.

Table 1: Numeric parameters of dynamic drogue model for

non-linear simulation of switching control algorithm.

symbol value units

V 10

−3

m 1.5 kg

d 30 N/m

ρ 1.03·10

kg/m

g 9.81 m/s

5·10

Pa/m

or N/m

288 K

R 8.314472 (m

Pa)/(K mol)

−4

mol/

√

−4

mol/

√

Pa or N/m

10 m

Based on these ﬁgures, the existence of a stability

region characterized by (12) can be veriﬁed. There-

fore, the proposed hybrid control strategy using the

active regions and switching surfaces stabilizes the

drogue system.

7 SIMULATION RESULTS

To illustrate the performance of the switching control

in Algorithm 1, the controlled dynamic behavior of a

model of a buoyancy controlled submersible drogue

is simulated. The model is based on the set of cou-

pled non-linear differential equations given in (6) and

based on the numerical parameters listed in Table 1.

A summary of the meaning of the physical parameters

is given in Table 2 in the Appendix of this paper.

Using the switching control summarized in Algo-

rithm 1 with the regions of (10) based on a depth toler-

ance α = 0.5m and a stabilization region speciﬁed by

γ = 2α = 1m and a maximum velocity β

= 0.3m/s in

region R

and a maximum velocity β

= β

= 0.1m/s

in region R

and R

, the performance of the switching

control algorithm can be evaluated by the simulation

results depicted in Figure 5. The results were com-

puted by numerically solving the non-stiff differential

equations of the ODE’s of the model of the drogue

using an implementation of the explicit Runge-Kutta

(4,5) pair implemented in

ode45

in Matlab (Shampine

and Reichelt, 1997).

0 20 40 60 80 100 120

Result of closed−loop (full state feedback) simulation of drogue

depth [m]

reference depth [m]

0 20 40 60 80 100 120

−1

−0.5

0.5

time [sec]

depth velocity [m/s]

bladder volume [liter]

control input [−1,0,1]

Figure 5: Simulation results of switching control Algo-

rithm 1 with α = 0.5m, γ = 1m, β

= 0.3m/s and β

= 0.1m/s when the target depth references r(t) changes

from 10m to 30m at t = 5sec. The numerical values for

the drogue model used during this simulation are listed in

Table 1.

During the simulation the target depth r(t) of 10m,

for which the drogue is initially neutrally buoyant, is

changed to 30m at t = 5sec. It can be seen from the

simulation results in Figure 5 that the drogue stays

within approximately ±αm of the a constant target

depth, whereas a change to a different target depth is

accomplished with a maximum speed of β

= 0.3m/s

and only requires a few switches of the control signal

u. During steady state operation only very short actu-

ation of either the ”add” (u = 1) or ”bleed” (u = −1)

valves are used to maintain depth within the speci-

ﬁed tolerance region α and stabilization region γ. The

simulation conﬁrms the hybrid stabilization results.

DYNAMIC MODELING AND PNEUMATIC SWITCHING CONTROL OF A SUBMERSIBLE DROGUE

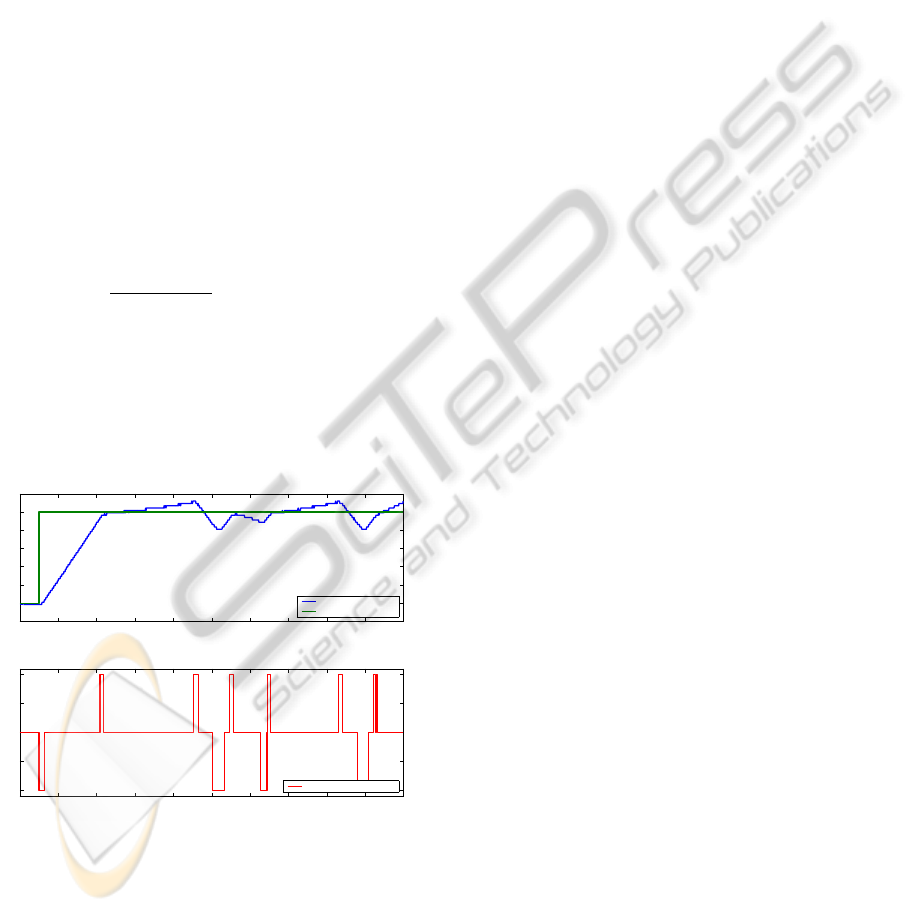
8 EXPERIMENTAL RESULTS

In an initial testing phase, the proposed control al-

gorithm was implemented on the pneumatic mem-

brane controlled cylindrical shaped drogue depicted

in Figure 1(a). The drogue design uses an internally

stored standard compressed 16 gram CO

cartridge

with a regulator assembly to change the displaced vol-

ume under the latex or neopropene membrane via two

small form factor Numatics series solenoid valves.

One valve is used for inﬂating the membrane, the

other valve is to bleed the CO

from the membrane.

The electrical components are powered by three

3.7Volt, 2700mAH Li-Ion batteries. A model 85 Ul-

tra Stable Pressure Sensor is used for depth measure-

ments measured by a 10bit AD converter on a Mi-

crosystems PIC18F4620 microprocessor.

The embedded control of the pneumatically con-

trolled drogue only uses depth measurements x(t)

sampled at 10Hz and depth velocity estimates v(t) are

obtained via

v(t) =

(t) −x

(t)

∆

, x

(t) = F(q)x(t)

where F(q) is a second order Butterworth ﬁlter with

a normalized cut-off frequency of 0.1 (1Hz). Both the

depth measurements x(t) and the control signal u(t)

as a function of the discrete-time t were saved for val-

idation purposes and the results of the experimental

work is summarized in Figure 6.

0 10 20 30 40 50 60 70 80 90 100

−1

−0.5

0.5

time [sec]

depth [m]

reference depth [m]

switching control signal

Figure 6: Preliminary experimental results of switching

control Algorithm 1 with α = 0.5m, γ = 1, β

= 0.3m/s and

= β

= 0.2m/s applied to the pneumatic membrane con-

trolled cylindrical shaped drogue depicted in Figure 1(a).

The target depth references r(t) changes from 10m to 15m

at t = 5sec.

The experimental results conﬁrm the stability of

the control algorithm for the pneumatic membrane

cylindrical shaped drogue even for the discrete-time

implementation of the algorithm. The slightly larger

values of β

and β

, chosen due to the noise lev-

els on the estimated velocity v(t), cause larger ve-

locity swings in the stabilization and tolerance re-

gion. Moreover the quantization effects of the depth

measurements based on a 10bit AD converter also

cause resolution limiations on the velocity estimate.

It can be seen that a larger value for β

requires more

switching for stabilization. Tuning of the controller

parameters α, γ, β

and β

can be used to further im-

prove the controller performance.

9 CONCLUSIONS

The dynamic properties of a submersible drogue for

which buoyancy control is implemented by a ﬂexible

membrane can be described by a set of coupled non-

linear and non-stiff ordinary differential equations. It

is shown that the compressibility of the membrane

leads to an dynamically unstable dynamical system

in terms of the depth, which can be used favorably to

surface or sink the drogue without little or no control

energy.

The instability does require a contraction or sta-

bilization algorithm to maintain a target depth refer-

ence. In this paper it is shown that a simple pneu-

matic on/off switching control algorithm in which

compressed CO

is either added or extracted from the

membrane actuator on the basis of three different and

pairwise disjoint depth regions can be used to stabi-

lize the depth positioning of the drogue.

The switching control algorithm leads to a hybrid

dynamical system, for which stability analysis results

are summarized in the paper. Numerical evaluation

of the stability conditions reveal that the proposed

on/off switching control algorithm leads to a stabi-

lized buoyancy-controlled drogue. Both simulation

and experimental studies indicate stability properties

and depth tracking performance within a speciﬁed tol-

erance levels.

REFERENCES

Bhatta, P., Fiorelli, E., Lekien, F., Leonard, N. E., Paley, D.,

Zhang, F., Bachmayer, R., Davis, R. E., Fratantoni,

D. M., and Sepulchre, R. (2005). Coordination of an

underwater glider ﬂeet for adaptive ocean sampling.

In International Workshop on Underwater Robotics,

Int. Advanced Robotics Programmed (IARP), Genoa,

Italy.

Branicky, M. (1998). Multiple Lyapunov functions and

other analysis tools for switched and hybrid systems.

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

IEEE Transactions on Automatic Control, 43:475–

482.

Brennen, C. (1982). A review of added mass and ﬂuid in-

ertial forces. Technical Report CR82.010, Naval Civil

Engineering Laboratory.

Colgan, C. (2006). Underwater laser shows. Explorations,

Scripps Institution of Oceanograhpy, 12:20–27.

Cooper, J. (2004). An Introduction to Ordinary Differential

Equations. Cambridge University Press.

Davis, R. (1991). Observing the general circulation with

ﬂoats. Deep-Sea Research, 38:531–571.

Fiorelli, E., Bhatta, P., Leonard, N. E., and Shulman, I.

(2003). Adaptive sampling using feedback control of

an autonomous underwater glider ﬂeet. In Proceed-

ings 13th International Symposium on Unmanned Un-

tethered Submersible Technology, Durham, NH.

Fox, R., McDonald, A., and Pritchard, P. (2004). Intro-

duction to Fluid Mechanics. John Wiley & Sons Inc.,

Hoboken, NJ, U.S.A.

Goebel, R., Sanfelice, R. G., and Teel, A. R. (2009). Hybrid

dynamical systems. IEEE Control Systems Magazine,

29:283.

Gould, J. (2004). Argo proﬁling ﬂoats bring new era of in

situ ocean observations. Earth and Ocean Sciences,

85(11).

Gould, W. J. (2003). WOCE and TOGA - the foundations

of the global ocean observing system. Oceanography,

Special Issue on Ocean Observations, 16(4):24–30.

Hairer, E., Nørsett, S. P., and Wanner, G. (1993). Solving

Ordinary Differential Equations I: Nonstiff Problems.

Springer Verlag, Berlin.

Helfrich, K. and White, B. (2007). Rapid gravitational

adjustment of a horizontal shear layer. In American

Physical Society, 60th Annual Meeting of the Divison

of Fluid Dynamics.

Kunzig, R. (1996). A thousand diving robots. Dis. Mag.,

17:60–63.

Liberzon, D. (2003). Switching in Systems and Control.

Systems & Control: Foundations and Applications se-

ries. Birkhauser, Boston.

Ly, L. N. and Luong, P. (1997). A mathematical coastal

ocean circulation system with breaking waves and nu-

merical grid generation. Applied Mathematical Mod-

elling, 21:633–641.

Paley, D., Zhang, F., and Leonard, N. E. (2008). Cooper-

ative control for ocean sampling: The glider coordi-

nated control system. IEEE Transactions on Control

Systems Technology, 16:735–744.

Perry, M. and Rudnick, D. (2003). Observing the ocean

with autonomous and lagrangian platforms and sen-

sors (ALPS): The role of ALPS in sustained ocean

observing systems. Oceanography, 4:31–36.

Schoﬁeld, O. and Tivey, M. (2004). Building a window to

the sea: Ocean research interactive observatory net-

works (ORION). Oceanography, pages 113–120.

Shampine, L. F. and Reichelt, M. W. (1997). The Matlab

ODE suite. SIAM Journal on Scientiﬁc Computing,

18:1–22.

Van der Schaft, A. and Schumacher, H. (2000). An Intro-

duction to Hybrid Dynamical Systems. Lecture Notes

in Control and Information Sciences 251, Springer-

Verlag.

APPENDIX

Table 2 summarizes the symbols use in the derivation

of the dynamical model of the drogue in Section 3.3.

Table 2: Summary of symbolic parameters of dynamic

drogue model.

symbol meaning

V volume of drogue

m mass of drogue

d drag parameter in water

ρ density of sea water

g gravitational constant

linear membrane stiffness

temperature of water

R gas constant

‘add air’ valve constant

‘bleed air’ valve constant

regulated CO

pressure

atmospheric pressure

depth for neutral buoyancy

DYNAMIC MODELING AND PNEUMATIC SWITCHING CONTROL OF A SUBMERSIBLE DROGUE