
EVALUATING MAXIMUM TRANSMISSION UNRELIABILITY
IN PERSISTENT CSMA PROTOCOL
Dariusz Kościelnik and Marek Miśkowicz
Department of Electronics, AGH University of Science and Technology, Al. Mickiewicza 30, Cracow, Poland
Keywords: Carrier Sense Multiple Access, Performance Analysis, Analytical Modelling.
Abstract: The paper addresses the problem of evaluating the unreliability of transmission, undertaken by a given
station, according to the persistent CSMA scheme. The unreliability of transmission is considered on the
media access control level so it is defined by the probability that a given node participates in a collision. The
presented results show that the maximum transmission unreliability is upper bounded by the persistence
level (p), which is the main parameter of the protocol. The presented analysis is compared to the
corresponding results for the non-persistent CSMA. As shown, both results are complementary because the
maximum transmission unreliability in the non-persistent CSMA scheme is also bounded by the probability
of choosing a single slot in the contention window.
1 INTRODUCTION
Although the carrier sense multiple access (CSMA)
protocols have been introduced in the early 70s, due
to their inherent flexibility and simplicity, they are in
more advanced versions still widely used in
contemporary networking, especially for wireless
communication (e.g., Tay, Jamieson, Balakrishnan,
2004). In particular, the predictive CSMA protocol
is employed in Local Operating Networks
(LonWorks) commercial platform for sensor and
control networking (Miśkowicz, Golański, 2006).
On the other hand, the non-persistent CSMA scheme
with a geometric distribution has been recently
proposed for sensor networking (Tay, Jamieson,
Balakrishnan, 2004; Miśkowicz, 2009a; Egea-López
et al., 2007).
The performance of the CSMA protocols have
been investigated intensively for decades. The main
criterion of performance analyses is evaluating the
throughput-delay characteristics (Kleinrock, Tobagi,
1975; Lam, 1980), or the protocol energy efficiency
in the context of wireless networking (Bruno, Conti,
Gregori, E., 2002; Calì, Conti, Gregori, 2000).
Most of the performance analyses are based on
classical approaches where the network load is
assumed to contain an infinity number of stations
that collectively produce (including both new and
retransmitted packets) the traffic with Poisson
arrivals (Kleinrock, Tobagi, 1975; Lam, 1980).
The Poisson model is an approximation of a
large but finite population in which every station
generates messages infrequently and each message
can be successfully transmitted a long time before
the station generates a next message.
The Poisson traffic model, based on the
fundamental assumption of stochastically distributed
independent stimuli, has been applied widely for
performance evaluation of computer networks.
Since the assumption of lightly loaded network is
invalid in many load scenaria in wireless local area
networks (Bruno, Conti, Gregori, 2002; Calì, Conti,
Gregori, 2000; Bianchi, 1998), and especially in
networked sensor and control systems (Miśkowicz,
2009b), the other class of performance analyses deal
with the load scenario of finite number of active
stations in which every station may produce a
significant portion of network traffic. In order to
model the network operation under heavy load, it is
assumed that all the stations are in the asymptotic
(saturation) conditions where they have always a
packet ready for transmission.
The present study deals with the performance
analysis of the persistent CSMA protocol that
belongs to one of generic CSMA schemes
introduced in (Kleinrock, Tobagi, 1975). The paper
contribution is the analytical proof that the
unreliability of transmission undertaken by a given
station, according to the persistent CSMA scheme, is
182
Ko
´
scielnik D. and Miskowicz M. (2010).
EVALUATING MAXIMUM TRANSMISSION UNRELIABILITY IN PERSISTENT CSMA PROTOCOL.
In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 182-186
DOI: 10.5220/0002958301820186
Copyright
c
SciTePress

upper bounded by the persistence level (p), which is
the main parameter of the protocol.
The unreliability of transmission is considered on
the media access control level so it is defined by the
probability that a given node participates in a
collision. The presented analysis is compared to the
corresponding results for the non-persistent CSMA.
As interesting, both results are complementary
because the maximum transmission unreliability in
the non-persistent CSMA scheme is also bounded by
the probability of choosing a single slot in the
contention window (Miśkowicz, Kościelnik, 2010).
The authors believe that the presented results
contributes to better understanding of the persistent
CSMA operation. To the best authors’ knowledge,
these results have not been yet published.
The performance analysis stated in the present
paper belongs to the studies of persistent CSMA
scheme for the network staying in the asymptotic
conditions because the evaluation of the maximum
transmission unreliability needs to feed a channel
with heavy load.
2 ANALYTICAL MODEL OF
PERSISTENT CSMA
2.1 Persistent CSMA Specification
The persistent CSMA scheme belongs to the slotted-
CSMA protocol where the channel idle time is
divided into fixed length intervals. All the stations in
the network are synchronized and forced to start a
transmission only at the beginning of a slot.
In the network that operates according to the
persistent CSMA, when a station has a new message
to transmit, it senses the channel. If the channel is
detected to be idle, then it transmits a message with
the probability p, while with probability 1-p, it
delays the message transmission to the next time
slot. The slot duration is determined by the network
propagation delay.
By a comparison, in the non-persistent CSMA,
when the station senses the channel to be idle, it
draws a number of a slot from a set of slots included
in the contention window. The probability
distribution of a random slot selection is uniform.
In the persistent CSMA protocol, the number of
empty slots preceding a (successful or unsuccessful)
transmission of a data packet is theoretically
unbounded because the probability of starting
transmission is defined by the geometric distribution
where a success occurs with the probability p, and a
failure with the probability (1-p). The mean number
of trials undertaken by a given station equals 1/p. On
the other hand, in the non-persistent CSMA
protocol, the maximum number of empty slots
before (successful or unsuccessful) transmission of a
data packet equals (W-1), and the mean number
(W-1)/2 where W is a number of slots in the
contention window.
2.2 Collision Probability in Single
Transmission Attempt
The probability
)(
)1(
k
coll
p
that a certain station is
involved in collision in the kth transmission attempt
is defined by the product of the following
probabilities:
)(
)12(
)(
)11(
)(
)1(
k
coll
k
coll
k
coll
ppp =
(1)
where
)(
)11(
k
coll
p
is the probability that all the
contending stations had not started the transmission
in the previous 1,…,k-1 transmission attempts, and
)(
)12(
k
coll
p
is the probability that at least one from the
s=1,2,3,… contending stations apart from a selected
station starts the transmission in the kth transmission
attempt. The former probability
)(
)11(
k
coll
p
is given by
the formula:
() ()
)1)(1(
1
1
1
)(
)11(
11
−+
−
=
+
−=−=
∏
ks
k
x
s
k
coll
ppp
(2)
The latter probability
)(
)12(
k
coll
p
is defined as follows:
()
∑
=
−
−=
s
x
xs
xx
s
k
coll
ppCpp
1
)(
)12(
1
(3)
where
(
)
]!
s
s
x
s
x
p
p
p
p
C
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
∑
=
1
11
0
(6)
As follows from (3), the probability
)(
)12(
k
coll
p
does not depend on
k but only on the number of
contenders
s. On the other hand, the probabilities
)(
)11(
k
coll
p (see (2)), and consequently
)(
)1(
k
coll
p also (see
(5)), is a decreasing function of the number
transmission attempt
k.
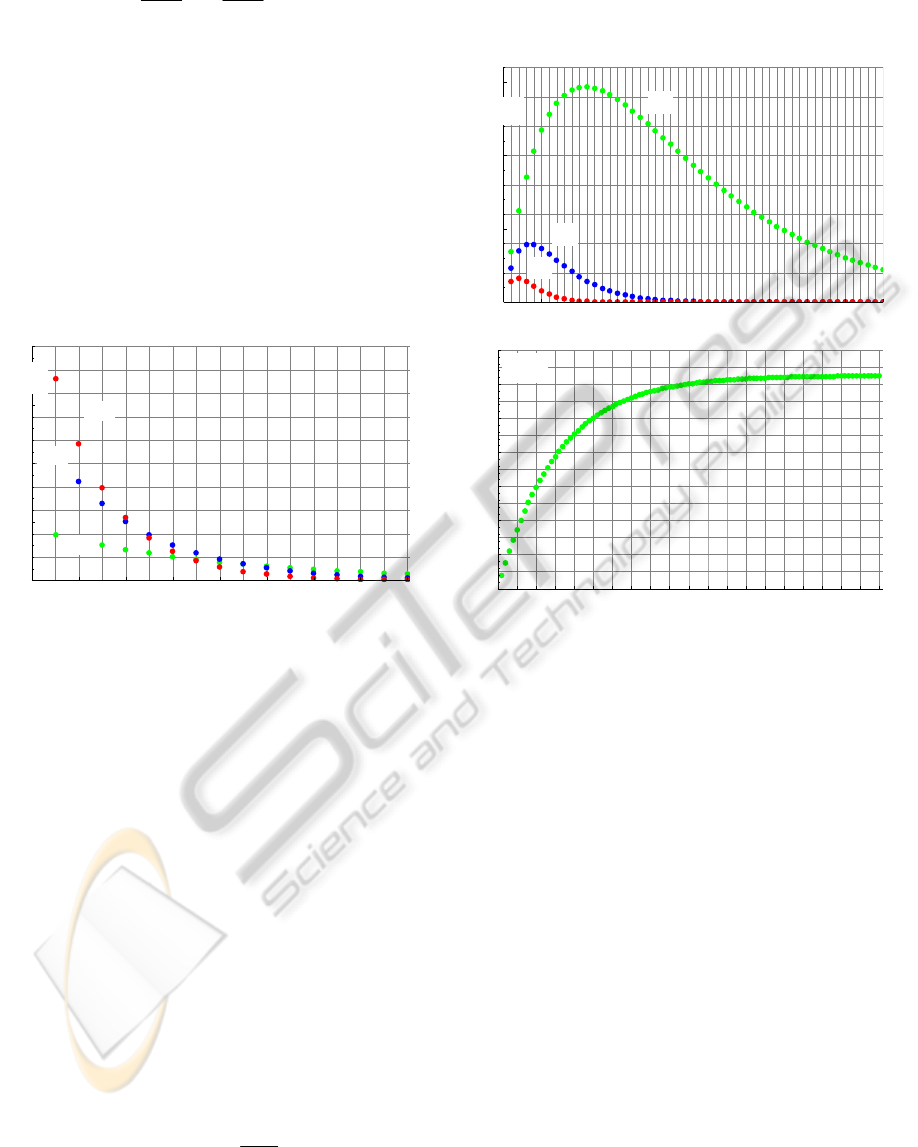
In Fig. 1, the plot of the probability
)(
)1(
k
coll
p
versus the number of transmission attempt
k for
selected numbers of the contending stations
s={1,3,5} for p=1/16 according to (5) is shown.
0 2 4 6 8 10 12 14 16
k
0.000
0.005
0.010
0.015
0.020
p
Figure 1: The probability
)(
)1(
k
coll
p
that a certain station is
involved in collision in the kth transmission attempt versus
the number k for various population sizes of the
contending stations s according to (5) for p=1/16 and
s={1,3,5}.
In Fig. 2(a,b), the plots of the probability
)(
)1(
k
coll
p
versus the number of the contending stations
s in
selected transmission attempts
k;k={1,2,5,9}
according to (5) are presented.
As seen in Fig. 2a, the probability
)(
)1(
k
coll
p that a
given station participates in collision for
k≥2 is a
unimodal function of
s that is maximized for a
certain number of contending stations
)(
0
k
s . The
)(
0
k
s is a decreasing function of k,k≥2. Instead, for
k=1, the
)(
)1(
k
coll
p increases strictly with s and
approaches a horizontal asymptote
pp
k
coll
=
)(
)1(
as
may be analytically derived (Fig. 2b):
()
p
p
p
ppp
s
s
s
coll
s
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−
⋅−=
∞→∞→
11
1
1limlim
)1(
)1(
(7)
In particular,
)(
)1(
k
coll
p reaches 0.0625 for
p=1/16=0.0625 for high s as seen in Fig.2b.
0 5 10 15 20 25 30 35 40 45 50
s
0.000
0.005
0.010
0.015
0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100
s
0.00
0.01
0.02
0.03
0.04
0.05
0.06
0.07
Figure 2: The probability
)(
)1(
k
coll
p
versus the population of
the contending stations s for p=1/16=0.0625 and selected
transmission attempts k={2,5,9} (a), and k={1} (b).
3 MAXIMUM TRANSMISSION
UNRELIABILITY IN
PERSISTENT CSMA
As stated, the probability
)(
)1(
k
coll
p that a certain
station is involved in collision in the
kth
transmission attempt is defined by the formula (5).
The total probability
)1(
)1(
k
coll
p
÷
that a certain station
participates in collision at most at the
kth
transmission attempt is defined as a sum:
∑
=
÷
=
k
x
x
coll
k
coll
pp
1
)(
)1(
)1(
)1(
(8)
where
)(
)1(
k
coll
p
is defined by (5).
By setting (5) to (8):
b)
a)
)(
)1(
k
col
l
p
k=5
k=2
k=9
)(
)1(
k
coll
p
s
=1
s
=5
s
=3
)1(
)1(coll
p
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
184

()
∑
=
+−+
÷
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−=
k
x
s
sxs
k
coll
p
ppp
1
)1)(1(
)1(
)1(
1
1
1
1
(9)
The probability
)1(
)1(
k
coll
p
÷
in the formula (9) is
defined as a geometric series with the first term
equal to
()
]11[
s
pp −− , and the ratio equal to
()
1
1
+
−
s
p so it might be computed as:
()
(
)
()
(
)
1
)1(
)1(
)1(
)1(1
1111
+
+
÷
−−
−−−−⋅
=
s
kss
k
coll
p
ppp
p
(10)
The plot of the probability
)1(
)1(
k
coll
p
÷
versus k
according to (10) is shown in Fig. 3 for
p=1/16 and
s={1,2,5,10}.
0 10 20 30 40 50
k
0.00
0.01
0.02
0.03
0.04
0.05
0.06
0.07
p
Figure 3: The probability
)1(
)1(
k
coll
p
÷
according to (10) for
p=1/16 and s={1,2,5,10}.
As seen in Fig. 3, each curve approaches a
horizontal asymptote with growing number of
transmission attempt k. These asymptotes
corresponding to the limits:
)1(
)1(
)1(
lim
k
coll
k
coll
pp
÷
∞→
=
(11)
for various
s and denoted by
)1(coll
p defines the
probability of collision in any attempt in a given
transmission cycle.
By setting (10) to (11):
(
)
(
)
()
1
)1(
11
11
+
−−
−−⋅
=
s
s
coll
p
pp
p
(12)
As follows from (12), the
)1(coll
p depends both
on the
p value and the number of contending stations
s. The plots of
)1(coll
p versus the persistence level p
for various numbers of contending stations
s is
presented in Fig. 4.
As seen in Fig. 4, the probability
)1(coll
p grows
with increasing
p but it is at the same time smaller
than
p for any number of contending stations s.
This conclusion may be also derived analytically on
the basis of (12) as follows:
(
)
(
)
()
p
p
pp
p
s
s
coll
<
−−
−−⋅
=
+1
)1(
11
11
(13)
because
(
)
()
1
11
11
1
<
−−
−−
+s
s
p
p
for s≥1, and furthermore:
()
(
)
()
p
p
pp
p
s
s
s
coll
s
=
−−
−−⋅
=
+
∞→∞→
1
)1(
11
11
limlim
(14)
Thus, the probability
)1(coll
p
of collision in any
attempt in a given transmission cycle is upper
bounded by the persistence level
p regardless of the
number of contending stations
s.
0. 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.
0.0
0.2
0.4
0.6
0.8
1.0
Figure 4: Plots of
)1(coll
p
vs. the persistence level p for
s={1,2,5,10}.
In Fig. 5, the plots of the
)1(coll
p
versus s for
p={1/4, 1/16, 1/64} are presented. Finally, in Fig. 6,
the
)1(coll
p versus s and p in 3-D plot are illustrated.
0 10 20 30 40 50
s
0.00
0.05
0.10
0.15
0.20
0.25
0.30
Figure 5: Plots of the
)1(coll
p versus s for p={1/4, 1/16,
1/64}.
s=2
s=1
s=10
p=1/64
p=1/16
p=1/4
s=1
s=5
s=10
)1(coll
p
)1(
)1(
k
coll
p
÷
s=2
s=5
EVALUATING MAXIMUM TRANSMISSION UNRELIABILITY IN PERSISTENT CSMA PROTOCOL
185

Figure 6: The 3-D plot of
)1(coll
p versus s and p.
By a comparison, the probability that a given
station participates in collision for non-persistent
CSMA with a number of
W contending slots equals
1/W and is independent of the number of contenders
(Koscielnik, Miskowicz, 2010).
4 CONCLUSIONS
We compare the maximum transmission
unreliability in the non-persistent CSMA and
persistent CSMA for the same average number of
contention slots in both schemes. In the persistent
CSMA, the latter equals simply 1/
p. In the non-
persistent CSMA, the contention window is constant
in each transmission cycle and equals
W slots.
As proved in (Koscielnik, Miskowicz, 2010), the
maximum probability of participating in a collision
in the non-persistent CSMA scheme is upper
bounded by 1/
W, that is, by the probability of a
selection of a single slot in the transmission attempt.
On the other hand, as follows from the present
paper, maximum probability of participating in a
collision by a given station, according to the
persistent CSMA scheme, is upper bounded by the
persistence level (
p), which a main parameter of the
protocol. Thus, the complementary results defined
by (14) are valid for the persistent CSMA scheme.
REFERENCES
Tay, Y. C., Jamieson, K., Balakrishnan, H., 2004.
“Collision-minimizing CSMA and its applications to
wireless sensor networks”, IEEE Journal on Selected
Areas in Communication, vol.22, pp.1048-1057.
Miśkowicz, M., Golański R., 2006. LON technology in
wireless sensor networking applications, Sensors, vol.
6, no. 1, pp. 30-48.
Miśkowicz, M, 2009. Average channel utilization of
CSMA with geometric distribution under varying
workload, IEEE Transactions on Industrial
Informatics, vol. 6, no. 2, pp.123-131, 2009.
Egea-López, E., Vales-Alonso, J. Martínez-Sala, A. S.,
Bueno-Delgado, M. V., M. V. García-Haro, J., 2007.
Performance evaluation of non-persistent. CSMA as
anti-collision protocol for active RFID tags”, Lecture
Notes in Computer Science LNCS 4517, pp. 279-289.
Kleinrock, L., Tobagi, F.A, 1975. Carrier sense multiple-
access modes and their throughput-delay
characteristics, IEEE Transactions on Communication,
vol. COM-23, no. 12, pp. 1400-1416.
Lam, S.S., 1980. A carrier sense multiple access protocol
for local networks, Computer Networks, vol. 4, no. 1,
pp. 21-32.
Bruno, R., Conti, M., Gregori, E., 2002. Optimization of
efficiency and energy consumption in p-persistent
CSMA-based wireless LANs, IEEE Transactions on
Mobile Computing, vol. 1, no. 1, pp. 10-31.
Calì, F., Cont, M., Gregori, E., 2000. Dynamic tuning of
the IEEE 802.11 protocol to achieve a theoretical
throughput limit, IEEE/ACM Transactions on
Networking, vol. 8, no. 6, pp. 785-799.
Miśkowicz, M., 2009. Access delay in LonTalk MAC
protocol, Computer Standards & Interfaces, vol. 31,
no. 3, pp. 548-556.
Bianchi, G., 1998. IEEE 802.11—Saturation throughput
analysis, IEEE Communications Letters, vol. 2, no. 12,
pp. 318-320.
Miśkowicz, M., Kościelnik, D., 2010. On the upper bound
of transmission unreliability in memoryless backoff
contention, Proceedings of IEEE International
Workshop on Factory Communication Systems WFCS
2010, Nancy, France, May 2010.
p s
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
186
