FUZZY LOGIC BASED DYNAMIC PRICING SCHEME

FOR PROVISION OF QOS IN CELLULAR NETWORKS

Pamela Aloo, Djouani Karim, B. van Wyk and M. O. Odhiambo

French South Africa Technical Institute of Electronics, Tshwane University of Technology, Private Bag X680

Pretoria, 0001, Pretoria, South Africa

Keywords: Cellular networks, Fuzzy logic controller, Dynamic pricing, Quality of service (QoS), Network resources,

Network status information, Network set point, Revenue.

Abstract: Accurate forecasting of demand for cellular services is essential. The high infrastructure implementation

costs involved plus overestimation of demand can be very costly. In addition the difference between peak

and off-peak demands for wireless services can be very significant, both temporary and spatially. Gearing

the network to meet peak demand would result in under-utilised network capacity most of the time. It has

been suggested that real-time or dynamic pricing (variation of tariff according to network utilization) could

provide an additional strategy for encouraging more efficient use of available resources. The aim of this

research work is to investigate the implementation a Fuzzy Logic Controlled Dynamic Pricing (FLCDP) in a

simulated cellular network for improved quality of service (QoS). Improvement in revenue collection is also

investigated. Simulations were carried out using MATLAB. The results show that the network utilization is

improved and an increase in the system availability and reliability: which are the two major parameters for

QoS measurement. The revenue collected under FLCDP is greater than under flat rate pricing.

1 INTRODUCTION

The deployment of cellular networks is ever on the

increase and accompanying this increase is the user

demand for more services and the provision of

network QoS. The bandwidth and frequency

spectrum for mobile services is critically limited,

leaving very little room within which to manoeuvre

to provide the demand for more network services

and to meet network QoS requirements. To address

these limitations, the cellular network service

providers need new tools to efficiently and

effectively optimize their networks Abiri 2001 and

to support QoS schemes in the networks. A number

of solutions have been proposed based on cell

splitting and frequency re-use Bouroche 2003,

dynamic channel allocation or alternative routing

Ahmad 1999, and adaptive cell-sizing algorithm.

These methods often imply either an increase in

system complexity/deployment or a significant

degradation of the QoS. The alternative approaches

proposed in the literature, Ahmad 1999, Peha 2000,

Fitkov-Norris 2000, Hou 2001, Viterbo 2001 and

Yaipairoj 2004 are based on dynamic pricing

strategy to modify the user demands to fit within the

available network resources and thereby provide

network QoS.

1.1 Dynamic Pricing Strategy

Currently implemented network services pricing

schemes are static, either depending on the time of

the day or on defined ON and OFF peak periods.

However, a major drawback of the current pricing

schemes is their inflexibility and inability to account

for network load and status of the network resources

to vary the price according to the demand for the

network resources. Dynamic pricing strategy aims to

set the price for network services as a function status

of the network resources. For example, when

congestion is experienced in the network due to high

demand of network resources, the price goes up and

goes down when the demand is low. The price

information is made available to the users to decide

on whether to pay the current price for the network

services. The users are required to value their

communication and to decide whether to pay the

high price or wait until the price decreases to a value

they are willing to pay. The overall effect is a

decrease in the number of users, resulting in less

Aloo P., Karim D., van Wyk B. and O. Odhiambo M. (2010).

FUZZY LOGIC BASED DYNAMIC PRICING SCHEME FOR PROVISION OF QOS IN CELLULAR NETWORKS.

In Proceedings of the International Conference on Wireless Information Networks and Systems, pages 67-74

DOI: 10.5220/0002961400670074

 SciTePress

demand for network resources and a reduction in

congestion being experienced in the network. During

low demand for the network resources, the price is

reduced to allow more users into the network. Thus,

dynamic pricing strategy adjusts the price for the

network services taking into account the status of the

network resources.

Dynamic pricing has been mainly used to control

wired networks supporting Internet-based services

Paschalidis 2003, Peha 2000. Techniques for

deriving the optimal rates have been proposed,

which charge user on the basis of the congestion

they cause to the network. Dynamic pricing on

cellular networks is a resent research domain. In

Fitkov-Norris 2000 a self –regulated system is

proposed and the goal of the algorithm is to

maximize both the revenue for service provider and

the welfare of the users, that is, to choose the pricing

function, which offers the best utilization of system

capacity whilst keeping the call blocking probability

at a desired level. A new dynamic pricing scheme

for cellular networks is proposed in Hou 2001.

Unlike Fitkov-Norris 2000, Hou 2001 and Hou 2002

introduces the notion of incorporating dynamic

pricing and call admission control. In Viterbo 2001

yet another approach to dynamic pricing in mobile

networks is presented which is based only on

connection oriented services. Another interesting

paper is Yaipairoj 2004, gives mobile users

alternatives by either accepting the services with

higher price based on dynamic pricing scheme or

holding on to the conventional scheme (fixed low

rate) with acceptable degradation in performance.

In this paper, we propose dynamic pricing strategy

for network services which is controlled by a fuzzy

logic system. The price charged for the network

services varies with the network load or the status of

the network resources. The main objectives are to

implement a fuzzy logic based dynamic pricing of

the network services. Control theories, especially

non-linear controllers, has found a wide range of

application in cellular networks. Call Admission

Control in cellular networks has been controlled

using fuzzy logic systems Doru 2004, Mino 2009,

Ravichandran 2009 or neural-fuzzy system

represented by Zhong 2008. Mobile location

estimation has also been implemented using fuzzy

logic controller like the work presented by Xuemin

2002. Ravichandran 2009 also introduces a system

in which fuzzy logic system can be used to allocate

bandwidth in a mobile multimedia network.

Therefore, dynamic pricing in cellular networks can

also be implemented using controllers. Hence, a

control-based dynamic pricing strategy in cellular

networks is proposed.

This paper is arranged as follows; section 1 provides

an overview of dynamic pricing strategy and the

road map of the paper. Section 2, describes the

operation of the dynamic pricing scheme, section 3,

presents the cellular system modelling. Section 4,

describes the controller design of the dynamic

pricing strategy, section 5 presents simulation test

results and the paper is concluded in section 6.

2 SYSTEM DESCRIPTION

The cellular network system is shown in Figure 1,

the status information of the network resources is

continuously gathered and is used to set the

price

(

)

kp for network services. The calls are

generated by the users A, B and C willing to pay

differentiated prices,

p ,

p , and

p respectively

for the integrated network services. The calls

generated pass through call admission control which

admits the calls into the cellular network when.

p ,

p or

p <

(

)

kp .

Figure 1: Dynamic pricing system components.

The total number of calls handled by the network is

given by:

),()(

handoffnew

fks

λλ

where

handoff

is handover calls from neighbouring

base stations,

)(ks is network throughput and

new

is calls admitted by the call admission control. The

network throughput )(

ks is maintained at a level to

ensure optimum utilization of the network resources.

d(k)

WINSYS 2010 - International Conference on Wireless Information Networks and Systems

This is achieved by dynamically varying the set

price and using the set price to control

new

The communication system incorporating dynamic

pricing strategy and revenue collection module

shown in Figure 1 is also used to collect the

cumulative revenue for integrated network services

over a fixed period when dynamic pricing strategy is

applied and when flat rate pricing strategy is applied.

3 CELLULAR SYSTEM TRAFFIC

MODELLING

In this section we mathematically model the

communication network traffic presented in Figure 1

A mobile network is a complex system and may not

be possible to produce a tractable model of such a

system. In this analysis a number of simplifications

are made to produce a model that captures essential

behaviour of the system. The main assumption made

is to ignore all call hand-offs, that is

handoff

assumed to be zero. This is a significant

simplification as hand-off calls make up

approximately two thirds of the traffic in the used by

Hou 2002. However there is no universally agreed

hand-off call model because they depend on various

parameters (new call entrance rate, hand-off call

probability, cell dwell time, call duration) thus,

including hand-off calls makes the model

significantly more complex. The network throughput

is denoted by )(

ks , whose unit is the maximum

number of packets that can be transmitted over the

link per unit time.

According to (Bin 2003), the arrival of new

voice calls for guaranteed services and new data

calls for best-effort services are Poisson distributed

with arrival rate

()

and

()

respectively.

Hence, the total arrival rate is

() ()

(

)

kkk

λλλ

=+ .

In a dynamic priced network, the total arrival rate

does not only depend on the time but also on the

price for the network service charged at any time

k .

In the modelling of the mean arrival rate of the

telecommunication system,

()

is a function of

nominal network load, network demand and price.

The mean arrival rate is also such that it is zero

when there is no demand. This model resulted in;

() () ()()()(){}

030201

DkdkpPNkdk −+−+=

(1)

where,

321

κκκ

are constants,

()

kd is the dynamic

demand (in percentage),

D is the nominal demand,

P is the nominal price,

N is the nominal network

load, and

(

)

kp dynamic price.

The number of arrivals in time

k is Poisson

distributed with probability distribution given by

{}

(

)

(

)

(

)

{

}

.Pr

ekkdkp

ncallofNo

−

()

..0,1,2.n =

(2)

where, Pr is the probability function,

()

(

)()

kkdkp ,,

is the system call arrival rate,

k is time and n is the

number of calls.

Call duration was modelled by exponentially

distribution represented in equation 3 with a

specified departure rate

k .

{

}

0 .Pr

ecallofNo

−

(3)

The acceptance of packets is also follows Poisson

distribution.

In general, the arrival and traffic modelled by

equations (1), (2) and (3) are presented in Figure 2.



Figure 2: A simple telecommunication network traffic

model.

4 CONTROLLER DESIGN

The system utilization (Figure 3) shows that the

number of calls in progress/network loads, ranges

from 15% to 99% under flat rate pricing. This

indicates that the network services are not optimally

utilized at all times of the day. In dynamic pricing

strategy, we desire that the deviation between the

network utilization level and the network optimal

level is minimal at all times. In the controller design,

we choose a point at which the network service

provider wishes to operate (network optimal level).

At the chosen point, the network service provider

guarantees users satisfaction and the revenue

collection results in profit for the service provider.

To determine the optimum point for network usage,

set points or optimal points from 3000 to 7000 units

were investigated.

FUZZY LOGIC BASED DYNAMIC PRICING SCHEME FOR PROVISION OF QOS IN CELLULAR NETWORKS

Figure 3: Simulated traffic pattern for flat rate pricing.

The following steps were followed in designing the

system:

Choose a reference point for the network

operator.

Determine the parameters for system

training, inputs and outputs.

Training of the Fuzzy Logic system with

the price as the output and error in network

load and change of this error as the input.

Apply the trained system to dynamically

regulate the price depending on the network

load.

Three reference points, namely 3000 (40%), 5000

(62%) and 7000 (88%), were chosen. In control

theory, for a single input system, there are two

inputs to the fuzzy logic system; error (command-

feedback) and the error-dot (rate of change in error).

For this system, the error represents the difference in

reference point and the system throughput, while the

error-dot represents the rate of change of this error at

any given time. The outputs of each of the fuzzy

logic are then used to test the modelled cellular

network as represented in Figure 5.23. The system

throughput is then feedback for control purposes.

Each network throughput is fed back to be compared

with the reference point and for further control.

Figure 4: Fuzzy logic-base dynamic pricing.

The modelled fuzzy controlled dynamic pricing

scheme shown in Figure 4. The operation of the

proposed scheme is divided into two major sections:

• Training section

• Testing section

The training section involves fuzzification of the two

inputs, determination of membership functions and

the fuzzy inference rules. The following steps were

followed in training the system:

The fuzzy parameters of error and error-dot

were described by the following adjectives:

“negative”, “zero” and “positive”. To represent

these linguistic variables the following notations

were used:

For error, the following are defined:

Negative Error Ne, Zero Error Ze and, Positive

Error Pe. For error-dot, the following are

defined Negative Error-dot Nd, Zero Error-dot,

Zd and Positive Error-dot Pd.

The output of the system is the service price

whose linguistic variables were denoted by

Negative Price offset Np, Zero Price offset Zp

and Positive Price offset Pp.

Determination of the membership functions: To

obtain the membership functions, the example

given by Kosko 1997 was followed, where both

triangles and trapeziums are used to construct

the membership function because they are

suitable for real-time operation Zadeh 1994. For

set point 3000 units, the membership functions

of each of the inputs and outputs are given in

Figures 5, 6, and 7. The other set points, 5000

and 7000 units had a similar membership

function except for the range in the x-axis.

Figure 5: Error membership functions.

WINSYS 2010 - International Conference on Wireless Information Networks and Systems

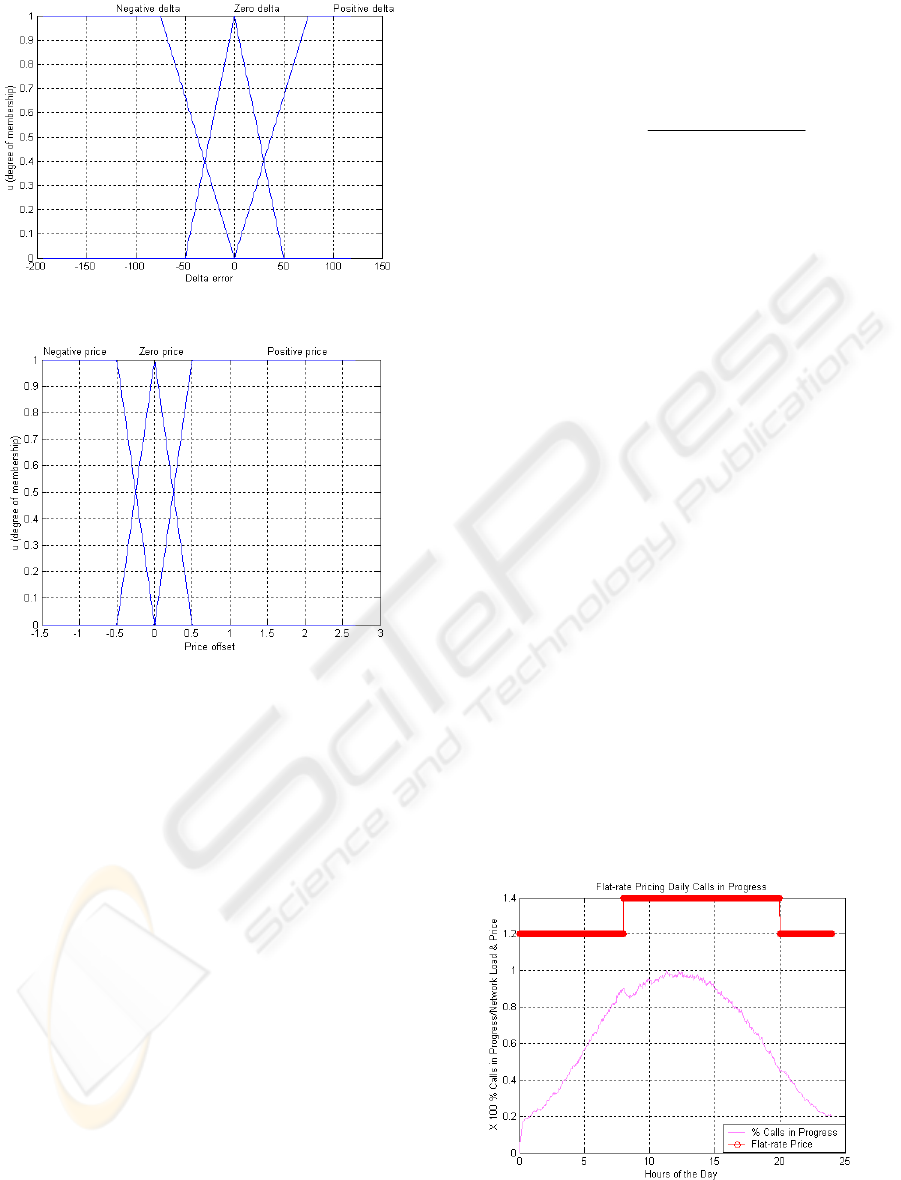
Figure 6: Error-dot membership functions.

Figure 7: Price offset membership functions.

3. Nine sets of Mamdami type Fuzzy Inference

Mamdani 1974 rules are derived for each

reference point and every rule presents a fuzzy

relation between the inputs (Error and Error-

dot) and the output (price) as follows;

If Error = Ne AND Error-dot=Nd, THEN the

Priceoffset =Np

If Error = Ze AND Error-dot=Nd, THEN the

Priceoffset =Pp

If Error = Pe AND Error-dot=Nd, THEN the

Priceoffset =Pp

If Error = Ne AND Error-dot=Zd, THEN the

Priceoffset =Np

If Error = Ze AND Error-dot=Zd, THEN the

Priceoffset =Zp

If Error = Pe AND Error-dot=Zd, THEN the

Priceoffset =Pp

If Error = Ne AND Error-dot=Pd, THEN the

Priceoffset =Np

If Error = Ze AND Error-dot=Pd, THEN the

Priceoffset =Np

If Error = Pe AND Error-dot=Pd, THEN the

Priceoffset =Pp

4. Deffuzification of each of the fuzzy outputs was

obtained using the CoG method represented in

equation 4.

() () ()

()

∑

−

,min

321

dotErrorError

PdotErrorError

nnn

kpkpkp

(4)

where

(

)

is the price for each set point,

()

dotErrorError −,min

is the combined

membership value for the two inputs and

the centroid for the price membership.

5 SIMULATION TEST RESULTS

In this section, we present the results obtained using

our analytical model simulated in MATLAB. We

ran two simulation tests: the first test (section 5.1)

was to investigate how to optimize the usage of the

network resources under dynamic pricing and flat

pricing schemes. The second test (section 5.2) was

to collect the total revenue over a fixed time period

when both dynamic pricing and flat pricing schemes

are applied and to compare the revenue collected.

5.1 Network Resources Utilization

The calls arrival pattern under flat rate pricing

strategy is shown in Figure 8. It can be observed that

the utilization of the network is not uniform. At

certain times the network is under /over utilized. The

network service provider increases the price during

peak time and reduces during off-peak.

Figure 8: Network Load and Price under Flat Rate Pricing

Scheme.

FUZZY LOGIC BASED DYNAMIC PRICING SCHEME FOR PROVISION OF QOS IN CELLULAR NETWORKS

The simulated cellular network under dynamic rate

pricing strategy shown in Figure 9 indicate that in

the FLCDP system, the network utilization is

improved by the reduction in the call arrival rate at

overload and reduction of call arrival rate at under

load. The reduction at overload decreases with

increase in network set point while increment at

under-load increases with increase in the network set

point.

Figure 9: Network Utilization under Dynamic Pricing

Scheme.

Figure 10 show that the dynamic price charged for

the services depends on the network load shown on

Figure 9. The simulation results (Figure 9 and 10)

can be used to argue that dynamic pricing can be

used to influence the user demand for the services

and, the demand influences the availability of the

network resources and hence pricing.

Figure 10: Price Charged under Dynamic Pricing Scheme.

The high price discourages the user from utilizing

the network services, freeing the network resources

thus, resulting in high network availability. The low

the price encourages the user to utilize the network

services by admitting more users into the network

resulting in high demand for the network resources.

Whenever there is an imbalance between the

availability of the network resources and the demand

for the network services, dynamic pricing can be

used to maintain the availability of the network

resources at an optimum level as shown in Figure 9.

5.2 Total Revenue Collected for the

Network Services

Based on the cellular network system shown in

Figure 1, we ran simulation test to collect the total

revenue under flat-rate and dynamic pricing schemes

for a period of 24 hours. The results obtained are

shown in Figure 11. Investigation of the revenue

collected was not the objective of the research but an

offshoot of the research to find out if there would be

any difference in revenue collected under dynamic

and flat rate pricing schemes. The revenue collected

under FLCDP is greater than that of flat rate pricing

and the difference increases with decrease in

network set point. The difference in collected

revenue for the different set points is due to the fact

that at low set point, many users could be willing to

pay the set price. While at high set point, very few

users could be willing to pay the high set price.

The high revenue collected under dynamic pricing is

because Dynamic Pricing Scheme maintains optimal

utilization of the network resources thus resulting in

more users and more revenue collection. While

under flat rate pricing scheme, users are discouraged

when the price is high, resulting in non-optimal

utilization of network resources and hence low

revenue.

Under the dynamic pricing scheme, new users

willing to pay the current services price are always

being admitted into the network, contrary to the flat

rate pricing scheme which blocks users when the

network resources are consumed. The resulting

cumulative revenue collected is thus higher under

dynamic pricing scheme as compared to flat rate

pricing scheme.

WINSYS 2010 - International Conference on Wireless Information Networks and Systems

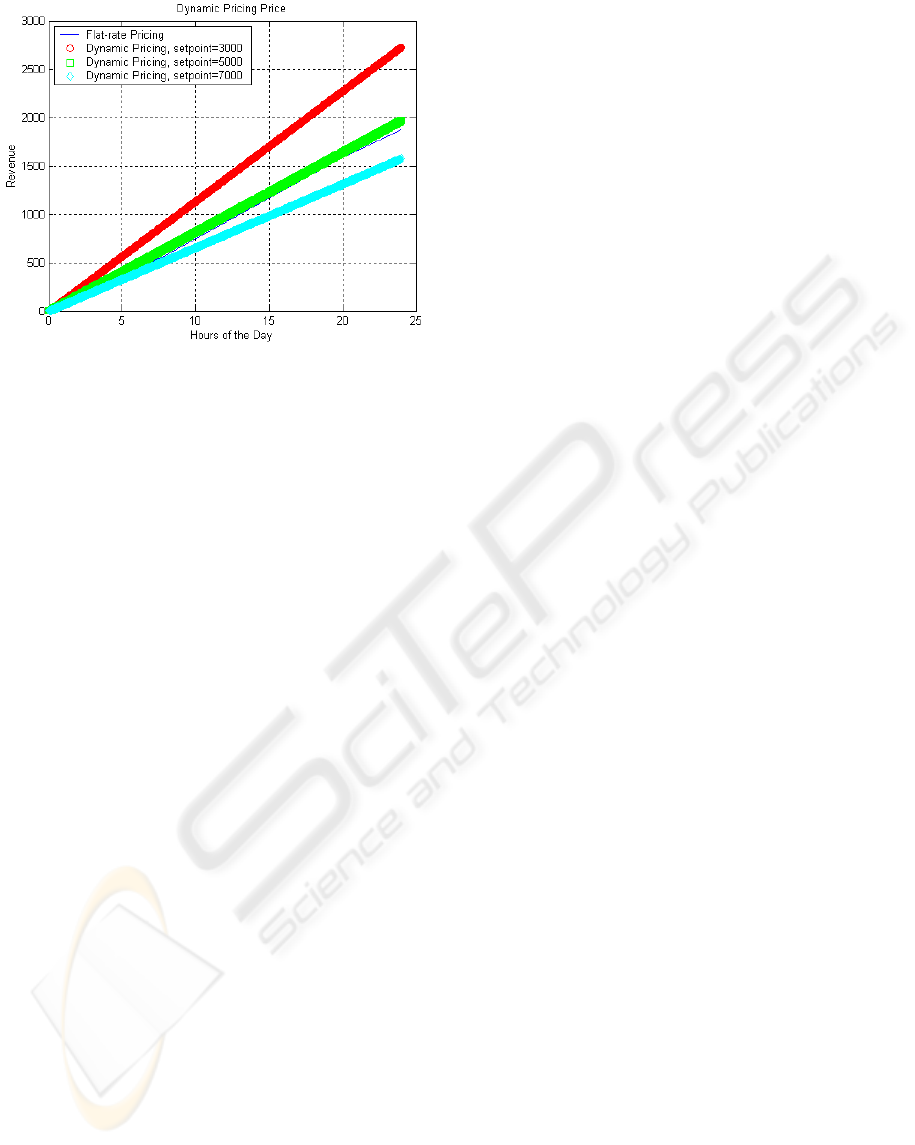
Figure 11: Revenue under Flat-rate and Dynamic Pricing.

Under the dynamic pricing scheme, new users are

always being admitted into the network as opposed

to the flat rate scheme thus, the resulting cumulative

revenue collected is higher in dynamic pricing

scheme as compared to flat rate scheme.

6 CONCLUSIONS AND FUTURE

WORK

The simulation results in Figure 9 show that an

optimal usage of the network resources is achieved

under dynamic pricing as compared to flat rate

pricing scheme. Regulating the price charged for the

network services under dynamic pricing scheme as

indicated in Figure 10, provides a mechanism to

maintain the status of the network resources at an

optimum level. In the flat rate pricing, when

congestion (due to scarcity of network resources) is

experienced in the network, new calls are blocked or

dropped resulting in high blocking probability.

While in the dynamic pricing scheme, when

congestion is experienced, the network service price

is increased thus only the users willing to pay the

new network service price will use the network. This

results in a lower blocking probability or fewer

dropped calls. By dynamically varying the network

price, the service provider provides the network

services to at a price the users are willing to pay.

The resulting better usage of the network resource

and the fewer blocked/dropped calls enables the

service provider to guarantee the quality of service

to the user, as the system ensures system availability

and reliability. The results obtained in this research

have shown that the fuzzy-based dynamic pricing

scheme can be used by the network service provider

as a mechanism to support network QoS to the users.

When the results in Figure 11 for dynamic and flat

rate pricing schemes is compared, it is observed that

total cumulative revenue collected is higher under

dynamic pricing scheme. The conclusion drawn

from these results is that implementing dynamic

scheme would result in more revenue for the

network service providers if the service provider

chooses the optimal operating point appropriately.

Dynamic pricing strategy converts congestion,

delays and queue costs into monetary values for the

service provider.

Future work includes considering that each network

service has a unique traffic and how this type of

dynamic pricing scheme can be implemented in the

real network.

REFERENCES

L. A. Zadeh, “Fuzzy Logic, Neural Networks, and Soft

Computing”, Communication of ACM, Vol. 37, No.3,

pages 77-84, March 1994.

R. Abiri, “Optimizing service Quality in GSM/GPRS

Networks,” In Focus, September 2001.

M. Bouroche, “Meeting QoS Requirements in Dynamic

Priced Commercial Cellular Network,” Masters

Thesis, University of Dublin, September 2003.

K. Ahmad, E. Fitkov-Norris, “Evaluation of Dynamic

Pricing in Mobile Communication Systems,”

University College London, 1999.

Q. Wang, J. M. Peha, M. A. Sirbu, “Optimal Pricing for

Integrated-Services Networks with Guaranteed Quality

of Service,” Carnegie Mellon University, Chapters in

Internet Economics, MIT Press, 1996.

I. C. Paschalidis, J. N. Tsitsiklis, “Congestion-dependent

Pricing of Network Services,” IEEE/ACM

Transactions on Networking, vol.8, No.2, pp.171-84,

April 2003.

J. M. Peha, “Dynamic Pricing and Congestion Control for

Best –Effort ATM services,” Computer Networks,

Vol.32, pp. 333-345, March 2000.

E. D Fitkov-Norris, A. Khanifar, “Dynamic Pricing In

Mobile Communication Systems,” In First

International Conference on 3G Mobile

communication Technologies, pp 416-420, 2000.

J. Hou, J. Yang, P. Symeon, “Integration of pricing and

call admission for wireless networks,” In IEEE 54

Vehicular Technology Conference, Vol. 3, pp 1344-

1348, 2001.

E. Viterbo, C. F. Chiasserini, “Dynamic Pricing for

Connection Oriented Services in Wireless Networks,”

In 12

IEEE International Symposium on Personal,

Indoor and Mobile Radio Communications, Vol.1, pp.

A-68-72, September 2001.

FUZZY LOGIC BASED DYNAMIC PRICING SCHEME FOR PROVISION OF QOS IN CELLULAR NETWORKS

Bin, L., Lizhong, L., Bo, L., & Xi-Ren, C., “On handoff

performance for an integrated voice/data cellular

system.” In Wireless Networks, vol.9:393-402,2003

Kosko B., “Fuzzy Engineering”, University of Southern

California, Prentice Hall, Upper Saddle River, New

Jersey, 1997.

Mamdani, E. H. & Assilian, N. S., “A Case Study on the

Application of Fuzzy Set Theory to Automatic

Control.” In Proceedings in the IFAC Stochastic

Control Symposium, Budapest, 1974.

J. Hou, J. Yang, S. Papavassiliou, “Integration of Pricing

with Call Admission Control to Meet QoS

Requirements in Cellular Networks,” IEEE/ACM

Transactions on Parallel and Distributed Systems,

13:898-910, September 2002

Yaipairoj S. & Harmantzis F. C., “Dynamic Pricing with

Alternatives for Mobile Networks,” IEEE Wireless

Communications Networking Conference, 2004.

Doru T., Stefan H., Philip P., & John M., “Fuzzy-based

call admission control for GPRS/EGPRS networks,”

Transaction on Automobile control & Computer

Science, Vol. 49, 2004.

Mino G., Barolli L., Durresi A., Xhafa F., & Kayayama

A., “A fuzzy-based call admission control scheme for

wireless cellular networks considering priority of on-

going connections,” 29

IEEE International

conference on Distributed Computing System

workshop, 2009.

Xuemin S., Jon M. W., & Jun Y., “Mobile Location

Estimation in CDMA Cellular Networks by Using

Fuzzy Logic,” Wireless Personal Communications,

22:57-70, 2002.

Zhong Y., Kwak K. S. & Yuan D., “A novel cross layer

game knowledge sharing algorithm based on neural-

fuzzy connection admission for Cellular Awh Hoc

networking,” Computer Communications, Vol31,

pages 2946-2950, 2008.

Ravichandran M., Sengottavelan P., & Shanmugam D. A.,

“An Approach for Admission Control & Bandwidth

allocation in Mobile Multimedia Network Using

Fuzzy Logic,” International Journal of Recent Trends

in Engineering , Vol.1, May 2009.

WINSYS 2010 - International Conference on Wireless Information Networks and Systems