
Image Formalization via Descriptive Image Algebras
Igor Gurevich and Vera Yashina
The Institution of the Russian Academy of Sciences, “A. A. Dorodnicyn Computing
Center of the RAS”, 40, Vavilov str., Moscow, 119333, Russian Federation
Abstract. In the framework of the Descriptive approach to image analysis and
understanding, the concept of Image Formalization Space (IFS) is introduced.
The elements of IFS are the different image representation forms through which
a raw image passes while it is transformed into a recognizable form, i.e., into an
image model. The structure and the main objects of the IFS are characterized
and discussed. A system of concepts and a formal apparatus of descriptive
image models are introduced to state the main axioms constituting the
conceptual foundation for image formalization in image analysis and
recognition. The topology of IFS is given by descriptive image algebra defining
operations on pixels and their configurations, on pixel values, and on image
states constructed using these operations.
1 Introduction
A breakthrough challenge of theoretical computer science is to find automated ways
of processing, analyzing, evaluating, and understanding information represented in
the form of images. For developers of automated systems designed to handle images,
as well as for end users in automated or interactive modes, this automation is expected
to help to develop, adapt and check methods and algorithms for image recognition,
understanding, and evaluation: (1) choose optimal or suitable methods and algorithms
for image recognition, understanding and evaluation; (2) check the quality of initial
data and whether they can be used in solving the image recognition problem; (3)
apply standard algorithmic schemes for image recognition, understanding, evaluation,
and search.
To ensure automation, we need to develop and evolve a new approach to analyzing
and evaluating information represented in the form of images. For this purpose, the
Algebraic Approach of Yu.I. Zhuravlev [9] has been modified for the case when the
initial information is represented in the form of images. The result is the descriptive
approach to image analysis and understanding (DAIA) proposed and justified by I.B.
Gurevich [2] and developed by his students [3, 4].
By the middle of 1990s, it had become obvious that the following points are
critical to the development of image analysis and recognition: (1) understand the
nature of initial information - images, (2) find methods of image representation and
description that allow constructing image models designed for recognition problems,
(3) establish a mathematical language for a unified description of image models and
Gurevich I. and Yashina V. (2010).
Image Formalization via Descriptive Image Algebras.
In Proceedings of the Third International Workshop on Image Mining Theory and Applications, pages 19-28
DOI: 10.5220/0002961500190028
Copyright
c
SciTePress

their transformations that allow constructing image models and solving recognition
problems, (4) construct models to solve recognition problems in the form of standard
algorithmic schemes that allow, in the general case, moving from the initial image to
its model and from the model to the sought solution.
The DAIA gives a unified conceptual structure that helps develop and implement
these models and the mathematical language [2, 3, 4]. The main purpose of the DAIA
is to structure and standardize different methods, operations and representations used
in image recognition and analysis. The DAIA provides the conceptual and
mathematical basis for image mining, with its axiomatic and formal configurations
giving ways and tools for representing and describing the images to be analyzed and
evaluated.
In this work, we give a brief review of the main results concerning the system of
concepts characterizing the initial information - images - in recognition problems and
descriptive image models designed for recognition problems. The work consists of
three main sections (along with the Introduction and Conclusions). Section 1 deals
with the concepts needed to formally describe and represent images within the DAIA
as well as forms and mathematical objects that reproduce an image in the course of
constructing descriptive image models (DIM). We introduce the concept of Image
Formalization Space and define the basic states – aspects of image representations –
generated in the course of reducing images to a recognizable form (RF - recognizable
form). Section 2 formalizes the ways of characterizing images, transformations, and
objects needed to describe images in a form suitable for recognition algorithms.
Finally, we consider the scheme for DIM synthesis. The system of concepts and the
formal apparatus of DIM introduced form the necessary background to state the main
axioms of the mathematical theory of image analysis and recognition. Section 3 gives
a brief review of a new class of image algebras, viz. descriptive image algebras
(DIA), as the sought algebraic language to describe, compare and standardize image
analysis, processing and recognition algorithms. The topology of IFS is given by DIA.
With these algebras, we can combine and standardize procedures of processing image
models and their transformations.
2 Image Description Formalization
To develop methods of automating image recognition, we need to find efficient ways
to formalize images so as to reflect image semantics, information hidden in its
internal structure and the structure of the external bonds within the real world part
(scene) reproduced by the image. No systematic mathematical methods for image
formalization and analysis have been developed thus far. The overwhelming majority
of image handling methods are heuristic, and their advantages depend on the way they
use "non-depictive" tools to convey the "depictive" features of images.
In applied mathematics and computer science, constructing and applying
mathematical and simulation models of objects and procedures used to transform
them is a conventional method of standardization. It was largely the necessity to solve
complicated recognition problems and develop structural recognition methods and
specialized image languages that generated the interest in formal descriptions -
20

models of initial data -and formalization of descriptions of procedures for their
transformation in pattern recognition (and especially in image recognition in the
1960s) [1, 5, 6, 8].
The DAIA provides the conceptual and mathematical basis for image mining, with
its axiomatic and formal configurations giving methods and tools for representing and
describing the images to be analyzed and evaluated.
The system of concepts we introduced provides the basis for formal definition of
methods for synthesizing image models and descriptive image models designed for
image analysis and recognition problems. Defining the system of concepts, we take
into account the following properties of images: (1) An image consists of a collection
of points and a set of values associated with these points. (2) Manipulation of images
in image analysis involves operations on images and on different types of values and
quantities associated with these images. (3) An image is endowed with two types of
information, i.e., it is defined as spatial relationships between its points and some
types of numerical or other descriptive information associated with these points. (4) A
point set is a topological space. It consists of a collection of objects called points and
a topology which provides for the nearness of two points, the connectivity of a subset
of a point set, the neighborhood of a point, boundary points, curves, and arcs.
By its nature, the image is an object of complex information structure that
reproduces information on the initial scene, using the values of brightness of discrete
elements of the image, viz. pixels, patterns of image fragments, sets of pixels and
spatial and logical relations between patterns, sets of pixels and individual pixels.
What make images different from other tools for data representation is that they are
highly informative, visual, structured and natural in terms of human perception. An
image is a mix of initial (non-processed, "real") data, their realizations, and some
deformations. The realizations (as well as appropriate descriptions) reflect the
informational and physical nature of objects, events, and processes reproduced by the
image, while deformations are due to the technical characteristics of the tools used to
record, form, and transform the image in the course of constructing a hierarchy of
descriptions. Thus, when developing methods for formal description of images, in
addition to the brightness values of image pixels, we need to take into account the
extra information associated with it explicitly and implicitly.
To formalize an image description and its conceptual structure, it is natural to
assume that the initial image is given not only by its digital implementations but also
by context and semantic information that shows the ways of obtaining and forming
the image and/or some of its specific aspects.
The process of image model synthesis consists of a set of transformations applied
sequentially to a raw image. As a result, we have sequentially changing image
“states” corresponding to different degrees of formalization.
Thus, we can introduce the concept of Image Formalization Space (IFS).
Definition 1. The IFS is a set of image “states” (a raw image, image realization,
image representation, realization of image representation, image model [3]). The IFS
is a metric space, i.e., its elements are image states (phases of formal descriptions of
images). In this sense, the IFS is a phase space. The topology of this space is given by
some algebraic system, i.e. via some image algebra defining operations on pixels and
their configurations, on pixel values, and on image states constructed using these
operations.
21

To construct formalized image descriptions, transformations from the set of
transformations admissible for this type of images have to be applied to the entire
information available on the image. Thus, we need to study, first, the types of
information contained in the image (the space of initial data) and, second,
transformations that can be applied to initial images to reduce them to a form
supported by recognition algorithms (the space of transformations).
Descriptions of the ways of sequential and/or parallel application of
transformations from the space of transformations to the initial information from the
space of initial data constitute a set of schemes for constructing formal descriptions of
images (the space of image representations).
To be able to apply recognition algorithms to the obtained formal image
descriptions, we need to implement the constructed schemes (implement image
representations), i.e., construct image models that result from reducing the initial
image (taking into account the entire information on the image) to a form supported
by recognition algorithms, i.e., to an RF. The space of image representations is an
intermediate space between the space of initial data and the space of image models.
Thus, the construction of image models involves synthesizing objects from the
following sets: (1) initial data - images; (2) image transformations that reduce images
to an RF; (3) image representations, viz. schemes for constructing formal image
descriptions; (4) realizations of image representations, viz. image representations with
chosen values of transformation parameters and structural elements included in a
representation; (5) image models.
3 Descriptive Image Models
To characterize images, the DAIA uses the following concepts: initial information (an
image together with its legend), its transformations, image representations,
realizations of image representations, and models. To define the types of states
undergone by the initial image in the course of constructing its descriptive model and
establishing the relations between these types, we introduce additional objects. These
are structuring elements, generating rules, semantic and context information on
images, digital representations of images, classes of image representations, classes of
image models, and the correct image model.
To define the main stages of image reduction to an RF, we consider some notions.
The DAIA assumes [4] that an image is described by a set of initial
information
0
{}
I
%
.
Lemma 1. The set of initial information
0
{}
I
%
consists of two sets {}
I
′
%
and {}B
%
: (1)
the set of realizations
{}II
′′
∈
%
of the image I that represent the given object or scene
such that
{( , ( ))}
f
x
D
Ixfx
∈
′
=
is the set of points x belonging to the domain of
definition
f
D
of the image realization
I
′
and the range of
()
f
x
at each point of
f
D
;
2) semantic and context information on the image
{}B
%
.
22
Definition 2 [4]. The Image Representation is a formal scheme designed to obtain a
standardized formal description of surfaces, point configurations, and shapes that
form the image and the relations between them.
Definition 3. The Image Model is a formal description constructed by applying a
realization of image representation to initial image representations.
Definition 4. The Realization of an Image Representation is an image realization
with chosen parameter values of the transformations involved in the representation.
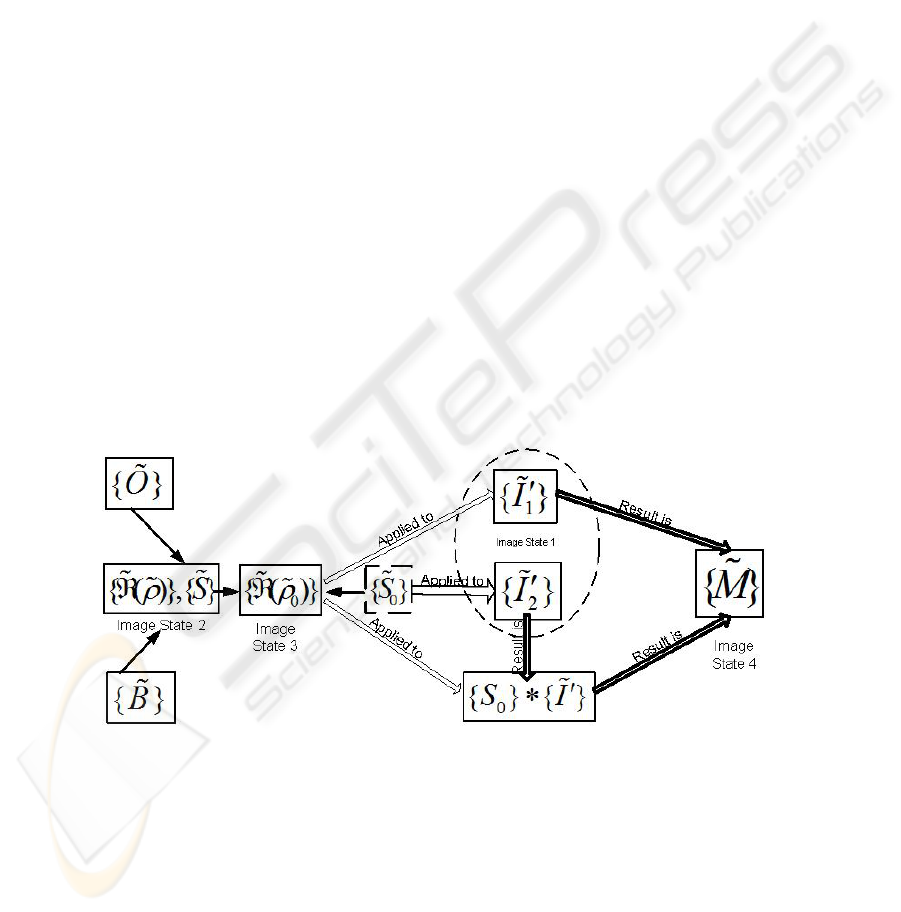
The synthesis of an image model is shown schematically in Fig. 1. The scheme for
DIM synthesis is based on the following principles: (1) the initial information consists
of the initial image realizations { }
I
′
%
(image state 1) and semantic and context
information
{}B
%
on the initial image; (2) an image representation {()}
ρ
ℜ
%
%
(image
state 2) is constructed by applying the transformations
{}O
%
chosen on the basis of
{}B
%
to initial image or a fragment of the initial image; (3) an image representation is
realized by choosing the transformation parameters
0
ρ
%
and structural elements
0
{}S
%
which help to process not only an image itself but also its fragments (the image
representation realization is
0
{( )}
ρ
ℜ
%
%
, which is image state 3); (4) an initial image
model { }
M
%
(image state 4) is constructed by applying
0
{( )}
ρ
ℜ
%
%
to the image
realizations
{}
I
′
%
or to image realizations after the structural elements have been
applied to them
0
{}*{}SI
′
%
%
(to the fragments of the initial image).
Fig. 1. Synthesis of a descriptive image model.
The DAIA deals with three classes of admissible image transformations, viz.
procedural, parametric, and generating transformations [3]. These classes generate
three classes of representations and three classes of image models. Three specialized
schemes for parametric, procedural, and generating image model synthesis were
constructed. The fundamental difference between these schemes and the general
scheme for image model synthesis lies in the corresponding transformations of image
realizations (parametric, procedural, and generating transformations) and in the use of
generating rules for synthesizing the generating DIM.
23

Proposition 1. Any T-model of the image I generates some realization of the image
I', i.e., the I-model of the image I.
Proposition 2. Any P-model of the image I generates some new semantic and context
information about the image
I.
Proposition 3. Any G-model of the image I generates some new semantic and context
information about the image
I.
The following axioms constitute the conceptual foundation for image formalization.
Axiom 1. Any image I can be unambiguously put into correspondence with the
totality of sets (
0
{}
I
%
, {}O
%
, { }
M
%
), where
0
{}
I
%
is the set of initial information, {}O
%
is
the set of transformations applicable to
0
{}
I
%
, and {}
M
%
is the set of results produced
by applying transformations to the initial information.
Axiom 2. The set of transformations {}O
%
of image states is given by the set of
structuring elements
{}S
%
, the set of generating rules {}R
%
and three subsets of
transformations: (1) procedural transformations
{}
T
O
%
, (2) parametric transformations
{}
P
O
%
, and (3) generating transformations
{}
G
O
%
.
Axiom 3. The Image Formalization Space (IFS) includes the Space of Initial Data
(image realizations), the Space of Realizations of Image Representations, and the
Space of Image Models. The IFS is a metric space with the following types of
elements: the states of an image (image aspects – image realizations and the phases of
its formalized descriptions), image representations, realizations of image
representations, and image models.
Axiom 4. The topology of the Image Formalization Space can be given via some
algebraic system – an image algebra, defining operations over image pixels, its
values, and image states constructed by applying the operations.
Axiom 5. The process of reducing an image to an easy-to-recognize form is totally
realized in the Image Formalization Space by Descriptive Image Algebras defined
over IFS elements – image transformations and image states.
4 Descriptive Image Algebras
As shown by the attempts made to create it, the formal apparatus to represent image
processing and analysis procedures in a uniform and compact form should be based
on a formal system of image representation and transformation that meets the
following conditions:
− points, sets, models, transformations, and morphisms can be used as objects;
− each object is a hierarchic structure constructed of primitive objects by some
transformations;
24

− each transformation is a hierarchic structure constructed of basic transformations
by some transformations.
This formal system (which is essentially a formal language and formalisms based
on it) should allow:
− constructing formal configurations (for instance, algebraic structures) that make it
possible to apply methods from different branches of mathematics and computer
science in image processing, analysis and recognition;
− constructing accurate and compact image descriptions handy in terms of both the
way to interpret the actions performed and the development of new methods;
− describing transformations over images in the form of compact sets of simple
transformations both in the machine-independent form and in the form adapted to
particular architectures;
− creating specialized sub-languages to describe images and transformations over
them in certain classes of image recognition and evaluation problems;
− increasing the efficiency of software implementation;
− choosing the most efficient programming languages in terms of formal structures
that describe known algorithms of image processing, analysis and recognition.
Having analyzed the requirements to its functionality and mathematical
characteristics, we can see that the sought formal system should represent a certain,
special class of algebras that makes it possible to write any image transformation
algorithm as a combination of elementary basic operations. Thus, this class of
algebras should allow handling both main image models - analysis and recognition
objects - and main models of transformations that allow synthesizing and
implementing basic procedures of formal image description, processing, analysis and
recognition efficiently.
The DAIA defines a new class of image algebras, viz. DIA, as the sought algebraic
language to describe, compare and standardize image analysis, processing and
recognition algorithms. DIA makes the process of constructing and applying
algorithmic schemes of image mining flexible and standardized. To give problems,
objects and transformations associated with image mining, we use hierarchic
structures that result from applying DIA operations to the set of primitive problems,
primitive elements of the image and basic transformations. Within such approach, we
can vary methods of solving the sub-problem - use operations of image analysis as
DIA elements, keeping the overall image mining technique unchanged.
The sources of DIA development are investigations of 1970-1980’s in area of
pattern recognition and image analysis “algebraization”. An appearance and
investigations of new algebra follows directly from results of Yu.I.Zhuravlev
algorithm’s algebra [10] and studies on varied image algebras by S.Sternberg[9] and
G.Ritter[7].
Conducted investigation of publications centre around algebraic methods in image
analysis and recognition defines primary specific of new mathematic language: 1)
DIA were created for integration and standardization of procedures of image model
synthesis and their transformations; 2) DIA operands are image models (also initial
images themselves) and image transformations; 3) DIA operations are image analysis
and processing transformations; standard algebraic operations; algebraic closures,
linear combination and superposition of these operations; 4) algorithmic schemes for
25

formal image description, processing, analysis and recognition consist of elements
described by DIA and any used in scheme transformation is given by structures
constructed by applying DIA operations to a set of DIA operands; 5) to provide DIA
correspondence with requirements for mathematical object “algebra” restrictions on
basic DIA operations are introduced.
We recall the definitions of DIA (definition 5, 6).
Definition 5 [3]. An algebra is called a DIA if its operands are either image models
(both the image itself and the set of its related values and characteristics can be
chosen as a model) or operations over images or both.
Main DIA investigations were directed on study of DIA with one ring (DIA1K)
(definition 6), which is classical algebra of Van der Varden with non-classical
operands. To define DIA with several rings we propose to use a notion “graduated
algebra” and in case DIA with two rings a notion “superalgebra”. Further DIA
specific is defined by algebra properties.
Definition 6 [3]. The ring U, which is the finite-dimensional vector space over some
field P, is a
DIA with one ring if its operands are either image models or operations
over images.
What makes DIA special is that
− by imposing restrictions on basic DIA operations, new mathematical constructions
(DIA) ensure that we use the concept of algebra in its strict classical sense;
− basic DIA operations are introduced both over images and over arbitrary formal
representations of images as well as over image transformations.
The latter explains why this new type of algebras has the word "descriptive", viz.
dealing with image descriptions, in its name. Using the concept of «algebra» in its
strict classical sense in the DIA definition, we can single out basic DIA operations for
different types of operands, thus having the set of complete systems to describe image
analysis problems.
To construct algorithmic schemes for solution of image recognition problem we
should extract basic DIA1K classes, used for description of each scheme step. To
provide this fact we should introduce specialized DIA1K over initial and intermediate
information in image processing, analysis and recognition problems (DIA1K over
image models and over image realizations) and specialized DIA1K over
transformations of images and image models for generation of new image models.
On the basic of image model synthesis scheme (Fig. 1) there were extracted
specialized DIA1K classes for image model description and construction (Table 1).
Each DIA1K class generates rules for DIM construction by this DIA1K (theorems
and proposals were formulated and proved). Formulated theorems and proposals
define algebra property “to generate DIM”.
The Table 1 gives the basic DIA1K classes.
26
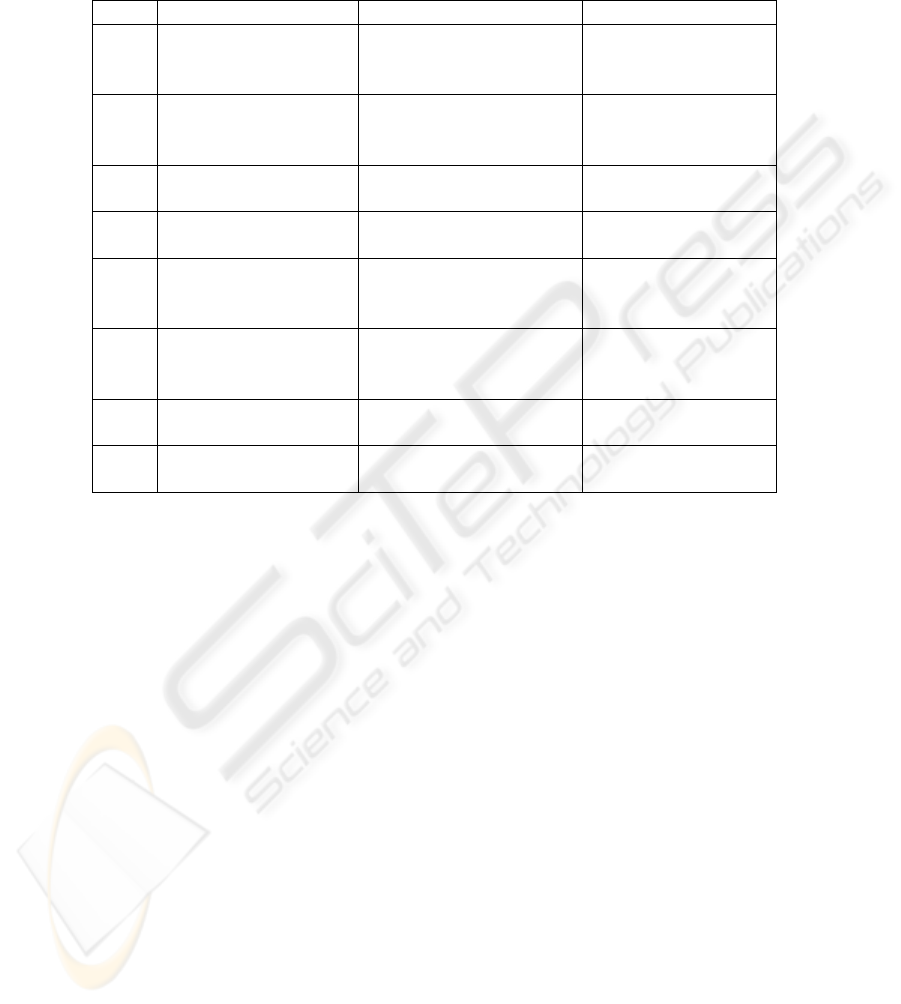
Table 1. Basic classes of DIA1K.
Class Algebra Operands Algebra Operations Algebra generates
1. Realizations of initial
images or realization
of image fragments
Procedural Image
Transformations
Procedural image
models, image
realizations
2.
Procedural image
transformations
Operations on procedural
transformations
Procedural image
models, image
realizations
3. Parametric image
transformations
Operations on parametric
transformations
Parametric image
models
4. Generating image
transformations
Operations on generating
transformations
Generating image
models
5.
Image Representations
Operations on image
representations
DIM; multi model
and multi aspect
image representations
6.
Procedural Image
Models
Operations on procedural
image models
Procedural image
models, image
realizations
7. Parametric Image
Models
Operations on parametric
image models
Parametric Image
Models
8. Generating Image
Models
Operations on generating
image models
Generating Image
Models
For more detailed information on DIA, see [3].
5 Conclusions
We introduce the concept of Image Formalization Space (IFS) as a set of image
“states” (a raw image, image realization, image representation, realization of image
representation, image model). The topology of this space is given by some algebraic
system, i.e. via some image algebra defining operations on pixels and their
configurations, on pixel values, and on image states constructed using these
operations.
Being developed as the fundamental basis for the mathematical theory of image
analysis and recognition, the DAIA allows introducing the axiomatics of the sought
theory. Five axioms were represented.
The DAIA defines a new class of image algebras, viz. DIA, as the sought
algebraic language to describe, compare and standardize image analysis, processing
and recognition algorithms. The topology of IFS is given by DIA. DIA makes the
process of constructing and applying algorithmic schemes of image mining flexible
and standardized. Main DIA investigations were directed on study of DIA with one
ring (DIA1K).
Basic DIA1K should satisfy following requirements: 1) to provide effective
representation of images and their models; 2) to provide representation of DIM [4] as
elements of information technology for image analysis, recognition and
understanding: а) to provide generation of basic DIM classes (P-, G-, T-, I- models);
27

б) to provide transformations of basic DIM classes; 3) to be elements of a basis of the
set of all DIA1K used for description image processing, analysis and recognition
problems; 4) to satisfy main propositions and conditions defined algebraic
constructions.
Eight classes of basic DIA were extracted.
Acknowledgements
This study was partially supported by the Russian Foundation for Basic Research
(grants no. 08-01-00469, 08-01-90022, 09-07-13595); the Mathematical Sciences
Division of the Russian Academy of Sciences ("Algorithmic Schemes for Descriptive
Image Analysis", project within the "Algebraic and Combinatorial Methods of
Mathematical Cybernetics and Information Systems of the New Generation" program
for fundamental research), and the Russian Academy of Sciences Presidium (project
no. 214 within the "Intellectual Information Technologies, Mathematical Modeling,
System Analysis and Automation" program for fundamental research No.2).
References
1. Grenander, U.: General Pattern Theory. A Mathematical Study of Regular Structure.
Clarendon Press. Oxford (1993)
2. Gurevich, I.B.: The Descriptive Approach to Image Analysis. Current State and Prospects.
In: Proceedings of 14th Scandinavian Conference on Image Analysis, LNCS 3540, pp. 214-
223. Springer-Verlag Berlin Heidelberg (2005)
3. Gurevich, I.B., Yashina, V.V.: Operations of Descriptive Image Algebras with One Ring.
In: Pattern Recognition and Image Analysis: Advances in Mathematical Theory and
Applications, vol.16, no.3, pp. 298-328. Pleiades Publishing, Inc. (2006)
4. Gurevich, I.B., Yashina, V.V.: Descriptive Approach to Image Analysis: Image Models. In:
Pattern Recognition and Image Analysis: Advances in Mathematical Theory and
Applications, vol. 18, no. 4, pp. 518-541. MAIK "Nauka/Interperiodica"/Pleiades
Publishing, Inc. (2008)
5. Marr, D.: Vision. Freeman. New York (1982)
6. Narasimhan, R.: Picture Languages. In: Picture Language Machines(ed. S.Kaneff), pp. 1-
30. Academic Press, London, New York (1970)
7. Ritter, G.X., Wilson, J.N.: Handbook of Computer Vision Algorithms in Image Algebra. 2-
d Edition. CRC Press Inc. (2001)
8. Rosenfeld, A.: Picture Languages. Formal Models for Picture Recognition. In: Academic
Press. New York, San Francisco, London (1979)
9. Sternberg, S. R.: An overview of Image Algebra and Related Architectures. In: Integrated
Technology for parallel Image Processing (S. Levialdi, ed.). London, Academic Press
(1985)
10. Zhuravlev, Yu.I.: An Algebraic Approach to Recognition and Classification Problems. In:
Pattern Recognition and Image Analysis: Advances in Mathematical Theory and
Applications, vol.8, pp.59-100. MAIK "Nauka/Interperiodica" (1998)
28
