On the Construction of Gestalt-Algebra Instances and a

Measure for their Similarity

Eckart Michaelsen

Fraunhofer IOSB, Gutleuthausstrasse 1, 76275 Ettlingen, Germany

Abstract. Four construction principles that compose more complicated percep-

tual gestalts from less complex ones are defined in detail: Mirror gestalts, lat-

tice gestalts, rotational mandalas, and clusters, respectively. These can be en-

capsulated as constructions in a production system. Since any of the four con-

structions can work on any gestalt, a recursive and very expressive scheme is

set up with many prospective applications in image mining. Of particular inter-

est is such analysis for aerial and satellite images and for façade images of

buildings.

1 Introduction

Gestalt is ubiquitous in nature as well as in man-made artifacts. Recognition of gestalt

goes far beyond today’s understanding of “pattern recognition”. We have to drop

back to a naïve understanding of the word “pattern”, to forget the feature vectors we

are used to deal with in the pattern recognition community and imagine patterns we

perceived occasionally in a more contemplative situation. Usually we are not aware of

the mathematics, particularly of the implicit algebra in our intuitive understanding of

gestalt, like symmetries, repetition, rotational mandalas, variation, etc. Understanding

the word “recognition” according to its Latin roots means to reconstruct the hidden

gestalt idea, resulting, as far as possible, in the most probable explanation. The

appearance of a gestalt is uncertain – there may be displacement, deletion and clutter.

Humans still recognize the gestalt. For a machine, however, this poses a very hard

search task which nonetheless is indispensible for real content-based image mining.

1.1 Related Work

For more than thirty years now automatic analysis of complex aerial images has been

a challenge and also basic approaches to their algebraic gestalt have been attempted

[11]. Today emphasis is more on learning of rules and stochastic modeling of con-

straints and relations [12]. Automatic understanding of buildings currently also in-

cludes façade analysis [17] including the grouping of semantically similar SIFT in-

stances in lattices [13]. The main economic motive is apparently application in the

games industry. The computer graphics community acknowledged that a deeper un-

derstanding of gestalt principles and design customs in architecture are prerequisite to

Michaelsen E. (2010).

On the Construction of Gestalt-Algebra Instances and a Measure for their Similarity.

In Proceedings of the Third International Workshop on Image Mining Theory and Applications, pages 51-59

DOI: 10.5220/0002962400510059

 SciTePress

swift setup and detailed elaboration of cyber city models [16]. This includes work for

archeologists as well. Up to now we are not aware of much other work on gestalt

recognition in our understanding in the machine vision community. This paper con-

tinues work presented in [8, 10]. Here we focus on the precise construction methods.

2 Constructions of Gestalts

Given a set of points and corresponding assignments to orbits a new gestalt instance

is constructed by error sum minimization. The errors are displacements between the

actual positions of the points and the set positions given by the gestalt principle and

the corresponding attribute values. All gestalts are given modulo the action of a par-

ticular group on the indices of the points, which do not alter the identity of an in-

stance. We distinguish the following constructions:

2.1 Mirror Symmetry Gestalt

Given k pairs (p

1,0

, p

1,1

), …, (p

k,0

k,1

) of points in the usual 2D vector space, we are

looking for an optimal axis a such that by a mirror mapping according to this axis the

points p

i,j

are flipped into the points p

i,j+1

in the least squares error manner. Here we

have i=1…k, and j=0,1 to be understood modulo 2. We can decompose the constraint

into two parts: 1) The axis should be incident with the k midpoints (p

i,0

i,1

)/2. And

2) the axis should be perpendicular to the k difference vectors p

i,0

-p

i,1

. This leads to a

linear one-step solution using singular value decomposition of the matrix

1,01,1 1,01,1

,0 ,1 ,0 ,1

1, 0 1,1 1, 0 1,1

,0 ,1 ,0 ,1

xx yy

xxyy

kkkk

yy xx

yyxx

kkkk











 



 



pp pp

pppp

pp pp

pppp



(1)

(upper indices x and y indicate the coordinates in 2D). The eigenspace corresponding

to the least singular value is accepted as solution a (axis equation for the new gestalt).

Furthermore the new gestalt obtains the center of gravity of all points as position o.

We state here without proof that this algebraic solution approaches the desired least

squares solution – for which according to its non-linear setting an iterative calculation

would be necessary – provided that the coordinate system is chosen properly. For our

preference towards one-step linear algebraic solutions we refer to [4]. Figure 1 dis-

plays such minimization and the histogram of residuals. We have used particular such

gestalt instances in SAR-image understanding [9]. It is evident that this definition is

invariant under action of the trivial finite group of order 2 on the second index 0↔1.

The gestalt is understood modulo this group.

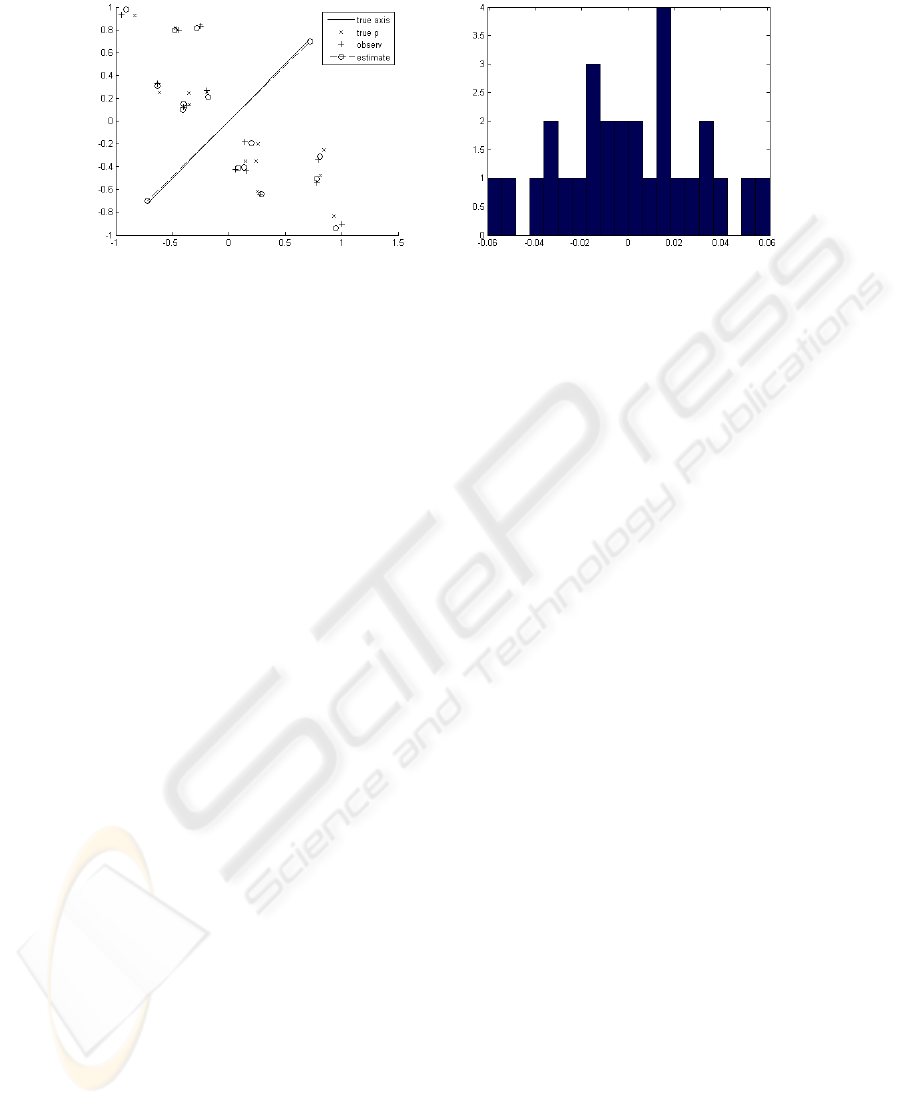
Fig. 1. Left: Construction of a mirror symmetry gestalt– here with k=7 point pairs and σ=0.07;

right: Histogram of the residuals.

2.2 Lattice Gestalt

Given k m-tuples (p

1,0

, …,p

1,m-1

), …, (p

k,0

, …, p

k,m-1

) of points, we are looking for an

optimal common start position p

and a shift vector v such that:

















()

io ij

jpvp

(2)

This is a linear problem and thus the one-step linear algebraic solution is indeed

the least squared error sum solution. It is just averaging the differences for v and

taking the center of gravity for o is optimal. The construction of the starting points

,i,o

is also trivial. A typical lattice gestalt is depicted below in Figure 3.

2.3 Rotational Gestalts

Given k m-tuples (p

1,0

, …,p

1,m-1

), …, (p

k,0

, …, p

k,m-1

) of points, we are looking for an

optimal common center point o such that by rotation with angle 2π/m the points p

i,j

are mapped onto the points p

i,j+1

in the least squares error manner. Here we have

i=1…k, j=0…m-1. This leads to a sum of squared errors reading

2/ , ,

()()

jkio ij









 





Mpopo

(3)

to minimized, where o and the vectors p

i,o

are varying. M

denotes the usual turning

matrix for angle α in 2D. Already from this definition can be seen that the gestalt has

to be understood modulo the finite rotation group of order m. I.e. a cyclic shift on the

indices j does not change the identity of the gestalt. The vector p

i,o

that results from

the minimization has to be understood as giving a radius for the ith orbit with its

length and a phase modulo 2π/m. Figure 2 shows the situation. Minimization of (3) is

a non-linear problem closely related to circle fitting.

We are not aware of a direct linear algebraic setting for it (such as is presented for

mirror gestalts above). We refer to the closely related circle fitting problem [6], and

initialize o by the center of gravity of all observed points and p

i,o

by p

i,0

. The itera-

tion is performed using the Jacobian displayed in (4). Entries to the matrix are the

partial derivatives ρ for the current iteration. As above the lower indices denote i (the

index inside the orbit), and j (the index of the orbit) respectively. Upper index x or y

denotes the direction in the plane. The parameter vectors p

i,o

are treated with radius r

and phase p. These are the other upper indices.











1,0 1,0

1, 1 1, 1

10 10

1, 1 1, 1

,0 ,0

,1 ,1







rx px

ry py

rx px

km km

ry py

km km

(4)

The columns of this matrix correspond to the parameters o

, o

, r

, p

, …, r

, p

and the rows to the current residuals. For iteration this matrix has to be squared and

inverted in each step. For the rotational gestalt we observed that convergence is

quick. Usually three or four steps are sufficient.

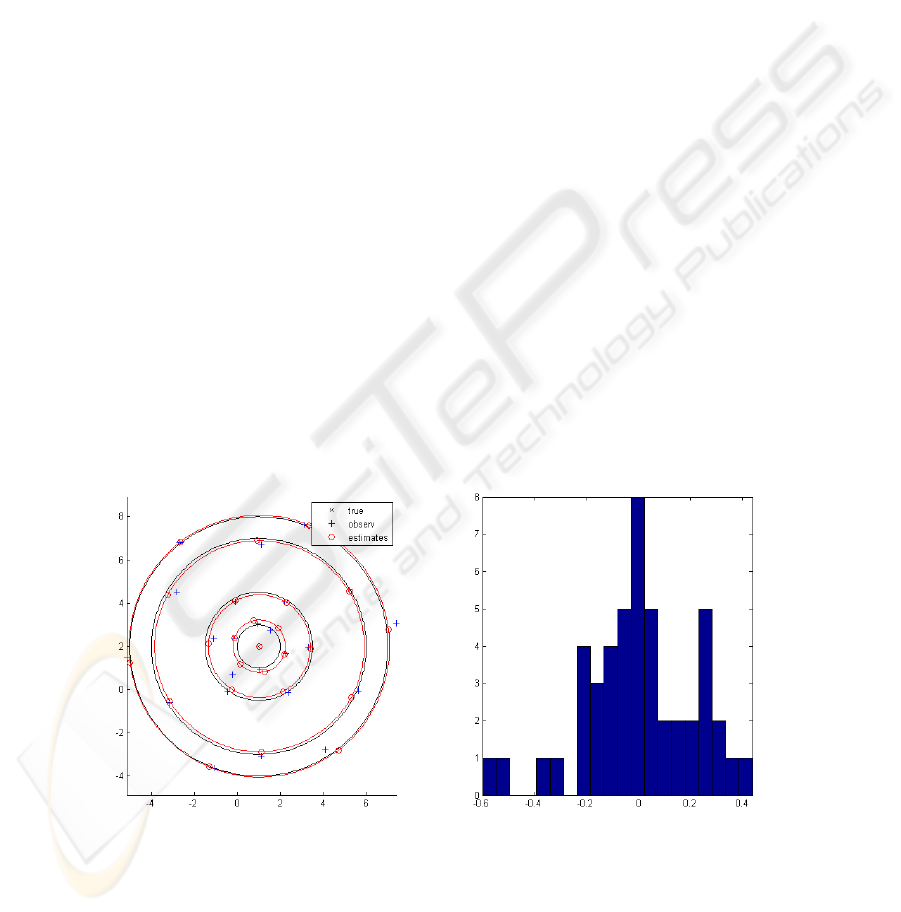
Fig. 2. Left: Construction of a rotational symmetry – here of order m=6 with k=4 orbits and

σ=0.25; right: Histogram of the residuals.

2.4 Cluster Gestalts

A very important principle in gestalt perception is proximity. This clusters a set of

adjacent points into a new gestalt by constructing the center of gravity as new posi-

tion o. Also the eigenspace corresponding to the larger eigenvector may be used as

orientation attribute v. Clustering also yields a sum of squared residuals. The parts are

added to the cluster gestalt as set – i.e. the full permutation group acting on the indic-

es of the parts does not alter identity of the cluster gestalt instance. Clusters are the

least significant gestalt. If any of the gestalt constructions listed above applies better,

they will be preferred.

3 Testing for Equality and Similarity

When entering a newly constructed gestalt instance into the database care has to be

taken that this gestalt has not yet been constructed in a different order or manner.

Actually, this is the part where algebraic knowledge is required most of all. In fact,

almost for any gestalt construction trees there are very many other possible construc-

tions. The same object may be described in different ways. Here we need canonic

representatives allowing swift tests for equality – and more important: A metric or

similarity measure that does not require extensive computational effort. For gestalts

with uncertainty care has to be taken, that all construction principles use the same

kind of residuals – here squared error sums – so as to compare two different descrip-

tions for the same set of primitives and decide for the simplest description with mi-

nimal squared error sum.

3.1 Sub-lattices and Lattices of Lattice Gestalts

Any lattice of size m can also be understood as lattice using -v as translation vector

and replacing j by m+1-j. Moreover, if m is not a prime number and thus can be de-

composed m=pq a lattice gestalt of order m can also be understood as lattice of size p

containing sub-lattices of size q (and vice versa). According to the Helmholtz prin-

ciple of the “maximal meaningful element” as claimed by A. Desolneux [3] the max-

imal gestalt is the preferred canonic description, in which the gestalt is to be stored in

the database. Particular lattice gestalts – of bright spots, i.e. salient scatterers - have

been investigated in [9] as well. This includes the preference for maximal gestalts

(scatterer rows).

Occasionally, we have coded a production system grouping rows of rows where

the outer gestalt has a different direction than the inner ones (preferably perpendicu-

lar) [15]. This can be seen as a practical step towards gestalt algebra. Columns of

objects which form again a row are one of the main examples, ubiquitous in facades

and remotely sensed industrial sites. Again, the situation is different with angle be-

tween the inner and the outer vector: Vectors of π/3, π/4 or π/6 difference in orienta-

tion and of equal length construct a 2D-lattice (triangular, orthogonal or hexagonal).

There is an elaborated theory on these wallpaper lattices [5] and also practical work

of recognition of such lattices [1]. We also refer to the investigations on 2D and 3D

lattices going on in Physics [14] and in particular in cristallography. In aerial images

or images of facades, in particular, orthogonal 2D lattices are not rare. However, we

do not introduce these as a special gestalt. Instead, the equality test has to take care of

the different possibilities. If the angle is not very close to one of the three wallpaper

possibilities, or if the length of the vectors v is different there will be a preferable

canonic representation: The classical gestalt principle proximity demands that the

closer objects are grouped first into the inner lattice, after that these columns are

grouped into rows – with longer distance vector v. Moreover, we are not treating

infinite lattices here.

3.2 Sub-rotations of Rotational Gestalts

In analogy to the lattice gestalts we have to take care here also whether m is a prime

number. If not it can be decomposed m=pq and the rotational gestalt can also be un-

derstood as rotational gestalt of order p or also q (in accordance to the decomposition

of the finite cyclic groups of order m). Again obeying the Helmholtz principle the

maximal gestalt is the preferred canonic description, in which the gestalt is to be

stored in the database, provided it yields no significantly larger error sum.

3.3 Equality of Lattice and Mirror Gestalts

It is easily verified that a lattice of symmetric gestalts can also be understood as mir-

ror symmetry provided that the symmetry axes of the parts a

are perpendicular to the

generating vector v. For an even m there will be k·m/2 mirror orbits created by flip-

ping i,j↔m-i,j and simultaneously switching the internal mirror indices. Figure 3

shows such a case. According to gestalt principles the simplest model is again pre-

ferred as canonic description – which is here of course the lattice.

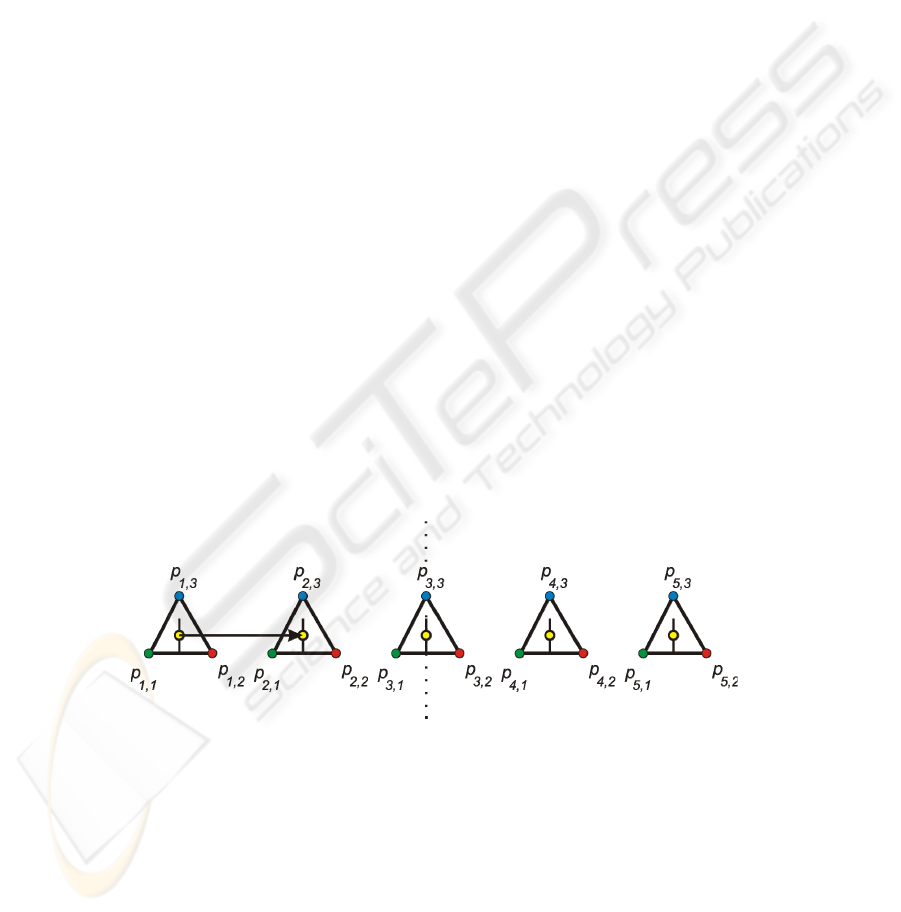
Fig. 3. A lattice with m=5 and k=4 orbits (traces); it can also be understood as mirror gestalt

with the axis displayed dotted.

3.4 Equality of Rotational and Mirror Gestalt

Provided that the axes of symmetric parts of a rotational gestalt all are incident with

the center of this rotational gestalt it can also be understood as a symmetry gestalt

with respect to any of axes of its parts. Here we have to change the rotation direction

of the indices in the orbits and also flip the internal mirror indices around. Rotational

symmetry is regarded as stronger than mirror symmetry. Thus such a gestalt will be

stored as rotation in the database, provided it yields no significantly larger error sum

4 Coding the Search for Gestalts as Production System

Searching for gestalt instances in measured image data using the algebraic structures

outlined above poses a non-trivial challenge. We recommend using the production

system interpreter as outlined e.g. in [9]. It has any-time performance, avoids com-

plete search, is quality driven bottom-up per default and allows sophisticated top-

down acceleration. The class Gestalt is inherited from the class CImageObject and

may thus be handled by this interpreter. All other classes listed in Table 1 below are

in turn inherited from the class Gestalt.

Table 1. Productions coding the gestalt constructions above.

Right side

comment construction Left side

MirrorGestalt ← only 2 instances Sect. 2.1 Gestalt, Gestalt

LatticeGestalt ← starting a row Sect. 2.2 Gestalt, Gestalt

LatticeGestalt ← continuing “ LatticeGestalt, Gestalt

RotatGestalt ← starting a row Sect. 2.3 Gestalt, Gestalt

RotatGestalt ← cont. until full “ RotatGestalt, Gestalt

ClusterGestalt ← Sect. 2.4 Gestalt, …, Gestalt

Productions for this interpreter usually have not only a construction function for

the right hand side but also a condition on the left hand side objects in order to avoid

any object to be combined with any other (constrained set grammar). This is omitted

here, because our approach attempts to construct a gestalt algebra – where indeed any

member should be a possible partner for any other member. In practice, however, a

threshold should be set on the residual error sum (which of course sets the quality

assessment driving the search). The constraint resulting from such a threshold can be

transformed into a search region setting a focus where to look for prospective partner

gestalts.

The productions listed in the table can construct arbitrarily complex gestalt alge-

bra instances such as sketched in [10]. First parts of this coding endeavor have al-

ready been accomplished. But there remain some questions which have to be ans-

wered before the whole system can be set up. These are discussed below.

5 Discussion and Conclusions

This contribution introduced in more detail the constructions necessary for setting up

gestalt algebra as indicated earlier in [8, 10]. It is our goal to add more precision and

detail on the way to the implementation of this structure for practical applications.

As long as the set of equality and similarity relations and canonical forms for ges-

talts, as listed in chapter 3, is not complete there is little sense in starting the coding

endeavor. While for infinite 2D lattices there is an elaborated mathematical theory at

hand for more than hundred years [2], we have no proof for completeness of the list

of Section 3 indicating possible different appearances of the same finite gestalt with

respect to all our gestalt constructions yet.

As indicated in Section 3 in the description of a composed gestalt simplicity in the

tree structure (flatness of hierarchy) has to be balanced against the achieved squared

residual sum. Another open problem concerns the scale: Gestalt instances with a deep

tree composed from many objects distributed on a large area should be assessed on a

different scale. But the common displacement error measure is a prerequisite of mu-

tual comparison for the gestalts. We are looking forward to interesting future work.

References

1. Agusti-Melchor, M., Valiente-Gonzalez, J.-M., Rodas-Jorda, A.: Lattice Extraction Based

on Symmetry Analysis. VISAPP 2008, INSTIC, Portugal, ISBN: 978-989-8111-21-0

(2008) 396-402

2. Bravais, A., "Mémoire sur les systèmes formés par les points distribués régulièrement sur

un plan ou dans l'espace", J. Ecole Polytech. Vol. 19 (1850) 1–128

3. Desolneux A., Moisan L., Morel J.-M.: From Gestalt Theory to Image Analysis. Springer,

Berlin (2008)

4. Hartley, R., Zisserman, A.: Multiple View Geometry. Cambridge Unv. Press, sec. edition

(2003)

5. Horne, C. E.: Geometric symmetry in patterns and tilings. Woodhead Publishing. Abington

Hall, England, ISBN 1 85573 492 3 (2000)

6. W. Gander, G. H. Golub, R. Strebel: Least Squares Fitting of Circles and Ellipses. BIT

Numerical Mathematics, Springer Netherlands, Volume 34, Number 4 / Dezember (1994)

7. van Leeuwen, J. (ed.): Computer Science Today. Recent Trends and Developments. Lec-

ture Notes in Computer Science, Vol. 1000. Springer-Verlag, Berlin Heidelberg New York

(1995)

8. Michaelsen, E., Meidow, J.: Basic Definitions and Operations for Gestalt Algebra. In:

Gurevich, I., Niemann, H., Salvetti, O. (eds.) Image Mining Theory and Applications. In-

stic Press, Portugal, ISBN 978-989-8111-42-5 (2009) 53-62.

9. Michaelsen, E., Stilla, U., Soergel, U., Doktorski L.: Extraction of building polygons from

SAR images: Grouping and decision-level in the GESTALT system. Pattern Recognition

Letters, to appear 2010, online under http://dx.doi.org/10.1016/j.patrec.2009.10.004 (2009)

10. Michaelsen, E., Arens, M., Doktorski, L.: Elements of a Gestalt Algebra: Steps Towards

Understanding Images and Scenes. In: Gurevich, I., Niemann, H., Salvetti, O. (eds.): Image

Mining Theory and Applications. Instic Press, Portugal, ISBN 978-898-8111-25-8 (2008)

65-73.

11. Nagao, M., Matsuyama, T.: A Structural Analysis of Complex Aerial Photographs. Plenum

Press, New York London (1980)

12. Porway, J., Wang, Q., Zhu, S. C.: A Hierarchical and Contextual Model for Aerial Image

Parsing. Int. J. Comput. Vis. DOI 10.1007/s11263-009-0306-1, online at Springerlink.com,

(2009)

13. Priese, L., Schmitt, F., Hering, N. (2009): Grouping of Semantically Similar Image Posi-

tions. In: Salberg, A-B., Hardeberg, J. Y., Jenssen, R. (eds.): SCIA 2009, Oslo, Norway,

June 15-18, Proceedings. Bd. 5575. (2009) 726--734

14. Sternberg, S.: Group Theory and Physics. Cambridge University Press (1995)

15. Stilla, U., Michaelsen, E., Soergel, U., Schulz K.: Perceptual Grouping of Regular Struc-

tures for Automatic Detection of Man-Made Objects Examples from IR and SAR. IGARS

2003, IEEE, 0-7803-7930-6, (2003)

16. Watson, B., Wonka, P. (Guest editors): Perceptual Methods for Urban Modeling. IEEE

Computer Graphics, Vol. 28, No. 3 (May/June 2008)

17. The e-TRIMS project. http://www.ipb.uni-bonn.de/projects/etrims/ (last accessed Februar

2010)