Pattern Recognition Imaging for AFM Measurements

Mario D’Acunto and Ovidio Salvetti

Instituto di Scienze e Tecnologia dell’Informazione, ISTI-CNR

via Moruzzi 1, I-56124, Pisa, Italy

Abstract. The focus of this paper is on an algorithm for distortion corrections

for atomic force microscope (AFM) recorded images. AFM is a fundamental

tool for the investigation of a wide range of mechanical properties due to the

contact interaction between the AFM tip and the sample surface. When a se-

quence to AFM images correspondent to the same area are recorded, it is com-

mon to observe convolution of thermal drift with surface modifications due to

the AFM tip stresses. The surface modifications are material properties and add

knowledge to the response of the materials on nanoscale. As a consequence, a

suitable de-convolution of the thermal drifts on the recorded images need to be

developed. In this paper, we present a method for correcting thermal drifts

where the original images are corrected using a low-order polynomial mapping

function. The precision achieved and the fast computation time required make

our method particularly useful for image analysis in a wide range of applica-

tions.

1 Introduction

In the last two decades atomic force microscope (AFM) has been developed well

beyond the topographic imaging tool. It has become an important instrument for ma-

nipulation and material property characterizations at the nanometer scale. The preci-

sion of positioning has always been the key driver for AFM technology and scanning

probe microscopy in general. In an imaging tool the uncontrolled hardware drift, such

as piezo creep and thermal drift, usually causes image distortion. Some solutions

based have been proposed [1-2]. The focus of this paper is to build a method for cor-

recting the thermal drifts that represent the most important source for distortions on

sequential recorded AFM images on the same localized area. The recorded data are

divided in two classes, one is connected to topographic data, and the second one to

elastic surface Young moduli. Such two channel AFM data give the possibility to

manipulate data crossing by one class (topography) to the other one (surface elastic

map). In special way, the method for image analysis based on drift compensation is

particularly useful for time AFM sequential measurements. This last technique is used

for studying the response of viscoelastic materials to AFM tip stress. The sample used

was a low molecular weight tri-block polycaprolactone-polyethilene glycol-

polycaprolactone (PCL-PEG-PCL) copolymers. Tri-block PCL-PEG-PCL copoly-

mers present generally hard islands surrounded by soft materials. Under the stress of

an AFM tip, it has been observed that soft polymer materials can cover the hard isl-

D’Acunto M. and Salvetti O. (2010).

Pattern Recognition Imaging for AFM Measurements.

In Proceedings of the Third International Workshop on Image Mining Theory and Applications, pages 68-77

DOI: 10.5220/0002962600680077

 SciTePress

ands. This wearing phenomenon for viscoelastic materials does not have a clear and

exhaustive explanation due to the difficult to quantify the soft polymer coating the

hard islands. Making use of the image analysis based on drift compensation it is poss-

ible to reduce the drift in sequential AFM measurements and calculate with accuracy

the soft polymer volume moved by AFM tip. Our method is divided in two steps. In

the first one, we identify using a cross correlation function the residual thermal drift.

In the second step, we introduce a function connected to the thermal drift and a set of

specific parameter connected to low-order polynomial mapping function. The mini-

mization of such mapping function leads to the optimal parameters removing the

drifts from the sequence of the AFM images of viscoelastic sample using an useful

pattern recognition matching the images correspondent to same sample areas recorded

in different times. Our proposed method should become a powerful tool for the accu-

rate analysis of stressed viscoelastic surface and accurate quantification of AFM mul-

tichannel measurements.

2 Numerical Methods for Image-based Adaptive Drift

Compensation

The possibility of investigation of surface properties of viscoelastic materials using

AFM is based essentially on a sequence of scans on the same area to be observed.

The interpretation of data is complicated by two main factors: i), the presence of

drifts does difficult to compare AFM images acquired in different times on the same

sample location; ii), the accurate identification of specific morphological deforma-

tions of viscoelastic materials due to stressing tip resulting in a modified sequential

images with respect to the first primitive image, so leading to misinterpreted data.

Since AFM generates multiple image channels simultaneously, the spatial and tem-

poral correlation of patterns in these channels can substantially enhance the robust-

ness of the pattern detection and its position measurement, see appendix. Further-

more, the raster scanning of a probe across the same pattern back and forth embeds

asymmetric feedback control signatures for widely contact mode imaging. These

signatures provide a powerful tool to distinguish a true pattern from a set of noisy

data. Reliable pattern positioning data enable a precise adaptive control which should

achieve a sub-nanometer positioning accuracy over long period of time. The forward

scan (trace) and the reverse scan (retrace) of the same location also provide indepen-

dent information of the same patter location. In this paper, we will consider two

channels correspondent to the topographic data (first channel, quantitative data) and

surface elastic Young moduli data (second one) measured using the modulation force

AFM tool. The topographic data correspond to the height z=f(x,y) measured by the

AFM tip scanning the sample surface, see figure 5 (left). On contrary, the modulation

force channel measures in a qualitatively way the differences of surface elasticity.

Modulation force is a powerful tool for the knowledge of surface properties, never-

theless when the AFM is used for a time sequence scanning cycle on the same viscoe-

lastic sample area, it is strongly limited by its qualitatively nature.

We adopt a new method integrating a numerical corrections of thermal drifts with

pattern recognition imaging. A cross correlation function is used a priori as a method

for the definition of the possible range of thermal drift to be identified. There are

mainly two approaches to connect pattern recognition with location of specific fea-

tures on multi-channel images: template based method or parametric one. Template

based algorithms locate regions on the image that matche a known reference pattern.

They bare applicable when well defined and slowly changing patterns are available

on the image. Multi-channel AFM images can improve pattern location accuracy by

matching all the channels of images with their own templates, while these templates

are spatially correlated, figg. 1-2. Parametric based algorithms can be applied when

focused patterns are changing from image to image and cannot be described by image

template. These patterns, however, can be indentified by a set of measurable variables

such as geometrical and regression properties that are restricted to a certain paramete-

rized region in the space of measured variables. Parametric algorithms based on geo-

metrical patterns and spatial correlation of combined AFM images have been devel-

oped to locate the surface pattern with sub-pixel resolution in real time [2]. It is com-

monly recognized that a robust and precise drift measurement tool based on imaging

patterns is needed in order to compensate thermal drift without causing positioning

errors. Kalman filter provides the best results when dynamics of the system is accu-

rate and noise statistical parameters are fixed and known a priori. Unfortunately, this

is not generally the case for AFM measurements where both dynamics and noise

statistics may change in time and depend on viscoelastic sample, tip and environment

(humidity, temperature, etc.). In this situation, with inaccurate model and/or underes-

timated statistical parameters of the noise, Kalman filter may diverge, i.e., its estima-

tion has errors that are much greater than predicted by theory [2]. The general chal-

lenge in image analysis of AFM measurements is to provide accurate and reliable

tools to precisely locate the imaging pattern and implement real time control accord-

ing to specific applications requirements.

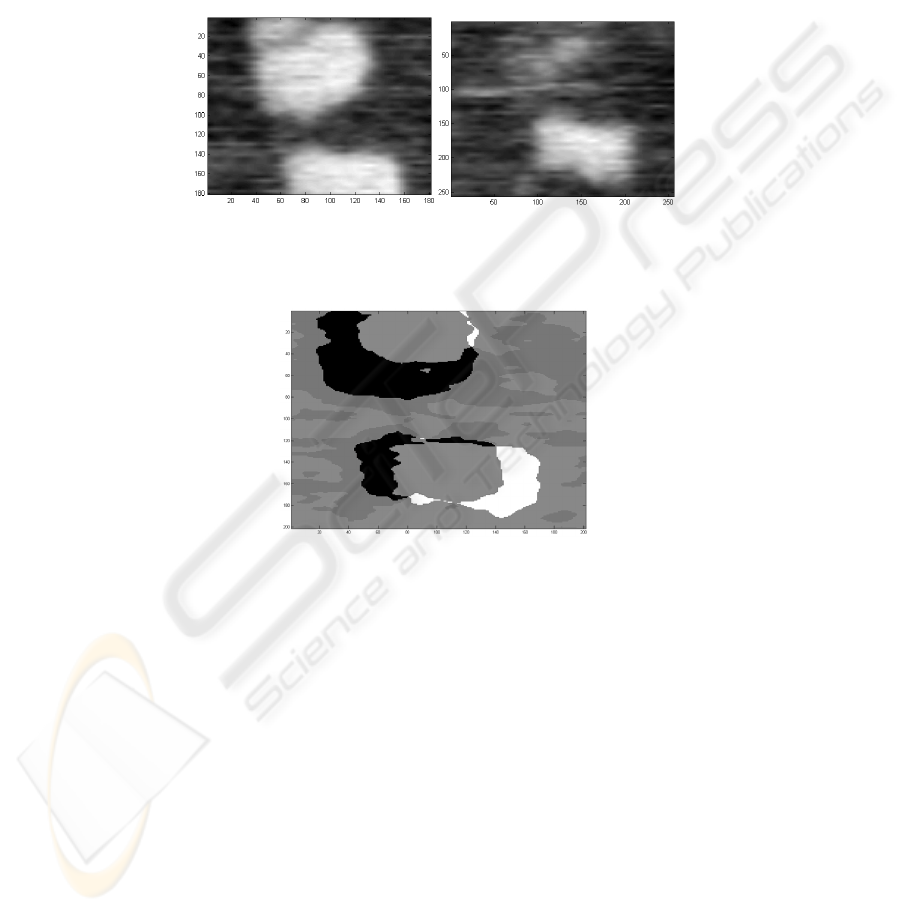
Fig. 1. A two channels AFM image of the tri-block PCL-PEG-PCL copolymer. On the contrary

to topographic data (left), the FMM image (right) shows characteristic hard domain (brighter)

surrounded by softer matrix (dark). The hard domains are approximately cylinders with the

principal axe normal to the surface. The zoom of the area surrounding the hard islands in the

Modulation force mode image are reported in the figure 2. The area considered was 1μm×1μm.

Fig. 2. Modulation Force (FMM) recorded data of 200nm×200nm areas showing two hard PU

islands (bright regions) surrounded by soft matrix (darker areas). From A-to-D: progressive

reduction of the stiff areas (white-to-grey) induced by the repeated passage of the AFM probe

tip.

2.1 A New Method for the Correction of AFM Drifts

The correction of drifts on viscoelastic AFM images is complicated by the overlap-

ping of surface effects due to tip stress that can drag polymer material from a site to

another one. As a consequence, if the displacement due to the drift, Δr, is known

during the scanning of an image, it should be possible to apply a correction based on

Δr(t) to the scanned image to recover an undistorted image. The correction can be

expressed as a mapping (x,y)→(x’,y’) between the set of points (x, y) in the image and

a new set of coordinates (x’,y’), based on the time each point was scanned. Generally,

the z-direction, i.e., the height would be not affected by relevant drifts, in special way

thermal drifts. This implies the brightness of any pixel can be considered as the “true”

value of the measurements. An other important feature of distortions is due to the

slow scanning axis. Generally, the slow scanning axis is the y-axis, while the fast

scanning axis is the x-axis. We can rewrite our mapping function (x,y)→(x’,y’) as

[3]:

)y(rxx

′

)y(ryy

′

(1)

Thermal changes is the main source for drifts on AFM image on viscoelastic ma-

terials, other distortions could arise by deformation of scanning tip or nonlinearity in

the xy stage or non-orthogonality between the x and y and z axes, can lead to position-

al errors that are functions of x and z. In our measurements, the incidence of such

distortion are not present, so we limit ourselves essentially to thermal drift. If thermal

drift is the main source drift, then changes of relative positions are not expected. If

the slow scanning is the y-axis, each horizontal can line may be shifted either up,

down, right, or left with respect to its neighbors, the scan line itself remains intact and

unchanged. This is because we only need to rescan a small vertical portion of the

original image and the displacement of each scan line at its center can be used as a

correction for the entire scan line.

Fig. 3. Overlapping of the first and the 30-th image recorded on the same location of the vis-

coelastic sample before treatment. The shift of the hard domains could be due to thermal drift

or specific viscoelastic features due to tip stressing. Our computational methods should be able

to discriminate between the two sources of shifting. The alignments were made using a cross

correlation function, eq. (3).

Because thermal drift is a slowly varying, smooth function, we can model it as a

low order polynomial along y-direction. For moderate drift a suitable third order

polynomial could work:

210

yAyAyAAxx ++++=

′

210

yByByBByy ++++=

′

(2)

Mathematically our target is the solution of the system equations (2), i.e., to find

the set of parameters [

, A

,…,B

] which, when applied to both the original scan

yields the minimum difference between the overlapping areas of two corrected im-

ages, as in figure 3. This problem is a main topics of the broad subject of image regis-

tration, an active area of research in computer science and numerical programming

[3-5]. In comparing two images, there are two broad strategies one could pursue: i)

comparing the two images pixel by pixel; or, ii), comparing specific lists of features

that have been identified in each of the images. The first strategy has the significant

disadvantage that there are many more pixels than identifiable features, leading to

algorithms that are computationally intensive and in some sense inefficient.

The alternative strategy requires some method for identifying the appropriate fea-

tures in the images, and this raises too many problematic issues for a method to be

applicable to any scanned image. In addition some surface effect due to stressing tip

on the viscoelastic sample can produce misunderstanding features using such strate-

gy.

Following Salmons et al. [3], we adopt a strategy based on pixel-to-pixel approach

introducing a minimum difference function, defined as the minimum root-mean-

square (rms) difference between the pixel value of the sequence of corrected images

and the sequence of original images. The sequence of corrected images is found ap-

plying a cross correlation function. The cross correlation function for two arrays

and

B of discrete data points is given by [6]:

() ()( )

,. ,.,

yC AijBixjy

ΓΔ Δ = +Δ +Δ

∑∑

(3)

where

) is the number of data per row (column) and C is a normalization con-

stant. The position (

y) of the maximum of the cross correlation function gives the

lateral shift of the images relative to each other. If the shapes of the two surfaces are

identical, the maximum lies at (0,0). To prevent the indices in the above formula from

running out of range, the performance of the cross correlation has to be restricted to a

smaller area inside the actual images leaving a border of the least the same size as the

expected image shift. Once the corrected images have been found with a cross corre-

lation function, eq. (3), we can minimize the set of parameters [

, A

,…B

], introduc-

ing the

diff-function defined as [3]:

[]

() ()

, ,..., , ,

01 3

diff function A A B z i j z i j

−=−

∑∑

⎡

⎤

⎣

⎦

(4)

where

z is the pixel value of an image at a particular point (i,j), z

and z

are the cor-

rected data image and the source (as recorded) data image, respectively. Eq. (4)

means that the mapping function (

x,y)→(x’,y’) to an area of the main image extending

beyond its own center, maximizing the area available for comparison between the two

corrected images. We have to find a global minimum of this function over the al-

lowed parameter space; in fact, there may be many local minima. A robust method is

based on using a grid search, where to evaluate the diff-function for all possible val-

ues of all eight parameters (that is, for all points an eight dimensional grid). Neverthe-

less, such method is too slow to be used on a sequence of images. In this paper we

present an alternative strategy based on an preview estimation of the most probable

couple (

) found as the maximum of the cross correlation function. Because the

shift is expected in the direction of the

x-direction, figure (4), we can select a strip

divided in different block numbered by

. A this point the diff-function can be limited

to three only parameters:

[]

()()

,, , ,

diff function x y z i x j y z i j

δδ

− Δ Δ = +Δ +Δ −

∑

⎡

⎤

⎣

⎦

(5)

with the precalculation made with cross correlation function, evaluating the differ-

ence function for each new set of parameters now consists of looking-up and sum-

ming a series of array values in

diff-function[

y], one for any block

. To mi-

nimize the overhead of this reevaluation, parameters lists are carefully sorted, so that

all possible parameter sets for each range of (

y) are exhausted before reevaluat-

ing

diff-function[

y].

The incidence of the thermal drift is the same on both the channel AFM data, to-

pography and surface elastic moduli. We have operates the correction drift on

Fig. 4. Scheme showing the identification of a possible shift described by a couple (

identified with a cross correlation function. On right the stripe containing the possible shift due

to thermal drift along the slow scanning direction.

the modulation force data, but we can use such information on the topographic data

where pattern recognition was rather hard to do. As a consequence, after undergoing

the adjustment procedure, the new surface images correspondent to the corrected

topographic data, denoted by

A* and B*, can be compared quantitatively. We quanti-

fied the amount of volume change between the subsequent recorded data. This has

been done by integrating over the difference of the image data correspondent to the

recognized area:

() ()

*, *,

VBijAij

Δ= −

∑

⎡

⎤

⎣

⎦

(6)

3 Results and Discussion

The algorithm for the correction of the drift in the AFM imaging sequence was car-

ried out in two steps. In the first step, the images had to be laterally adjusted using the

cross correlation function, eq. (3). The couple (

y) that maximizes the cross cor-

relation function was found [4]. In the second step, we applied the

diff-function re-

stricted to three parameters [3] to the sequence of recorded images. The application of

these two steps was justified by the fact that all the observed image shifts showed

translation movement and a small degree of rotation, figure 3, [6]. After undergoing

the adjustment procedures, the new surface images were compared quantitatively,

figures 5 and 6, and the degree of change in wear volume was calculated, figure 7.

The restricted

diff-function demonstrated to be an efficient and robust algorithm

for the minimization finding with respect to grid search. To have an idea how the

computation scales, suppose that the maximum amount of the distortion drift remains

constant ad a fraction of the image height (say, 5%), but that the number of pixels N

in the image is doubled. Maintaining single-pixel precision in the grid search requires

that the number of values of each of the parameters [

,…,B

] also be doubled. For

each set of parameters, the number of blocks in y-direction to be evaluated would also

be doubled. Thus for a third order polynomial fit, the grid search should scales as

O(N

). Practically, downsampling an image by a factor of two should cut the time of

the grid search by more than a factor of 100. Subdividing an image in two and cor-

recting each half independently would have a similar impact on computation time, but

would make the method less robust to image artifacts. To have an estimation of the

computation time achieved by our method, we timed our program on a single

256

×256 pixel image, running it on a desktop computer with a single Intel Core I7

processor running a 2.93GHz. The search for the couple (

y) using the cross cor-

relation function and then the minimization of the

diff-function [

y] on the

sequence of 30 images required approximately 22 s.

Fig. 5. Comparison between the first and 30-th scan after the correction of thermal drift. The

thermal drift is quantified by diff-function minimization as approximately 10nm, i.e., 5% of the

entire scanning length.

Fig. 6. This image is the equivalent of figure 3 after the correction of thermal drift using our

procedure algorithm. The overlapping of the first and the 30-th image recorded on the same

location of the viscoelastic sample present now a region of the hard island that has been coated

by the polymer. Analogously, a shift independent by thermal source is present indicating that

the hard island moved by the initial location due to reorganization of the polymer soft matrix.

If our results are confirmed by further studies and refinements of our algorithms, new insights

on the nanoscale dynamics of soft surface could be identified.

An important parameter that describes the tri-block copolymer sample surface

modifications induced by the AFM tip is the volume change between subsequent im-

ages [5]. The volume can be calculated by integrating over the difference following

the expression (6) using two subsequent acquired AFM images after adjustment. The

volume evaluation is performed on the topographic images once the drift are cor-

rected on the modulation force. The behaviour of the volume changes between subse-

quent images is shown in figure 7.

Fig. 7. Volume changes as calculated using eq. (2) between subsequent images. The volume is

calculated on topographic data correspondent to the re-aligned and computationally corrected

FMM images.

The volume variation between subsequent images presents a fast growth after an

activation barrier is reached. During the first scans the soft polymer component pre-

sents a resistance to tip induced stress. When the stress drops the activation, then the

volume percentage approaches to a sort of plateau with reduced fluctuations. It is

interesting as shoed by figure 6, that the hard islands shift position making so more

difficult for the soft component to coat the hard regions. All such results can be well

interpreted only after computational manipulation as above described. Many problem

are still open and they can be well known only after many dedicated experiments and

suitable computational algorithms. Our computational image analysis results seem go

in this direction.

4 Conclusions

The investigation of viscoelastic materials using AFM instrumentation is particularly

powerful to define the surface properties on molecular and supramolecular scale.

When a repeated sequence of AFM images on the same area, the images present a

convolution of thermal drifts and material-related modified features due to AFM tip

stressing. In this paper, we develop some algorithms for the accurate deconvolution

of thermal drift from the specific surface viscoelastic modifications. Our method

corrects the thermal drift using a low-order polynomial mapping function. The me-

thod is robust and requires short computation time, making suitable its shearing on a

wide range of applications where image analysis is required.

References

1. Yurov, V. Yu., Klimov, A. N.,: Scanning tunneling microscope calibration and reconstruc-

tion of real image: Drift and slope elimination. Rev. Sci. Instrum., 65 (1994) 1551-7

2. Clayton, G. M., Devasia, S.,: Image-based compensation of dynamic effects in scanning

tunneling microscopes. Nanotechnology 16 (2005) 809–818

3. Salmons, B. S., Katz, D. R., Trawick, M.L.,: Correction of distortion due to thermal drift in

scanning probe microscopy. Ultramicroscopy, available on line.

4. Gonzalez, R., Wood, R.,: Digital Image Processing. Upper Saddle River, NJ, Prentice Hall

(2008).

5. Colantonio, S., Gurevich, I. B., Salvetti, O.,: A two-step approach for automatic microscop-

ic image segmentation using fuzzy clustering and neural discrimination. Pattern Recogni-

tion and Image Analysis, 17 (2007) 428 - 437.

6. Lazzeri, L., Cascone, M.G., Narducci, P., Vitiello, N., D’Acunto, M., Giusti, P.,: Atomic

force microscopic wear characterization of biomedical polymer coatings. Tribotest, 12

(2006) 257-265.

Appendix: Background on AFM and Modulation Force Analysis

The technique for wear testing consisted in using the AFM probing tip to abrade the

surface of PU sample for approximately 30 scans while simultaneously imaging the

area where the polymer was being progressively damaged by the scanning tip.

The measurements were carried out making use of an Autoprobe CP AFM (Park

Scientific Instruments, Sunnyvale, CA) operating in contact mode. The measurements

were performed in air at room temperature and relative humidity, nearly 40%. Images

of different areas (256pixels

×256 pixels) were acquired using silicon tip (conical

shape, nominal probe radius of 10nm, nominal cantilever stiffness 0.24N/m, from PSI

manufacturer). Topographic images of square areas of 200nm

×200nm were acquired

with silicon microlevers with a spring constant of 0.24Nm

-1

, and nominal radius of

10nm. In addition to topography, mechanical properties qualitative information has

been stored making use of Force Modulation Microscopy (FMM) technique. FMM

operated in dynamic mode and allowed simultaneous acquisition of both topographic

and material-property data. It was used to detect surface elastic modulus variations on

which the image analysis was performed.

Fig. 8. On left, the schematic cartoon of an AFM. On the right, the sketch of a Force Modula-

tion Microscope (FMM). Gradients of elasticity can be record using modulation force imaging

(right) with the correspondent topography data.