
PARTIAL FEEDBACK MULTI-USER SCHEDULING
IN MULTI-ANTENNA SYSTEMS
Ahmad Suhail Salim
Electrical Eng. Dept., King Fahd University of Petroleum and Minerals (KFUPM)
P.O. Box 7626, Dhahran 31261Saudi Arabia
Keywords: MIMO, MIMO Scheduling, Partial Feedback.
Abstract: In this paper we consider the greedy scheduling algorithm that routes transmission of users’ packets based
on their reported CSI in the uplink channel to the user with the best instantaneous channel conditions. We
propose a scheduling scheme that relies on reporting partial feedback of the CSI. We compare the proposed
scheme to the one that uses perfect channel information at the base station, we will see that the proposed
scheme has significantly less complexity at the expense of a loss in the system’s capacity.
1 INTRODUCTION
In order to support services requiring high data rates
such as the Internet while ensuring the quality of
service (QoS), the spectral efficiencies of the next
generation of wireless networks has to be greatly
enhanced. The concept of multiple-input multiple-
output (MIMO) systems introduced in the mid 1990s
demonstrated that using multiple antenna elements
at both the receiver and the transmitter can result in
enormous capacity gains. Since then, various MIMO
architectures have been proposed such as space-time
block coding and smart antenna beamforming.
In multiuser environments, independence of
fading among users, called multiuser diversity, can
be exploited to increase the system capacity. Two
critical targets of packet scheduling are to maximize
the system capacity (throughput) and to offer
fairness among users. This is accomplished by
tracking the instantaneous channel quality of the
users in the system and schedule transmissions to the
user who has the best channel quality at any given
time. In this case the system is ‘riding the peaks’ of
channel qualities of all the users at all times.
In the case of greedy scheduling, the scheduling
scheme maximizes the system capacity through the
use of multiuser diversity. Specifically, each spatial
channel is allocated to a user with the best channel
condition for each time slot. Therefore, some users
in adverse channel conditions may not be served,
causing unfairness among users. While in the round
robin scheduling (RRS) scheme was studied for
MIMO cellular systems operated in a cyclic fashion
regardless of the channel conditions, and thus
achieves fairness among users.
Much of the work on multi-user MIMO channels
has assumed that the transmitter and receivers all
know the channel exactly. Accurate CSI may be
easy to obtain when the channel is changing slowly
(e.g., as in indoor scenarios), but it is much more
difficult in situations where the channel is changing
rapidly. An analysis of the penalty for using
imperfect or outdated feedback of channel
information would be of significant benefit to
system designers.
In this paper we propose a scheduling algorithm
that would require the users to report part of their
CSI back to the transmitter, where it then will decide
to route the transmission to the user with the best
effective SNR The key reason for this idea is to
reduce the traffic in the feedback path, so then it can
be used for other purposes, but the question is does
this sacrifice worth it, and what are the effects of
using such scheme on the capacity of the system,
and is it tolerable or not, such questions and other
more will be further discussed in this paper.
2 SYSTEM MODEL
The model we consider applies to the downlink of a
multiuser MISO wireless packet data system as
illustrated in Figure 1, where we assumed having a
single BTS of multi transmit antennas that provides
data services to M users, each of which is equipped
157
Salim A. (2010).
PARTIAL FEEDBACK MULTI-USER SCHEDULING IN MULTI-ANTENNA SYSTEMS.
In Proceedings of the International Conference on Wireless Information Networks and Systems, pages 157-160
DOI: 10.5220/0002966401570160
Copyright
c
SciTePress
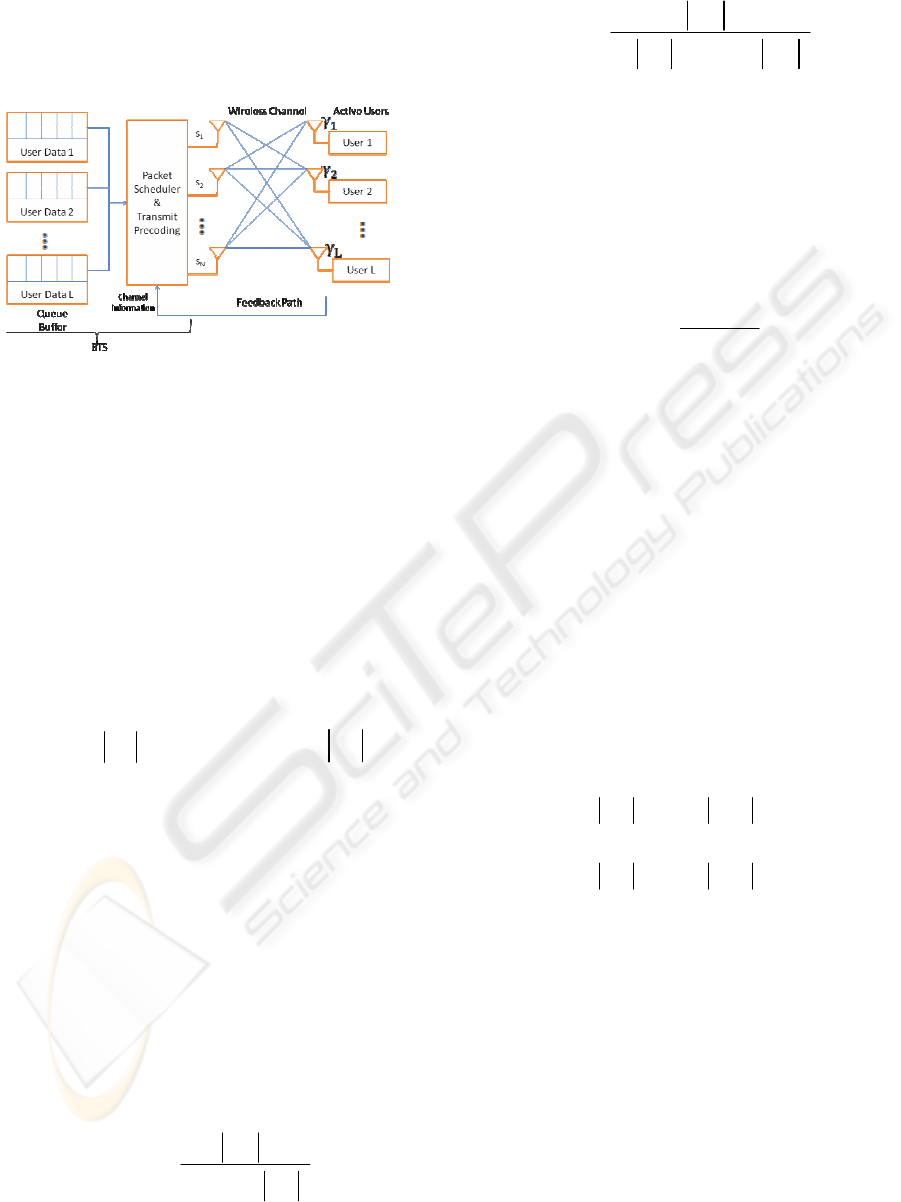
with a single antenna. Each user reports his channel
state information (CSI), using it and harnessing the
unequal latency property of the service to serve
multiple users with disparate SNRs.
Figure 1: Multiuser MISO model.
In the proposed partial feedback multiuser
scheduling each user will feedback only the
minimum and the maximum of his paths’ gains,
along with the number of the antenna that
corresponds to the maximum path gain of each.
For simplification purposes, we assume that the
M users experience the same average SNR and that
each link exhibits quasi-static frequency non-
selective (flat) fading so that the channel gains
remain constant throughout the transmission of one
data packet. According to the proposed scheduling
scheme each user will report the minimum and the
maximum of his paths’ gains, namely (for the ith
user):
2
() ()
min
1,2, ,
min
ii
j
jN
hh
, and
2
() ()
1,2,
max
,
max
ii
j
jN
hh
Where
()i
j
h is the complex fade coefficient for
the path from transmit antenna (j) to the receive
antenna of the ith user.
Each user also reports the antenna number that
corresponds to his maximum path gain, now each
user has chosen the most favourable antenna for
him, but more than one user could compete to get
the same antenna, here the antenna will select his
user by applying the following maximization rule:
Choose user i such that
1,2, ,
max
ii
BW
iM
(1)
where
i
B
is the best SINR of the i
th
user defined as
2
()
max
()
2
()
min
1( 1)
i
i
B
i
h
Nh
(2)
, and
i
W
is the worst SINR of the i
th
user defined as
2
()
max
()
22
() ()
min max
1(2)
i
i
W
ii
h
hNh
(3)
The best case of the SINR occurs when there is
one path with maximum gain
()
max
i
h , and (N-1) paths
with minimum gain
()
min
i
h .While the worst case for
SINR occurs when there are (N-1) paths with
maximum gain
()
max
i
h , and one path with minimum
gain
()
min
i
h . And in both cases the noise power is
normalized to unity.
Also we use the following maximization rules:
() ()
()
1,2, ,
max
ii
BW
i
iM
B
(4)
() () ()
1,2, ,
max ( )
ii i
BB W
iM
(5)
A special case in this context is if one antenna
was not selected by any user, then he would choose
the best user among those who weren’t chosen by
the other antennas.
Let’s start with the complete fading coefficients
matrix (h), defined as:
(1) ( )
11
(1) ( )
M
M
NN
hh
h
hh
(6)
But here we’re only interested in the magnitude of
those fading coefficients, so we define the
magnitudes matrix (
h
) as:
22
(1) ( )
11
22
(1) ( )
M
M
NN
hh
h
hh
(7)
Now, and because we’re only gone use the
maxima and minima of the fading coefficients of the
users, the receiver of each user will feedback to the
BTS only the maximum and minimum of his fading
coefficients, so now we form two matrices on for the
maximum of the gains of each user for, and the other
for minimum of the gains of each user for, defined
by:
(1) ( )
max
1,2, , 1,2, ,
(1) ( )
min
1,2, , 1,2, ,
max max
min min
M
jj
jN jN
M
jj
jN jN
hh h
hh h
(8)
And consequently we can find the best and worst
WINSYS 2010 - International Conference on Wireless Information Networks and Systems
158
SINR matrices:
(1) ( )M
BB B
(9)
(1) ( )M
WW W
(10)
Now, each antenna will select his best user from
those who were competing on it (i.e. who had their
maximum path gains with that antenna) by using the
maximization rule.
If we select the maximization by Eq(1) then
define:
(1) (1) () ()
DBW
MM
BW B W
(11)
With keeping the terms corresponding to the users
who selected the specified antenna and dropping the
others.
To calculate the capacity of the system, we
simply sum the capacities of the active links, for
each link the capacity in bits per second per Hertz
can be calculated using Shannon’s theorem:
2
log 1CSINR
(12)
Where the SINR in Eq(12) corresponds to the
user that has been chosen by the antenna, and it can
be calculated as follows:
2
()
2
()
1
1
i
j
i
j
N
i
k
k
kj
h
SINR
h
(13)
3 RESULTS AND DISCUSSION
Some computer analysis were conducted using
Matlab to quantify and qualify our analysis, these
analysis carried out comparative analysis between
systems employing different feedback schemes,
namely, the full feedback, and the partial feedback.
In the code that we implemented, many sample
functions were generated for the capacity, and then
they were averaged for each value of the Mean SNR.
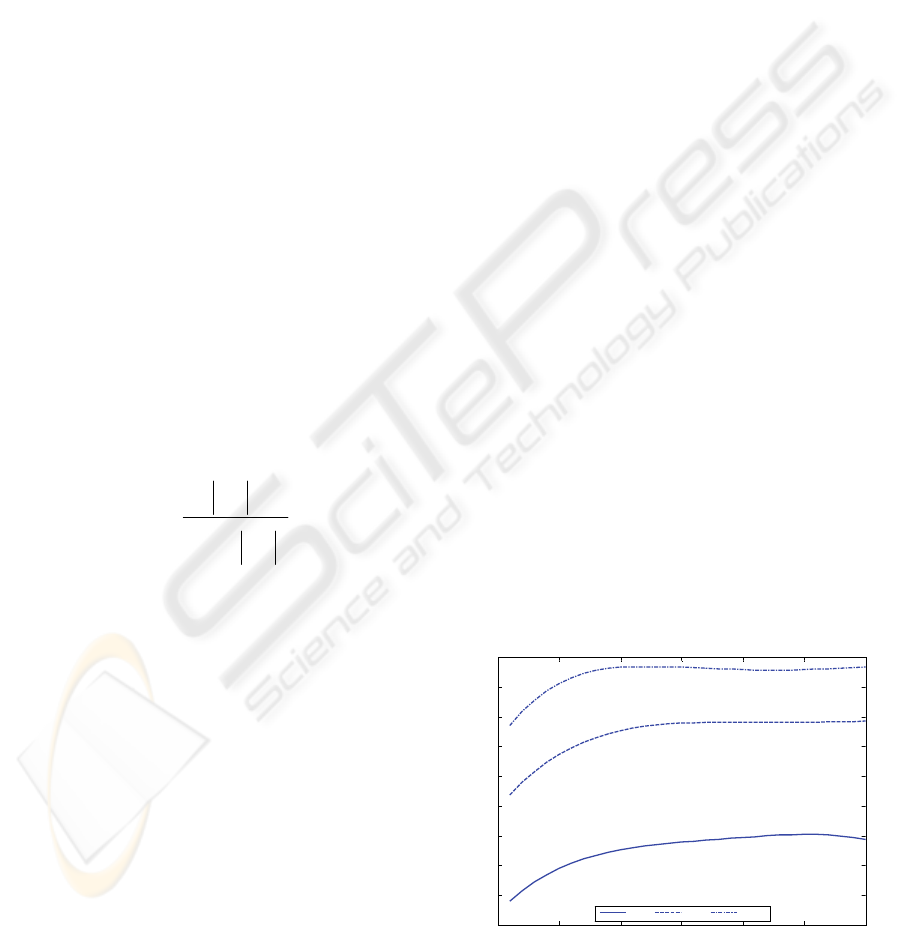
In Figure 2, the capacity is plotted versus the
mean SNR for various values for the number of
active users (M), with setting the number of transmit
antennas (N) to 4. From the Figure , it is observed
that the proposed scheme provides higher capacity
when the number of users is larger. This is expected
since as the number of users increases, it is more
likely that the base station schedules the users
experiencing little interference from the other users.
In addition, it is observed that the rate of increase of
the capacity for larger number of users is greater
since that’s because we’re assuming multichannel
MUD in which the scheduling scheme exploits
degrees of freedom in the channel.
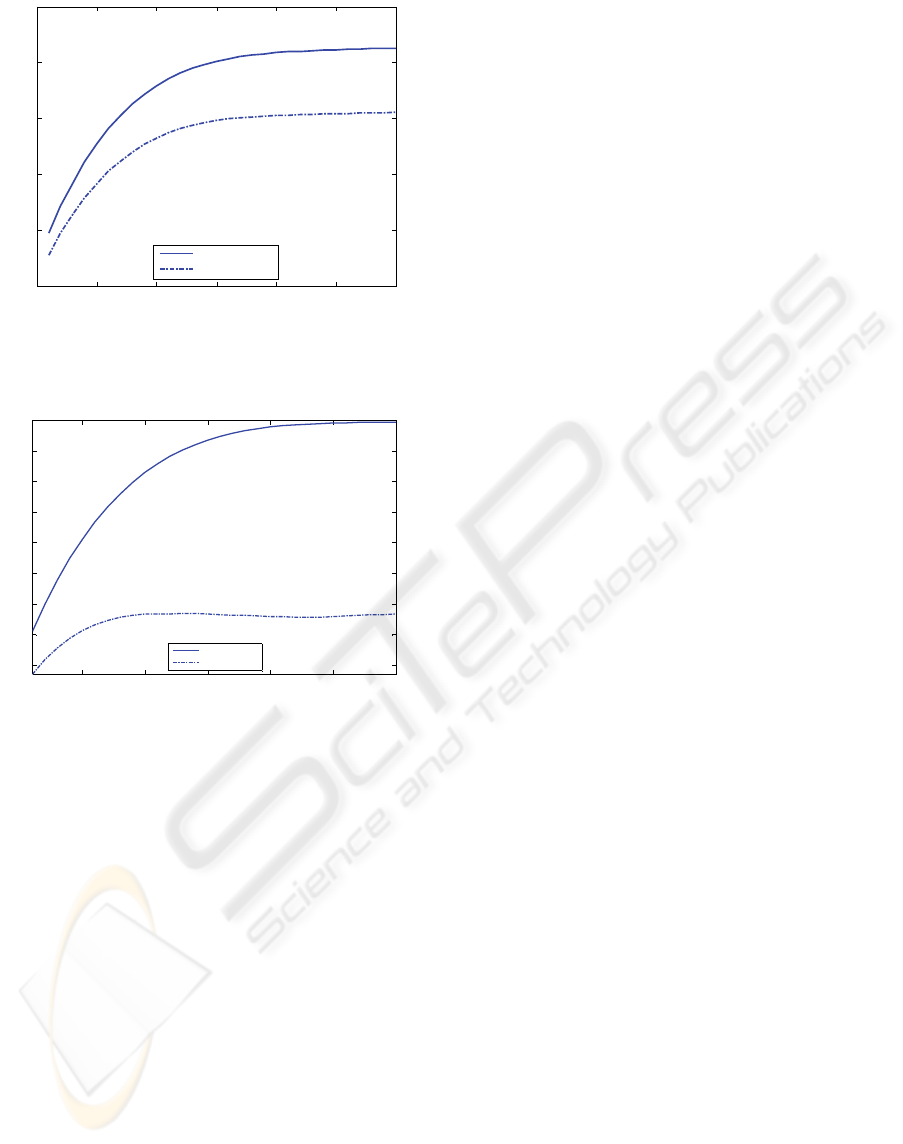
In Figure 3, the capacity of the greedy scheduling
with partial feedback is compared to that of the full
feedback when the number of active users (M) is 10,
with setting the number of transmit antennas (N) to
4, where it appears that the capacity is in the case of
partial feedback is less than that in the case of full
feedback, and we also note that the difference
between the two curves grows larger with increasing
the average signal to noise ratio.
It is also observed that for a given number of
users, as the SNR increase, the capacity becomes
limited since the system is interference limited at
high SNR.
In Figure 4, the capacity of the greedy scheduling
with partial feedback is compared to that of the full
feedback when the number of active users (M) is
100, with setting the number of transmit antennas
(N) to 4. It is noted that the capacity in the case of
partial feedback is much less than that in the case of
full feedback, that’s because in the case of full
feedback we have full knowledge of the channel and
so the scheduler will make correct decisions almost
all the time , while in the case of partial feedback, as
some of the CSI is not reported then the scheduler
will tend to choose users who are not actually the
best users, and then assign them to be the best users
and route the transmission for them, and this will
lead to a loss in the advantage that we gained from
having the transmission routed to users with better
channel conditions much often than the others.
0 5 10 15 20 25 30
2.5
3
3.5
4
4.5
5
5.5
6
6.5
7
SNR
(
dB
)
Capacity (bits/s/Hz)
M=10 M=50 M=100
Figure 2: Capacity of the partial feedback scheme versus
the mean SNR for various numbers of active users, M=10,
M=50, and M=100.
PARTIAL FEEDBACK MULTI-USER SCHEDULING IN MULTI-ANTENNA SYSTEMS
159
0 5 10 15 20 25 30
3.5
4
4.5
5
5.5
6
SNR(dB)
Capacity (bits/s/Hz)
Full feedback
Partial feedback
Figure 3: Capacity versus the mean SNR for full and
partial feedback multiuser scheduling when the number of
active users M=10.
5 10 15 20 25 30
6
6.5
7
7.5
8
8.5
9
9.5
10
SNR
(
dB
)
Capacity (bits/s/Hz)
Full feedback
Partial feedbck
Figure 4: Capacity versus the mean SNR for full and
partial feedback multiuser scheduling when the number of
active users M=100.
When the number of antennas is set to 4 and the
number of active users is 10, the three maximization
rules were tested and they provided similar results in
terms of the mean squared error, which was found to
be about 0.246, which is surely dependent upon the
parameters set in the Matlab code, and the MSE
would change if they were changed.
To judge whether this loss in the capacity is
tolerable or not, we need to look closer at the
application in hand, where some applications will
tolerate it, and others won’t, but in general the loss
in the capacity seems to be acceptable when the
number of active users is small, while it is
unacceptable when the number of active users is
large. A significant advantage of this method, is that
whatever the number of the transmit antennas, the
user will still send only two of his paths’ fading
coefficients, which is much less than sending N
fading coefficients by each user in the case of full
feedback, and this would be extremely useful in the
forthcoming generations of MIMO systems, where
systems using large number of transmit antennas
will be used much often.
Another advantage that is a sequence of the latter
is saving the power and increasing the battery life
for the user equipment, Also, the uplink path can
now handle more traffic for other applications.
According to that we can propose a dynamic
greedy scheduling that would give us the advantages
of both full feedback and partial feedback in the
same time. This could be done by setting the system
such that if there is high traffic on the downlink
channel, the BTS would prompt the users to report
full CSI, while if there’s high traffic on the uplink
channel, the BTS would prompt the users to report
partial CSI.
4 CONCLUSIONS
The capacity of the system when using partial
feedback was compared to that when perfect CSI is
used, the results proved that there is a small
reduction in the capacity when the number of active
users is small, this reduction increases when the
number of active users becomes larger, i.e. regarding
the capacity, partial feedback is inferior to full
feedback when the number of active users is large.
At the end, we state that the proposed scheme can
significantly reduce the complexity at the expense of
a small loss in the system’s capacity.
REFERENCES
R. Gozali, R. M. Buehrer and B. D. Woemer, “The impact
of Multiuser Diversity on Space-Time Block Coding:”
IEEE Commun. Lett., vol. 7, Issue 5, pp. 213-215,
May, 2003.
Sulyman, Ahmed, and Ibnkahla, Mohamed, “Performance
Analysis of Multiuser Diversity in MIMO Channels”,
Electrical and Computer Engineering, 2004, canadian
confernce, Vol 2, pp.1199–1202, May 2004.
Aktas, D., El Gamal, H, “Multiuser Scheduling for MIMO
Wireless Systems” Vehicular Technology Conference,
Volume 3, Oct. 2003.
WINSYS 2010 - International Conference on Wireless Information Networks and Systems
160
