
A NUMERICAL COMPARISON BETWEEN LSSTC AND VBLAST IN
WIRELESS SYSTEMS
Ahmad S. Salim, Salam A. Zummo and Samir N. Al-Ghadhban
Electrical Eng. Dept., King Fahd University of Petroleum and Minerals (KFUPM), Dhahran 31261, Saudi Arabia
Keywords:
Layered steered space-time codes, LSSTC, VBLAST, Capacity, Symbol error rate.
Abstract:
In this work we evaluate a recently proposed multiple-input multiple-output (MIMO) system called the
Layered Steered Space-Time Codes (LSSTC) that combines the benefits of vertical Bell Labs space-time
(VBLAST) scheme, space-time block codes (STBC) and beamforming. This evaluation is done by comparing
the capacity and the error rate of LSSTC to the well-known MIMO system, known as VBLAST. For that, we
derive a formula for the instantaneous capacity of single-user LSSTC. In addition, an adaptive scheme that is
based on LSSTC and VBLAST systems is proposed. This scheme selects the configuration and the modulation
scheme in order to improve the performance.
1 INTRODUCTION
Various techniques have been proposed to counter the
problem of propagation conditions, and to achieve
data rates that are very close to the Shannon limit.
One of these techniques is using MIMO systems
which uses antenna arrays at both the transmitter and
the receiver. Wolniansky et al. has proposed in (Wol-
niansky et al., 1998) the well-known MIMO scheme,
known as VBLAST. In VBLAST architecture, paral-
lel data streams are sent via the transmit antennas at
the same carrier frequency.
While MIMO systems as VBLAST can improve
the system capacity greatly, it is difficult to imple-
ment antenna arrays on hand-held terminals due to
size, cost and hardware limitation(Alamouti, 1998),
also it has poor energy performance and doesnt fully
exploit the available diversity. In order to overcome
these problems, Alamouti has presented in (Alamouti,
1998) a new scheme called STBC with two trans-
mit and one receive antennas that provides the same
diversity order as maximal-ratio receiver combining
(MRRC) with one transmit and two receive anten-
nas. With the tempting advantages of VBLAST and
STBC, many researchers has attempted to combine
these two schemes to result in a multilayered architec-
ture called MLSTBC (Mohammad et al., 2004) with
each layer being composed of antennas that corre-
sponds to a specific STBC. This combined scheme
arises as a solution to jointly achieve spatial multi-
plexing and diversitygains simultaneously. With ML-
STBC scheme, it is possible to increase the data rate
while keeping a satisfactory link quality in terms of
symbol error rate (SER).
In (El-Hajjar and Hanzo, 2007) beamforming was
combined with MLSTBC to produce a hybrid system
called the layered steered space time codes(LSSTC).
The addition of beamforming to MLSTBC further im-
proves the performance of the system by increasing
the antenna gain in the direction of the desired user,
while reducing it towards the interfering users. In
this paper, we show the superiority of LSSTC over
VBLAST by comparing their capacity and SER. Also
wee derive a formula for the instantaneous capacity of
a single-user LSSTC system. In addition, an adaptive
scheme based on LSSTC and VBLAST systems is
proposed. This scheme selects the configuration and
the modulation scheme to improve the performance.
2 SYSTEM MODEL OF LSSTC
Figure 1 shows the block diagram of a single-user
LSSTC system proposed in (El-Hajjar and Hanzo,
2007). The system has N
T
total transmitting anten-
nas and N
R
receiving antennas and is denoted by an
N
T
× N
R
LSSTC. The antenna architecture employed
in Figure 1 has M transmit adaptive antenna arrays
(AAs) spaced sufficiently far apart in order to experi-
ence independent fading and hence achieve transmit
diversity. Each of the AAs consists of L elements that
are spaced at a distance of d = λ/2 to ensure achiev-
161
S. Salim A., A. Zummo S. and N. Al-Ghadhban S. (2010).
A NUMERICAL COMPARISON BETWEEN LSSTC AND VBLAST IN WIRELESS SYSTEMS.
In Proceedings of the International Conference on Wireless Infor mation Networks and Systems, pages 161-164
DOI: 10.5220/0002970401610164
Copyright
c
SciTePress
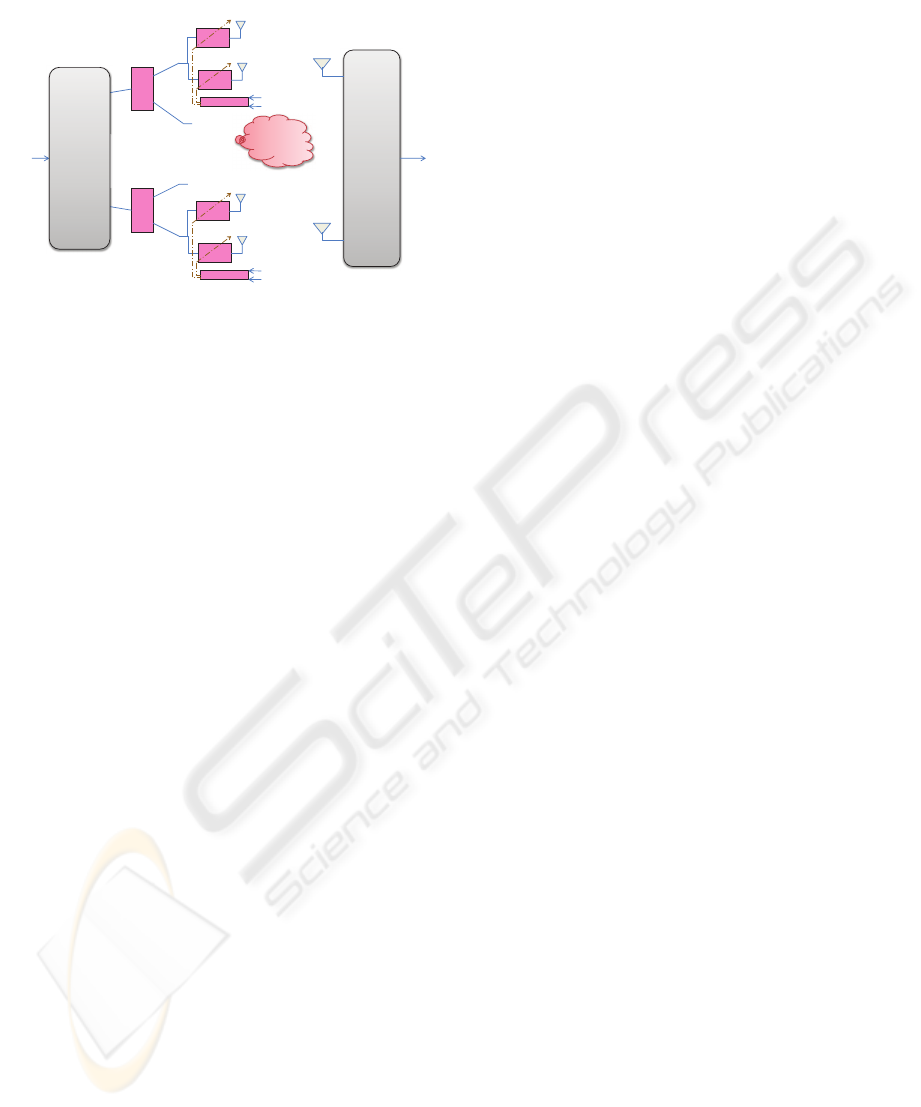
ing beamforming. A block of B input information bits
LSSTC
processing:
estimate a
and decode
STC 1
1
2
K
B
B
B
B
é ù
ê ú
ê ú
=
ê ú
ê ú
ê ú
ë û
M
1
B
Rich
scattering
environment
1
m
AA
b
1L
Beamformer
b
11
M
DOA
1
AA
STC K
K
B
M
M
M
1
Rx
R
N
Rx
M
M
B
Vector Encoder:
Serial to Parallel
Converter
Tx data
of length B
Rx data
b
ML
Beamformer
b
M1
M
DOA
M
AA
M
( 1)
K
M m
AA
- +
Figure 1: Block diagram of a single user LSSTC system.
is sent to the vector encoder of LSSTC and serial-to-
parallel converted to produce K streams (layers) of
length B
1
,B
2
,...,B
K
, where B
1
+ B
2
+ ··· + B
K
= B.
Each group of B
k
bits, k ∈ [1,K], is then encoded by
a component space-time code STC
k
associated with
m
k
transmit AAs, where m
1
+ m
2
+ ··· + m
K
= M.
The output of the k
th
STC encoder is a m
K
× l code-
word, c
i
, that is sent over l time intervals. The space-
time coded symbols from all layers can be written as
C = [c
1
,c
2
,...,c
K
]
T
, where C is an M × l matrix.
The coded symbols from C are then processed by
the corresponding beamformers, and then transmitted
simultaneously over the wireless channels. The trans-
mit antennas of all the groups are synchronized and
allocated equal power. Moreover, the total transmis-
sion power is fixed, where the transmitted symbols
have an average power of P
T
= 1, where the average is
taken across all codewords over both spatial and tem-
poral components. For the LSSTC system to operate
properly, the number of receive antennas N
R
should
be at least equal to the number of layers K.
We formulate the system model as follows. The
channel model is a MIMO quasi-static Rayleigh flat-
fading channel with N
T
transmit antennas and N
R
re-
ceive antennas. The quasi-static assumption indicates
that the channel gain coefficients remain constant for
the duration of the STBC block and change inde-
pendently for each STBC block. The flat-fading as-
sumption allows each transmitted symbol to be rep-
resented by a single-tap in the discrete-time model
with no inter-symbol interference (ISI). We assume
independent Rayleigh coefficients, i.e.,fading coef-
ficients are independent and identically distributed
(i.i.d.) circular-complex normal random variables
with zero-mean and 0.5 variance per dimension, ab-
breviated as C N (0, 1). The correlation caused by the
small distance separation is approximately removed
using the beamforming processing as we will show in
this Section..
The system model can be described in matrix no-
tation, where the received baseband data matrix Y can
be expressed as
Y = HWC+ N, (1)
where Y is the received signal over l time intervals
and has a dimension of N
R
× l, H is an N
R
× M ma-
trix whose entries are h
n,m
, and N is an N
R
× l matrix
that characterizes the additive white Gaussian noise
(AWGN). The n
th
row of N denoted as z
n
, where
n ∈ [1,...,N
R
], is a row vector of l columns, the i
th
en-
try of z
n
is a spatially uncorrelated circular-complex
normal random variable, and can be written as z
i
n
=
z
i
I,n
+ jz
i
Q,n
, where z
i
I,n
and z
i
Q,n
are two independent
zero-mean Gaussian random variables having a vari-
ance of N
0
/2, we will represent z
i
n
as C N (0,N
0
).
Furthermore, W is an M × M diagonal weight ma-
trix, whose diagonal entry w
m,m
is the L-dimensional
beamforming weight vector for the m
th
beamformer
AA and the n
th
receive antenna, and can be written as
w
m,m
= [b
m1
,··· ,b
mL
], where b
mi
, i ∈ [1, . . . , L], is the
i
th
weighting gain of the m
th
AA. The received signal
Y can be written in matrix form as
y
1
y
2
.
.
.
y
N
R
=
h
1,1
w
1,1
·· · h
1,M
w
M,M
h
2,1
w
1,1
·· · h
2,M
w
M,M
.
.
.
.
.
.
.
.
.
h
N
R
,1
w
1,1
·· · h
N
R
,M
w
M,M
c
1
c
2
.
.
.
c
K
+
z
1
z
2
.
.
.
z
N
R
. (2)
The beamforming vector w
m,m
is given by (Shu et al.,
2007) as w
m,m
= d
∗
n,m
, where the superscript
∗
repre-
sents the conjugate of the matrix. Refering to (2), a
modified channel matrix is defined as
ˆ
H =
h
1,1
w
1,1
··· h
1,M
w
M,M
h
2,1
w
1,1
··· h
2,M
w
M,M
.
.
.
.
.
.
.
.
.
h
N
R
,1
w
1,1
··· h
N
R
,M
w
M,M
, (3)
where
ˆ
H is the reconstructed channel matrix compris-
ing the MIMO fading channel and the DOA informa-
tion. Note that we assumed that the nulling vector
for all the paths corresponding to one AA (w
m,m
) is
the same. This follows from the assumption that the
separation between the receive antennas is much less
than the distance between the AA and the receiver,
then roughly speaking, they will have the same direc-
tion of arrival, which will result in having the same
nulling vector.
According to Equation (2) Y can be rewritten as:
Y =
ˆ
HC+ N. (4)
The channel coefficient
ˆ
H
n,m
can roughly ex-
WINSYS 2010 - International Conference on Wireless Information Networks and Systems
162
pressed as
ˆ
H
n,m
= h
n,m
w
m,m
= α
n,m
· [d
n,m
]
T
[d
n,m
]
∗
(5)
= L· α
n,m
.
Therefore the received signal can be expressed as in
(El-Hajjar and Hanzo, 2007):
Y = L
˜
HC+ N, (6)
where
˜
H is an (N
R
× M) matrix whose entries are
α
n,m
. Looking at (6), the effect of beamforming can
be clearly seen, which is a direct SNR gain.
3 CAPACITY OF LSSTC
The system capacity of VBLAST is given by (Mo-
hammad et al., 2004) as
C
VBLAST
= N
T
min
i=1,2,...,N
T
log
2
1+
SNR
N
T
kW
ZF,i
k
2
,
(7)
where SNR is the average signal-to-noise ratio, and
kW
ZF,i
k
2
is the squared Frobenius norm of the zero-
forcing projection row for the i
th
layer.
To derive a formula for the capacity of LSSTC per
user, we will follow the derivation of (Al-Ghadhban
et al., 2005). First, the instantaneous capacity was
found in (Sandhu and Paulraj, 2000) for an orthogonal
STBC with M
s
transmit antennas and R
s
code rate,
C
STBC
= R
s
· log
2
1+
P
T
M
s
kHk
2
(8)
In MLSTBC which is a combination of VBLAST
and STBC, an outage occurs if an outage happens
in any layer because all the STBC encoders (layers)
are transmitting at the same rate. The layer that is
the most probable to fall in an outage is the weakest
layer, i.e. the one that has the least value of kH
i
k
2
,
i = 1,2, . . . ,K, where H
i
is the i
th
matrix of H. There-
fore, the instantaneous capacity of a K layered STBC
system with a sub-stream SNR of ρ can be written as:
C = K · R
s
· log
2
1+ ρ· min
k=1,2,...,K
kH
i
k
2
= K · R
s
· min
k=1,2,...,K
log
2
1+ ρ·kH
i
k
2
.(9)
Extending the last results, the instantaneous capacity
of LSSTC can be expressed as:
C
LSSTC
= KR
s
min
k=1,2,...,K
log
2
1+
L
2
· P
T
M · N
0
· kH
PP,k
k
2
(10)
where H
PP,k
is the Post-Processing (PP) matrix cor-
responding to the k
th
layer after nulling out the in-
terference from the yet-to-be-detected layers. It is
clear that the LSSTC capacity is dominated by the
worst group which has the minimum value of H
PP,k
,
k = 1, 2,...,K.
4 NUMERICAL RESULTS
In all the Monte-Carlo simulations conducted in this
work, we used Alamouti’s STBC matrix of unity rate
for the STBC encoders in each layer. In addition, un-
less otherwise mentioned, non-ordered serial group
interference cancelation (SGIC) detector is used.
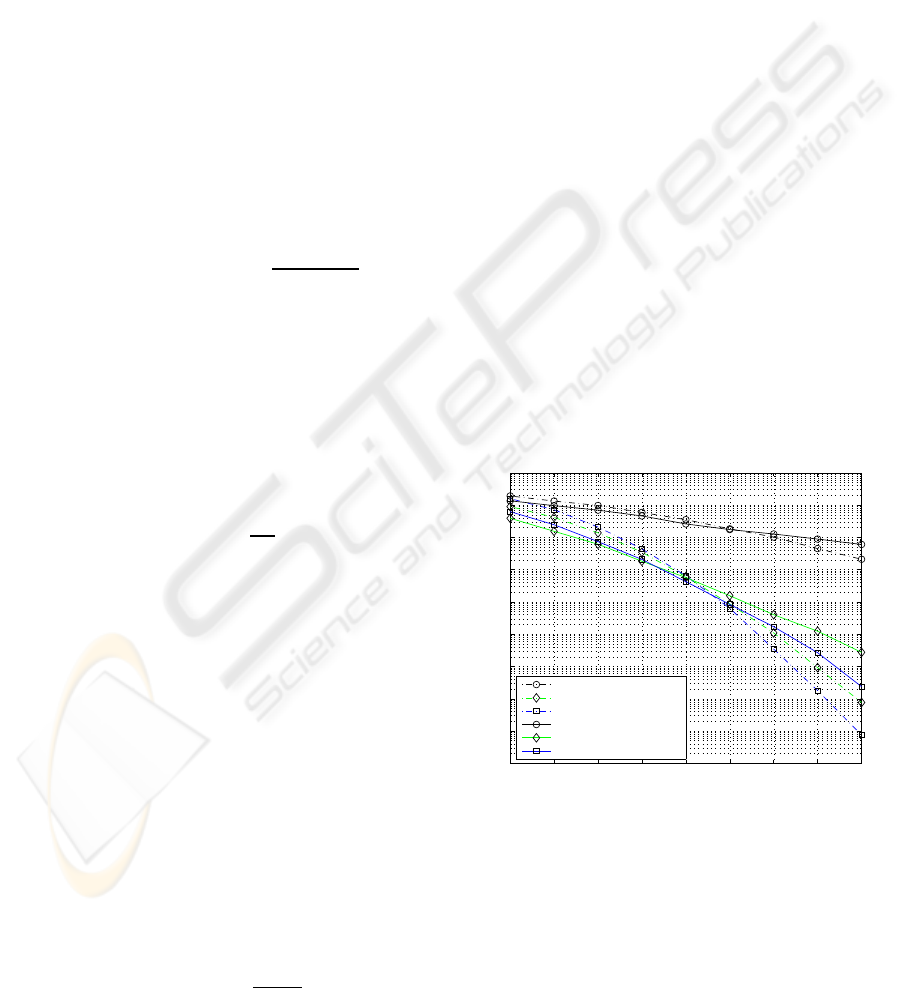
Figure 2 shows a fair comparison between LSSTC
and VBLAST in terms of the symbol error rate. The
two systems use a total number of transmit anten-
nas, N
T
= 8, and the receiver is equipped with 4 an-
tennas. In this comparison we have also compared
many transmitter configurations, in each a different
modulation scheme is used such that the spectral ef-
ficiency would be the same for all of them, which is
set to 4 bps/Hz. From Figure 2 it can be clearly seen
that VBLAST outperforms LSSTC in the low range
of SNR, whereas for values of SNR that exceed 9
dB, the LSSTC outperforms VBLAST because it has
a higher diversity order resulting from using STBC,
which drives the SER to decay sharply. Next, we pro-
0 2 4 6 8 10 12 14 16
10
−9
10
−8
10
−7
10
−6
10
−5
10
−4
10
−3
10
−2
10
−1
10
0
↑
(1)
↑
(2)
E
s
/N
0
(dB)
SER
LSSTC (BPSK K= 4, L= 1)
LSSTC (QPSK K= 2, L= 2)
LSSTC (16 QAM K= 1, L= 4)
VBLAST (BPSK K= 4, L= 2)
VBLAST (QPSK K= 2, L= 4)
VBLAST (16 QAM K= 1, L= 8)
Figure 2: SER of LSSTC employing non-ordered SGIC
at 4 bps/Hz and different modulation schemes with N
T
=
8 & N
R
= 4 (comparing VBLAST to LSSTC fairly).
pose an adaptive transmission scheme that selects the
configuration and the modulation scheme in order to
improve the performance. Table 1 lists the proposed
transmitter configuration and modulation scheme de-
pending on the SNR level. The adaptive scheme can
be designed using an antenna array with the capability
A NUMERICAL COMPARISON BETWEEN LSSTC AND VBLAST IN WIRELESS SYSTEMS
163

Table 1: Proposed Tx. and modulation configuration.
SNR level (dB) configuration Modulation
< 6.6 VBLAST QPSK
6.6− 9.2 VBLAST 16-QAM
> 9.2 LSSTC 16-QAM
−15 −10 −5 0 5 10 15 20 25 30
0
5
10
15
20
25
30
E
s
/N
0
(dB)
Capacity (bits/s/Hz)
LSSTC (K= 4 L= 1)
LSSTC (K= 2 L= 2)
LSSTC (K= 1 L= 4)
VBLAST (K= 4 L= 2)
VBLAST (K= 2 L= 4)
VBLAST (K= 1 L= 8)
Figure 3: Outage Capacity vs. E
s
/N
0
for an 8× 4 MIMO at
10% Outage probability, and 15 dB average SNR (compar-
ing VBLAST to LSSTC fairly).
of electronically activating specific antenna elements
and deactivating the remaining ones. This is done to
meet the antenna separation conditions of each mode
in the multi-configuration system. In LSSTC, there
are two conditions for the antenna element separation.
(1) The AAs should be sufficiently far apart in order
to experience independent fading. (2) Beamforming
elements within each AA should be spaced at small
distance (less than λ/2) to achieve beamforming. On
the other hand, VBLAST requires all the antennas to
be spaced sufficiently far from each other.
Figure 3 fairly compares LSSTC to VBLAST in
terms of the outage capacity of an 8 × 4 MIMO us-
ing non-ordered SGIC at 15 dB average SNR. Sev-
eral configuration are considered, and the capacity is
plotted versus E
s
/N
0
. As it can be seen from the fig-
ure, the capacity is approximately linearly increas-
ing with increasing E
s
/N
0
. It is clear to see that
VBLAST outperforms LSSTC, which is actually ex-
pected, since VBLAST is a pure spatial multiplexing
unlike LSSTC, where some antennas are assigned for
diversity. An adaptivesystem can be designed to max-
imize the capacity for all values of SNR. For the fore-
mentioned configuration we choose the single-layer
VBLAST system for the first range (-15 dB up to 1
dB), and for the second range (1 dB up to 20 dB) the
dual-layer VBLAST system gives the highest capac-
ity. If the SNR lies in the last range(>20 dB), then
using either LSSTC or VBLAST with 4 layers will
have approximately the same capacity. However, Fig-
ure 2 shows that LSSTC has a lower SER in the last
range, and therefore, choosing LSSTC is better.
5 CONCLUSIONS
In this paper,we evaluated the performanceof LSSTC
by comparing it to VBLAST. Also an adaptive sys-
tem that selects between LSSTC and VBLAST was
proposed. This study showed that combining beam-
forming, STBC, and VBLAST in LSSTC has better
performance than VBLAST at high SNR range.
ACKNOWLEDGEMENTS
The authors like to thank King Fahd University of
Petroleum and Minerals and KACST for their support
under grant no. SB070005 and NSTIP grant no. 08-
ELE39-4.
REFERENCES
Al-Ghadhban, S., Buehrer, R., and Woerner, B. (2005).
Outage Capacity Comparison of Multi-Layered STBC
and V-BLAST Systems. Vehicular Technology Con-
ference, IEEE 62nd, 1:24–27.
Alamouti, S. (1998). A Simple Transmit Diversity Tech-
nique for Wireless Communications. Selected Areas
in Communications, IEEE Journal on, 16(8):1451–
1458.
El-Hajjar, M. and Hanzo, L. (2007). Layered steered space-
time codes and their capacity. IEEE Electronics Let-
ters, pages 680–682.
Mohammad, M., Al-Ghadhban, S., Woerner, B., and Tran-
ter, W. (2004). Comparing Decoding Algorithms
for Multi-Layered Space-Time Block Codes. IEEE
SoutheastCon Proceedings, pages 147–152.
Sandhu, S. and Paulraj, A. (2000). Space-Time Block
Codes: a Capacity Perspective. Communications Let-
ters, IEEE, 4(12):384–386.
Shu, F., Lihua, L., Xiaofeng, T., and Ping, Z. (2007). A Spa-
tial Multiplexing MIMO Scheme with Beamforming
for Downlink Transmission. IEEE Vehicular Technol-
ogy Conference, pages 700–704.
Wolniansky, P. W., Foschini, G. J., Golden, G. D., and
Valenzuela, R. A. (1998). V-BLAST : An Architec-
ture for Realizing Very High Data Rates Over the
Rich-Scattering Wireless Channel. URSI Interna-
tional Symposium on Signals, Systems and Electron-
ics, pages 295–300.
WINSYS 2010 - International Conference on Wireless Information Networks and Systems
164
