MODELING LARGE SCALE MANUFACTURING PROCESS FROM
TIMED DATA
Using the TOM4L Approach and Sequence Alignment Information for Modeling
STMicroelectronics’ Production Processes
Pamela Viale
1,2
, Nabil Benayadi
1
, Marc Le Goc
1
and Jacques Pinaton
2
1
LSIS, Laboratory for Information and System Sciences,University of Marseille, Marseille, France
2
STMicroelectronics, Rousset, France
Keywords:
Process model discovery, Temporal knowledge discovering, Markov processes, Sequence alignment.
Abstract:
Modeling manufacturing process of complex products like electronic chips is crucial to maximize the quality of
the production. The Process Mining methods developed since a decade aims at modeling such manufacturing
process from the timed messages contained in the database of the supervision system of this process. Such
process can be complex making difficult to apply the usual Process Mining algorithms. This paper proposes
to apply the TOM4L Approach (Timed Observations Mined for Learning) to model large scale manufacturing
processes. A series of timed messages is considered as a sequence of class occurrences and is represented
with a Markov chain from which models are deduced with an abductive reasoning. Because sequences can
be very long, a notion of process phase is introduced. Sequences are cut based on the concept of class of
equivalence and information obtained from an appropiate alignment between the sequences considered. A
model for each phase can then be locally produced. The model of the whole manufacturing process is obtained
from the concatenation of the models of the different phases. This paper presents the application of this
method to model STMicroelectronics’ manufacturing processes. STMicroelectronics’ interest in modeling its
manufacturing processes is based on the necessity to detect the discrepancies between the real processes and
experts’ definitions of them.
1 INTRODUCTION
1
Modeling manufacturing processes for the construc-
tion of complex objects like electronic chips is crucial
for maximizing productivity. The methods and the
algorithms developed in the Process Mining domain
aims at modeling such manufacturing processes with
graphs of manufacturing steps (treatments, operations
or tasks) from the timed messages contained in the
database (Cook and Wolf, 1998). The proposed al-
gorithms generally generate complex models that are
difficult to read and interpret when the process con-
tains hundred of steps.
This paper proposes a modeling method and the
corresponding algorithms to model manufacturing
processes having hundreds of steps. The proposed
method is based on cutting the sequences in subse-
quences called process phases. The way of cutting
1
This work has been made possible thanks to the finan-
cial support of STMicroelectronics, Convention 642/2008.
the sequences is based on information obtained from
an alignment between them. However, finding an ap-
propiate sequence alignment is not a simple task.
The section 2 resumes the state of art on the pro-
cess mining area and it introduces some ideas about
sequence alignment. Section 3 defines the notions of
class of equivalence and process phase that we pro-
pose and describes the algorithms that are required
to this aim. Section 4 presents the application of the
algorithms to model STMicroelectronics’ manufac-
turing processes. These manufacturing processes are
used for creating electronics chips, micro-controllers,
etc. The resulting models will be useful to control that
the implemented process correspond to the experts’
ideas. Discrepancies found will be helpful to alarm
experts’ about possible problems in production. In
section 5 a summary of the proposed method is pre-
sented. The paper concludes in section 6 with the in-
troduction of our current works.
129
Viale P., Benayadi N., Le Goc M. and Pinaton J. (2010).
MODELING LARGE SCALE MANUFACTURING PROCESS FROM TIMED DATA - Using the TOM4L Approach and Sequence Alignment Information
for Modeling STMicroelectronics’ Production Processes.
In Proceedings of the 12th International Conference on Enterprise Information Systems - Artificial Intelligence and Decision Support Systems, pages
129-138
DOI: 10.5220/0002971801290138
Copyright
c
 SciTePress

2 STATE OF ART
2.1 Process Mining Area
In the Process Mining framework, a series of mes-
sages is considered as an ordered set of events from
where a process model can be inferred and repre-
sented in some formalism (workflows, state charts or
Petri nets for examples) (van der Aalst and Weijters,
2004). One of the first algorithm was proposed in
(Agrawal et al., 1998). The algorithm aims at find-
ing workflow graphs from a set of series of events
contained in a workflow log. An event represents the
start time of a task. To avoid the problem of poten-
tial cycles (i.e. repeated events in a series), the algo-
rithm first renames the repeated labels of task before
enumerating the binary dependency relations between
the tasks. This set of relations is then reduced with the
use of the transitivity property of the binary relations.
Labels are again renamed to merge the tasks, making
possible the introduction of cycles in the model. Dif-
ficulties arise with this approach when (i) the tasks are
statistically independent and (ii) the number of tasks
is large (Agrawal et al., 1998). Nevertheless, Pinter
(Pinter and Golani, 2004) extends this algorithm no-
tably with the introduction of events marking the end
of the tasks. Similar issues in the context of software
engineering processes are investigated in (Cook and
Wolf, 1998) where the aim is to build a finite state
machine from the set of the most frequent event pat-
terns mined in a given log. In particular, the Markov
algorithm is based on a two order Markov chain that
is converted in states and state transitions. Cook and
Wolf (Cook and Wolf, 2004) extend this method to
concurrent processes and uses a first order Markov
chain for this aim. The difficulties come from the
pruning of the finite state machine to obtain a mini-
mal model and the sensibility of pruning metrics to
the ”noise” (van der Aalst and Weijters, 2004). Aalst
(van der Aalst et al., 2004) defines the class of process
that can be modeled with the α-algorithm but this al-
gorithm requires the series of events in the log to be
noise-free and complete.
There is a consensus to consider that finite state ma-
chines are difficult to understand and to validate. And
most of the proposed methods have difficulties when
(i) the process contains a lot of steps, (ii) the se-
ries in the log induce potential cycles in the models
and (iii) the sequences are not noise-free and com-
plete. The TOM4L Approach (Timed Observations
Mined for Learning, previously called Stochastic Ap-
proach Framework) (Le Goc et al., 2005) for discov-
ering temporal knowledge from timed observations
provides a general framework for modeling dynamic
processes that is based on a markovian representation
but uses abstract chronicle models (Ghallab, 1996) in-
stead of finite state machines. This framework consid-
ers that the timed messages of a series are written in
a database by a program, called a monitoring cogni-
tive agent MCA, that monitors a production process
Pr. A timed message is represented with an occur-
rence of a discrete event class C
i
= {e
i
} that is an
arbitrary set of discrete event e
i
= (x
i
, δ
i
), where δ
i
is one of the discrete value of the variable x
i
. When
the variable x
i
is not known, an abstract variable φ
i
is used to define the discrete event e
i
= (φ
i
, δ
i
) cor-
responding to the constant δ
i
. A discrete event class
is often a singleton because in that case, two discrete
event classes C
i
= {(x
i
, δ
i
)} and C
j
= {(x
j
, δ
j
)} are
only linked with the variables x
i
and x
j
when the con-
stants δ
i
and δ
j
are independent (Le Goc, 2006). This
condition is only concerned with the programs the
MCA is made with. A sequence of discrete event
class occurrences is then considered as the observ-
able manifestation of a series of state transitions in
a timed stochastic automaton representing the cou-
ple (Pr, MCA). The BJT4G algorithm represents a
set of sequences of discrete event class occurrences
with a one order Markov chain and uses an abduc-
tive reasoning to identify the set of the most proba-
ble timed sequential binary relations between discrete
event classes leading to a given class. A timed se-
quential binary relation R(C
i
,C
j
, [τ
−
i j
, τ
+
i j
]) is an ori-
ented relation between two discrete event classes C
i
and C
j
that is timed constrained with the interval
[τ
−
i j
, τ
+
i j
]. [τ
−
i, j
, τ
+
i, j
] is the time interval for observing an
occurrence of the C
j
class after an occurrence of the
C
i
class. The set of timed sequential binary relation
is an abstract chronicles model where the nodes are
discrete event classes and the links are timed sequen-
tial binary relations. This paper proposes to tackle the
two main problems of the Process Mining approaches
with the extension of the TOM4L Approach. The
first ideas of this approach has been presented in (Be-
nayadi et al., 2008).
2.2 Sequence Alignment
Before introducing the extension to the TOM4L Ap-
proach, it is necessary to introduce some ideas about
sequence alignment. These ideas are necessary to
understand the steps proposed in the algorithms for
modeling large scale manufacturing processes.
A sequence alignment consists in a way of ar-
ranging sequences to identify regions of similarity
between them. Aligned sequences are usually rep-
resented as rows within a matrix. Gaps (’-’) are in-
serted between the residues so that identical or simi-
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
130

lar residues are aligned in successive columns. In our
problem, the residues are the discret event class oc-
currences.
One of the first issue that arise when compar-
ing sequences concerns the estimation of substitution
costs. These substitution costs provide useful infor-
mation that leads the algorithms to align or not the
residues of the sequences considered. The scores for
aligning the different characters in the alphabet Σ are
obtained from a matrix S = [s
x,y
]
x∈Σ,y∈Σ
, called simi-
larity matrix (it is also called substitution matrix). The
value s
x,y
represents the similarity between the ele-
ments of the pair (x, y), x ∈ Σ, y ∈ Σ. In biology, there
exists some well-known substitution matrices. How-
ever, this problem has also been encountered in many
other areas, for example, in social sciences where
there are no well known similarity matrices precal-
culated. The problem in social science is to compare
chronological sequences of various kind (e.g. profes-
sional or familial statuses) where there is no equiva-
lent to such a strong theoretical and empirical frame-
work like evolutionary theory. Thus the relationship
between the symbols constituting sequences of social
events remain at least partly uncertain. The ideas from
social science field can guide us towards to find a
strategy to build similarity matrices for any kind of
sequences. The idea is to find a way to construct the
similarity matrix S for any kind of sequence, deriving
costs empirically. An adaptation of the algorithm for
calculating substitution costs iteratively is necessary
(Gauthier et al., 2008).
3 EXTENSION OF THE TOM4L
APPROACH FOR PROCESS
MINING
3.1 Motivation
Let us take an example to illustrate the proposed ex-
tensions with a manufacturing process having a set
S = {A, B,C, D, E, F} of 6 manufacturing steps. Sup-
pose the supervision system records the execution of a
step with a message X(t
k
) denoting the time t
k
of the
beginning of the execution of the step X. The three
series of messages of table 1 are represented with the
abstract chronicle model of figure 1. In this model, if
nodes labeled with A denote the same manufacturing
step, then the nodes can be confused, introducing a
cycle in the model. The same reasoning can be done
over the other nodes, making the model difficult to
read and to understand.
This repetition of manufacturing steps can be due
Table 1: Three series of event.
A(t
1
)B(t
2
)F(t
3
)B(t
4
)E(t
5
)D(t
6
)C(t
7
)A(t
8
)E(t
9
)B(t
10
)
A(t
11
)B(t
12
)E(t
13
)C(t
14
)D(t
15
)A(t
16
)E(t
17
)B(t
18
)
A(t
19
)B(t
20
)E(t
21
)C(t
22
)D(t
23
)A(t
24
)E(t
25
)B(t
26
)
Figure 1: Model for the three Sequences.
to a situation that arrives frequently during the exe-
cution of a manufacturing process. When an object
is being manufactured, the object goes from one ma-
chine to another for making all the necessary treat-
ments on it. Nevertheless, usual controls in pro-
duction sometimes show that certain objects did not
achieved the expected characteristics. Some actions
(special actions) has to be done to correct the prob-
lem. These actions usually consist on performing spe-
cial treatments and/or the repetition of tasks.
This is the reason why we need to align the differ-
ent process execution sequences to identify equivalent
treatments over the different objects being produced
in each execution.
Given a set Ω = {ω
i
}
i={1,...,n}
of sequences ob-
tained from the execution of the same manufacturing
process, we need a ’good’ sequence alignment be-
tween them, SA(Ω) . By ’good’ we mean an align-
ment that aligns similar treatments made on the dif-
ferent objects on the same column and special tasks
(task performed to correct errors) with gaps (’-’).
Two possible ’good’ alignment for the sequences
shown in Table 1 are proposed in Table 2.
Suppose now that each of the three sequences are
cut when a label is aligned with exactly the same one
in all sequences and this alignment appears two times.
The model of the first part of the sequences will be
similar to the one of figure 1 but without the path
A − E − B at the end of the model. This fact moti-
vates the notion of process phase proposed in this pa-
per. But this notion is not sufficient to solve the cycles
that are introduced with the steps C and D. We con-
sider that this problem is due to the fact that the three
series of events provide no information about the or-
der of the steps C and D. Consequently, any solution
of this problem must take into account some a priori
knowledge about the process which we want to avoid
it. The notion of potential cycle is then defined to de-
tect this kind of situation to be able to make further
investigations (i.e. finding new series or discussing
MODELING LARGE SCALE MANUFACTURING PROCESS FROM TIMED DATA - Using the TOM4L Approach and
Sequence Alignment Information for Modeling STMicroelectronics' Production Processes
131

Table 2: Two Sequence Alignments proposed for sequences on Table 1.
Possible Sequence Alignments
SA
1
=


A(t
1
) B(t
2
) F(t
3
) B(t
4
) E(t
5
) D(t
6
) C(t
7
) − A(t
8
) E(t
9
) B(t
10
)
A(t
11
) B(t
12
) − − E(t
13
) − C(t
14
) D(t
15
) A(t
16
) E(t
17
) B(t
18
)
A(t
19
) B(t
20
) − − E(t
21
) − C(t
22
) D(t
23
) A(t
24
) E(t
25
) B(t
26
)


SA
2
=


A(t
1
) B(t
2
) F(t
3
) B(t
4
) E(t
5
) − D(t
6
) C(t
7
) A(t
8
) E(t
9
) B(t
10
)
A(t
11
) B(t
12
) − − E(t
13
) C(t
14
) D(t
15
) − A(t
16
) E(t
17
) B(t
18
)
A(t
19
) B(t
20
) − − E(t
21
) C(t
22
) D(t
23
) − A(t
24
) E(t
25
) B(t
26
)


with experts for examples).
To illustrate the notion of class of equivalence, let
us take the Edit activity of the ”writing a scientific pa-
per” process that can be made by different students
and professors. The Edit activities can then be la-
beled differently according to the performer with a set
of classes of the form: C = {C
E1
= {(s
1
, δ
1
)},C
E2
=
{(s
2
, δ
2
)}, . . .}, where the variables s
i
and p
i
denotes
respectively students and professors. In this case,
the resulting model of the process will be complex
without necessity. One of the interesting features of
the TOM4L Approach is the notion of discrete event
class. This notion can be used to define abstract
classes of the form C
φ
i
= {(φ
i
, δ
1
), . . . , (φ
i
, δ
n
)} where
φ
i
denotes an abstract variable and the set {δ
j
}, j =
1. . . n, is an arbitrary set of constants. This property
allows defining classes of equivalence that simplifies
a process model. For example, an abstract class C
φ
i
be defined as an equivalent class of the set of classes
C of the ”writing a scientific paper” process. Doing
this way allows constituting a set of sequences com-
ing from different students and professors.
3.2 Class of Equivalence
By definition, a large scale process consist on a lot
of steps. Some of these steps differs only with some
characteristics but realizes similar treatments.
Definition 1 . Given a model M =
{R(C
i
,C
j
, [τ
−
i j
, τ
+
i j
])} build with a set Ω = {ω
i
}
of discrete event class occurrences ω
i
, a class
C
φ
i
= {(φ
i
, δ
1
), (φ
i
, δ
2
), . . . , (φ
i
, δ
n
)} is an equiv-
alence class of a sub set of classes C = {C
j
},
j = 1 . . . n, C
j
= {(x
j
, δ
j
)}, of the set of classes C
M
of
a model M iff:
∀C
a
,C
b
∈ C
∀C
k
∈ C
M
,
(∃R(C
k
,C
a
, [τ
−
ka
, τ
+
ka
]) ∈ M ∧ ∃R(C
k
,C
b
, [τ
−
kb
, τ
+
kb
]) ∈ M)
∧ (1)
∀C
r
∈ C
M
,
(∃R(C
a
,C
r
, [τ
−
ar
, τ
+
ar
]) ∈ M ∧ ∃R(C
b
,C
r
, [τ
−
br
, τ
+
br
]) ∈ M)
This definition means that every classes C
j
of
the subset C ⊆ C
M
are linked with the same classes
in M. When this condition is verified, each oc-
currences C
j
(t
s
) of the classes C
j
in the sequences
ω
i
of Ω can be rewritten as occurrences C
φ
i
(t
s
)
of the equivalence class C
φ
i
. The abstract vari-
able φ
i
has no a priori meaning: φ
i
can be substi-
tuted with the corresponding concrete variable x
i
in
any occurrences C
φ
i
(t
s
). Consequently, the set of
uphill relations {R(C
i
,C
j
, [τ
−
i j
, τ
+
i j
])} of M will be-
come {R(C
i
,C
φ
i
, [τ
−
iφ
i
, τ
+
iφ
i
])} and the set of down-
hill relations {R(C
j
,C
k
, [τ
−
jk
, τ
+
jk
])} of M will become
{R(C
φ
i
,C
k
, [τ
−
φ
i
k
, τ
+
φ
i
k
])}. In practice, an equivalence
class can be used to represent related discrete event
classes. In the application presented in the next sec-
tion, a discrete event class represents a set of treat-
ments that can be made on an object using a particular
machine. Equivalence classes are then used to repre-
sent this set of treatments made by different machines:
in that case, the machines are equivalents because the
same set of treatments can be done on each of the ma-
chines.
Given a set of sequences Ω = {ω
i
}
i={1,...,n}
, the
algorithm for defining equivalence classes find all the
equivalence classes and rewrite the corresponding oc-
currences in each sequence ω
i
(Algorithm 1):
1. Build a model M given a set of sequences Ω =
{ω
i
}
i={1,...,n}
.
2. Find all the subset of classes C verifying the equa-
tion 1.
3. For all the subsets C.
• Create an equivalence class C
φ
i
.
• For all C
j
∈C, rewrite all the occurrences C
j
(t
s
)
in all the sequences ω
i
∈ Ω with the rewriting
rule: C
j
(t
s
) ≡ C
φ
i
(t
s
).
4. Build a new model M
0
with Ω.
3.3 Process Phase
The information contained in a series of manufactur-
ing messages is concerned with both the state of the
manufactured object and the manufacturing process
that makes evolving this state from an initial state up
to a final state. But generally, the state of the manufac-
tured object is not provided with the messages. So we
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
132

propose to capture indirectly this dimension with the
notion of Process Phase. However, before introduc-
ing this new concept, we must define formally what is
called a Sequence Alignment.
3.3.1 Sequence Alignment
A sequence alignment consists in a way of arranging
sequences to identify regions of similarity between
them. Aligned sequences are usually represented
as rows within a matrix M = [m
i, j
]
i∈{1,...,n}, j∈{1,...,r}
.
Gaps (’-’) are inserted between the residues so that
identical or similar residues are aligned in successive
columns.
Definition 2 . Given a model M =
{R(C
i
,C
j
, [τ
−
i j
, τ
+
i j
])} build with a set Ω = {ω
i
}
of discrete event class occurrences. A sequence
alignment SA between all sequences ω
i
∈ Ω is
defined as follows:
SA(Ω) = {M
n×r
|
∀ω
j
∈ Ω, r ≥ card(ω
j
) ∧
∀m
i j
∈ M
n×r
, m
i j
∈ C
M
∪ {
0
−
0
} ∧
∀m
i j
, m
i( j+1)
∈ M
n×r
, (2)
(m
i j
= C
j
(t
k
),C
j
(t
k
) ∈ ω
i
∧
m
i( j+1)
= C
l
(t
x
),C
l
(t
x
) ∈ ω
i
∧
t
x
> t
k
)}
where:
- card(s) is the length of sequence s.
There are many possible alignments between n
sequences. There exists many algorithms for creat-
ing sequence alignments based on different objectives
and strategies (Thompson et al., 1994; Notredame
et al., 2000; Needleman and Wunsch, 1970; Smith
and Waterman, 1981). However, it is necessary to
provide a similarity matrix S to these algorithms so
that they are able to calculate when to align or not
residues of the different sequences. If we use the same
alignment algorithm over the same set of sequences
with different similarity matrices the resulting align-
ments will be probably not the same. So, it is very im-
portant to use a similarity matrix that agrees with the
semantics of the sequences treated. We will illustrate
this problem in section 4, over STMicroelectronics’
manufacturing process sequences.
Given a set of sequences Ω = {ω
i
}
i={1,...,n}
and a
sequence alignment SA(Ω), we propose an algorithm
for renaming classes.This algorithm traverses all se-
quences and renames a class if in the alignment it is
aligned with classes different from itself or with gaps
(Algorithm 2):
• ∀ω
i
∈ Ω, ∀C
j
(t
k
) ∈ ω
i
do:
– Rename the occurrence C
j
(t
k
) when:
- ∃C
i
(t
s
) ∈ w
m
, w
m
∈ Ω,C
j
(t
k
) is aligned with
C
i
(t
s
) in SA(Ω) and C
i
6= C
j
; or
- C
j
(t
k
) is aligned with a gap (’-’) in SA(Ω).
In Table 3 we will show the corresponding series
from Table 1 after applying Algorithm 2 on them,
considering sequence alignment SA
1
.
3.3.2 Process Phase Concept
As it was said before, the concept of process phase
will be used to capturate the different stages that an
object must go through in the manufacturing process
to achieve the final expected state. For this task we
need to count with a ’good’ sequence alignment of the
sequences that we use to build the model. The reason
is that this alignment provides a guideline to distin-
guish normal treatments from special tasks performed
in particular executions of the process. Aligned tasks
are supposed to be regular tasks whereas not aligned
tasks are not.
Definition 3 . Given a set of sequences
Ω = {ω
i
}
i={1,...,n}
and a sequence alignment
SA(Ω), a process phase of the model M con-
structed using Algorithm 2 is a submodel
M
0
= {R(C
i
,C
j
, [τ
−
i j
, τ
+
i j
])|C
i
,C
j
∈ C
M
0
} ⊆ M, so
that there is no path P = {R(C
i
,C
i+1
,
[τ
−
ii+1
, τ
+
ii+1
])} ∈ M
0
, i = 1 . . . n, where:
∀ j, k ∈ N, 1 ≤ j < k ≤ n,C
j
= C
k
(3)
Algorithm 3 aims at cutting a set Ω =
{ω
i
}
i={1,...,n}
of sequences in subsequences ω
i
k
that
respects the equation 3 (i.e. ω
i
k
does not contain two
occurrences of the same class):
1. ∀ω
i
∈ Ω do
• Remove ω
i
from Ω.
• Cut up ω
i
in a set Ω
i
= {ω
i
k
} of sub sequences
ω
i
k
verifying the equation 3.
2. ∀ω
i
k
∈ Ω
i
do
• Add an occurrence of the C
0
and C
1
classes at
the beginning and the end of ω
i
k
.
3. Ω =
S
Ω
i
.
An occurrence of an abstract start class C
0
and
an occurrence of an abstract final class C
1
are
added at the beginning and the end of each sub
sequences ω
i
k
so that the BJT 4G algorithm auto-
matically identifies the process phases. For exam-
ple, when applying the algorithm 3 on the three
sequences of Table 1, the BJT 4G algorithm will
find two process phases. The second process phase
MODELING LARGE SCALE MANUFACTURING PROCESS FROM TIMED DATA - Using the TOM4L Approach and
Sequence Alignment Information for Modeling STMicroelectronics' Production Processes
133

Table 3: Series of event after renaming with Algorithm 2.
A(t
1
) B(t
2
) F
1,3
(t
3
) B
1,4
(t
4
) E(t
5
) D
1,6
(t
6
) C(t
7
) A(t
8
) E(t
9
) B(t
10
)
A(t
11
) B(t
12
) E(t
13
) C(t
14
) D
2,15
(t
15
) A(t
16
) E(t
17
) B(t
18
)
A(t
19
) B(t
20
) E(t
21
) C(t
22
) D
3,23
(t
23
) A(t
24
) E(t
25
) B(t
26
)
will be: { R(C
0
,C
A
, [τ
−
0A
, τ
+
0A
]) , R(C
A
,C
E
, [τ
−
AE
, τ
+
AE
]),
R(C
E
,C
B
, [τ
−
EB
, τ
+
EB
]), R(C
B
,C
1
, [τ
−
B1
, τ
+
B1
]) }.
It can be easily deduced from the definition of pro-
cess phase that process phases are dependent on the
sequence alignment chosen. It is necessary to count
with a ’good’ sequence alignment for being able to
correctly identify the different stages in the process.
3.4 Potential Cycles
When looking the model of figure 1, it is clear
that the classes C and D introduce a cycle. Cycles
present a strong problem of interpretation, making
hard to understand the resulting models. This explains
why there is a lot of works aiming at avoiding cy-
cles in process models (cf. (Cook and Wolf, 2004),
(Schimm, 2004) (van der Aalst et al., 2004), (Pin-
ter and Golani, 2004), (Weijters and van der Aalst,
2003) or (Agrawal et al., 1998) for examples). But
these works make assumptions about the process or
impose constraints about the constitution of the se-
quences. In all the case, this consists in having some
a priori knowledge about the process to be modeled
or the set of programs that write the messages in the
process data base.
The aim of the TOM4L Approach is to provide
models of sequences without any a priori knowledge
about the process and the set of programs that have
generated the occurrences. One difficulty is that cy-
cles often appear when mining a process because of
the transitivity property of the sequential binary rela-
tions.
Property 1 . The timed sequential binary relations
R(C
i
,C
j
, [τ
−
i j
, τ
+
i j
]) of a given abstract chronicle model
M = {R(C
i
,C
j
, [τ
−
i j
, τ
+
i j
])} are transitives.
∀R(C
i
,C
j
, [τ
−
i j
, τ
+
i j
]) ∈ M ∧ ∀R(C
j
,C
k
, [τ
−
jk
, τ
+
jk
]) ∈ M
R(C
i
,C
j
, [τ
−
i j
, τ
+
i j
]) ∧ R(C
j
,C
k
, [τ
−
j,k
, τ
+
j,k
])
⇒ ∃R
T
(C
i
,C
k
, [τ
−
ik
, τ
+
ik
]) (4)
Definition 4 . Given a process model M, two discrete
event classes C
i
and C
j
are not ordered when:
M ` R
T
(C
i
,C
j
, [τ
−
i j
, τ
+
i j
]) ∧ M ` R
T
(C
j
,C
i
, [τ
−
ji
, τ
+
ji
]) (5)
Two classes C
i
and C
j
that can not be ordered in a
model will be denoted C
i
kC
j
≡ C
j
kC
i
.
For examples the three sequences of the Table 1
do not provide any order between the classes C
C
and
C
D
(Figure 1). Consequently: C
C
kC
D
≡ C
C
kC
D
.
Property 2 . The set of discrete event classes C
k
=
{C
1
,C
2
, . . . ,C
n
} can not be ordered when:
∀C
i
∈ C
k
, ∀C
j
∈ C
k
,C
i
kC
j
. (6)
In the theory of graphs, the classes of a set C
k
are strongly connected components. The algorithm
4 aims at detecting a potential cycle (i.e. a set C
k
is
defined):
1. Build a process model M from Ω with the BJT 4G
algorithm.
2. Build the set Ck = {C
k
i
} of the sets C
k
i
of classes
without order with the equation 5
3. ∀C
k
i
∈ Ck do
• Remove the relations R(C
i
,C
j
, [τ
−
i j
, τ
+
i j
]) of M
where C
i
∈ C
k
i
or C
j
∈ C
k
i
.
• Generate all the pathes P = {P
k
} with P
k
=
{R(C
i
,C
i+1
, [τ
−
ii+1
, τ
+
ii+1
])} where C
i
∈ C
k
i
and
C
i+1
∈ C
k
i
• Insert the relations of the pathes P in M.
To avoid the adding of a priori knowledge about the
process or the programs, the algorithm 4 computes
all the paths linking the classes in C
k
(cf. model of
Figure 1 with the classes C and D). It is clear that if
Card(C
k
) = n, there is n! possible paths. But it is a
simple way to put the emphasis on potential cycles.
3.5 Modeling a Large Scale Process
The algorithm 5 aims at modeling a large scale man-
ufacturing process. It simply uses the four algorithms
provided in the preceding subsections. Given a set
of sequences Ω = {ω
i
}
i={1,...,n}
and a sequence align-
ment SA(Ω), the algorithm 5 finds a process model M
with the BJT 4G algorithm:
1. Rewrite the sequences of Ω with the algorithm 1.
2. Rewrite the sequences of Ω with the algorithm 2
using information from SA(Ω).
3. Produce the sets Ω
k
of subsequences ω
i
k
with the
algorithm 3.
4. ∀Ω
k
do
• Build a process model M
k
of the phase k with
the algorithm 4.
5. M =
S
M
k
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
134

Applied to the sequences of the Table 1, this al-
gorithm provides the model of the Figure 1. This al-
gorithm has also been used to model the wafer manu-
facturing process of the Rousset (France) plant of the
STMicroelectronics company.
4 APPLICATION
The aim of STMicroelectronics Company is to im-
prove the control of the wafer manufacturing pro-
cesses through the definition of human scale process
models and a better knowledge of the timed con-
straints between the different steps of manufacturing.
A ”wafer” is a silicon plate used for the construc-
tion of STMicroelectronics’ products. A wafer manu-
facturing process is a series of elementary treatments
called ”recipes” that are executed on machines called
”equipments”. An ”operation” is a particular serie
of recipes and each recipe is associated with differ-
ent equipments, those that are qualified for perfom-
ing the treatment. A complete series of operations is
called ”manufacturing route”. The STMicroelectron-
ics’ plant situated in the south of France, in Rousset,
counts with more than 10.000 different recipes, each
manufacturing route is composed of about 400 oper-
ations and there are actually more than 300 equip-
ments in the plant. The supervision system of the
wafer manufacturing process describes a manufac-
turing route with messages providing the name of a
recipe, the machine on which the recipe is executed,
the corresponding operation and the start and finish
times of the recipe.
For validating the approach presented in this
paper, a set Ω containing 5 sequences ω
i
, i =
{1, . . . , 5}, has been extracted from STMicroelectron-
ics’ databases. These sequences contain data from
real production of the Company. For the construc-
tion of this example we considered an extract of each
of these 5 sequences ω
i
, i = {1, . . . , 5}. Only the 200
first executed recipes were used.
The Algorithm 5 has been applied at the equip-
ment level so that a process model M represents a
manufacturing route by a serie of equipments. Even
though we worked with extracts of real routes, we
found a large volume of data. In the example con-
structed, 127 discret event classes have been found.
A class is defined with a singleton C
i
= {(φ
i
, i)}
where the constant i is a natural number in the inter-
val [1000, . . . , 1126]. Each of these classes represent
a particular equipment in STMicroelectronics’ plant.
We will illustrate the application of the approach
proposed in this paper showing how it works over two
subsequences of sequences ω
1
and ω
2
used for the
example construction. These two subsequences can
be seen in Figure 2.
Figure 2: Subsequence of ω
1
(up) and subsequence of ω
2
(down).
During the example construction, 67 differ-
ent equivalent classes have been found. The
equivalent classes created using Algorithm
1 are singletons of the form C
j
= {(φ
j
, j)}
with j ∈ [6000, 6066]. Consider the equiva-
lent class C
6008
= {(φ
6008
, 6008)} contains the
discret event classes {C
1031
,C
1032
,C
1033
} and that
{C
1010
,C
1011
,C
1012
} ⊆ C
6009
, {C
1050
,C
1051
,C
1052
} ⊆
C
6031
, {C
1040
,C
1041
} ⊆ C
6040
, {C
1020
} ⊆ C
6042
,
{C
1060
,C
1061
} ⊆ C
6046
,{C
1080
,C
1081
} ⊆ C
6056
,
{C
1070
,C
1071
} ⊆ C
6065
. The algorithm 1 rewrites
the two subsequences of Figure 2 and produces the
subsequences of Figure 3.
Figure 3: Subsequences of ω
1
and ω
2
rewritten with Algo-
rithm 1.
Suppose now that we construct alignments be-
tween the two subsequences of ω
1
and ω
2
, using an
optimal algorithm (Needleman and Wunsch, 1970)
and two different similarity matrices S
1
and S
2
shown
in table 4. The main difference between these two
matrices is that S
2
penalizes the alignment of differ-
ent residues wherereas S
1
does not. A ’-1’ penalty is
used for the introduction of gaps.
The alignment corresponding to the two subse-
quences using the similarity matrix S
1
is shown in
Figure 4. The alignment for similarity matrix S
2
can
be seen in Figure 5.
Figure 4: Subsequences of ω
1
and ω
2
aligned using simi-
larity matrix S
1
.
After analysing the alignment with STMicroelec-
tronics’ experts we could corroborate that only the
alignment constructed using matrix S
2
respects the se-
mantics of the sequences. This tiny example shows
MODELING LARGE SCALE MANUFACTURING PROCESS FROM TIMED DATA - Using the TOM4L Approach and
Sequence Alignment Information for Modeling STMicroelectronics' Production Processes
135

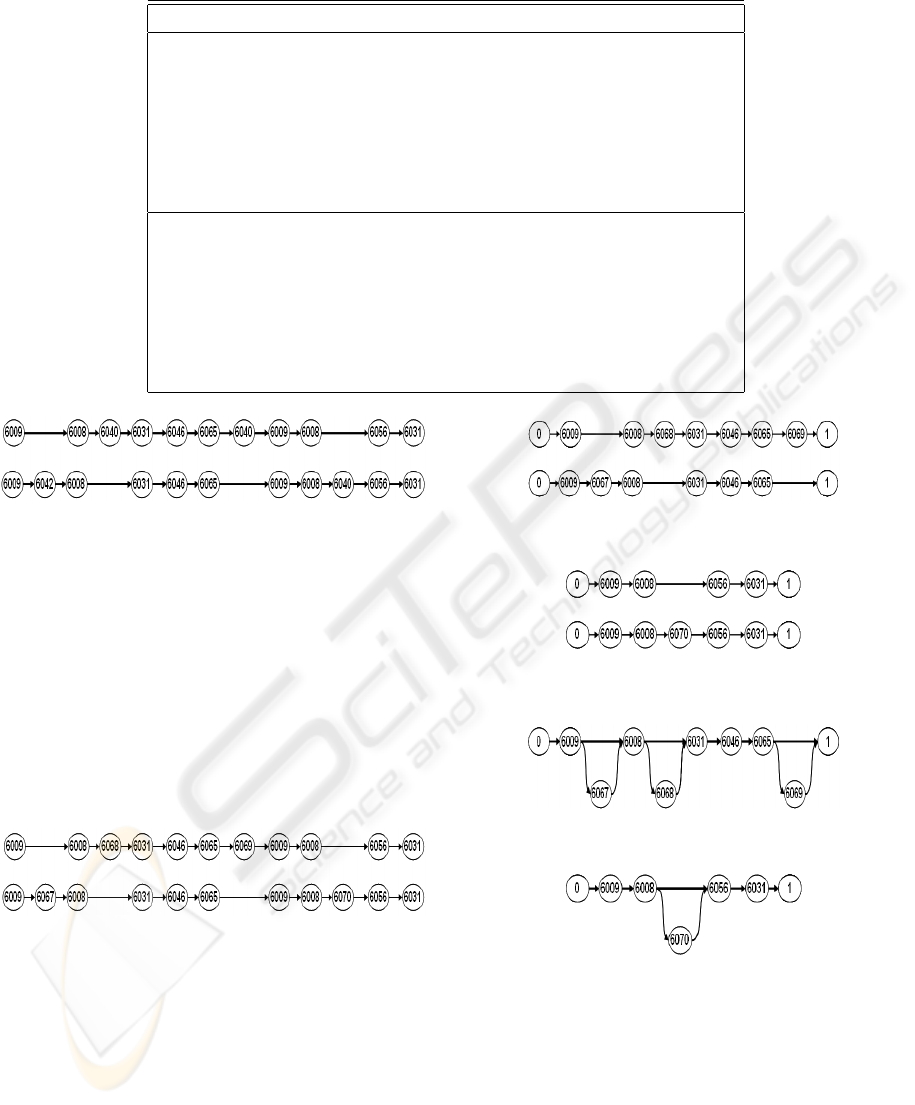
Table 4: Two possible similarity matrices for residues of subsequences of ω
1
and ω
2
considered.
Similarity matrices
S
1
=












− 6008 6009 6031 6040 6042 6046 6056 6065
6008 1 0 0 0 0 0 0 0
6009 0 1 0 0 0 0 0 0
6031 0 0 1 0 0 0 0 0
6040 0 0 0 1 0 0 0 0
6042 0 0 0 0 1 0 0 0
6046 0 0 0 0 0 1 0 0
6056 0 0 0 0 0 0 1 0
6065 0 0 0 0 0 0 0 1












S
2
=












− 6008 6009 6031 6040 6042 6046 6056 6065
6008 1 −1 −1 −1 −1 −1 −1 −1
6009 −1 1 −1 −1 −1 −1 −1 −1
6031 −1 −1 1 −1 −1 −1 −1 −1
6040 −1 −1 −1 1 −1 −1 −1 −1
6042 −1 −1 −1 −1 1 −1 −1 −1
6046 −1 −1 −1 −1 −1 1 −1 −1
6056 −1 −1 −1 −1 −1 −1 1 −1
6065 −1 −1 −1 −1 −1 −1 −1 1












Figure 5: Subsequences of ω
1
and ω
2
aligned using simi-
larity matrix S
2
.
the importance of choosing the right matrix to calcu-
late the alignment between all sequences considered.
An error in this step will introduce a problem that will
be carried over the following steps. Working with a
wrong sequence alignment will probably conduce to
errors when cutting sequences in process phases.
After applying Algorithm 2 for renaming classes
according to the alignment shown in Figure 5, the sub-
sequences of ω
1
and ω
2
are rewritten as it is shown in
Figure 6.
Figure 6: Subsequences of ω
1
and ω
2
rewritten using Algo-
rithm 2.
Algorithm 3 finds two process phases (i and i +
1) for the subsequence considered of ω
1
and for the
subsequence considered of ω
2
. Process phase i can
be seen in Figure 7 and process phase i + 1 is shown
in Figure 8.
Using Algorithm 4 over the phases found, the cor-
responding models were constructed. Following the
two subsequences used for illustrating the approach,
we construct the models shown in Figures 9 and 10.
During the construction of the hole example
Figure 7: ω
i
1
(up) and ω
i
2
(down).
Figure 8: ω
i+1
1
(up) and ω
i+1
2
(down).
Figure 9: Model for phase i obtained from ω
i
1
and ω
i
2
.
Figure 10: Model for phase i + 1 obtained from ω
i+1
1
and
ω
i+1
2
.
model, 19 process phases were found. The resulting
model contains a total of 302 nodes.
In Figure 11 the resulting model constructed for
the 5th phase found is shown. The volume of data in
this small example is large even though we worked
with extracts of manufacturing routes. The model ob-
tained using this method is, however, simple and easy
to understand. The resulting model has already been
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
136

Figure 11: Phase 5 of the model.
validated by STMicroelectronics’ experts.
The next step is to build a model of for com-
plete sequences and for bigger sets (more than 5 se-
quences). Afterwards, it would be valuable to con-
struct models for other levels of granularity (level of
operations or recipe level are some options).
5 CONCLUSIONS
This paper presents the TOM4L Approach for mod-
eling manufacturing processes from timed data con-
tained in a supervision system database. One of the
interesting features of this approach is the notion of
discrete event class. This notion is used to define a
process phase concept and discrete event classes of
equivalence that are required for large scale manu-
facturing processes. The definition of these concepts
leads to a global algorithm that has been applied to
modeling STMicroelectronics’ (Rousset) manufactur-
ing processes. This concrete application shows the
operational flavor of the extensions of the TOM4L
Approach. The importance of calculating a simi-
larity matrix that corresponds to sequence semantics
has also been shown in the applicative section. The
construction of these models will be a valuable tool
for STMicroelectronics to control production and to
alarm experts when the real activity of the Company
does not follow their theoretical definitions.
6 CURRENT WORKS
Current works are devoted to find an analogy of the
work presented in (Gauthier et al., 2008), works done
on the social science field. Our idea is to find a way
to calculate the similarity values between different
events classes in any kind of sequence, without in-
troducing experts knowledge about their contents.
REFERENCES
Agrawal, R., Gunopulos, D., and Leymann, F. (1998). Min-
ing process models from workflow logs. In Sixth In-
ternational Conference on Extending Database Tech-
nology, pages 469–483.
Benayadi, N., Le Goc, M., and Bouch
´
e, P. (2008). Using the
stochastic approach framework to model large scale
manufacturing processes. Proceedings of the 3rd In-
ternational Conference on Software and Data Tech-
nologies (ICSoft 2008).
Cook, E. J. and Wolf, A. L. (1998). Discovering models
of software processes from event-based data. ACM
Transactions on Software Engineering and Methodol-
ogy, 7:215–249.
Cook, E. J. and Wolf, A. L. (2004). Event-based detec-
tion of concurrency. In Proceedings of the 6th ACM
SIGSOFT international symposium on Foundations of
software engineering, volume 53, pages 35–45.
Gauthier, J. A., Widmer, E. D., Bucher, P., and Notredame,
C. (2008). How much does it cost? optimization of
costs in sequence analysis of social science data. So-
ciological Methods and Research.
Ghallab, M. (1996). On chronicles: Representation, on-line
recognition and learning. Proc. Principles of Knowl-
edge Representation and Reasoning, Aiello, Doyle
and Shapiro (Eds.) Morgan-Kauffman, pages 597–
606.
Le Goc, M. (2006). Notion d’observation pour le diagnostic
des processus dynamiques: Application
`
a Sachem et
`
a la d
´
ecouverte de connaissances temporelles. Hdr,
Facult
´
e des Sciences et Techniques de Saint J
´
er
ˆ
ome.
Le Goc, M., Bouch
´
e, P., and Giambiasi, N. (2005). Stochas-
tic modeling of continuous time discrete event se-
MODELING LARGE SCALE MANUFACTURING PROCESS FROM TIMED DATA - Using the TOM4L Approach and
Sequence Alignment Information for Modeling STMicroelectronics' Production Processes
137

quence for diagnosis. 16th International Workshop on
Principles of Diagnosis (DX’05) , California, USA.
Needleman, S. B. and Wunsch, C. D. (1970). A general
method applicable to the search of similarities in the
amino acid sequence of two proteins. J. Mol. Biol.,
48:443–453.
Notredame, C., Higgins, D. G., and Heringa, J. (2000). T-
coffee: A novel method for fast and accurate multiple
sequence alignment. J. Mol. Biol., 302:205–217.
Pinter, S. and Golani, M. (2004). Discovering workflow
models from activities’ lifespans. In Special issue:
Process/workflow mining, volume 53, pages 283–296.
Schimm, G. (2004). Mining exact models of concurrent
workflows. In Computers in Industry, volume 53(3),
pages 265–281.
Smith, T. F. and Waterman, M. S. (1981). Identification
of common molecular subsequences. J. Mol. Biol.,
147:195–197.
Thompson, J. D., Higgins, D. G., and Gibson, T. J. (1994).
Clustal w: improving the sensitivity of progres-
sive multiple sequence alignment through sequence
weighting, position-specific gap penalties and weight
matrix choice. Nucleic Acid Research, 22:4673–4680.
van der Aalst, W., Weijters, T., and Maruster, L. (2004).
Workflow mining: Discovering process models from
event logs. In IEEE Transactions on Knowledge and
Data Engineering, volume 16, pages 1128–1142.
van der Aalst, W. M. P. and Weijters, A. J. M. M. (2004).
Process mining. Special issue of Computers in Indus-
try, 53:231–244.
Weijters, A. and van der Aalst, W. (2003). Rediscovering
workflow models from event-based data using little
thumb. In Integrated Computer-Aided Engineering,
volume 10(2), pages 151–162.
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
138