
DENOISING NETWORK TOMOGRAPHY ESTIMATIONS
Muhammad H. Raza, Bill Robertson, William J. Phillips
Department of Engineering Mathematics and Internetworking, Dalhousie University, Nova Scotia, Halifax, Canada
Jacek Ilow
Department of Electrical Engineering, Dalhousie University, Nova Scotia, Halifax, Canada
Keywords:
Network tomography, Sparse code shrinkage, Error modeling, Link delays.
Abstract:
In this paper, we apply the technique of sparse shrinkage coding (SCS) to denoise the network tomography
model with errors. SCS is used in the field of image recognition for denoising of the image data and we are the
first one to apply this technique for estimating error free link delays from erroneous link delay data. To make
SCS properly adoptable in network tomography, we have made some changes in the SCS technique such as the
use of Non Negative Matrix Factorization (NNMF) instead of ICA for the purpose of estimating sparsifying
transformation. Our technique does not need the knowledge of the routing matrix which is assumed known in
conventional tomography. The estimated error free link delays are compared with the original error free link
delays based on the data obtained from a laboratory test bed. The simulation results reveal that denoising of
the tomography data has been carried out successfully by applying SCS.
1 INTRODUCTION
Computer networks have emerged as the primary
setup for communication in present global scenario.
With a broad range of applications on the networks
using diverse technologies, there is a growing need
to better understand and characterize the network dy-
namics. High quality traffic measurements are a key
to successful network management. Direct observa-
tion of the desired statistics in a network is not pos-
sible without the special cooperation of the internal
network resources. For example, routers do not main-
tain per user or per flow information, but performance
metrics such as loss or utilization statistics are avail-
able at router interfaces (Zhao et al., 2006),(Coates
and Nowak, 2001).
Cooperation to obtain internal information from
privately owned networks is almost impossible to
get. The network communication research commu-
nity has always been looking for the alternatives to
get around this problem. However, some useful pa-
rameters can be obtained from passive monitoring of
traffic or active probing of a network. The desired
statistics (that needs internal cooperation of private
networks) are then indirectly estimated from these di-
rectly measured statistics (requiring no internal co-
operation). Also, for the diverse nature of network
applications of today, the service providers need dif-
ferential measurements such as individual link perfor-
mance to avoid congestion and keep the service level
agreements (Zhao et al., 2006), (Coates and Nowak,
2001). The phenomenon of estimating desired statis-
tics indirectly from directly measured parameters is
called network tomography. The simplest model of
network tomography is represented by the following
equation,
Y = AX, (1)
linking the measured parameters matrix (Y) with the
matrix of unknown parameters (X) with dependence
on the routing matrix (A) of the network. If Y has I
rows and X has J rows, then the size of the routing
matrix (A) is I×J. The rows of A (A
i
) correspond to
paths from the sender to the receiversand the columns
(A
j
) correspond to individual links in those paths.
In reality, all the practical networks have the po-
tential of errors that should be reflected in the network
tomographic model as Y = AX+ε, where ε represents
the error in the model.
There are various sources that contribute towards
the error term (ε) such as Simple Network Manage-
ment Protocol (SNMP) operation and NetFlow mea-
surements. The heterogeneity of the network compo-
nents in terms of vendors and hardware/software plat-
67
H. Raza M., Robertson B., J. Phillips W. and Ilow J. (2010).
DENOISING NETWORK TOMOGRAPHY ESTIMATIONS.
In Proceedings of the International Conference on Data Communication Networ king and Optical Communication Systems, pages 67-72
DOI: 10.5220/0002972800670072
Copyright
c
SciTePress

forms that are used by various types of networking
technologies, is also a contributing factor toward the
error term, ε.
In this paper, we have applied SCS technique to
denoise the noisy link delay data. A key idea that
constitutes the rationale behind sparse code shrinkage
(SCS) is to use a basis that is more suitable for data at
hand. For denoising, it is required to transform data
to a sparse code, apply maximum likelihood (ML)
estimation procedure component-wise, and transform
back to the original variables. The simulation results
show that the proposed technique needs less input and
assumptions to denoise and recover almost noise free
(original) data.
The rest of the paper is organized as follows. Sec-
tion 2 briefly describes network tomography and var-
ious factors that introduce errors in tomography data.
Section 3 reviews related work. Section 4 discusses
SCS and the rationale for using SCS. Section 5 ex-
plains application of NNMF in the context of network
tomography and sparsity. Section 6 presents and dis-
cusses results to show that SCS successfully denoises
the noisy link delay data with out a priori knowledge
of routing matrix. Section 7 concludes the paper.
2 FACTORS INTRODUCING
ERRORS IN NETWORK
TOMOGRAPHY
Vardi (Vardi, 1996) was the first one to introduce the
term of network tomography for an indirect infer-
ence of desired statistics. Three categories of network
tomography problems (active, passive, and topology
identification) have been addressed in the literature.
In passive network tomography (Vardi, 1996), link
level statistics such as bit rate are passively measured
as matrix Y and origin destination (OD) flows are es-
timated as X.
In active network tomography (Castro et al.,
2004), (Coates and Nowak, 2001), unicast or mul-
ticast probes are sent from a single or multiple
source(s) to destination(s) and parameters such as
packet loss rate (PLR), delay and bandwidth are de-
termined from source destination measurements.
The key idea in most of the existing topology iden-
tification methods is to collect measurements at pairs
of receivers (Castro et al., 2004).
Simple Network Management Protocol (SNMP)
and NetFlow are the main contributors towards the
error term (ε) along with the heterogeneity of the
network components in terms of vendors and hard-
ware/software platforms that are used by various
types of networking technologies.
SNMP is applied for collecting data that is used
for management purposes including network delay to-
mography. SNMP (Zhao et al., 2006) periodically
polls statistics such as byte count of each link in an IP
network. In SNMP, the commonly adopted sampling
interval is 5 minutes. The management station cannot
start the management information base (MIB) polling
for hundreds of the router interfaces in a network at
the same time (at the beginning of the 5-minutes sam-
pling intervals). Therefore, the actual polling inter-
val is shifted and could be different than 5 minutes.
This polling discrepancy becomes a source of error in
SNMP measurements.
The traffic flow statistics are measured at each
ingress node via NetFlow (Clemm, 2006), (Systems,
2010). A flow is an unidirectional sequence of pack-
ets between a particular source and destination IP ad-
dress pair. The high cost of deployment limits the
NetFlow capable routers. Also, products from ven-
dors other than Cisco have limited or no support at all
for NetFlow (Clemm, 2006), (Systems, 2010). There-
fore, sampling is a common technique to reduce the
overhead of detailed flow level measurement. The
flow statistics are computed after applying sampling
at both levels; packet level and flow level. Since the
sampling rates are often low, inference from the Net-
Flow data may be noisy.
Both SNMP and NetFlow use the user datagram
protocol (UDP) as the transport protocol. The oper-
ating nature of UDP may add to the error term of the
model due to hardware or software problem resulting
in data loss in transit (Zhao et al., 2006), (Clemm,
2006), (Systems, 2010).
Having different vendors for network components
along with hardware/software platforms that are used
by various types of networking technologies and the
inherited shortcomings of the distributed computing
also introduce errors. The risk of errors increases if
there are more components in a system. The physical
and time separation and consistency is also a problem
and a source of error (Zhao et al., 2006).
The next section describes related work and dis-
tinguishes our contribution from the related work.
3 REVIEW OF RELATED WORK
The authors of (Zhao et al., 2006), on their way to es-
timate traffic matrix with imperfect information, have
mentioned the presence of errors in network measure-
ments. But, they did not present any solution in par-
ticular to the errors in link measurements. Though
they have considered these errors when they have
DCNET 2010 - International Conference on Data Communication Networking
68

compared the traffic matrix with and with out network
measurement errors.
A traffic matrix quantifies aggregate traffic vol-
ume between any origin/destination (OD) pairs in a
network, which is essential for efficient network pro-
visioning and traffic engineering.
They have applied statistical signal processing
techniques to correlate the data obtained from both
(SNMP and NetFLow) measurement infrastructures.
They have determined traffic under the passive to-
mography by considering a bi-model approach for
error modeling. As they have used one model for
the SNMP errors and another model for NetFlow er-
rors. They have also categorized errors in various cat-
egories such as erroneous data and dirty data. We,
on the other hand, have used a single model to repre-
sent noise irrespective of the nature of noise source as
shown in Equation 2. Our model is simpler as it con-
siders all the errors as a single collective parameter,
ε, irrespective of the sources that have caused these
errors. Though we have collected data for our sim-
ulations by active tomography, our method could be
applied to any type of tomographic data.
As described in Section 2, various kinds of
sources introduce errors in the original data and the
use of this data for making further estimation can mul-
tiply the errors. There is need for a techniques that
may denoise this data and SCS is one of such tech-
niques. A brief description of SCS is given in the next
section.
4 SPARSE CODE SHRINKAGE
(SCS)
SCS (Hyvarinen, 1999) exploits the statistical proper-
ties of data to be denoised. To explain the SCS model,
assume that we observe a noisy version
e
X = x+ν of
the data x, where ν is Gaussian White Noise (WGN)
vector. To denoise
e
X,
1. we transform the data to a sparse code,
2. apply ML estimation procedure component-wise,
3. transform back to the original variables.
Following are the steps involved:
1. Using a noise-free training set of x, use a sparse
coding method for determining the orthogonal
matrix W so that the components s
i
in s = Wx
have as sparse distributions as possible. Orig-
inally, SCS uses ICA in (Hyvarinen, 1999) for
the estimation of the sparsifying transformation.
There are various other ways to implement BSS
such as Principal Component Analysis (PCA) and
Singular Value Decomposition (SVD). In this pa-
per, we use Non Negative Matrix Factorization
(NNMF) instead of ICA for this purpose. The
ICA approach may result in negative values in es-
timated matrices whereas all the involved compo-
nents in NNMF are always positive and the same
is true for link delays. NNMF is briefly explained
in the next section.
2. Estimate a density model p
i
(s
i
) for each sparse
component, using the following two models:
• Model 1: the first model is suitable for super-
gaussian densities that are not sparser than the
Laplace distribution, and is given by the family
of densities:
p(s) = Cexp(
−as
2
2
−b|s|) (2)
where a, b > 0 are parameters to be estimated,
and C is an irrelevant scaling constant. A sim-
ple method for estimating a and b was given in
(Hyvarinen, 1999). For this density, the nonlin-
earity g takes the form:
g(u) = 1/(1 + σ
2
a)sign(u)max(0, |u|−σ
2
)
(3)
where σ
2
is the noise variance.
• Model 2: this model describes densities that are
sparser than the Laplace density:
p(s) =
1
2d
(α+ 2)[
α(α+1)
2
]
(
α
2
+1)
[
q
α(α+1)
2
+ |
s
d
|]
α+3
(4)
When α→infinity, the Laplace density is ob-
tained as the limit. A simple consistent method
for estimating the parameters d, α > 0 can be
obtained from the relations d =
√
Es
2
and α =
(2−k+
√
K(K+4))
(2k−1)
. The resulting shrinkage func-
tion can be obtained as below:
U =
1
2
q
(|u|+ ad)
2
−4σ
2
(α+ 3) (5)
g(u) = sign(u)max(0,
|u|−ad
2
+U) (6)
Where a =
q
α(α+1)
2
and g(u) is a set of zeros
in case the square root in the above equation
is imaginary. Compute for each noisy obser-
vation
e
X(t) of X, the corresponding sparse
component. Apply the shrinkage no-linearity
g
i
(.) as defined in the above equations for g(u)
on each component y
i
(t) for every observation
DENOISING NETWORK TOMOGRAPHY ESTIMATIONS
69

index t. Denote the obtained component by
S
i
(t)= g
i
(y
i
(t)).
3. Invert the relationship, s=Wx, to obtain estimates
of the noise free X, given by ex(t)= W
e
X(t).
To estimate the sparsifying transform W, an access to
a noise-free realization of the underlying random vec-
tor is assumed. This assumption is not unrealistic in
many applications: for example, in image denoising
it simply means that we can observe noise free im-
ages that are somewhat similar to the noisy image to
be treated, i.e., they belong to the same environment
or context. In terms of link delays in networking it
means having link delay readings while a system is
operating in normal condition with no abnormalities
to cause errors.
5 NON NEGATIVE MATRIX
FACTORIZATION (NNMF)
Non Negative Matrix Factorization (NNMF) is one
of the implementations of Blind Source Separation
(BSS). If a non negative matrix V is given, then the
NNMF finds non-negative matrix factors W and H
such that (Cichocki et al., 2009):
V ≈WH (7)
To find an approximate factorization, a cost function
is defined that quantifies the quality of the approxima-
tion. Such a cost function can be constructed using
some measure of distance between two non negative
matrices, A and B. One popular cost function is sim-
ply the square of the Euclidean distance between A
and B,
kA−Bk
2
=
∑
(A
ij
−B
ij
)
2
(8)
and another is based on divergence,
D(AkB) =
∑
ij
(A
ij
log
CA
ij
B
ij
−A
ij
+ B
ij
) (9)
For each cost function, there are rules for updating W
and H after selecting initial values of W and H. At
each iteration W and H are multiplied and kV-WH k
2
or D(V k WH) is calculated. The values of W and H
are updated until kV-WH k
2
or D(V k WH) reach a
minimum threshold. At this moment, the values of W
and H represent the final estimate.
5.1 Sparsity with NNMF
A useful property of NNMF is the ability to produce
a sparse representation of data. Such a representation
encodes much of the data using a few active compo-
nents, which makes the encoding easy to interpret.
On theoretical grounds, sparse coding is considered
useful middle ground between completely distributed
representations on one hand and unary representa-
tions on the other (Cichocki et al., 2009). In terms of
network terminology, a highly sparse network means
using a fewer links out of the total number of links
available in a network and low sparse network means
closer to the original topology of a network. As the
feature of sparsity plays a significant role in SCS, so
NNMF has been considered for the estimation of the
sparsifying transformation in the initial step of SCS.
6 SIMULATION RESULTS OF
DENOISING TOMOGRAPHY
DATA THROUGH SCS
For validating SCS as a technique to denoise the er-
roneous link delays, we designed a test bed to collect
real link delays. We introduced WGN into the mea-
sured link delays to create the affect of errors in the
measured link delays. We input this erroneous data
to SCS and denoised this data to get an estimate of
the link delays close to the measured link delays. The
next subsection describes the test bed that was used
for data collection to obtain end to end delays and link
delays for bench marking.
6.1 Description of Networking Test Bed
We set up a test bed in the Advanced Internetworking
Laboratory (AIL) at Dalhousie University that con-
sists of six 38 series Cisco routers, Agilent Router
Tester (N2X), and a Multi Router Traffic Grapher
(MRTG) capable workstation. OSPF routing has been
implemented on routers and N2X.
The test bed is of smaller size and has limited
number of links, because we have to collect the actual
values of the error free link delays for bench marking
the accuracy of estimated link delays. As no related
work is available to bench mark our novel contribu-
tion, the original link delays remains the only choice
for bench marking. In contrast to this test bed, the
practical networks are larger in scale, but scalability
is not an issue as SCS (Hyvarinen, 1999) and NNMF
(Cichocki et al., 2009) both can handle larger sizes of
matrices.
The Echopath option of the Cisco Service Level
Agreement (CSLA) was implemented. All probes
were grouped together. All the probes in the group
start at the same time. The group of probes was re-
DCNET 2010 - International Conference on Data Communication Networking
70

peated 100 times with a time difference of 10 sec be-
tween two consecutive repetitions. The results of 200
runs were averaged. The MRTG enabled workstation
verified the end to end RTT.
Figure 1 shows a test bed with the four probes
(traveling from right to left) and two of the links
(Link1 and Link6) were stressed with an extended
ping of 200 Bytes. The other source of disturbance
was the traffic from the Agilent router tester (N2X).
The condition of the network remains unchanged dur-
ing the CSLA operation.
Figure 1: Testbed Setup with a mixture of extended pings
and N2X traffic.
6.2 Use of Data from Test Bed
The data obtained from the CSLA is in the form of
accumulative hop-wise round trip time, the following
steps are followed to process the data for obtaining
two matrices; a matrix of end to end delays and a ma-
trix of link level delays.
A parsing software, written in java, extracts link
delays and end to end delays in the form of two ma-
trices. From the accumulative round trip time from
source to each hop, hop to hop delays are calculated to
form the delay matrix. From the accumulative round
trip time (from the source to the destination), end to
end delay matrix is determined. This data has been
used as a baseline for judging the accuracy of the
SCS.
The WGN was simulated through a Matlab based
function and measured link delays were converted
into the noisy link delays. This noisy data was used
as an input to SCS. We expected SCS to denoise this
noisy data in such a way that the denoised link delays
are closer to measured link delays.
As part of the SCS, we needed to apply a BSS
technique as a sparse coding method for determining
the orthogonalmatrix W so that the components s
i
in s
= Wx have as sparse distributions as possible. We ap-
plied NNMF for this purpose. The end to end link de-
lays obtained from CSLA were input to NNMF. The
Matlab tool NMFpack (Hoyer, 2004) had been used
for NNMF factorization . The NMFpck Matlab pack-
age implements and tests NNMF with the feature of
sparsity. Various combinations of measured link de-
lays and the routing matrix with various sparsity lev-
els were tried to get s
i
as sparse as possible. These
sparse estimation of s
i
were input to step 2 of the im-
plementation of SCS as described Section 3.
6.3 Comparison of Measured, Errored,
and Denoised Link Delays
The results have been displayed in six diagrams (Fig-
ure 2 to Figure 7). Each diagram representing one
link, from Link1 to Link6. In each diagram, three
types of data lines are shown:
1. the actual measurement of the link delays col-
lected from CSLA is shown as solid lines in
graphs,
2. the link delays after the introduction of the error
are shown as the dotted lines,
3. the denoised link delays after the application of
SCS are shown as dashed lines.
The vertical axis represents the link delays and hori-
zontal axis is the number of samples at various times.
It is clear from these six graphs that the denoised
link delays are very close to the actual link delays.
The errored link delays were input to SCS and the es-
timated (denoised) values of link delays are close to
the measured values. This shows that the SCS has
successfully denoised the noisy link delay data and
the denoised data is in the proximity of benchmarks.
Figure 2: Comparison of measured, errored, and denoised
link delays on Link1.
7 CONCLUSIONS
High quality traffic measurements are a key to suc-
cessful network management. Direct observation of
the desired statistics in a network is not possible with-
out the special cooperation of the internal network
resources. Network tomography facilitates indirect
estimation of the desired network parameters. Vari-
ous sources introduce errors in the estimated parame-
DENOISING NETWORK TOMOGRAPHY ESTIMATIONS
71
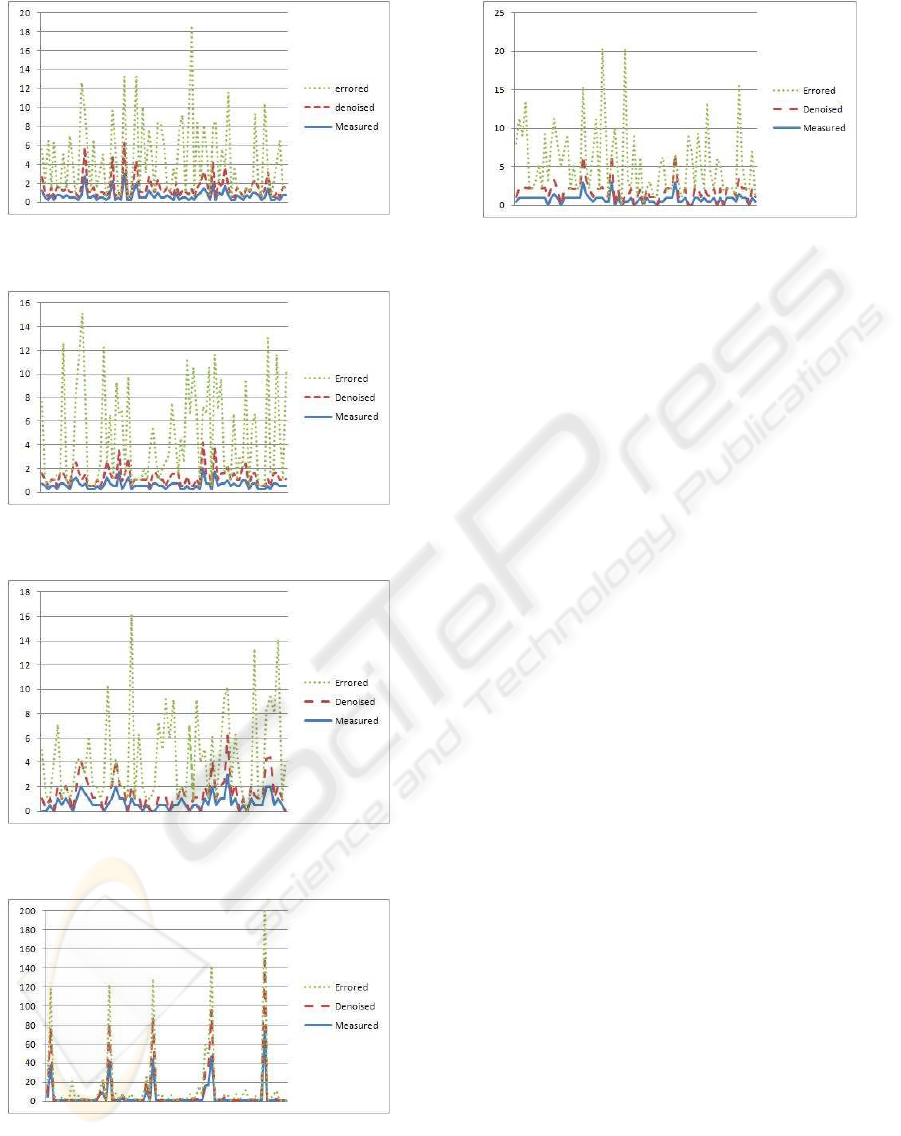
Figure 3: Comparison of measured, errored, and denoised
link delays on Link2.
Figure 4: Comparison of measured, errored, and denoised
link delays on Link3.
Figure 5: Comparison of measured, errored, and denoised
link delays on Link4.
Figure 6: Comparison of measured, errored, and denoised
link delays on Link5.
ters and reduce the effectiveness of the estimated pa-
rameters. We applied the technique of sparse shrink-
age coding (SCS) to denoise the network tomography
Figure 7: Comparison of measured, errored, and denoised
link delays on Link6.
model with errors. To fit well to our research objec-
tives, we modified SCS by replacing ICA with NNMF
to get all the positive values in the estimated link de-
lay matrices. The results obtained from the laboratory
test bed based simulations proved that SCS success-
fully denoised the link delays. The comparison of de-
noised link delays with the error free benchmark data
showed them very close to each other.
REFERENCES
Castro, R., Coates, M., Liang, G., Nowak, R., and Yu, B.
(2004). Network tomography: Recent developments.
In Statistical Science. Volume 9, 499–517.
Cichocki, A., Zdunek, R., Phan, A. H., , and ichi Amari,
S. (2009). Nonnegative Matrix and Tensor Factor-
izations: Applications to Exploratory Multi-way Data
Analysis and Blind Source Separation. Wiley.
Clemm, A. (2006). Network management fundamentals,
ACM SIGMETRICS Performance Evaluation Review.
Cisco Press.
Coates, M. and Nowak, R. (2001). Network tomography for
internal delay estimation. In 2001 IEEE International
Conference on Acoustics, Speech, and Signal Process-
ing, Proceedings (ICASSP’01). IEEE.
Hoyer, P. (2004). Non-negative matrix factorization with
sparseness constraints. In The Journal of Machine
Learning Research. MIT Press Cambridge, MA, USA,
Volume 5.
Hyvarinen, A. (1999). Sparse code shrinkage: Denoising of
nongaussian data by maximum likelihood estimation.
In Neural Computation. Volume 11, 1739–1768, MIT
Press.
Systems, C. (2010). NetFlow Services Solutions Guide.
available at www.cisco.com.
Vardi, Y. (1996). Network tomography: Estimating source-
destination traffic intensities from link data. In Jour-
nal of the American Statistical Association. Volume
91, 365–377.
Zhao, Q., Ge, Z., Wang, J., and Xu, J. (2006). Robust
traffic matrix estimation with imperfect information:
Making use of multiple data sources. In ACM SIG-
METRICS Performance Evaluation Review. Volume
34, 144.
DCNET 2010 - International Conference on Data Communication Networking
72
