
A HIERARCHICAL HANDWRITTEN OFFLINE SIGNATURE
RECOGNITION SYSTEM
Ioana Bărbănţan, Camelia Lemnaru and Rodica Potolea
Department of Computer Science, Technical University of Cluj-Napoca, Cluj-Napoca, Romania
Keywords: Signature Recognition, Hierarchical Classifier, Classification, Clustering, Naïve Bayes, Feature Selection,
Learning Curve.
Abstract: This paper presents an original approach for solving the problem of offline handwritten signature
recognition, and a new hierarchical, data-partitioning based solution for the recognition module. Our
approach tackles the problem we encountered with an earlier version of our system when we attempted to
increase the number of classes in the dataset: as the complexity of the dataset increased, the recognition rate
dropped unacceptably for the problem considered. The new approach employs a data partitioning strategy to
generate smaller sub-problems, for which the induced classification model should attain better performance.
Each sub-problem is then submitted to a learning method, to induce a classification model in a similar
fashion with our initial approach. We have performed several experiments and analyzed the behavior of the
system by increasing the number of instances, classes and data partitions. We continued using the Naïve
Bayes classifier for generating the classification models for each data partition. Overall, the classifier
performs in a hierarchical way: a top level for data partitioning via clustering and a bottom level for
classification sub-model induction, via the Naïve Bayes classifier. Preliminary results indicate that this is a
viable strategy for dealing with signature recognition problems having a large number of persons.
1 INTRODUCTION
The verification and recognition of signatures in an
offline signature recognition system is performed on
data extracted from signatures. The signatures are
written on paper. After gathering the signatures,
several pre-processing techniques are required. The
individual signatures are normalized to fit a standard
format. Because the data acquired is usually noisy
(either due to the scanning process or because of the
pens used in writing) a filter may be applied. Then, a
number of static features are extracted from the
images and the signature dataset is created. An
instance in the dataset consists of an individual
signature; the attributes of an instance are the
features extracted from the signature, while the class
is the owner of the signature. This dataset is used to
train a classifier such as to obtain a classification
model, which is able to determine the owner of a
new signature fed to the system.
Several different learning approaches have been
investigated by the scientific community for
signature recognition and verification systems. In
(Prasad and Amaresh, 2003) the Euclidean distance
in the feature space is employed in conjunction with
an Artificial Neural Networks classifier to obtain a
false acceptance rate of 13.33% on forged
signatures. The Hidden Markov Model has been
implemented by (Ozgunduz, 2005), obtaining a 75%
score on Type I error. In (Justino, 2000), the Support
Vector Machines yields a classification ratio of 95%
and the Artificial Neural Networks obtains an
accuracy of 75%. Another system based on the
Hidden Markov Model may be found in
Justino &
Yacoubi, 2000
.
Perhaps one of the most widely employed
classification methods in signature verification and
recognition systems is the Artificial Neural
Networks (ANN) learner. This is why, in our
approach, we have also focused on this method for
the classification module. Also, initial performance
evaluations on several learners have indicated that
the Naïve Bayes (NB) classifier yields the most
promising results, therefore, it has been chosen as
the most appropriate learner in our approach.
The rest of paper is organized as follows. In
section 2 we introduce some theoretical employed
by our proposed system. Section 3 presents a
139
B
ˇ
arb
ˇ
an¸tan I., Lemnaru C. and Potolea R. (2010).
A HIERARCHICAL HANDWRITTEN OFFLINE SIGNATURE RECOGNITION SYSTEM.
In Proceedings of the 12th International Conference on Enterprise Information Systems - Artificial Intelligence and Decision Support Systems, pages
139-147
DOI: 10.5220/0002974001390147
Copyright
c
SciTePress

theoretical aspects related to techniques and
algorithms model for offline signature recognition.
The first part of section 4 reviews the main
implementation aspects and previous evaluation
results obtained by the offline signature recognition
system we have proposed in (Bărbănţan et al., 2009).
In the second part of section 4 we propose a new
approach for the classification module of the
recognition system and discuss the results of an
initial experimental analysis on this novel
methodology. We conclude the paper with a series
of remarks and proposals for future development.
2 THEORETICAL
BACKGROUND
This section presents the theoretical aspects of the
methods employed in the system. Details about how
the methods are implemented and their usage are
presented throughout the paper.
2.1 Feature Selection
Feature selection is one of the most important pre-
processing steps in pattern recognition and data
mining. It is an effective dimensionality reduction
technique and an essential pre-processing method
for removing irrelevant and/or redundant features,
which are known to have a negative influence on the
classification accuracy of most classifiers.
Some of the widely used techniques in feature
selection are: the wrapper method (Kohavi and John,
1994), the Correlation-based Feature Selection (Hall,
2000) and Ranker (Witten and Frank, 2005) filters.
Correlation based Feature Selection
This filter evaluates the worth of a subset of
features by considering the individual predictive
ability of each feature along with the degree of
redundancy between them; subsets of features that
are highly correlated with the class while having low
inter-correlation are preferred. They are independent
of any classifier. Moreover, the comparative
evaluations performed in (Hall, 2000) have shown
that it achieves a comparable performance to the
wrapper approach in terms of classification
accuracy, while requiring a smaller amount of time
to generate the attribute subset.
The Ranker Filter. The Ranker filter orders
individual attributes according to an individual
score, such as the information gain. Ranker not only
ranks attributes but can also perform attribute
selection by removing the lower-ranking ones.
Wrapper Methods. Wrapper methods employ
performance evaluations on a learning algorithm in
order to estimate the worth of a given attribute
subset. Although much slower than filters wrappers
have been shown to achieve significant performance
improvements in classification (Kohavi and John,
1994).
2.2 Learning Curve
The learning curve is often used as a method
assessing for the variation of the classifier
performance with respect to the variation of the
training set size. The basic technique starts from a
small size training set and progressively increases
the number of instances until the entire available
training set is considered. The convergence criterion
is obtaining a stable, smooth curve, with constant
accuracy.
2.3 Clustering
Unlike classification, clustering does not attempt to
assign a concept label to an instance, but it partitions
the given dataset into clusters containing very
similar instances inside the same cluster, while
dissimilar individuals are spread among clusters.
The goal is to maximize intra-cluster similarity
while minimizing inter-cluster similarity.
The similarity between objects when forming
clusters is determined by using a distance measure.
Among the best known are the Euclidean,
Manhattan and the Minkowski distances (Han and
Kamber, 2006) for numeric attributes, and the
overlap metric for nominal (and binary) attributes.
The clustering techniques are traditionally
grouped into four categories (Halkidi and Batistakis,
2001): partitional clustering, hierarchical clustering,
density-based clustering and grid-based clustering.
Perhaps the best known clustering technique is k-
Means – a partitional approach. It is an iterative
technique which performs several steps to reach the
final clusters. The algorithm takes as input k, the
number of clusters to be created. Initially, the k
cluster centres (centroids) are selected at random
from the dataset. In each step, the instances are
distributed into the appropriate clusters, by
computing the distance between the instance and
each cluster centroid. The instance is then assigned
to the closest cluster. After all instances have been
distributed into the current clusters, the cluster
centroids are recomputed and a new iteration begins.
The algorithm terminates when no more re-
assignments occur. The advantages of this method
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
140

include computational efficiency, fast
implementation, while the disadvantages refer to the
random initialization of the k cluster centers
(centroids) and the requirement of specifying k (i.e.,
k is not a result of data-specific properties) (Saitta et.
al., 2007).
3 A MODEL FOR OFFLINE
SIGNATURE RECOGNITION
This section presents a theoretical model for our
offline signature recognition. The model contains the
flow of the data acquisition process and a model for
tuning the classification module.
3.1 Data Acquisition Process
The flow of the data collection process follows the
diagram in Figure 1.
Figure 1: Data collection flow diagram.
Collection of Data. The signatures are initially laid
down on white sheets of paper. Following a
scanning and cropping stage, the standard format
images of the signatures are obtained.
Pre-processing. To remove the noise which may be
introduced during the scanning process, a filter is
employed. The images are then binarized, as the
interest is in the distribution of the pixels and not
their colour intensity.
Because of the different pens used in writing and
because of the scanning process, the signatures do
not have the same widths, so normalization step is
required (Azar, 1997).
Feature Extraction. A number of static features are
extracted from the one-pixel width signature image,
to create a signature instance. Each signature
instance is stored in the signature database to create
the signature dataset.
3.2 Classification and Recognition
Module
The classification and recognition module performs
the actual recognition task. Several steps have to be
considered in order to reach a robust working
system. These steps are presented in Figure 2.
Figure 2: Classification and recognition diagram.
Performance. The main factor in establishing the
performance of the system is the classification
accuracy. Since the recognition problem has a
uniform cost (i.e. we are equally interested in
identifying all signatures correctly), an error-based
metric such as the accuracy is appropriate.
Tuning
Several tuning steps have to be considered, the
most important being dataset tuning and algorithm
tuning. Dataset tuning refers to finding the optimal
number of training instances per class, such that the
accuracy of the induced classification model remains
at a high level as the diversity of the data (i.e. the
number of classes) increases. This is achieved by
analyzing the learning curve built on the available
data.
Algorithm tuning establishes which learning
method is more appropriate and which are the best
parameter settings for it. Of course this step must
take advantage of previous work performed in the
field.
A HIERARCHICAL HANDWRITTEN OFFLINE SIGNATURE RECOGNITION SYSTEM
141

The Classification Model. The working
classification model is induced from the tuned
dataset, using the learning algorithm and the
appropriate parameters determined in the algorithm
tuning phase. When a new signature instance arrives
in the system, it is assigned a label (a person name)
by the classification model.
4 A PROPOSED SYSTEM FOR
OFFLINE SIGNATURE
RECOGNITION
In this section we review the main implementation
aspects and previous evaluation results obtained by
the offline signature recognition system we have
previously proposed in (Bărbănţan et al., 2009). In
the second part of this section we propose a new
approach for the classification module of the
recognition system and discuss the results of an
initial experimental analysis on this novel
methodology.
4.1 Data Collection
The data has been collected from 84 individuals
belonging to different age groups. Each individual
has provided approximately 20 signatures. The
signatures are initially collected on a white A4 sheet
of paper, using either pens or pencils. Each sheet of
paper contains 10-20 signatures. The scanning
process is performed at a resolution of 150 dpi. Each
signature is cropped into a 400x400 pixel frame.
Signatures that do not fit this format are discarded.
The individual signatures are then saved as 256
color bitmaps.
The first pre-processing step performed, as the
diagram in Figure 1 shows, is image enhancement:
the noise introduced by scanning is removed using a
median filter. Then, the image is binarized and
skeletonization method is applied, using Hilditch’s
algorithm (Azar, 1997).
Extracted Features. We have employed a set of
global static features extracted from the signature
image, all having numerical values. Some of the
employed features can be found in similar systems,
(Justino, 2000), (McCabe, 2008), (Amaresh and
Prasad), and we also proposed two new features.
The 25 features considered in our system, have been
grouped into 5 categories, as shown in Table 1. The
first category of features contains the two new
introduced features which are distance based: Top-
bottom Euclidean distance and Left-right Euclidean
distance. They measure the Euclidean distance from
the leftmost and rightmost pixel and from the top to
the bottom pixel. By using feature selection method,
these attributes are selected as being relevant.
Table 1: The extracted features grouped into categories.
* represents the original features proposed.
Attribute
categories
N
umber
of
attributes
Category
name
1. Features obtained
from the extreme
p
oints
6+2* Border
features
2. Features extracted
from the histo
g
ra
m
6 Concentratio
n features
3. Features related to
the number of pixels
4
N
umber
features
4. Features obtained
with respect to the
p
ixel position
4 Position
features
5. Features having as
result an angular
value
3 Angle
features
The content of the categories is the following:
• Border Features = {Width, Height, Left-right,
Top-bottom, Area, Aspect ratio, Signature area,
Width/Area}
• Concentration Features = {Maximum value of
horizontal and vertical histogram, Number of
local maximum of horizontal and vertical
histogram, Top heaviness, Horizontal
dispersion}
• Number Features = {Number, Edge points, Cross
points, Mask feature}
• Position Features = {Sum of X and Y positions,
Horizontal and vertical centre of the signature}
• Angle Features = {Inclination, Baseline slant
angle, Curvature}
Dataset Structure. Following a cleaning stage, in
which we removed the signature images which were
too noisy, we have ended up with a dataset
containing 1548 instances, labelled into 84 classes.
For the tuning and evaluation activities we have
employed several strategies: either repeated 80-20
percentage splits, or 10-fold cross validation.
4.2 Classification
For the classification module we have considered
two Bayesian classifiers and the Multilayer
Perceptron (MLP). The two Bayesian classifiers
used are the Naïve Bayes and the BayesNet.
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
142

4.2.1 Feature Selection
Since we have employed a large set of features
coming from different sources, and also added two
new features, we have performed feature selection to
find the optimal subset of features, by eliminating
the irrelevant and redundant features. We have
applied the following strategy: the attributes are first
ordered by their importance with respect to the class
by using the Ranker filter. Then two other methods
were used: the CFS filter and the wrapper method,
whose results are combined such that the most
promising subset is obtained. We employed the
implementations found in Weka (Witen and Frank,
2005) for the three methods, with their default
parameters.
Ranker Filter. We have employed the information
gain evaluator to measure the importance of each
attribute for the class. The ranking of the attributes
was used when combining the results of the other
two methods.
CFS Filter. The CFS filter removes the attributes
which are weakly correlated with the class and/or
strongly correlated with other attributes. With the
CFS filter 15 attributes are selected as being
relevant, from the
total set of 25 attributes.
Wrapper Method. For the wrapper approach we have
employed a specialization of the 3-tuple wrapper:
<generation, evaluation, validation>, using the
Naïve Bayes (NB) classifier in the evaluation
function. MLP has not been considered because its
performance on preliminary evaluations was 5%
below that of NB, and previous work (Vidrighin et
al., 2008) suggests that feature selection does not
affect the initial ranking of classifiers, meaning that
the best classifier on the initial set of features yields
the highest performance on the reduced set as well.
The wrapper method selected a subset of 18
attributes as best describing the instances.
The subset of attributes selected by the CFS filter
and the one generated by the Wrapper method has a
number of 12 common attributes. One of the two
features introduced by us was selected as being
relevant by both of the methods.
After selecting the common attributes, some of the
remaining attributes were added to the subset in the
order generated by ranker. In the end a subset of 23
attributes was obtained as being the most
representative.
4.2.2 Learning Curve Analysis
Having generated the dataset, we wanted to evaluate
the way the number of instances influences the
classification accuracy of our system. That is why
we performed several learning curve experiments.
We started with a maximum of 20 instances/class
and observed that the learning curve had still an
ascending aspect. Therefore, we decided to collect
more instances from each class. We estimated that
25 instances per class were needed. When evaluating
the performance in the new context, we noticed the
classification accuracy decreased while increasing
the number of classes. Besides the lower accuracy,
another problem is that, in a real application, it is
unfeasible to collect such a large number of sample
signatures from a person for authentication. These
drawbacks indicate that a different approach should
be considered.
4.3 A New Approach for the
Classification Module
Our previous work reported a stable learning curve,
for the accuracy value as a function of number of
instances/class. However, stability is obtained for a
lower accuracy value which suggests the need of a
different approach.
4.3.1 Preliminary Investigations
Figure 3: Learning curve with increasing number of
classes and 20 instances/class.
We have restarted the experiments with 84 classes,
20 instances per class. The approach this time was to
identify the optimal pair <number of instances per
class, number of classes per dataset> in terms of
accuracy. From the analysis of the learning curve it
resulted that between 50 and 55 classes the curve is
stable and the accuracy is acceptable, while after 55
A HIERARCHICAL HANDWRITTEN OFFLINE SIGNATURE RECOGNITION SYSTEM
143

classes the performance degradation becomes
unacceptable.
In the attempt to evaluate the minimum optimal
number of instances/class, we run an experiment on
a 55 class dataset. The learning curve obtained is
presented in Figure 4. It emphasizes a minimum
number of 11 instances/class for an acceptable
accuracy. Moreover, the curve becomes stable (with
a less steep slope), that is why our expectations are
that the optimum number of instances per class to be
found in the interval [11,20].
Figure 4: Learning curve with increasing number of
instances/class and 55 classes.
This suggests that we should find a technique which
has to consider fewer classes in training a
classification model.
Because speed is also an issue in signature
recognition systems and because we cannot collect a
large number of reference signatures from the same
person, we have performed a series of experiments
with 11 up to 16 instances per class, to determine the
best number of training instances/class. We have
varied the number of classes between 5 and 84,
using a 5 class increment.
As shown in Figure 5, the performance of the NB
classifier degrades as the number of classes
increases, just like in the case of the 20
instances/class learning curve in Figure 3. This
suggests that we need to employ a data partitioning
criterion in the training phase, and build
classification sub-models on smaller datasets (with
fewer classes). Also, a number of 11 or 14 instances
per class seem to yield high accuracies.
Figure 5: Clustering using different number of
instances/class and 84 classes.
4.3.2 A Hierarchical, Data-partitioning
based Approach
The new approach we propose employs a
hierarchical strategy: first split the initial dataset in
several subsets via a clustering method, and
subsequently supply each subset to the NB classifier,
for building classification sub-models (Figure 6).
Figure 6: Generic training process of the hierarchical
classifier.
When a new instance arrives and needs to be
classified, the hierarchical classifier first clusters the
instance to find the best classification sub-model for
it. It then feeds the instance to that classification
sub-model, which assigns the class label to the
instance (Figure 7).
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
144
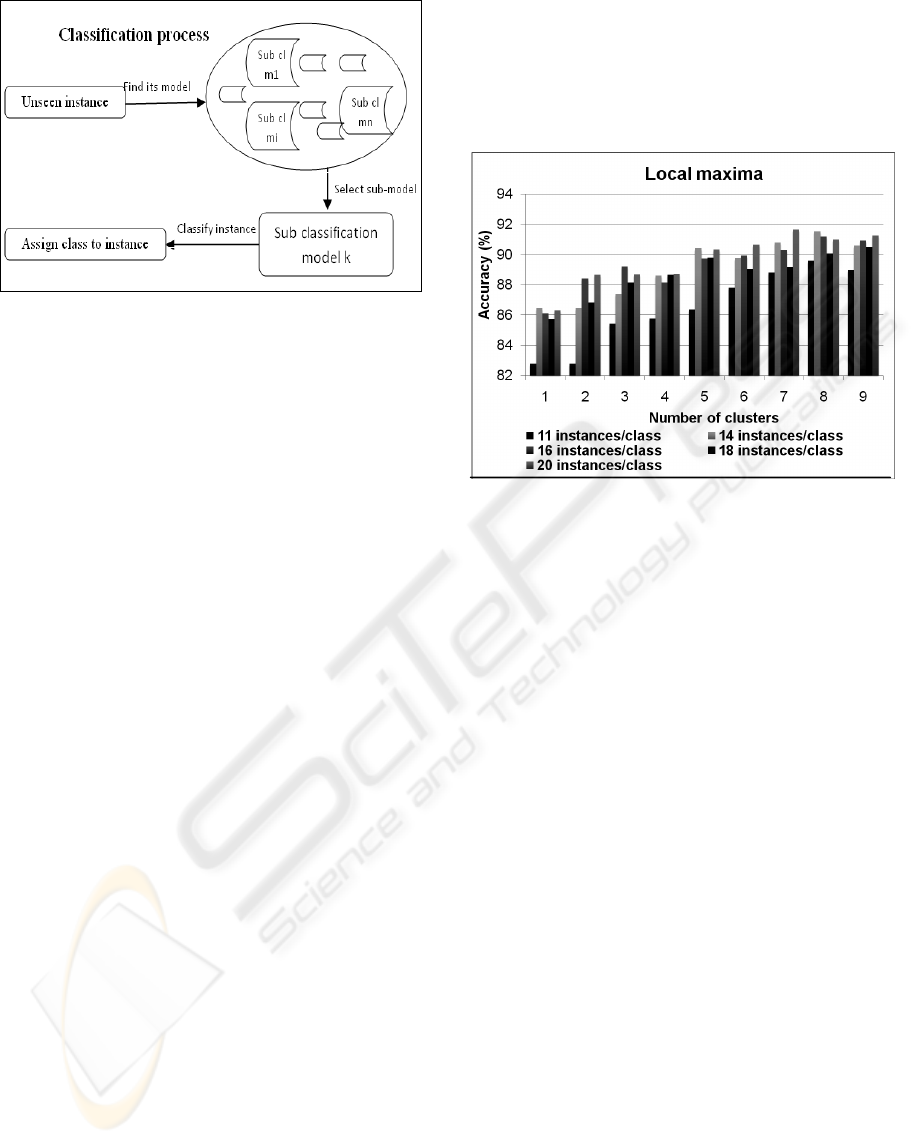
Figure 7: Generic classification process for the
hierarchical classifier.
Clustering is a technique that groups similar
instances together. For the purpose of our
recognition system, we are interested that the
instances from a single class are gathered (as much
as possible) by the same cluster. Since the
approximate number of clusters can be estimated
apriori from the total number of classes and the
approximate number of classes we want in each
classification sub-model (which follows from careful
analysis of the diagram in Figure 5), we have
decided to employ k-Means as clustering method.
In the attempt to develop a working functional
classification module, we have performed a series of
evaluations meant to help establish optimal settings
for a number of parameters in our new system, the
most important being the optimal number of clusters
(i.e. classification sub-models) and the optimal
number of instances per class.
For these investigations we have employed the
SimpleKMeans implementation from the Weka
framework of the k-Means clusterer.
Because the available data contains classes
which do not have exactly 20 instances (due to the
initial data cleaning), we have removed these classes
to obtain a dataset with a uniform distribution.
Therefore, the next experiments were conducted on
a dataset having 76 classes, each with exactly 20
instances.
The purpose of our next experiments is to
determine the optimal number of clusters to use,
such as to obtain acceptable sizes for the training
subsets, while preserving a good cluster purity.
Therefore, we performed clustering experiments
with versions of the training set containing 11, 14,
16, 18 and 20 instances per class. For each
experiment, we have varied the number of clusters
between 1 (no clustering at all) and 9.
A first observation can be made on the speed of the
clustering process: as we increased the number of
clusters, the speed was dramatically reduced. While
for k=2 the results were almost instantaneous on all
datasets considered, it took the algorithm 2 days to
complete the clustering process for k=9.
Figure 8: Performance analysis of the sub-models induced
from clustering with 1-9 clusters, on the datasets having
11, 14, 16, 18 and 20 instances per class.
The next step in training the hybrid classifier is to
form the classification sub-problems – generate the
reduced training sets for each cluster – and feed
them to the NB classifier. Although this step is not
yet connected with the clustering step, we have
performed initial evaluations to assess the
performance of the NB classifier on these reduced
training sets (containing fewer, but very similar
classes). When performing clustering, for some
classes not all the instances fall in the same cluster,
so the clusters are not pure. To solve this issue,
when forming the training subsets, we have placed
all the instances in one class inside the subset
corresponding to the cluster with the largest number
of instances from that class.
These subsets were then fed to NB classifiers and we
evaluated the classification accuracy of the sub-
models induced, using a 10-fold cross-validation
loop. The results are presented in Figure 8.
The results indicate that none of the evaluated
dataset settings (i.e. number of instances per class)
outperforms all the others for all types of
partitioning (i.e. number of clusters evaluated).
However, most of them seem to have several local
maxima. Figure 9 clearly shows the existence of
partitioning intervals in which different pairs of
settings perform the best.
A HIERARCHICAL HANDWRITTEN OFFLINE SIGNATURE RECOGNITION SYSTEM
145
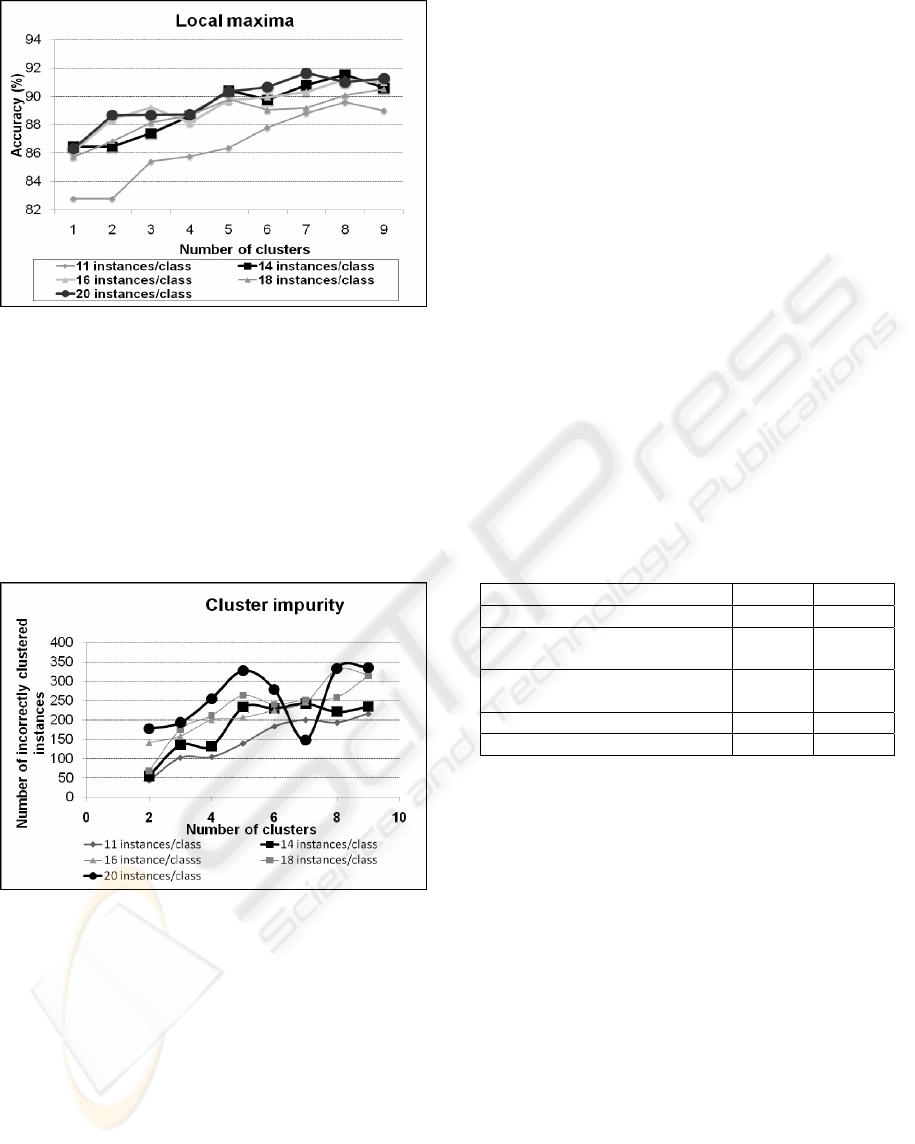
Figure 9: Curves representing the local maxima when
partitioning into clusters.
Therefore, a maximum can be selected. In doing so
we must also consider the cluster purity – to be
discussed shortly. The performance slopes in Figure
9 indicate that either 14 or 20 instances/class should
be considered, for a 6-9 cluster partitioning.
However, the number of clusters should be adjusted
for each dataset, current evaluations indicating a
1/10 ratio on the number of clusters/classes.
Figure 10: Curves representing the impurity of clusters for
different number of instances/class and 76 classes.
We expect that the way the instances are grouped
into clusters affects the performance of the entire
system. We define impurity as the number of
instances that do not belong to the cluster containing
the largest number of instances from the given class.
We have performed an analysis of the impurity of
the clusters. The results are presented in Figure 10.
Generally, as we increase the number of instances
per class the impurity of the clusters increases also.
The cluster impurity affects the second step in the
training process, i.e. inducing the sub-models for
classification. A small cluster impurity is thus
preferable.
As a consequence, when tuning the number of
instances per class to use for training and the number
of clusters in which the classes should be split into, a
trade-off between the accuracy and the impurity has
to be made. The analyses of the results indicate as
optimal the values in Table 2. These values are
particular for this dataset. However, they indicate
that we can achieve the same performance if we
decrease the size of the classification sub-problems
when the number of available instances per class is
relatively small (we achieved the same performance
with 14 instances per class and 8 clusters as with 20
instances per class and 7 clusters). This suggests
that, as the number of classes increases, we might
have to consider a 2-stage clustering process, such as
to obtain relatively small sub-classification
problems. Also, we need to consider the time aspect.
The speed of building the models for 7 and 8
clusters is significantly better than the speed of
building a 9-cluster model.
Table 2: Optimal number of instances per class and the
corresponding number of clusters.
Number of instances/class 14 20
Optimal number of clusters 8 7
Minimum number of
classes/cluster
4 4
Maximum number of
classes/cluster
17 20
Mean number of classes/cluster 9.5 10.85
Accuracy ~91% ~91%
5 CONCLUSIONS AND FUTURE
WORK
This paper presents a new method for classifying
handwritten signatures using a hierarchical data-
partitioning based approach. The new method
tackles the problem we encountered with an earlier
version of our system when we attempted to increase
the number of classes in the dataset: as the
complexity of the dataset increased, the recognition
rate dropped unacceptably for the problem
considered – from 98.53 on a 5-class problem to
84.37 on an 84-class problem. The new method
combines a clustering mechanism and a Bayesian
classifier. Various experiments were performed in
order to determine the optimal number of clusters to
divide a given dataset and the number of instances to
use from each class.
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
146

Preliminary results yield an accuracy of more than
91%, with the entire set of attributes, without using
feature selection. We consider that feature selection
will further boost the classification accuracy. We
also managed to improve the classification time by
using a smaller number of instances per class (14).
The results have also shown that peak
performances are obtained on a 14 instances/class
dataset using 8 clusters and a 20 instances/class
dataset using 7 clusters.
Our current work focuses on connecting the two
steps of the training process, and addressing the
classification stage. Also, for generalizing the scope
of the system, during the training process several
issues need to be considered.
The first is that the classes are not split uniformly
into clusters (instances from the same class are
distributed among at most 4 clusters). At present, we
solve this issue by adding all the instances to the
cluster having the maximum number of instances
from that particular class. However, on a global
model, such situations should have a specific
approach. A possible solution is to distribute all the
instances of a class to all clusters which contain a
number of instances above a threshold from that
class. We need to investigate how this approach
influences the complexity, the performance and the
time of the induced sub-models, as it may produce
the necessity of an additional clustering step.
A second issue which needs addressing is the
time required for the SimpleKMeans method to split
the dataset into clusters. We experimentally
observed that the clustering time increases with the
number of clusters. As for 2-5 clusters it takes
several minutes to build the clusters, for values like
8 or 9 clusters, the time required is of up to 2-3 days.
Moreover, as the number of classes increases, we
might need to introduce additional clustering steps.
We are currently evaluating a methodology for
automatically establishing the parameters of the
hierarchical structure: number of clustering levels,
number of clusters per level, optimal size (in terms
of number of classes) of the training subset
submitted to the Naïve Bayes classifiers.
ACKNOWLEDGEMENTS
Research described in this paper was supported by
the IBM Faculty Award received in 2009 by Rodica
Potolea from the Computer Science Department at
the Technical University of Cluj-Napoca, Romania.
REFERENCES
Azar, D., 1997.“Hilditch's Algorithm for Skeletonization”,
Pattern Recognition course, Montreal.
Bărbănţan, I., Vidrighin, C., Borca, R., 2009. “An Offline
System for Handwritten Signature Recognition”,
Proceedings of IEEE ICCP, pp. 3-10.
Halkidi, M., Batistakis, Y., Vazirgiannis, M., 2001. “On
Custering Validation Techniques”, Journal of
Intelligent Information Systems, 107–145.
Hall, M.A., 2000. “Correlation based Feature Selection for
Machine Learning.” Doctoral dissertation,
Department of Computer Science, The University of
Waikato, Hamilton, New Zealand.
Han, J., Kamber, M., 2006. “Data Mining – Concepts and
Techniques”, Morgan Kaufmann, 2
nd
edition.
Justino, J., R., Yacoubi, A., 2000. “An Off-Line Signature
Verification System Using Hidden Markov Model and
Cross-Validation”, Proceedings of the 13th Brazilian
Symposium on Computer Graphics and Image
Processing.
Kohavi, H., John, R., Pfleger, G., 1994. “Irrelevant
Features and the Subset Selection Problem”, Machine
Learning: Proceedings of the Eleventh International
Conference, 121-129, Morgan Kaufman Publishers,
San Francisco.
McCabe, A., Trevathan, J., Read, W., 2008. “Neural
Network-based Handwritten Signature Verification”,
Journal of Computers, Vol 3, No.8.
Ozgunduz, E., Senturk, T., 2005. “Off-line Signature
Verification and Recognition by Support Vector
Machines”, 13
th
European Signal Processing
Conferenece, Antalya.
Prasad, A., G., Amaresh, V., M. An Offline Signature
Verification System.
Saitta, S., Raphael, B. and Smith, F.C.I., 2007. “A
Bounded Index for Cluster Validity”, Proceedings of
the 5th international conference on Machine Learning
and Data Mining in Pattern Recognition - Lecture
Notes In Artificial Intelligence; Vol. 4571, Springer-
Verlag, pp. 174-187.
Vidrighin, Bratu, C., Muresan, T., Potolea, R., 2008.
“Improving Classification Accuracy through
Feature Selection”, Proceedings of IEEE ICCP, pp.
25-32.
Witten, I., R., Frank, E., 2005. Data Mining,”Practical
Machine Learning Tools and Techniques”, Morgan
Kaufmann Publishers, Elsevier Inc.
A HIERARCHICAL HANDWRITTEN OFFLINE SIGNATURE RECOGNITION SYSTEM
147
