
A DISTRIBUTED ALGORITHM FOR FORMAL CONCEPTS
PROCESSING BASED ON SEARCH SUBSPACES
Nilander R. M. de Moraes, Luis E. Z
´
arate and Henrique C. Freitas
Informatics Institute, Pontifical Catholic University of Minas Gerais, Dom Jos
´
e Gaspar av., Belo Horizonte, Brazil
Keywords:
Formal concept analysis, FCA, Information retrieval.
Abstract:
The processing of dense contexts is a common problem in Formal Concept Analysis. From input contexts,
all possible combinations must be evaluated in order to obtain all correlations between objects and attributes.
The state-of-the-art shows that this problem can be solved through distributed processing. Partial concepts
would be obtained from a distributed environment composed of machine clusters in order to achieve the final
set of concepts. Therefore, the goal of this paper is to propose, develop, and evaluate a distributed algorithm
with high performance to solve the problem of dense contexts. The speedup achieved through the distributed
algorithm shows an improvement of performance, but mainly, a high-balance workload which reduces the
processing time considerably. For this reason, the main contribution of this paper is the distributed algorithm,
capable of accelerating the processing for dense formal contexts.
1 INTRODUCTION
Formal Concept Analysis (FCA) is a field of math-
ematics presented in the 1980’s (Ganter, 2002; Gan-
ter and Wille, 1997). The main goal of FCA is in
the knowledge representation based on specific di-
agrams named Hasse Diagrams (Carpineto and Ro-
mano, 2004). In the 2006 edition of the International
Conference on Formal Concept Analysis (ICFCA),
in Desdren, the challenge to process high-dimension
contexts was presented and, as an example, a context
of order 120,000 objects and 70,000 attributes were
mentioned. For this reason, traditional and sequencial
algorithms have high computational cost, and conse-
quently, a high execution time. This characteristic
shows that the extraction of all formal concepts based
on a high dimension context is not feasible.
So a possible solution to process high-dimension
formal contexts is through a distributed algorithm.
Partial formal concepts would be processed in several
nodes in order to achieve a distributed and parallel be-
havior capable of reducing the execution time.
Mathematics formalism was proposed by several
researchers to explore distributed systems focused on
Formal Concept Analysis (Qi et al., 2004; Hu et al.,
2007; Fu and Nguifo, 2003). However, related work
does not present the impact evaluation of context den-
sity in the final performance. Moreover, the related re-
sults have a lack of information about used resources,
such as environment configuration, number of com-
puters, and more details from the cluster.
According to this problem, this paper presents a
strategy to process dense contexts. Therefore, the
main goal of this paper is to present a distributed al-
gorithm focusing on development methodology and
performance evaluation. The distributed algorithm
achieves a speedup up to 139 relative to a sequential
algorithm to solve the same workloads. For this rea-
son, in accordance with the problem statement and
lack of information from related work, the main con-
tribution of this paper is the distributed algorithm. It
is necessary to highligh that Formal Concept Analysis
is very important for fields such as data mining, social
networks and knowledge search, and a distributed al-
gorithm can represent an alternative approach for fea-
sible processing of high dimension contexts.
This article is divided into 6 sections. The fol-
lowing section presents the theoretical foundations of
Formal Concept Analysis. In the third section are pre-
sented the related work. The fourth section presents
the proposed algorithm. Section 5 presents an exper-
imental analysis of the distributed algorithm. Finally,
section 6 presents a brief conclusion and points out
future works.
105
R. M. de Moraes N., E. Zárate L. and C. Freitas H. (2010).
A DISTRIBUTED ALGORITHM FOR FORMAL CONCEPTS PROCESSING BASED ON SEARCH SUBSPACES.
In Proceedings of the 12th International Conference on Enter prise Information Systems - Databases and Information Systems Integration, pages
105-111
DOI: 10.5220/0002976801050111
Copyright
c
SciTePress

2 FORMAL CONCEPT ANALYSIS
In this section the theoretical fundaments of the For-
mal Concept Analysis will be presented. A more care-
ful review about this subject can be found in (Ganter
and Wille, 1997).
2.1 FCA Overview
In the Formal Concept analysis (FCA) a Formal Con-
text is a basic structure used to represent a given data
base through a cross table (formal context). In the Ta-
ble 1 an example of Formal Context for a hipothetical
domain is presented. Such Table represents a struc-
ture that defines objects (lines), attributes (rows), and
their respective incidence relations.
Table 1: Example of a formal context.
a b c d e f g h
1 x x
2 x x x x
3 x x x x x
4 x x x x
5 x x x
6 x x
Definition 2.1. A formal context K(G, M, I) consists
in two sets G and M, and a relation I among them. The
elements of G are called objects, while the elements
of M are called attributes. If an object g has a relation
I with a attribute m, this relationship can be expressed
by gIm or (g, m) ∈ I. This can be interpreted as “ob-
ject g has attribute m”.
Definition 2.2. For a set A ⊆ G of objects, it is defined
A
0
:= {m ∈ M|gIm ∀g ∈ A} (1)
as a set of common attributes to the objects in A.
In correspondence, to the set B ⊆ M of attributes, it is
defined
B
0
:= {g ∈ G|gIm ∀m ∈ B} (2)
as the set of common objects to the attributes in B.
Definition 2.3. A Formal Concept is a pair (A, B),
where A ⊆ G, B ⊆ M, A
0
= B e B
0
= A. A is called
of extension and B of intention. β(G, M, I) defines all
the concepts of the context (A, B).
2.2 Search Space
Definition 2.4. Formally, the search space of con-
cepts, or search space, is defined as the set formed by
all subsets of attributes and objects of a formal con-
text, which can or not give origin to formal concepts.
Definition 2.5. The set of attributes M of
a formal context K(G, M, I), is formed by
{a
i+1
, a
i+2
, . . . , a
i
, . . . , a
m−1
, a
m
}. Given a attribute
a
i
∈ M, the set F
a
i
is denominated closed set of a
i
,
and can be defined by
F
a
i
= {a
j
∈ M, ∀i < j ≤ m} (3)
For example, the closed set of the attribute a
m−1
is
{a
m−1
, a
m
}. For the attribute a
m
corresponds the null
set.
Definition 2.6. An attribute is joined to all subsets of
its respective closed set to form new sets. These new
sets are elements of a search subspace denominated
search subspace of an attribute (F3S) (Fu and Nguifo,
2003).
For example, the search subspace of the at-
tribute a
m−2
is defined by: {a
m−2
}, {a
m−2
, a
m−1
},
{a
m−2
, a
m
}, {a
m−2
, a
m−1
, a
m
}. That is, by all subsets
that include the attribute a
m−2
.
Based on the definition statement 2.5, note that the
size of the closed set of an attribute is well defined,
that is, the closed set itself will have no more than
m − i attributes. Thus, as the search subspace of at-
tributes is defined as the union of the attribute with all
the elements of its respective closed set, the size of a
subspace is defined by
|F3S
a
i
| = 2
m−i
f or 1 ≤ i ≤ m (4)
Therefore, the size of the search space of at-
tributes, that is, the set of all search subspaces of at-
tributes can be expressed as
|F3S| =
m
∑
i=1
|F3S
a
i
| (5)
3 RELATED WORKS
An important contribution for the Formal Concept
analysis field is presented in (Qi et al., 2004), where
the authors propose a new distributed algorithm for
formal concepts extraction through the search space
partitioning of the concepts. In that work, an approach
for validation of the subspaces, that is, of the sub-
sets that have more possibility of generating formal
concepts, was presented. Besides, the distributed pro-
posal presents a polynomial complexity order.
Therefore, in that work, only the mathemati-
cal formalism is presented, what makes it little im-
pactable from the practicable aspect, since it does not
present the experimental results of the proposed ap-
proach.
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
106

In (Fu and Nguifo, 2003), an algorithm to obtain
the concepts from search spaces is also presented. Al-
though, in that proposal, redundant attributes are re-
moved from input formal context before the stage of
generation of partitions, in order to diminish the ef-
fort of the algorithm for extracting the formal con-
cepts. Another important characteristic to be high-
lighted about this approach is that it uses the NextClo-
sure algorithm (Carpineto and Romano, 2004) to ob-
tain the formal concepts, and it does not take the
workload balance into consideration.
The authors conclude, through experimental re-
sults, that as a consequence of the usage of the
NextClosure algorithm to obtain the concepts, the
distributed proposal is able to deal with high-
dimensional contexts. However due to the non bal-
ancing of the workloads the algorithm can present
strong performance variations depending of the cho-
sen load factor (i.e. DP).
In (Hu et al., 2007), a partitioning approach for
the formal context is presented, what makes it differ
from the works mentioned before, since the context
is horizontally or vertically divided, in order to obtain
subcontexts. Obtained these subcontexts, the subcon-
cepts are then extracted and joined through a specific
operator, with the objective to find the final formal
concepts set. In (yun Li et al., 2003), all the mathe-
matical formalism necessary to the generation of for-
mal concepts in distributed systems is presented, en-
suring its viability.
In this work, a distributed solution to obtain the
formal concept from high dimensional formal con-
texts, referring to number of objects and high density,
is proposed. As a strategy for the distributed solution,
the proposal of the search space (Qi et al., 2004) will
be considered.
4 DEVELOPMENT AND
EVALUATION
METHODOLOGY
In order to obtain an experimental scenario more re-
liable to evaluate the proposed algorithm, the tool
SCGaz (Rimsa et al., 2009) was used to generate all
contexts. This tool is capable of generating random
formal contexts, and specifying the desired density
within a minimum and maximum value.
Table 2 shows the formal contexts used in this pa-
per.
Table 2: Contexts used in algorithm evaluation.
cxt no. of obj. no. of attrib. density
1 100 20 91%
2 200 20 90.5%
3 500 20 87.3%
4.1 Distributed Algorithm
The distributed algorithm based on search subspaces
is the fair division of the workload (Algorithm 1).
Thus, the search space of attributes between the dif-
ferent nodes makes up the cluster and the effective
union of subconcepts, extracted from these nodes in
a central node. Therefore, after all search subspaces
processing we obtain the final set of formal concepts
for the input context.
The algorithm to define the search subspaces of at-
tributes (i.e. Algorithm 1) is responsible for dividing
the search space between slave nodes from the clus-
ter. This task is performed in a central node, which
from here will be called node coordinator or master.
In this node, besides the effective division of attribute
search space, it is also performed the matching of sim-
ple subconcepts generated from the processing of at-
tribute search subspaces. This partitioning algorithm
is expressed by Algorithm 1.
ALGORITHM 1: Definition of partitions
INPUT: adopted block size (BS), amount
of attributes of the input context (M)
OUTPUT: search subspace of attributes
Begin
L = 0
for i = 0 to M do
L = L + C(M,i)
end for
for i = 0 to L/BS do
output (M, i*BS, BS)
end for
End.
As it can be seen, the search space of attributes
partitioning algorithm depends just on the number of
attributes (M) from the input formal context and the
maximum size (BS) of each partition. After the calcu-
lation of the size of the search space of attributes (L),
the algorithm provides the workload for each node.
Note that the partition definition has independence be-
tween the operations performed by the algorithm and
the formal context. Since in this phase, the relevant
information is only the input parameters M and BS,
mentioned earlier.
Another feature that deserves special attention is
the calculation of combinations to be performed on
the set of attributes of the Formal Context. Such fea-
ture limits the space of possible solutions to the pro-
A DISTRIBUTED ALGORITHM FOR FORMAL CONCEPTS PROCESSING BASED ON SEARCH SUBSPACES
107

posed algorithm. As we know, the calculation of com-
binations is an operation that has high computational
cost and tends to get worse exponentially with the in-
crease on input data. Thus, according to the following
section, the experiments were performed with con-
texts with relatively few attributes and many objects.
Regarding the calculation of the concepts (Algo-
rithm 2), the extraction of subconcepts is performed
by slave nodes. This is a fully independent task which
allows the execution of parallel partitions on each
node. Besides the fair division of the workload, we
can present an estimate of time to generate all Formal
Concepts, since the number of partitions is known and
the processing time of each node is very close to each
other.
The algorithm to obtain the subconcepts is de-
scribed by Algorithm 2.
ALGORITHM 2: Extraction of formal concepts
INPUT: Formal Context, partition offset,
block size
OUTPUT: formal concepts
Begin
r = -1
insidePartition = false
sum = 0
while not insidePartition do
r = r + 1
sum = sum + C(M, i)
if offset < sum then
insidePartition = true
end if
end while
i-th = C(M, r) - sum - offset
output (K, M, r, i-th, BS)
End.
In Algorithm 2, r denotes the subset of combina-
tions, o f f set expresses the offset within the search
space of attributes, that is, the number of combina-
tions already calculated and i-th is the ith combination
of the search space. The attainment of subconcepts is
preceded by the phase of discovery of the partition
beginning. In other words, from which subset (r) of
combinations the slave node has to begin the effec-
tive extraction of formal concepts. After calculating
the ith combination, the algorithm extracts the sub-
concepts that belong to the partition up to BS combi-
nations for the input context K.
Due to the behavior presented by Algorithm 2, it
reveals its parallel nature. The operations performed
on the input parameters are independent of any shared
structure, except the Formal Context that is not yet
modified by the algorithm.
The proposed algorithm is based on the calcula-
tion of combinations and on the set of attributes in
order to generate the search subspaces. Even though
one can consider a large number of steps, we show
that the strategy adopted to obtain a response is still
acceptable.
5 ANALYSIS OF THE
DISTRIBUTED ALGORITHM
This section presents the obtained results for the dis-
tributed algorithm, as well as the application architec-
ture and the computational environment used in the
experiments.
5.1 Application Architecture
Figure 1 presents the application architecture used
for the realization of our experiments. Note that
rectangles represent applications, arrows represent
the direction of program flow and diamonds are in-
put/output of data.
Figure 1: Diagram of the application architecture.
It is worh mentioning that the effective implemen-
tation of the distributed algorithm is the bigger rect-
angle (i.e. the one labeled Albatroz). Since Albatroz
is just a distributed application for the extraction of
formal concepts, other tools were used to create its
workloads, as well as give meaning to its outputs.
Finally, in Figure 2 is presented Albatroz’s se-
quence diagram.
5.2 Distributed Computational
Environment
The distributed computational environment used to
perform the experiments consists of a cluster based on
16 computers. Fifteen machines represent the slave
nodes, and one node represents the master. Table 3
shows the machine configurations used to process the
workloads. The master (coordinator node) is respon-
sible for distributing the workload and for joining the
concepts.
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
108

Figure 2: Diagram of the application architecture.
Table 3: Cluster configuration.
master slave
CPU model Intel Pentium IV Intel Core 2 Duo
Clock 3200.329MHz 2197.565MHz
Cache 1024KB 2048KB
CPU cores 1 2
RAM 2027.0859MB 1985.2773MB
O. S. GNU/Linux PelicanHPC
5.3 Experimental Results
As mentioned before, the formal contexts used were
generated in a random form, with the aim to obtain
a more reliable scenario for the tests. Besides, the
maximum density was considered for the workload,
since this value affects the algorithm performance to
extract the formal concepts (i.e. Algorithm 2).
All algorithms of the present work were imple-
mented in the Java programming language, since the
goal of this work is to present through experiements
the validity of the proposed distributed algorithm.
In order to measure the optimal size of the work-
load for the distributed algorithm, a sequential algo-
rithm for the extraction of concepts was used. This
sequential algorithm uses the search space approach
for the calculation of concepts and displays the execu-
tion time for the extraction of concepts of each subset
attributes, as well as, the time required to process all
theses subsets (cumulative total).
Having the time accumulated for the processing
of subsets of attributes, the size was selected, deemed
ideal for the workloads used in the experiments. Fig-
ure 4 shows the sum of execution time for processing
theses search subspaces for an input context with 100
objects and 20 attributes. It is noteworthy that it was
used only one Formal Context for the representation
of the curve, since the performance function always
shows the same behavior, no matter which dimension-
ality of the input context.
Based on this graphic, it is worth to note the
slightly non linear behavior of the performance func-
tion against the accumulation of subconcepts previ-
ously calculated, which shows the interdependence
between the effective time for the extraction of con-
cepts of the input context and the adopted block size.
Thus, in order to obtain a reasonable time for the pro-
cessing of partitions, we tried to select block sizes not
larger than a certain threshold (t) in the lower curve
of Figure 4. In addition to this, it can be seen that the
value of the derivative is smaller at the extremes of the
curve. Moreover, the lower region of the performance
function provides greater flow of concepts, since the
partition sizes in that region are smaller.
Figures 5, 6 and 7 present the results of execution
of the distributed algorithm for extraction of concepts
for 6, 11 and 16 computer nodes, respectively. The
main objective of these simulations is to verify the be-
havior of the distributed algorithm in the variation of
partitions size, as well as in the increase in the number
A DISTRIBUTED ALGORITHM FOR FORMAL CONCEPTS PROCESSING BASED ON SEARCH SUBSPACES
109

Figure 3: Graphic of the sequential algorithm.
Figure 4: Graphic of the sequential algorithm.
Figure 5: Extraction of concepts in 6 nodes.
of objects in the input context.
Note that, from the analysis of the experimental
results, the increase in the number of objects leads
to a linear increase in the execution time of the pro-
posed algorithm. In addition, the behavior of the per-
Figure 6: Extraction of concepts in 11 nodes.
Figure 7: Extraction of concepts in 16 nodes.
formance curve of the algorithm is closely related to
the amount of nodes used and the adopted block size
for the workloads.
For the graphic of Figure 5, varying the block
size of a Formal Context with 100 objects and 20 at-
tributes, there was a reduction of approximately 25%
in the runtime of the algorithm. This behavior also re-
peats for other formal contexts used in this test. How-
ever it is important to note here that mere reduction
in the block size for the workloads does not ensures a
decrease of the runtime of the algorithm. This can be
verified from the performance curve of an input con-
text with 500 objects, where the minimum time was
obtained with blocks of size 6196 (maximum thresh-
old).
In Figures 6 and 7, the increase in the number of
nodes for the extraction of formal concepts provides a
considerable stress in the measurement curve of per-
formance of the distributed algorithm. In Figures 5, 6
and 7, for a context with 100 objects and 20 attributes,
using blocks of size 3000 and 6196, the runtime of the
algorithm suffers noticeable increase when the num-
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
110
ber of nodes used is greater than 11. This behavior
also occurs for a context with 200 objects and 20 at-
tributes, where for blocks of size 3000, the increase
was approximately 7.73% in the runtime of the algo-
rithm, while for blocks of size 6196, the increase was
around 11.67%.
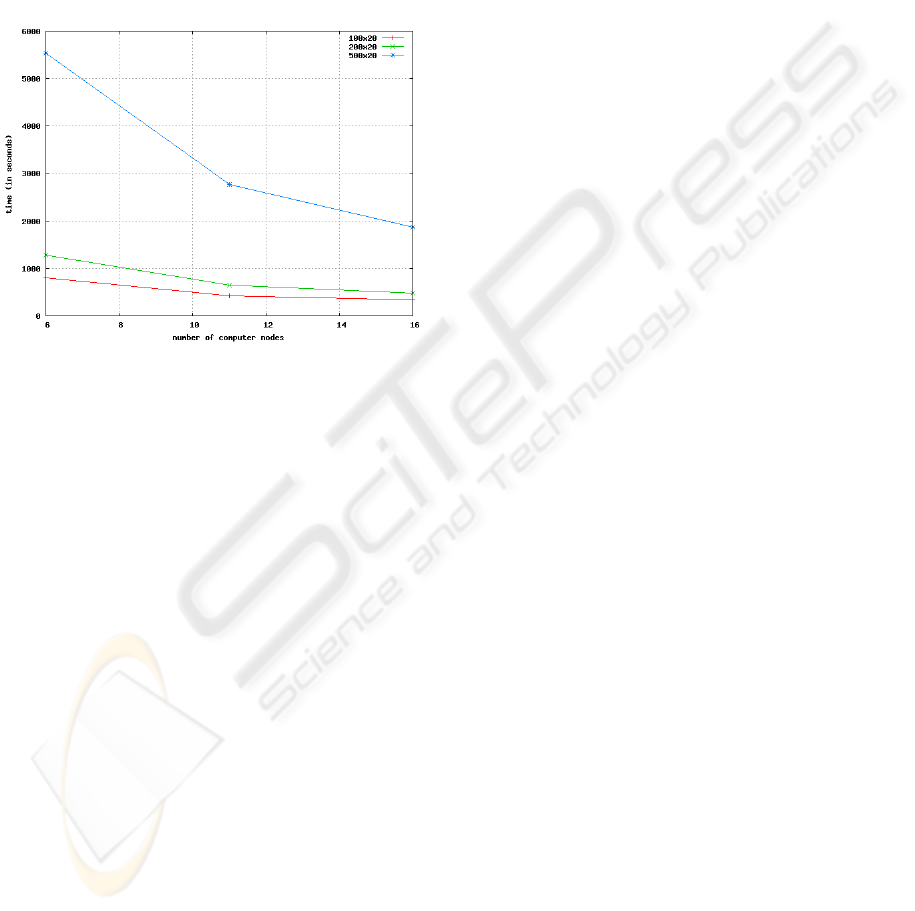
Figure 8 expresses the graphic of the relationship
between the number of nodes used for the processing
of formal contexts and the effective time to obtain all
formal concepts for blocks of size 1000.
Figure 8: BS = 1000.
Based on the graphic of Figure 8, it can be noted
that the performance of the distributed algorithm is
closely related to the amount of nodes used in the ex-
traction of concepts. Futhermore, it is worth mention-
ing that the performance curve tends to stabilize with
the gradual increase in the number of computers, due
to the overhead introduced by the use of a network.
It is also possible to observe that the reducing
in the runtime of the algorithm for an input context
with 100 objects and 20 attributes was approximately
57.88%, while for a context with 200 and 500 objects
the reductions were close to 62.85% and 66.23%, re-
spectively.
6 CONCLUSIONS
In this paper, a distributed approach for the extraction
of formal concepts for contexts with high density and
large number of objects was presented. It was veri-
fied that with this approach it is possible to determine
an estimative of the time required for the processing
of all concepts of a Formal Context, since the number
of interactions are known and the time for extraction
of concepts in the slave nodes are close to each other.
However, as shown in the experiments, the partition
size has some impact on the final performance of the
distributed algorithm. As a result, the values used for
the block size are not always the best ones. Conse-
quently, this may result in a substantial increase in the
runtime of the algorithm.
From this, it can be pointed for future works the
calculation of the best size for the workloads, as well
as test on Formal Context with huge number of ob-
jetcts (approximately 120,000). It is also important to
mention that through our preliminary studies it would
be possible to manipulate social network models char-
acterized through few attributes and large quantity of
objects.
ACKNOWLEDGMENTS
This research has received financial support of the
FAPEMIG through the PPMIII-67/09 Project and
CNPq, 471089/2008 Project.
REFERENCES
Carpineto, C. and Romano, G. (2004). Concept Data Anal-
ysis: Theory and Applications. John Wiley and Sons.
Fu, H. and Nguifo, E. (2003). Partitioning large data to scale
up lattice-based algorithm. Tools with Artificial Intel-
ligence, 2003. Proceedings. 15th IEEE International
Conference on, pages 537–541.
Ganter, B. (2002). Formal concepts analisys: algorithmic
aspects. TU Dresden, Germany, Tech. Report.
Ganter, B. and Wille, R. (1997). Formal Concept Analy-
sis: Mathematical Foundations. Springer-Verlag New
York, Inc., Secaucus, NJ, USA. Translator-Franzke,
C.
Hu, X., Wei, X., Wang, D., and Ii, P. (2007). A parallel
algorithm to construct concept lattice. Fuzzy Systems
and Knowledge Discovery, 2007. FSKD 2007. Fourth
International Conference on, 2:119–123.
Qi, H., Liu, D., Hu, C., Lu, M., and Zhao, L. (2004). A
parallel algorithm based on search space partition for
generating concepts. IEEE, (1):241–248.
Rimsa, A., Z
´
arate, L. E., and Song, M. A. J. (2009).
Handling large formal context using bdd – perspec-
tives and limitations. In Proceedings of the 7th In-
ternational Conference on Formal Concept Analysis
(ICFCA 2009), volume 5548 of LNCS/LNAI, pages
194–206, Darmstadt, Germany. Springer-Verlag.
yun Li, Liu, Z.-T., Shen, X.-J., Wu, Q., and Qiang, Y.
(2003). Theoretical research on the distributed con-
struction of concept lattices. In Machine Learning
and Cybernetics, 2003 International Conference on,
volume 1, pages 474–479 Vol.1.
A DISTRIBUTED ALGORITHM FOR FORMAL CONCEPTS PROCESSING BASED ON SEARCH SUBSPACES
111
