NEW APPROACHES TO ENTERPRISE COOPERATION

GENERATION AND MANAGEMENT

Jörg Lässig

International Computer Science Institute, 1947 Center Street, Suite 600, Berkeley, CA, U.S.A.

Ullrich Trommler

CBS Information Technologies, Curiestr. 3a, Chemnitz, Germany

Keywords:

Virtual enterprise, Enterprise cooperation generation and management, Enterprise resource planning, Decision

support, Supply chain management, Rich internet application, Collaboration, Replanning.

Abstract:

The paper considers the problem of task speciﬁc cooperation generation and management in a network of

small or medium sized enterprises. Such short-term cooperations are called Virtual Enterprices. So far this

problem has been discussed by several authors by applying different methods from artiﬁcial intelligence as

multi-agent systems, ant colony optimization, or genetic algorithms, and combinations of them. In this paper

we discuss this problem from a target oriented point of view and focus on the question how it can be modeled to

keep its complexity controllable by considering sequential, parallel, and non-combinatorial approaches. After

describing the implementation of a cooperation generation solution as rich internet application also solutions

for the management of such cooperations considering aspects as replanning are described.

1 INTRODUCTION

Besides the classical supply chain there are many oth-

er appearances of business cooperations as, e.g., joint

ventures, strategic alliances, and enterprise networks.

While the ﬁrst three types are long lasting coopera-

tions, according to Teich enterprise networks are very

dynamic by allowing to adopt new partners, to gain

new orders and to expand into new market segments

(Teich, 2002). Already Miles and Snow considered

dynamic networks which for the external observer or

customer can ideally act as one enterprise, and hence,

have been dubbed Virtual Enterprises (VE) (Miles and

Snow, 1984), see Figure 1. The concept is very close

to Shaw’s idea of Information-based manufacturing

(IbM) (Shaw and Fulkerson, 2001). In this work the

computer scientiﬁc aspects are emphasized.

In detail we consider the problem to gener-

ate cooperations especially consisting of small and

medium-sized enterprises to collaboratively solve a

given task, as e.g., to produce a machine tool. Ac-

cording to a request for such an product, the goal is to

choose eligible companies in a network according to

their competences and to compute different coopera-

tion scenarios automatically. As described by Martinz

Figure 1: Classiﬁcation of the virtual enterprise.

et al., in general there is a central resources pool, rep-

resenting the different companies in the network. The

starting point is a task request by a customer or net-

work participant (Martinez et al., 2001).

The next generation stage is to identify companies

which are eligible to process certain parts of the task

by matching competences and to inform them about

the task. This problem is not considered further in

this paper. If eligible companies are informed, the in-

350

Lässig J. and Trommler U. (2010).

NEW APPROACHES TO ENTERPRISE COOPERATION GENERATION AND MANAGEMENT.

In Proceedings of the 12th International Conference on Enterprise Information Systems - Artiﬁcial Intelligence and Decision Support Systems, pages

350-359

DOI: 10.5220/0002978203500359

 SciTePress

terested ones bid in some way on parts of the task and

an algorithm generates a cooperation solution to ful-

ﬁll the request by using the competencies of different

enterprises. Finally, the product is produced in the re-

quested number of items and delivered. This means

the process can be seen as a circle, starting with the

submission of a new task (from a customer) and end-

ing with the delivery of the product (to this customer).

As we will see, it is reasonable to specify tasks by

means of work packages with time constraints in be-

tween, so called precedences.

The described problem has already been ad-

dressed in research for about twenty years, and sev-

eral approaches have been described. However, due

to a set of intricate problems in this context no ulti-

mate solution is known and none of the proposed so-

lutions is used in practice so far; refer, e.g., to Teich

for a survey (Teich, 2002). One reason is that the task

to accomplish includes several interacting problems

combined with duration and time constraints, moni-

toring, replanning, or failure management.

Of central importance is the generation of feasible

candidate cooperation solutions, which requires the

assignment of speciﬁc parts of the task to companies

and calculating necessary logistics operations, costs,

and ﬁnishing times in this scenario. A crucial point

in this process is the restriction of the computational

complexity of the generation task, which is due to the

modeling of the task itself, the structure of bids, and

the design of the solution space. Depending on the

model, the computation can include solving complex

multi-criteria optimization problems with side con-

straints to ﬁnd groups of enterprises which ﬁt best to

a speciﬁc request. This paper considers particularly

this central cooperation generation problem.

First, we describe the problem to be solved in

more detail in the next section. Then, in Section 3,

different modeling scenarios are discussed, including

historical approaches. Particularly, some important

design aspects are worked out. Subsequently, in Sec-

tion 4, we focus on the browser-based implementa-

tion of a cooperation generation and control system

covering the features as discussed in the sections be-

fore. The system has been implemented complete-

ly browser-based by applying state of the art web-

technologies. Additionally, in Section 5, the coop-

eration management with questions as replanning is

outlined, before the paper is concluded in Section 6.

2 PROBLEM FORMULATION

A crucial part for this kind of problem is to ﬁnd a good

model. First, we restrict ourselves to a case where a

work piece from mechanical engineering has to be

produced, let’s say a cog wheel on a shaft. Sever-

al scenarios in literature now assume that this work

piece is available as CAD ﬁle, i.e., as 3D model with a

description of all features as described by Pratta et al.

(Pratta et al., 2005). This has the advantage that for

each feature the complete knowledge about the ma-

chines needed to produce the work piece is available.

For speciﬁc machines the time to produce it can be

calculated, at least in principle. This “complete” ap-

proach faces several problems in practice, as there are:

• All tasks must be available as complete CAD ﬁle,

which is not the case for small lots and small en-

terprises.

• The cooperation generation system would have to

be able to process all common CAD standards.

• The complete feature description of workpieces is

still a research problem.

• The number of combinatorial possible coopera-

tion scenarios becomes extremely high due to the

small granularity of subtasks and operations.

• Practically, it is in principle sometimes not pos-

sible to do each operation on another machine if

speciﬁc preciseness is necessary.

Therefore, we only look at a scenario where ﬁxed

work packages are suggested by the party issuing an

invitation to bid with precedence constraints in be-

tween. This is a scenario which can be described by a

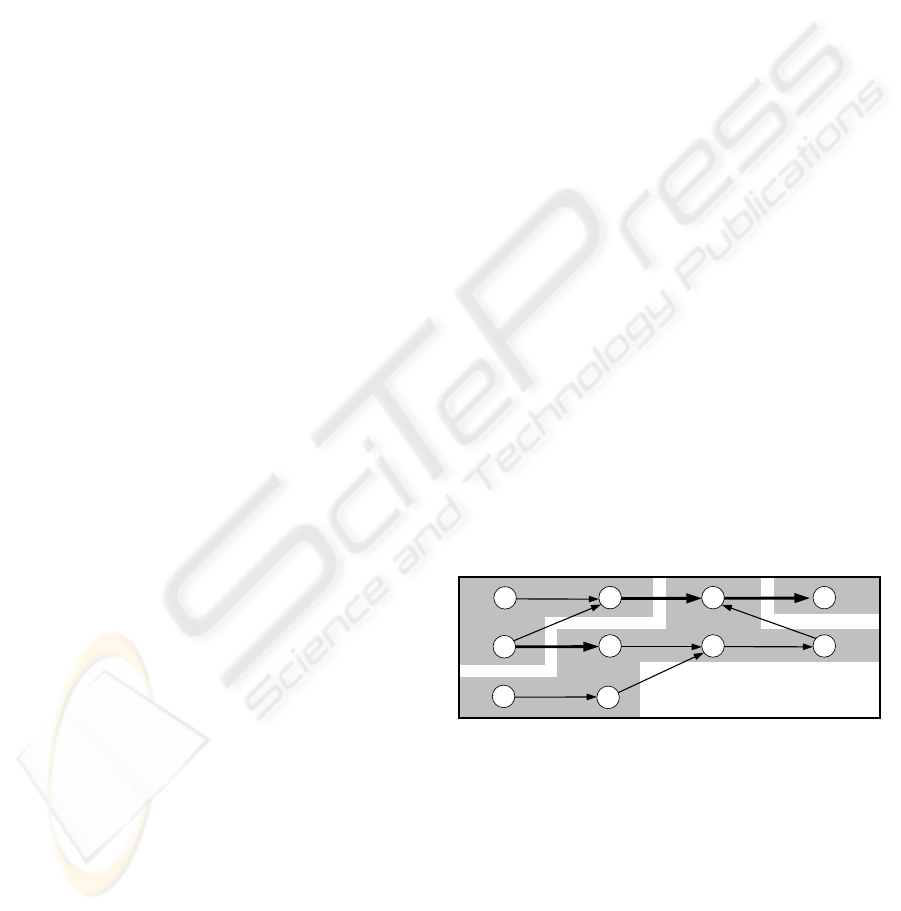
graph as shown in Figure 2. In the extreme case this

approach could be used to model all operations of the

work piece as work package, but as we will see, this

would be computationally difﬁcult to treat.

2 6

4 7 10

Figure 2: Task graph with precedences between work pack-

ages and three chosen bids (grey)

Consider that for each work package parameters

are available if a certain machine can process this

work package or not. Because a complete feature de-

scription of the operations in these work packages is

assumed to be not available in our scenario, this can

be done only with a certain probability, utilizing in-

complete information. This problem is not discussed

here further but Lässig describes how this can be real-

ized (Lässig, 2009). Here we just assume the follow-

ing situation:

NEW APPROACHES TO ENTERPRISE COOPERATION GENERATION AND MANAGEMENT

351

• There is a set C = {1, 2, . . . , C} of companies and

each company has a set of machines M (c), c ∈ C .

• There is a set of work packages w ∈ W .

• There is some mechanism to reason with high

probability which company can process a certain

work package.

Because this mechanism is probabilistic and because

the work packages are not described completely ma-

chine readable, it should be clear that human interac-

tion is necessary to decide if a certain work package

can ﬁnally be realized. To be able to do this, it is

necessary to have detailed information and technical

detail drawings available, of course. Further informa-

tion are assumed to be added in this phase as well,

e.g., the price for the service or time constraints. Fi-

nally, the company bids on a subset of work packages

adding also this information. This is the general set-

up, which is discussed now in different scenarios.

3 MODELING DECISIONS AND

CENTRAL ASPECTS

So far we have a set of work packages and a set of

bids on them by the companies. It is open, how ex-

actly bids should be structured, which further infor-

mation should be provided by the bidders and how

the system uses these information to generate cooper-

ation solutions. A cooperation solution is in our case

an assignment of companies to work packages, i.e.,

for each work package there is a company to process

it. Further, different cooperations should be compa-

rable by reasonable objectives. Part of the objective

function should be at least the occuring costs (includ-

ing logistics between participants) and the ﬁnishing

time of the cooperation. Quality or robustness are of-

ten mentioned as possible further measures.

3.1 Sequential Assignment

In (Teich, 2002) a sequential bidding scenario is de-

scribed. The work packages as shown in Figure 2 can

be topologically sorted (Corman et al., 2001) and then

starting with the topologically last work package all

companies which are able to process the work pack-

age in principle are asked to bid by submitting a price

and a start time of this work package. If n companies

are bidding then the search tree has n branches in this

stage and in each branch of the search tree, the start

time of the next work package is known. Now in each

search branch again all companies which are able to

process the previous work package(s) are asked to bid.

In each of these cases also the logistics time and cost

can be calculated. Of course this scenario has disad-

vantages:

• The search tree gets exponentially large.

• Each company has to bid many times and in dif-

ferent stages and branches of the search if more

than one work packages are of interest.

While the ﬁrst problem causes dramatic running times

for instances with many work packages and many bid-

ders, the second problem rules out human interaction

in the bidding process, i.e., in this scenario only soft-

ware can bid. This again is only possible if any infor-

mation about the task, the machines, and the schedul-

ing in the company which bids is completely avail-

able. As described above, this is in practise often not

the case.

3.2 Parallel Assignment

From the previous section we have seen that it is desir-

able to ﬁnd a scenario where the number of bids is low

for each company in order to reduce the workload and

to permit manual bidding. Ideally, each company sub-

mits a set of work packages together with a price and

some timing constraints, which has been proposed by

(Lässig et al., 2007). Let’s leave out the complication

due to the necessary termination of the work packages

for a moment, which can be realized by a graph tech-

nique called important paths, described, e.g. in (Läs-

sig, 2007). If companies submit sets of work pack-

ages, we face essentially a combinatorial problem as

described in the following:

Deﬁnition 1 (Work Package Allocation). For a set

of bidding companies C = {1, 2, . . . , C} and a set of

work packages W = {1, 2, . . . , W }, with P (W ) de-

noting the power set of W , the variables x

i, j

are de-

ﬁned for bids b

i, j

∈ B

and B

⊆ P (W ) by

i, j



1 | if bidder i gets assigned bid b

i, j

0 | otherwise

and form a work package allocation x. Here i =

1, 2, . . . , C is the index for the bidding company and

j = 1, 2, . . . , B

is necessary to distinct between bids

of the same company, where B

is the cardinality of

the bid set B

of company i, which is a set of sub-

sets of items, the company i is bidding for. Each item

i, j

∈ B

forms a single bid.

An allocation x is called feasible if work packages

are allocated at most once, represented by the con-

straints

∑

i∈C

∑

i, j

∈B

i, j

∩{k}6=

i, j

≤ 1, k = 1, 2, . . . , W . (1)

ICEIS 2010 - 12th International Conference on Enterprise Information Systems

352

A feasible allocation x is called complete if (1) de-

mands equality to one.

The Weighted Exact Cover Problem (WECP) is

then deﬁned as follows:

Deﬁnition 2 (WECP). Given a setup as deﬁned in

Deﬁnition 1 and, additionally, costs c

i, j

a company

i ∈ C is declaring to charge for processing the work

packages in b

i, j

∈ B

, the WECP is deﬁned to ask for

x ∈ argmin







∑

i∈C

∑

i, j

∈B

i, j

· x

i, j



x is complete







Different algorithmic approaches to this problem and

also a generalized version, which integrates further

objectives besides costs, have been investigated be-

sides many optimization aspects for questions of

search organization (Lässig, 2009).

Algorithm 1 introduces the basic template to solve

the problem WECP, where the costs of a set X ⊆ B of

all given bids with

b∈X

b ⊆ W are deﬁned as

c(X ) =

∑

i, j

∈X

i, j

. (2)

The algorithm implements a recursive search. The

lines 1–4 describe terminating conditions of the re-

cursion. In line 5 a branching decision is calculated

which can, e.g., be a decision that some bid is taken

or not taken or a decision which bid is used to cover

a speciﬁc work package. The search is then contin-

ued in D

different branches of the tree. The function

next_tuple partitions the set of working packages and

bids according to the branching decision.

Algorithm 1. Basic_search(W , B, X

, X

bsf

Require: work packages W , bids B with price c

i, j

for b

i, j

∈ B, input set X

, best so far solution X

bsf

Ensure: set

X of bids, covering W exactly with

price c(

X ) = min{

∑

i, j

∈X

i, j

| x(X ) is complete}

1: if (W =

0) then

2: return argmin{c(X

), c(X

bsf

)}

3: if (B =

0) then

4: return X

bsf

5: D

← get_branching_decision(W , B, X

, X

bsf

)

6: for i ← 1 to r

7: (W

(i)

, B

(i)

, X

(i)

) ← next_tuple(B, X

, D

, i)

8: X

bsf

← basic_search(W

(i)

, B

(i)

, X

(i)

, X

bsf

)

9: return X

bsf

Although this kind of search algorithms can have an

exponential running time in the worst case, theoreti-

cal investigations and also experimental studies show,

that the problem keeps computational tractable under

reasonable assumptions. In the algorithm there are

two degrees of freedom left, indicated by the func-

tions get_branching_decision and next_tuple, which give

room for many improvements and strategies to accel-

erate the algorithm by orders of magnitude.

Examples of improvements to accelerate the two

functions above are for instance different branching

strategies (branch on bid, branch on work package,

generalized branching, etc.), bid ordering strategies,

combinatorial pruning rules, and the application of

heuristic pruning functions, known from other appli-

cations as the Winner Determination Problem (Sand-

holm, 2002). Worst case results show that the number

of possible solutions for the problem WECP is poly-

nomial in the number of bids but exponential in the

number of work packages.

100

150

200

250

300

350

400

450

500

100

150

200

250

300

350

400

450

500

Expected Number of Exact Cover Solutions E(W,B)

400

300

200

100

Number of working packages W

Number of bids B

Figure 3: Expected number of exact cover solutions.

The plot in Figure 3 shows the expected number of

solutions (average case) for given numbers B of bids

and W work packages, calculated by the exact count-

ing function

(W, B) =

∑

i=1





− 1)

−i

i−1

∑

j=0

(−1)





(i − j)

which has been developed to investigate performance

issues and which scales well with the running time

of solvers as Algorithm 1 (Lässig, 2009). It shows

that the expected number of solutions is moderate for

moderate input sizes W and B. It turns out that this is a

very good indicator for the running time of implemen-

tations as Algorithm 1, applied to solve this problem,

see Figure 4. This means the equation above turns out

to be a good model for the running time.

As one can see in the visualization, if the number

of work packages is increasing, the expectation to re-

ceive at least one possible solution is decreasing for a

constant number of bids. Therefore, in practice it is

not sufﬁcient to search only for solutions of a given

problem – further strategies are necessary.

NEW APPROACHES TO ENTERPRISE COOPERATION GENERATION AND MANAGEMENT

353

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

100

200

300

400

500

600

700

800

900

1000

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

Expected Number of Exact Cover Solutions E(W,B)

1.5

0.5

Number of working packages W

Number of bids B

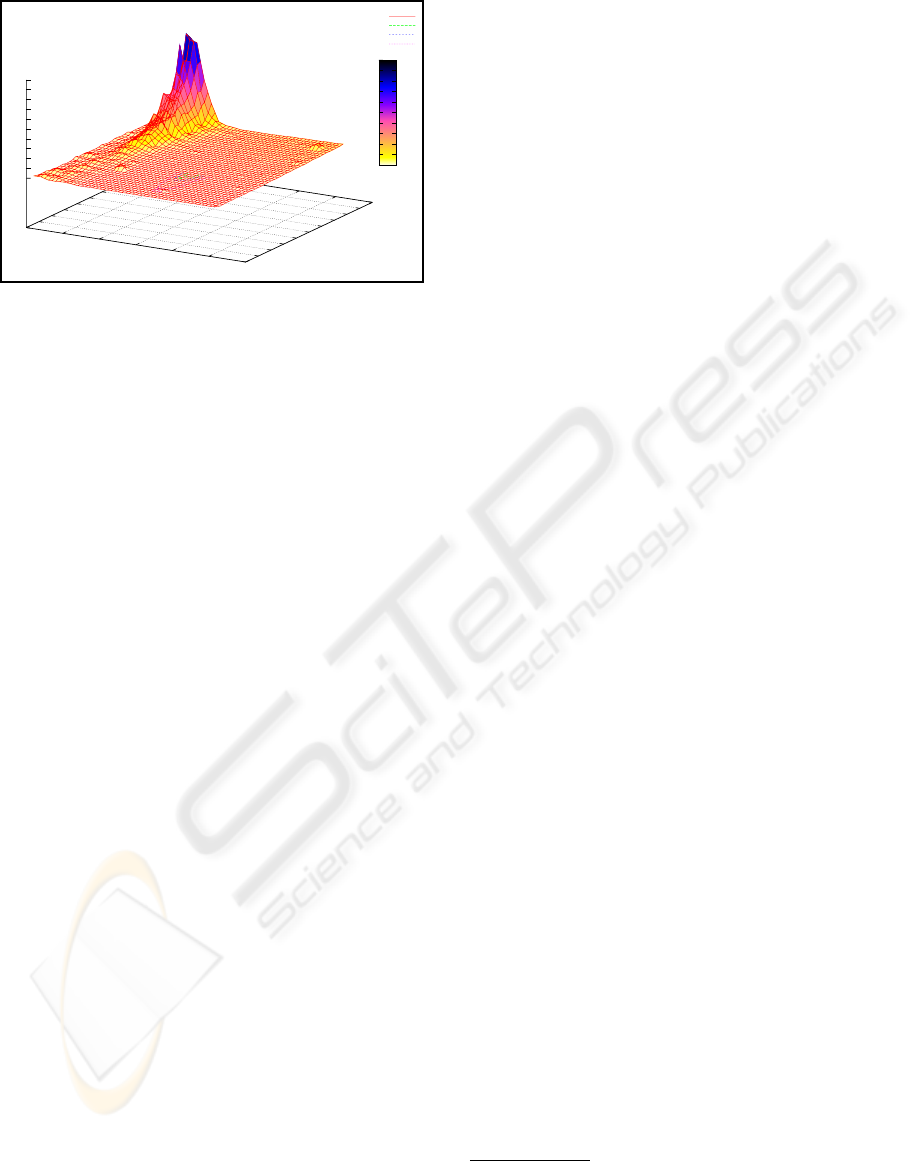
Figure 4: Experimental running time for the solution.

Actually, it turns out that the scenario is control-

lable if two special cases are carefully taken into ac-

count:

• the worst case in terms of the number of solutions,

which can be very large, is treated in some way,

• the case that no solution is found is treated in

some way, because this may happen even if many

bids are available.

The second problem can be handled by providing pos-

sible completing bids for potential bidders, i.e., bids

which complete partial solutions to exact cover solu-

tions or at least towards them. These can be calculat-

ed in the last recursion step. Further, the strategy to

handle the ﬁrst problem is to not consider all possi-

ble solutions if there are too many (by using heuris-

tics). Further constraints as the termination of the so-

lution according to given timing parameters and the

search for an optimal solution in an multi-objective

scenario complicate the search. Hence, a simpler ap-

proach seems to be desirable. Major motivations are

• the algorithmically quite elaborate handling of the

combinatorial bidding situation combined with

multiple objectives and timing constraints,

• the fact that many bits are ruled out and do not

contribute to the set of solutions only for combi-

natorial reasons.

3.3 Removing Combinatorics

A straightforward way to simplify the scenario is that

each company bids non-combinatorial, which means

independently on different work packages it is able to

process – with separate prices and time constraints,

which we left out so far but which are introduced be-

low. Of course this has disadvantages because now

the companies are not able to express that they are on-

ly willing to bid on certain groups of work packages

but, it can have advantages for reducing the complex-

ity of the scenario. We also leave out logistics here.

The central problem now is that the number of

possible solutions is much larger not only in the worst

case but in any case for a given number of bids and

work packages, i.e., if B(w

) is the number of bids on

work package w

and W the number of work pack-

ages, then the overall number of different solutions is

S =

∏

i=1

B(w

) .

This yields 2

if there are exactly two bids for each

work package, which means exponential many solu-

tions in the number of work packages.

However, in the case of no further constraints, i.e.,

each bid can be combined with each other bid on oth-

er work packages, the most cost-efﬁcient solution can

be found trivially by taking the cheapest bid for each

work package. Unfortunately, in practise cost is im-

portant but other objectives as time for the realization

of a certain task as well.

Consider the following simple scenario:

• for each bid b

i, j

∈ B, which includes only one

speciﬁc work package, besides the cost c

i, j

also

the duration d

i, j

to complete the work packages is

given

• there is an overall earliest start time t

and an lat-

est end time t

and only for this time frame the

durations are guaranteed by the bidder,

• there are no further objectives besides cost and

time.

Now it is easily possible to ﬁnd the solution with

the earliest completion time: Just topologically sort

the work packages in the sorting which is given

by the task graph (Figure 2) and use the classical

CPM/PERT approach (with equivalent best-case and

worst-case times for the work packages) to ﬁnd the

completion time if for each work package the bid with

the smallest duration is taken into the solution.

To ﬁnd the cheapest solution is now already more

involved because just taking for each work package

the bid b

i, j

with smallest cost value c

i, j

does not nec-

essarily give a feasible solution because the duration

could be larger than the time period t

− t

. It gets

even more involved if a tradeoff between several ob-

jectives has to be found. From a theoretical point of

view, it would be the best to present all Pareto-optimal

solutions to the user, i.e., solutions where for each of

Let us consider the case that this duration is the real

working time, i.e., we do not consider weekends or work-

ing times of the companies in this scenario. In a practical

implementation this has to be taken into account.

ICEIS 2010 - 12th International Conference on Enterprise Information Systems

354

them no other solution exists which is better in each

of the different objectives. The problem is that there

can be exponentially many Pareto-optimal solutions

for some problems and this is also the case for our

problem, as the following example shows.

Example. Consider a task which consists of n

work packages which are labeled with the num-

bers 1, 2, . . . , n. Further there are precedence con-

straints between the work packages i and i + 1 for

i = 1, 2, . . . , n − 1. This means we have a chain of

work packages. Now consider that there are two bids

i,1

and b

i,2

for each work package i, where the du-

ration for each bid b

i,1

is d

i,1

= 1; for b

i,2

we have

i,2

= 2. For the cost we have exactly the opposite

situation: c

i,1

= 2 and c

i,2

= 1. Now, there are 2

solutions but all of these solutions are Pareto-optimal

because for each solution there is no other solution

with lower cost and shorter duration.

Approaches as the weighted linear sum method

are obvious and intuitive ways to prevent the neces-

sity to return all of these solutions. In a minimization

context the returned solution is formally described by

min f (x) =

∑

i=1

· f

(x)

subject to g(x) ≤ 0, h(x) = 0 .

The constraints are not of interest in our case. Nev-

ertheless, this method applied without additional con-

cepts has a major drawback - it cannot discover so-

lutions hidden in concave regions of the Pareto-front.

Other approaches are the Distance to a Reference Ob-

jective Method, the ε-Constraint Method or the Cor-

ley Method, as e.g., described by Coello and Lamont

(Coello and Lamont, 2004).

More intuitively to handle are methods which in-

teract with the user. Here we choose the following

approach: First only the fastest possible solution is

computed and visualized for the user as described

above, just by using the obvious topological sorting

approach. Say this solution has the overall duration

d. Now the user knows the cost of the most time efﬁ-

cient solution. If he is only interested in this solution,

he will choose it and the task is done. If this is not the

case, the user is asked to tell us how much (planned)

time more he is willing to spend if the costs can be

reduced (at this point it is unclear how much cost can

be saved). Now, given additional duration d

add

, the

algorithm has to come up with a solution with cost as

low as possible but planned duration at most d + d

add

Interestingly, this is still a difﬁcult problem. That

it is indeed NP-hard can be seen from a speciﬁc exam-

ple. Consider n work packages in a chain as described

in the example above and also with two different bids

for each work package (the cost of the bids is arbi-

trary, but ﬁxed). Now consider the solution with the

shortest duration is found and d

add

is given by the us-

er as described. We assume without loss of generality

that there are only non-dominating bids, i.e., bits with

shorter duration have higher costs.

Now the following Knapsack problem can be de-

ﬁned: There are n (number of work packages) ob-

jects in the knapsack. The utility value of the object

for work package i is equivalent to the absolute val-

ue of the cost difference of the two bids for i (where

the more expensive bid should be assigned because

we have currently the solution with shortest duration).

The cost value for object i in the knapsack is the ab-

solute value of the duration difference of the two bids

for i. Now the problem is to ﬁnd the set of objects with

largest possible utility value where the cost threshold

is d

add

. Because the problem is just a special case of

the original setup, this in turn must be NP-hard.

For more general task graphs the problem cannot

be reduced to a knapsack problem but using standard

optimization heuristics it is still possible to get near

optimal solutions in most cases. Interesting speciﬁc

tractable cases exist if the structure of the task graph

is restricted to a tree. Then it is possible to either han-

dle combinatorial settings of connected bids in poly-

nomial time if only one objective has to be optimized

(Lässig, 2009) or to optimize according to different

objectives as time and cost including logistics if the

time scale is restricted to ﬁxed intervals as hours or

days, which is a reasonable assumption in the given

setting. To conclude, it is interesting to see that also

very relaxed versions of the cooperation generation

problem are still computationally hard to treat.

Comparing the three approaches, advantages and

disadvantages can be identiﬁed for each of them and

there is no deﬁnite “winner”. For practical realiza-

tion we ruled out the sequential approach but decided

to realize a system which supports combinatorial and

non-combinatorial setups.

4 IMPLEMENTATION

A solution which supports cooperation generation as

described has been implemented as web-application.

The implementation of the system is especially based

on modern internet technologies as AJAX, remoting,

and web services and can be completely controlled

from the browser. Besides cooperation generation and

control (monitoring facilities, communication) fur-

ther functionalities have been integrated in the sys-

tem, such as facilities for visualization, failure man-

agement, up to social networking on enterprise level.

NEW APPROACHES TO ENTERPRISE COOPERATION GENERATION AND MANAGEMENT

355

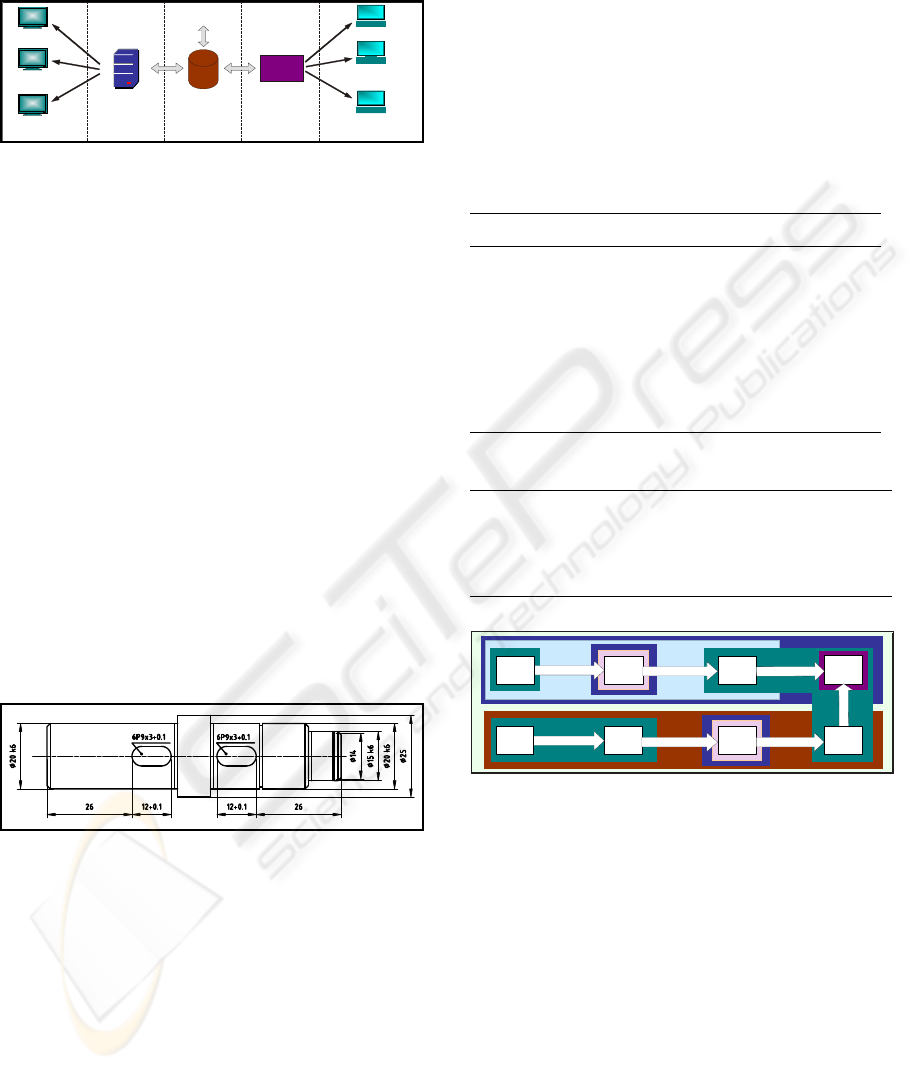
Figure 5 gives an overview on the ﬁve layer system

architecture.

Internet

Explorer

Firefox

Opera

Layer 1

MS IIS 7

Webserver

Database

MS SQL-Server

Win-Process

Load Balancer

Compute Client 1

Compute Client 2

Layer 5

Compute Client n

Layer 2 Layer 3 Layer 4

ERP/ PPS

WCF

CLR

Trigger

Figure 5: System-layout.

For the web-frontend the .NET framework and es-

pecially ASP.NET have been used. To realize com-

putationally intensive tasks like the cooperation gen-

eration as described and the termination of the work

packages, several compute clients are accessible by

a load balancer, which itself communicates with the

data base system. New computation tasks are started

by CLR triggers. The planning and monitoring facil-

ities especially visualize the planned tasks in the dif-

ferent companies directly in the web-interface, which

is shown in the Figures 8 and 9. Further information

about the system and its implementation can be found

in (Lässig, 2009). In the following sections the appli-

cation as described above is clariﬁed by an exemplary

cooperation task in a combinatorial auction scenario.

4.1 Example Workpiece

As example we consider the scenario that there is a

gear box assembly to be produced, consisting of a

shaft and a cogwheel, compare Figure 6.

Figure 6: Engineering detail drawing of the shaft.

To manufacture the workpiece, several production

methods have to be used. The process steps for the

production of the shaft are divided into three work

packages, which are not further speciﬁed here. The

process steps for the production of the cogwheel are

divided into four work packages. Afterwards the as-

sembling of both components follows. This speciﬁes

the last work package –WP8– for the ﬁnal assembly

of the shaft and the cogwheel. The work packages

with precedence constraints are shown in Figure 7.

Nine ﬁctitious companies, which represent the

acting parties in the system, are equipped with dif-

ferent skills and competence proﬁles and bid in our

example. In a heuristic preselection step, as described

above, the system chooses companies which are able

to realize at least one of the work packages. These

companies receive a message from the system’s inter-

nal messaging system and are requested to bid. In the

considered scenario they bid on the work packages as

shown in the second column of Table 1. The bidding

situation is also visualized by the colored regions in

Figure 7, where the different bids are indicated by the

different colors.

Table 1: Bidding situation.

Enterprise Bidding on work packages

ASU WP1, WP2, WP3

FEMA WP4, WP5, WP6, WP7

Sotec WP8

PraeTec WP1-WP8 (all packages)

RTC WP1, WP2, WP3, WP8

Seifert WP2, WP6

Interarms WP6

ExeMa WP1, WP3, WP4, WP5, WP7, WP8

GlobaMeta WP2

Table 2: Expected solution scenarios.

Variant 1 ASU, FEMA and Sotec cooperate

Variant 2 Only PraeTec participates

Variant 3 FEMA and RTC in the cooperation

Variant 4 Only Interarms, ExeMa and GlobaMeta

Variant 5 Seifert and ExeMa participate

WP5

WP8

WP4 WP6

WP3WP2

WP1

WP7

Figure 7: Task graph with bids.

4.2 Cooperation Solution

From the bidding situation as described by Table 1

one can easily obtain ﬁve different cooperation sce-

narios. The variants as indicated in Table 2 are as

expected also found by the system. In Figure 8 these

solutions are visualized and ranked by different anno-

tated objective function values. We apologize that the

screenshots are in German, but the system language is

currently German.

Figure 8 visualizes also one of the solutions in de-

tail, i.e., the solution including ExeMa and Seifert.

The system provides also a detailed view of each so-

lution including the Gantt charts as introduced in Fig-

ure 9 with the termination of the work packages for

all available solutions.

ICEIS 2010 - 12th International Conference on Enterprise Information Systems

356

Figure 8: Detailed view of a solution.

Figure 9: Gantt view of a solution.

5 COOPERATION PHASE

After the planning phase is ﬁnished, a task is pro-

cessed by the different participants. In this realization

phase other questions are important than the ones pre-

viously discussed, covering the management of this

realization process, communication between collabo-

rators, progress visualization, and if necessary replan-

ning. Within the forthcoming section monitoring and

failure management approaches are introduced.

5.1 Two-chart Approach

Introducing a monitoring setup with two GANTT

charts –one with the originally planned scenario and

one with the prognostic development based on the

current information– has many advantages compared

to other approaches:

• Each participant can immediately obtain sufﬁcient

information about the state and prognostic de-

velopment of the cooperation, without additional

workload caused by failure messages or message

propagation to succeeding participants.

• Different prognostic measures, such as the prog-

nostic delay of all work packages and the com-

plete cooperation, can be obtained directly from

a visualization, which includes all available infor-

mation on one screen.

• Reasons for different delays can be clearly ar-

ranged and are accessible.

• It is possible to support different reporting levels

of the participants (see below).

A disadvantage of this approach is that if the two

GANTT charts become too different, the current plan-

ning situation has to be updated to be still useful. The

party issuing the invitation to bid should decide if a

replanning is necessary.

Replanning is just a special case of sequential

planning. In general, all work packages are ordered

topologically considering the precedences of the co-

operation. Especially in the case of replanning, the

cooperation is already in progress and a few work

packages may be already ﬁnished. For replanning on-

ly unﬁnished work packages have to be considered.

Further, all work packages which are not delayed in

the prognostic GANTT chart are initially not consid-

ered. One starts replanning with the topologically ﬁrst

work packages, which are delayed. The participants,

who process these work packages, are asked for a new

prospective end time of these work packages and also

of succeeding work packages which are executed by

them as well within the same bid. Then the companies

which process the in the topological order succeeding

work packages are asked sequentially, until the last

work packages in the topological sorting are reached.

An interesting question is how to provide some

decision support if replanning is necessary in a cer-

tain situation or not. In any case this should be real-

ized as an assistance system, i.e., the ﬁnal replanning

decision should be made by the party issuing the invi-

tation to bid.

5.2 Necessary Information

To provide decision support, different input data is

needed, e.g. the following items:

• Information about the currently planned start and

end times of each work package,

• Information about the current progress d(i) of

each work package i = 1, 2, . . . , W (automatic re-

porting) or information about the work package

status (planned, in execution, ﬁnished) or at least

information about the progress state of the work

package (in time, borderline, delayed); (the level

borderline is deﬁned as a delay which is below x

NEW APPROACHES TO ENTERPRISE COOPERATION GENERATION AND MANAGEMENT

357

percent of the duration, while the status delayed is

interpreted as a delay of more than x percent),

• Available user-estimated delays t

(i) of the end

time of work packages i = 1, 2, . . . , W caused by

failures in the own company as machine break-

down or lack of resources,

• The ratio between the remaining time of the coop-

eration and the overall time of the cooperation,

• The ratio between the delay of a company and the

overall working time of the succeeding company,

• The factor mobility (replaceable, moderate re-

placeable, difﬁcult to replace, unreplaceable) of

succeeding production factors.

Independently from the replanning decision, a prog-

nostic GANTT chart about the cooperation based on

this data can of course be visualized as described. To

integrate these information also in the current plan-

ning, different ways to implement a possible escala-

tion strategy for replanning are possible, but this is

not discussed in detail here. In the next section we

describe disadvantages of the two-chart approach and

motivate continuous replanning.

5.3 Disadvantages of the Approach

Besides strong advantages, the mentioned overall de-

sign of a monitoring and failure management system,

based on two different GANTT charts with explicit re-

planning events, is quite involved and has also a few

disadvantages, as there are:

The ﬁrst and most obvious is that he monitor-

ing screen visualizes two different scenarios which

may be difﬁcult to explain to potential users in prac-

tice. Further, a GANTT chart including information

as prognostic end times is appealing, but the progress

d(w) from a company’s internal systems is not in any

case correct and reliable: If a machine produces items

of a certain good one after another, this is reported by

the MDE system of the machine and hence also to the

ERP-system (in case this infrastructure is existent). In

this case it is simple to get reliable measures about the

progress. If e.g. 300 of 1000 items are already pro-

duced, the progress must be about 30 percent. For

other operations as annealing this has to be calculat-

ed by another equation because all items are more or

less produced in parallel. If all items are in the an-

nealing process and 4 hours of 10 hours annealing are

over, then the progress state is obviously about 40 per-

cent, but no item has been ﬁnished yet. Other cases

can be constructed easily. Applying manual report-

ing, this information is not that exact. Furthermore, it

is unclear if the processing rate can be increased by

company internal changes - e.g., by enabling another

machine to make up for lost time, so that the deadline

can still be met. Hence, using this information di-

rectly to calculate a prognostic GANTT chart may not

always be realistic and cause problems if a replanning

decision is based on wrong information.

Another disadvantage is that there must be some-

body to decide if replanning should be executed or

not, which is additional workload. Apart from that,

replanning itself is an additional workload for the par-

ticipants of the cooperation. As last disadvantage we

would like to mention the discontinuity of the overall

production process caused by a division into periods

between replanning events. These problems caused

a rethinking on the monitoring and replanning sce-

nario as described above. An elegant setup which in-

cludes many of the mentioned advantages but ruling

out many of the mentioned disadvantages is continu-

ous replanning, introduced in the following section.

5.4 Continuous Replanning

In the continuous replanning approach, only one

GANTT chart is used. Progress information about

work packages and prognostic end times are only re-

ported to other users directly in this GANTT chart: If

a work package is in state borderline, it is highlight-

ed with an orange frame, if it is delayed with a red

frame, otherwise with a green frame. The prognostic

end time t

)

prog

is only reported in a context menu.

Now we explain how periodic replanning as de-

scribed can be eliminated. As mentioned, failures and

delays can be reported. In the previous approach,

this information had only informative character but

has been visualized in the prognostic GANTT chart.

Additionally, current failures and breakdowns are re-

ported in a special table current failures, annotated

with additional information, such as the affected work

package, the reason of the failure and the new expect-

ed end time. It is not too difﬁcult to integrate infor-

mation about delays or other time changes in a prog-

nostic GANTT chart. To integrate this information in

a valid planning chart, further knowledge about the

effect on the following work packages is demanded

because in the prognostic chart the new times of suc-

ceeding work packages are just extrapolated, which is

not reliable enough for actual planning.

The idea of continuous replanning is now to soften

this strict concept: If a work package is delayed, the

start time of the succeeding work package becomes

immediately corrected, just by shifting it (possible lo-

gistics operations between a delayed work package

and the next one are shifted as well).

Contrarily to the procedure in the prognostic chart,

further propagation of the impact of this failure to fur-

ICEIS 2010 - 12th International Conference on Enterprise Information Systems

358

ther participants is omitted in this ﬁrst step but each

affected participant directly succeeding the delayed

work package receives a message with a request to

check the own planned end time based on the new

replanned start time

. This procedure may result in

an analog failure propagation, repeating the proce-

dure until the GANTT chart is up-to-date. Information

about delays can also be used to precisely calculate

company speciﬁc reliability indices to characterize a

company objectively, integrally motivating the partic-

ipants to actually update their scheduling contempo-

rary. To realize this in a valid way, it is necessary to

count and measure actual faults by this company. This

is possible by inventing failure tags, classifying fail-

ures in a scheme which is readable for the software

system as, e.g., machine breakdown, delay(s) of pre-

decessor(s) in the cooperation, or delay(s) at suppliers

or subcontractor(s) for the own work packages.

This scheme can be augmented easily, which is

not of importance here. Besides a fair calculation of

reliability indices of the participants, this paves also

the way for a few other functionalities. If somebody

states delay(s) of predecessor(s) as reason for the de-

lay, this is only plausible if there is a delay of prede-

cessors, which can be checked automatically by using

the same feature for the predecessors. Furthermore, if

the predecessor(s) retract their delays (which may be

possible), the participant can be inquired if the orig-

inal schedule can be recovered. This is the currently

implemented way to handle distributed replanning.

6 CONCLUSIONS & PROSPECTS

The paper introduced different approaches to cooper-

ation generation, discussing their strengths and weak-

nesses. Further, we introduced an intelligent support

system to manage enterprise cooperations which has

been implemented as web-application. Finally, re-

planning strategies have been discussed. Note, that

we had to leave out many details in our description of

the system and the algorithms here.

Currently, the methods are evaluated under practi-

cal conditions in a beta-test phase with selected com-

panies. From a research point of view we proclaim

substantial progress towards a practically applicable

solution of the problem of cooperation generation but

as described above, there are still issues and disad-

vantages no matter which of the presented approach-

es one chooses for realization. This means there re-

mains still a lot of work for the future: There are

The start time itself cannot be inﬂuenced by him, be-

cause if preceding participants are delayed, this can be seen

as a ﬁxed constraint.

e.g. open problems dealing with work package split-

ting or a subsequent negotiation of bid prices.

Further possible extensions of the introduced

strategies are, e.g., the integration of procurement for

purchased parts, better support of rush orders, and ad-

dressing functionalities for a ERP/PPS integration.

ACKNOWLEDGEMENTS

The authors thank the German Academic Exchange

Service for funding their research.

REFERENCES

Coello, C. A. C. and Lamont, G. B. (2004). Applications

of Multi-Objective Evolutionary Algorithms. World

Scientiﬁc Publishing Company, Singapore. ISBN: 9-

812-56106-4.

Corman, T., Leiserson, C., and Rivest, R. (2001). Introduc-

tion to Algorithms. MIT Press, Cambridge London,

edition. ISBN: 0-262-03141-8.

Lässig, J. (2007). On a Resource and Time Assignment

Problem in an Online Auction Scenario. In Proceed-

ings of the 3

Indian International Conference on Ar-

tiﬁcial Intelligence, pages 743–762, Pune, India.

Lässig, J. (2009). Algorithms and Models for the Genera-

tion and Control of Competence Networks. Disserta-

tion, Chemnitz University of Technology.

Lässig, J., Heinrich, S., and Dürr, H. (2007). Generation

of SME Production and Logistics Networks with Ex-

tremal Optimization and Fitness Threshold Accepting.

In Proceedings of the International Conference on

Artiﬁcial Intelligence and Pattern Recognition, pages

313–319, Orlando, USA.

Martinez, M. T., Fouletier, P., Park, K. H., and Favrel, J.

(2001). Virtual Enterprise - Organisation, Evolution

and Control. International Journal of Production Eco-

nomics, 74:225–238.

Miles, R. E. and Snow, C. C. (1984). Fit, Failure and the

Hall of Fame. California Management Review, 3:10–

28.

Pratta, M. J., Andersonb, B. D., and Rangerc, T. (2005).

Towards the standardized exchange of parameterized

feature-based CAD models. Computer-Aided Design,

37(12):1251–1265.

Sandholm, T. (2002). Algorithm for Optimal Winner Deter-

mination in Combinatorial Auctions. Artiﬁcial Intelli-

gence, 135:1–54.

Shaw, M. J. and Fulkerson, W. F. (2001). Introduction to

the Technology Strategy and Industrial Applications of

Information-Based Manufacturing. Springer, Berlin

Heidelberg New York. ISSN: 0920-6299.

Teich, T. (2002). Extended Value Chain Management -

ein Konzept zur Koordination von Wertschöpfungsnet-

zen. Habilitation, Chemnitz University of Technology,

Germany.

NEW APPROACHES TO ENTERPRISE COOPERATION GENERATION AND MANAGEMENT

359