THROTTLING DDoS ATTACKS USING DISCRETE LOGARITHM
PROBLEM
Avinash Darapureddi, Radhesh Mohandas and Alwyn R. Pais
Information Security Lab, Department of Computer Engineering, NITK, Surathkal, Karnataka, India
Keywords:
Distributed denial of service, Application of discrete logarithm problem, Source throttling, CPU stamps, Ap-
plication level attacks.
Abstract:
Amongst all the security issues that the internet world is facing, Distributed Denial of Service attack (DDoS)
receives special mention. In a typical DDoS attack, an attacker runs a malicious code on compromised systems
to generate enormous number of requests to a single web server. The flood of incoming requests makes the
victim web server resources to wear out completely within a short period of time; thereby causing denial of
service to the legitimate users. In this paper we propose a solution to trim down the impact of DDoS attacks by
throttling the client’s CPU i.e., to make clients pay a stamp fee which is collected in terms of resource usage
such as CPU cycles. Our proposed solution makes use of the discrete logarithm problem to generate the CPU
stamps.
1 INTRODUCTION
Distributed Denial of Service(DDoS) attacks have
been increasing in recent times. Application level
DDoS attacks are the worst of such attacks and even
companies such as Microsoft, Yahoo are not immune
to them. In the present day web applications the client
sends a request for a resource to a web server with just
one click, but the latter has to process lots of data to
respond to that request which is an order of higher
magnitude. This computation difference favours the
attacker to tie up the web server by flooding requests
with group of compromised systems.
In this paper we propose a solution to trim down
the impact of DDoS attacks by throttling the client’s
CPU i.e., to make client pay a stamp fee which is col-
lected in terms of resource usage such as CPU cy-
cles. Our proposed solution makes use of the Dis-
crete Logarithm Problem (DLP) (Darrel. Hankerson
and Vanstone, 2004) to generate the CPU stamps and
re-compute the same on change of request, everytime.
We propose to use DLP, as it is mathematically com-
plex to solve this on current day non-quantum com-
puters in polynomial time.
Rest of the paper is organized as follows. Section
2 presents related work. Working of the proposed so-
lution is shown in Section 3. Section 4 will discuss
about algorithms. Implementation results and com-
parison with integer factorization are shown in Sec-
tion 5 and we conclude the paper in Section 6.
2 RELATED WORK
(Saraiah and et al, 2009) have proposed a solution to
reduce the impact of a DDoS attacks on a web server
by throttling the clients CPU using integer factoriza-
tion to generate CPU stamps. The protocol flow of
the proposed solution is as follows. A client sends a
request to web server for a webpage. The server starts
a session and retrieves primes from pre-computed
primes based on the server time and the client IP
address and sends the product integer along with a
JavaScript. The client will commit its resources and
factors the integer into its prime factors and sends to
the server. The server will verify whether the prod-
uct of prime factors sent by the client are equal to the
original integer sent by the server and decides to pro-
cesses or drop the request.
(Tuomas Aura and Leiwo, 2000) had showed how
stateless authentication protocols and the client puz-
zles can be used to prevent DoS attacks that exhaust
the server resources.The summary of the solution is
as follows. Initially, server asks the client to solve
a puzzle by committing its resources. Based on the
commitment of the client in solving the puzzle, the
server allocates the resources to the client.
(Wang and Reiter, 2003) proposed a puzzle mech-
anism called puzzle auction. In this, the auction lets
each client determine the difficulty of the puzzle it
solves and allocates server resources first to the client
that solves the difficult puzzle when the server is busy.
263
Darapureddi A., Mohandas R. and R. Pais A. (2010).
THROTTLING DDoS ATTACKS USING DISCRETE LOGARITHM PROBLEM.
In Proceedings of the International Conference on Security and Cryptography, pages 263-269
DOI: 10.5220/0002981502630269
Copyright
c
 SciTePress

(Back, 2002) proposed a solution using Hashcash
in May 1997. It was originally proposed as a mecha-
nism to throttle systematic abuse of un-metered inter-
net resources such as email, and anonymous remail-
ers. In his paper Hashcash was used as a CPU cost-
function to compute a token which can be used as a
proof-of-work.
(Dwork and Naor, 1992) presented a computa-
tional technique for combating junk mail, in partic-
ular and controlling access to a shared resource. The
main idea is that a user is required to compute a mod-
erately hard, but not intractable, function in order to
gain access to the resource, thus preventing frivolous
use.
All these mechanisms make the attacker to pay the
CPU stamp fee. However there are some drawbacks
in the proposed solution in (Saraiah and et al, 2009).
We come up with a solution to overcome this draw-
back with less overhead on the server and with more
throttling effect.
3 PROPOSED SOLUTION
3.1 Definitions
In our solution we use the DLP, on which many cryp-
tosystems are built. Before going into details, we
present definitions to be used in our solution.
Let p be an odd prime, Z
p
= {0, 1,..., p − 1} a
finite field, Z
∗
p
the set of integers which are rela-
tively prime to p i.e., Z
∗
p
= {a ε Z
p
|gcd(a, p)
.
= 1}
⇒ Z
∗
p
= {1,..., p −1}. Let α be a generator of Z
∗
p
i.e.,
Z
∗
p
= { α
0
mod p , α
1
mod p ,..., α
p−1
mod p } and β be
a non zero integer in Z
p
such that
β ≡ α
x
mod p (1)
The problem of finding x in equation(1) is called Dis-
crete Logarithm Problem. It can be denoted as
x = log
α
β (2)
For example let p = 11,Z
∗
p
=
{1,2,3,4, 5,6, 7,8, 9,10}, α = 2 a generator. Given
β = 9 in equation(1); 9 ≡ 2
x
mod11. By exhaustive
search in Table 1 the value of x is 6. When p is small
it is easy to find x, but when p is large then table will
be large and then it is hard to find x. It is easy to find
out β when α,x, p are given but it is hard to find out x
when α,β, p are given.
Table 1: Exhaustive search into exponent table.
x 0 1 2 3 4 5 6 7 8 9 10
α
x
mod p 1 2 4 8 5 10 9 7 3 6 1
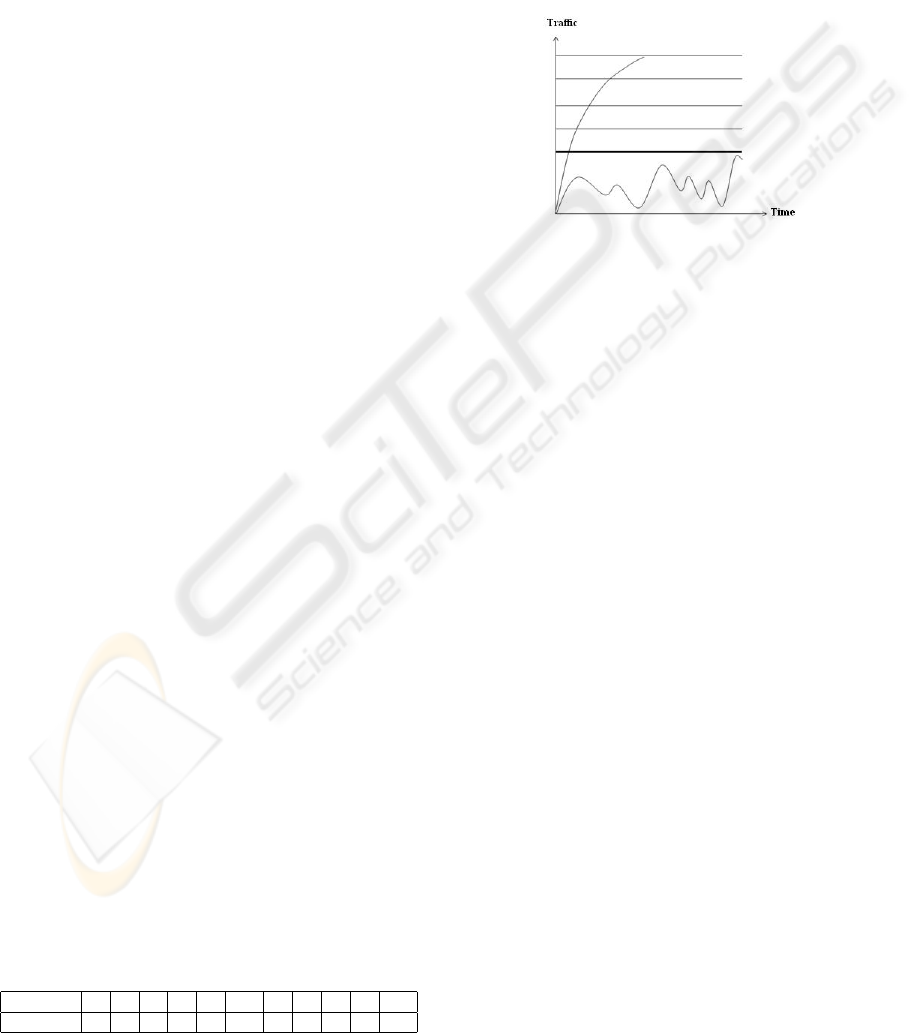
3.1.1 Threshold Value
In Figure 1 dark horizontal line indicates the Thresh-
old value, at which the server can handle maximum
number of requests without straining its resources.
And the curve below the Threshold value indicates
normal flow of traffic and other curve denotes the ab-
normal flow of traffic. Our solution is invoked when
number of requests arriving at the server are more
than the Threshold value.
Figure 1: Threshold Value.
3.2 Proposed Solution
Notations. We make use of the following notations
throughout this paper.
p: An odd prime.
Z
p
: A finite field.
Z
∗
p
: The set of integers which are relatively prime to
p i.e., Z
∗
p
= {1,..., p − 1}.
α: A generator of Z
∗
p
.
β: An integer in finite field other than zero and one
i.e., {β ε Z
p
|β 6= 0or1}
pdigits: Number of digits in prime p
x: value computed using equation(2).
The flow of operations is as follows
1. Client sends a request to the web server for a re-
source.
2. Server starts a session and sends (p, α,β) values
along with the JavaScript.
3. Client computes x and sends (p, α,β, x) values to
the server.
4. The server verifies whether (p,α, β) values sent
by the client are same as the values sent by the
server to the client in step 2 and then verifies
whether β ≡ α
x
mod p. If not equivalent server
drops the request otherwise processes it.
SECRYPT 2010 - International Conference on Security and Cryptography
264

3.2.1 Description of Solution
Based on the server load the server varies pdigits
value from 2 to 8. In our solution, we pre-computed
primes such that (p − 1)/2 is also a prime this is to
overcome Pohlig-Hellman attack(Darrel. Hankerson
and Vanstone, 2004). One generator for each field
is pre-computed and stored. The values (p,α) are
retrieved from pre-computed primes and generators
based on the server load and server time since last
bootup. β is a random value between 2 to (p −1). The
server sends (p,α,β) values to the client and makes
client to compute x.
An attacker with a malicious client will not send
x values to the server . Hence, all such requests are
dropped by the server. Alternately a progressive at-
tacker can modify his malicious client to read the
JavaScript and to compute x values. In that case the
client has to pay resources and consequently the at-
tack rate drops down drastically. Moreover, if the at-
tack deepens, the server increases pdigits which re-
sults in throttling of malicious clients.
3.2.2 Efficient Pre-computation of Generators
The standard algorithm to generate α is to pick a ran-
dom g from Z
∗
p
and find if it is a generator. The algo-
rithm is as follows
1. Picks a random number g between 1 and p to
be a potential generator.
2. Checks to see if g
(p−1)/2
mod(p) = 1. If yes go
back to step 1.
3. Compute g
2
mod p, g
3
mod p,.until either
(a) The answer is 1 (go back to step 1)
(b) The power is (p-1)/2 (we’ve found a gener-
ator)
4. Return the generator found in step 3.
This approach will lead to a pre-computation time
of around 36 hours for the whole space of primes
smaller than 8-digits.
We improvised this by making use of boolean ar-
ray and not computing directly the step 2 of above
algorithm as it is a costly operation (consumes more
CPU cycles).
1. Take a boolean array isNotGenerator[] of size p
and initialize to false and isNotGenerator[0] =
true
2. Picks a random number g between 1 and p to
be a potential generator.
3. If isNotGenerator [g] = true then g ← (g +
1)mod p.
4. answer← g, count←2
5. Compute isNotGenerator[answer] = true;
answer = (answer ∗ g)mod p; and increment
count by 1 until either
(a) The answer is 1 (go back to step 3)
(b) The count
.
= (p-1)/2 (we’ve found a genera-
tor)
6. Return the generator found in step 5.
And were able to finish this computation in just 10
hours.
4 ALGORITHM
Before we discuss the algorithm, different scenarios
in which the attacker actively fine tunes his malicious
client to launch distributed attack on the web server
and the countermeasures to overcome these attacks
are presented.
Scenario 1. In this scenario when the attacker ob-
serves that server is sending same (p,α,β) values
for all the requests. He computes x once and ap-
pends this value to every request to perform a
replay attack. Suppose, if the attacker observes
that server is sending same p,α and different β
for all the requests. He computes the exponent
table (which is used for exhaustive search like Ta-
ble 1) once and then searches to find x and as a
result avoids expensive computation. To counter
these two kinds of attack we will generate p dy-
namically based on the server time( difference of
server current time and the server last boot up time
in milliseconds) and this difference is sufficiently
random as varies for every millisecond. So the
prime value generated will be unique for each re-
quest.
Scenario 2. The Table 2 shows the total number of
primes(NP) in each digit whose (p-1)/2 is also
a prime from 2 to 8. Suppose, if all these pre-
computed primes are saved in an array in a se-
quential manner then the attacker might try to
guess the value of p from its previous values.
This prediction can be done if he maintains pre-
computed primes and uses the same algorithm that
we use to generate p, as the servertime varies by
1 for every millisecond, so he can retrieve nearest
primes from the pre-computed primes and guess-
ing attack can be done. To overcome this predic-
tion and to optimize the storage space, a random
combination of primes and its corresponding gen-
erators are selected. The number of primes so se-
lected is given in Table 2. The primes are selected
THROTTLING DDoS ATTACKS USING DISCRETE LOGARITHM PROBLEM
265

in a random manner and the value of nP of each
digit is unknown, so the prediction of next prime
is impossible to an attacker.We change this com-
bination every half an hour to prevent the attacker
from tabulating the combination for further use.
Table 2: Total Number of primes, primes whose (p-1)/2 also
a prime and selected primes in each digit.
Digits 2 3 4 5 6 7 8
Total no of
primes(TNP) 21 143 1061 8363 68906 586081 5096876
No of primes
whose (p-1)/2 5 18 90 555 3654 26333 198911
also a prime(NP)
No of primes
selected in 5 10 70 300 2000 9000 10000
random(nP)
The Generation algorithm takes in four argu-
ments. servertime, pdigits, selectedPrimes array
(which contains a randomly chosen combination
from the total set of primes), selectedGenerators
array (which contains corresponding generators of
primes selected) and nP which denotes number of
primes for each digit in the selectedPrimes array.
The algorithm used for generation of p dynamically
overcomes the attacks discussed in scenario1 and
scenario2.
Algorithm Generate (p,α,β)
1. mapvalue ← servertime mod nP
2. p=selectedPrimes[pdigits][mapvalue]
3. α = selectedGenerators[pdigits][mapvalue]
4. β= RandomNumber(2,p-1)
Scenario 3. In this scenario the attacker satisfies the
equation (1) but the (p,α,β) values sent by the at-
tacker are not the same as the values sent by the
server. The attacker changes the original values
which is a repudiation attack. To overcome this
attack the server makes use of session variables to
store (p,α,β) values on the server side for verifi-
cation. This is the only storage cost at the server
end and reasonable for the present day memory
on the server. These numbers take 12 bytes and
current server can handle 3K requests per second.
For a 60 seconds timeout the state table goes up to
2.1MB which is tolerable.
Scenario 4. In this scenario the attacker sends gen-
uine (p,α,β) values and instead of finding x he
will send random value between 2 to p-1 i.e., he
will send (p,α,β,random value). To counter this
attack the server will verify whether values sent
by the client are satisfying equation(1) or not.
The probability of such request going through is
1/(p − 2) which becomes small when p is greater
than 100. The probability of that the chosen ran-
dom value is x for 3-digit primes is 0.00272 and
for 4-digit number 0.00023 and this probability
becomes small when p increases.
Scenario 5. For each field one generator is pre-
computed and stored on server side when same
prime encounters the generator sent will be same
only β changes in this case. At this scenario the at-
tacker computes the exponent table once and uses
it when the same prime encounters. In this case
the attacker have to save all the values of α
x
mod p
where x varies from 1 to (p − 1). From Table 2
number of 8 digit primes(NP) are 198911 which
requires a storage space of around 2MB and to
save all the values of beta the storage space re-
quired is 2MB for each 8-digit prime. So the total
storage space required is around 389GB. As this
much storage space is not available in all the com-
promised systems involved in attack, this type of
attack is not practical with the current hardware
technology.
Algorithm used for verification takes in four ar-
guments p,β,α and x values sent by the client.
The verification algorithm overcomes the attacks
discussed in Scenario 3 and Scenario 4.
Algorithm Verification
1. check whether p,α,β are genuine using session
variables saved on the server side.
2. If p,α,β are genuine then do the following
(a) If β ≡ α
x
mod p
i. Process Request
(b) Else Drop Request
3. Else Drop Request
5 IMPLEMENTATION
To test our proposed solution we have used the fol-
lowing setup
Server Configuration. Intel Xeon Quad CPU, pro-
cessor speed 3.60 GHz each, 4 GB RAM, Win
2003 server.
Client Configuration. Intel core2 Duo CPU with
processor speed 3.00 GHz and 2.99 GHz, 2 GB
RAM, Windows XP professional operating sys-
tem.
5.1 Results
To show the effectiveness of our solution we have
used the same web applications as in (Saraiah and
SECRYPT 2010 - International Conference on Security and Cryptography
266

et al, 2009) and modified them to include our solution
i.e., we have used websites with solution and with-
out solution. We have modified the HTML page of
website with solution such that the page consists of
JavaScript which makes the client browser to find x
when p,α,β are given. When a request comes to the
server then server retrieves the number of requests
per second from Windows performance counters and
when it crosses Threshold value the server starts send-
ing p,α,β values to all the clients using cookies in each
response. The client responds with p,α,β,x values,
in which x is found using the JavaScript in the static
page. The server makes use of verification algorithm
and if the conditions are satisfied by the client, the
server will respond with actual page and p,α,β values
in the session variables are modified with new values.
We have measured the time taken by different web
browsers(in milliseconds) to find out x value when
p,α,β values are given and tabulated those readings
in Table 3 . CCB in the Table 3 represents the custom
command line browser built using C#.NET, which an
attacker may build.
Table 3: Time taken(in milliseconds) by different browsers
to find x.
pdigits IE Mozilla Opera Chrome CCB
2 0.92 0.57 0.31 0.78 0.03
3 1.84 1.25 1.13 0.94 0.014
4 10.2 3.89 3.72 2.75 0.214
5 82.37 74.35 45.23 39.64 1.128
6 1013.9 672.89 682.82 543.28 14.428
7 7084.62 5407.38 5907.93 5108.6 145.0675
8 30894.57 26175.07 28907.87 24106.81 1559.611
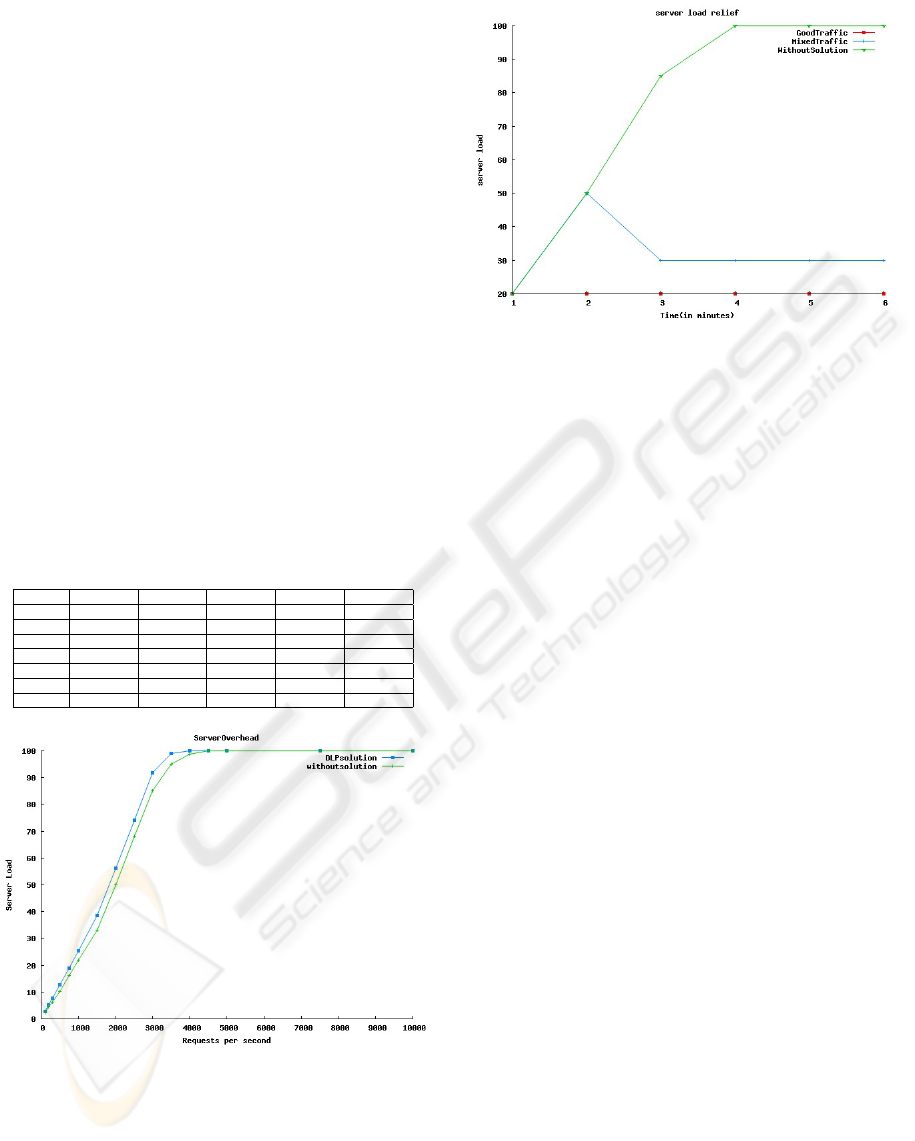
Figure 2: Server Overhead with and without solution.
Figure 2 shows the overhead on the server when
the solution is used and when the solution is not used.
We can observe from the Figure 2 overhead is very
less when our solution is used.
Figure 3 shows the server load relief. We sent a
good traffic(which computes x) of 1000 requests per
second using client1 and bad traffic(which will not
Figure 3: Server Load Relief.
compute x) i.e., attack traffic of about 2000 requests
per second through client2. As a result server load
crosses Threshold value and our solution is invoked
and server starts sending the p,β value to the clients.
The server drops the bad traffic. We can observe in
the Figure 3 the sever load falls down once solution is
invoked.
5.2 Comparison with Integer
Factorization
In this section first we present some drawbacks of so-
lution proposed in (Saraiah and et al, 2009) and then
we show how our solution is more efficient than the
proposed solution in (Saraiah and et al, 2009).
5.2.1 Drawbacks of Solution using Integer
Factorization
As discussed in the (Saraiah and et al, 2009) the gen-
eration of p and q are based on server time since last
boot up and client IP address respectively. In this case
when the requests are coming from single client. p
varies upon each subsequent request but q will not
vary as there is no change in the IP address. To make
q vary upon every subsequent request selected primes
array must be refreshed for every millisecond which
is not possible. And this selected primes array is re-
freshed at periodic intervals say 15 minutes. During
this period of time, the attacker can find p by p = N/q
and avoid the integer factorization computation.
5.2.2 Comparison on the Client Side
From Table 4 and Table 3 we can observe that client
latency in case of DLP solution is significantly more
than Integer Factorization(IF) for the same number of
digits. This is a direct result of the fact that DLP is a
harder problem than IF in terms of computation.
THROTTLING DDoS ATTACKS USING DISCRETE LOGARITHM PROBLEM
267

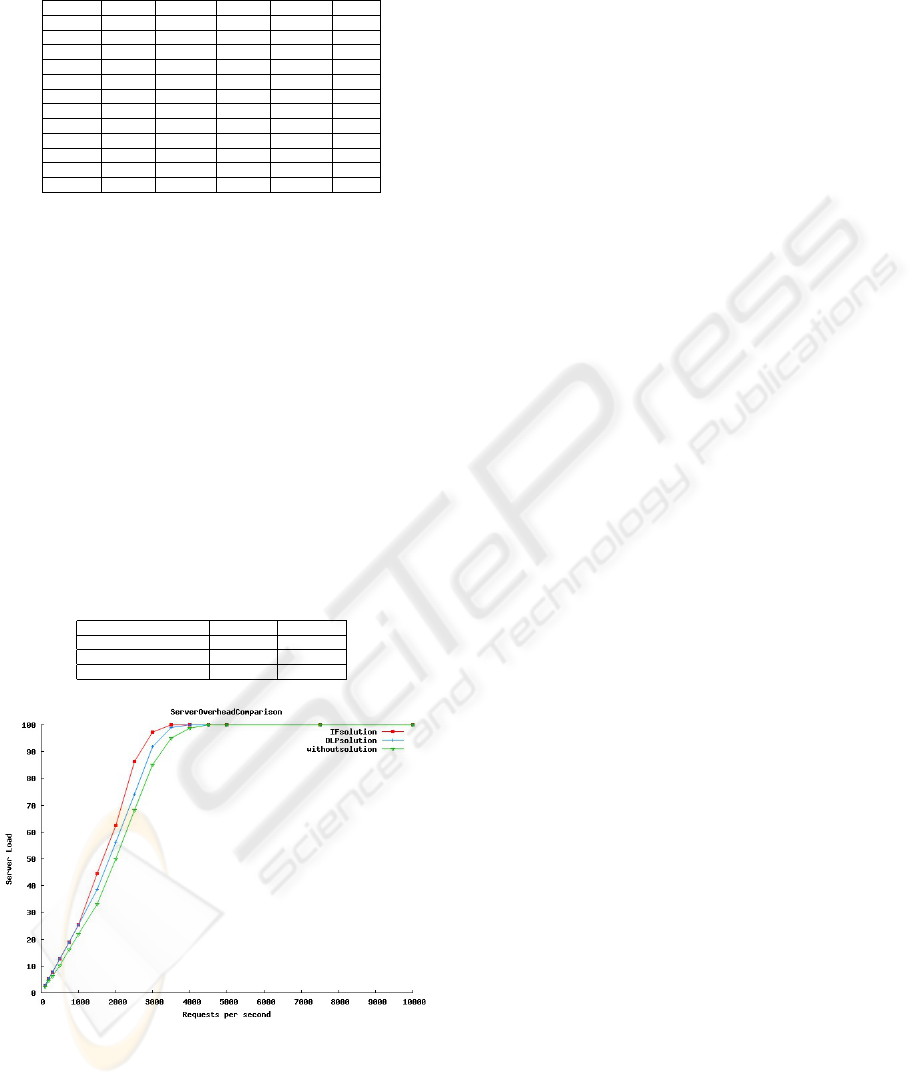
Table 4: Latency in milliseconds of browsers to calculate
factors.
Ndigits IE Mozilla Opera Chrome CCB
5 0 0.2 0 0.2 0
6 0 0.2 0 0.2 0
7 0 0.2 0 0.4 0
8 0 1.8 0 2.2 0.01
9 6 1.8 3 2.2 0.05
10 34 16 22 18 0.05
11 44 23 28 25 0.07
12 265 134 147 147 0.43
13 318 163 169 173 5.60
14 2512 1269 1347 1398 6.62
15 4975 2475 2659 2866 44.6
16 49820 25069 19859 28173 67.5
5.2.3 Comparison on the Server Side
The overhead on the server is less in our solution
than IF. In our solution the parameter for selection
of prime is server time since last bootup, where as
in solution using IF is server time since bootup and
client IP address. As there is no overhead of reading
client IP address (which takes around 1.896163 mil-
liseconds ) in our solution, the overhead on server is
low. The following Table 5 shows the time taken(in
milliseconds) by the server for generation and verifi-
cation algorithms in solutions using IF and DLP. This
is average across 1000 requests per second for varying
server load.
Table 5: Time taken (in milliseconds) for generation and
verification algorithms.
IF DLP
Generation Algorithm 1.945352 0.037941
Verification Algorithm 0.000634 0.077118
Overall Time taken 1.945986 0.115059
Figure 4: Server Overhead Comparison.
Figure 4 shows the overhead on the server due to
solutions using IF and DLP. From the Figure 4 we
can observe that overhead on the server is less in our
solution than the proposed solution in (Saraiah and
et al, 2009).
5.3 Limitations
In this section we present some limitations of our pro-
posed solution.
• When JavaScript is not enabled in the browser
then our solution will not work but now-a-days
most of the web sites require JavaScript to be en-
abled.
• Our solution does not block a particular IP ad-
dress from which an attacker is sending bad traf-
fic(attack traffic). But this problem can be solved
easily by using a inexpensive hardware device.
• Our solution will not work if pdigits value is more
than 8 because the browsers only support up to 16
digit numbers(In JavaScript the function used for
finding x needs multiplication, if pdigits value is 8
then max value will be a 16 digit number). But as
we see from the Table 3 this is sufficient to impose
the maximum tolerable latency on a human user.
• Latency is not fine tunable as we saw in Table 3
that the difference of latency from 6-digit prime
to 7-digit prime is more.
6 CONCLUSIONS
In this paper we proposed a solution which will throt-
tle clients and contains DDoS attack at the applica-
tion level. We have come up with a algorithm to find
a generator faster than the standard random pick and
try algorithm. And came up with a strategy to dif-
ferentiate between good traffic and bad traffic and to
drop the latter during DDoS attacks. Our proposed
solution is more efficient, having 94% less overhead
on the server than the proposed solution in (Saraiah
and et al, 2009). Though we have developed this so-
lution for a web server, the same can be effectively be
applied to any server by making the client pay a stamp
before using up the server resources.
REFERENCES
Back, A. (2002). Hashcash - a denial of service counter-
measure.
Darrel. Hankerson, A. M. and Vanstone, S. (2004). Guide
to Elliptic Curve Cryptography. Springer, NewYork.
Dwork, C. and Naor, M. (1992). Pricing via processing or
combatting junk mail. In In Advances in Cryptology
- Proc. CRYPTO 98. Springer-Verlag: volume 740 of
LNCS, pages 139147, Santa Barbara, CA USA.
Saraiah and et al (2009). Throttling ddos attacks. In Pro-
ceedings of SECRYPT 2009 International Conference
on Security and Cryptography.
SECRYPT 2010 - International Conference on Security and Cryptography
268

Tuomas Aura, P. N. and Leiwo, J. (2000). Dos-resistant
authentication with client puzzles. In Revised Papers
from the 8th International Workshop on Security Pro-
tocols. Vol. 2133, Pages: 170 - 177.
Wang, X. and Reiter, M. K. (2003). Defending against
denial-of-service attacks with puzzle auctions. In Pro-
ceedings of the 2003 IEEE Symposium on Security
and Privacy. Page: 78.
THROTTLING DDoS ATTACKS USING DISCRETE LOGARITHM PROBLEM
269