MULTIMETRIC NETWORK TOMOGRAPHY

Muhammad H. Raza, Bill Robertson, William J. Phillips

Department of Engineering Mathematics and Internetworking, Dalhousie University, Nova Scotia, Halifax, Canada

Jacek Ilow

Department of Electrical Engineering, Dalhousie University, Nova Scotia, Halifax, Canada

Keywords:

Network tomography, Link delays, Multimetric, NTF, NNMF.

Abstract:

We introduce a novel concept of multiple metric network tomography in this paper. The conventional network

tomography observes a single parameter directly and infers another parameter indirectly from the the directly

measured parameter. We consider observing two parameters (packet loss rate (PLR) and path delays) directly

and use both of these parameters to infer a single parameter indirectly. We applied a variation of NTF1 model

of non negative tensor factorization (NTF) for this purpose and estimated link delay. Simulation results should

show a better correlation between the estimated and measured link delays when duplex of metrics is used as

compared to using only the path level link delays for estimating the link delays on a test bed.

1 INTRODUCTION

Network tomography presents a good means to mea-

sure the statistics of interest that may not be measured

directly. Network tomography measures a parameter

actively or passively (that is not desired for network

management), and the desired parameter is indirectly

measured by applying statistical techniques over an

inverse model. Such parameters are essential for net-

work management.

Vardi (Vardi, 1996) was the ﬁrst one to introduce

the term of network tomography for such kind of indi-

rect inference of interested statistics. The research on

network tomography has always concentrated on esti-

mating a single parameter indirectly from another pa-

rameter that is directly measured. Various categories

of network tomography have been mentioned in the

literature in this context (Castro et al., 2004) (Coates

and Nowak, 2001).

The simplest model of network tomography, that

represents the above two examples is shown by the

following equation,

Y = AX, (1)

linking the measured parameters matrix (Y) with the

matrix of unknown parameters (X) with dependence

on the routing matrix (A) of the network. If Y has I

rows and X has J rows, then the size of the routing

matrix (A) is I×J. The rows of A (A

) correspond to

paths from the sender to the receivers and the columns

) correspond to individual links in those paths. An

element (A

) of the routing matrix is 1 if the link j is

included in the path i and 0 otherwise.

In contrast to the conventional tomography model

as discussed above, we propose the idea of direct mea-

surements of multiple metrics to recover indirectly a

single parameter with expectation of getting a better

estimate as compared to using a single directly mea-

sured parameter to estimate a parameter indirectly.

The new model is represented by the equation below,

where Y

and Y

are directly observed in order to es-

timate X indirectly by solving the following inverse

equation.

= AX (2)

For example, instead of recovering link delays from

merely end to end path delays, we can estimated link

delays from a combination of path delays (Y

) and

PLR (Y

). The idea behind this innovation is that a

better input in terms of two interdependent metrics

should produce better estimation than using only one

parameter such as path level delay. This correlation

of two network parameters has been discussed in the

literature. For example, the authors of (Moon et al.,

1998) report on the correlation between delay and loss

observed by a continuous-media trafﬁc source. This

study is to determine the extent to which one perfor-

mance measure could be used as a predictor of the

H. Raza M., Robertson B., J. Phillips W. and Ilow J. (2010).

MULTIMETRIC NETWORK TOMOGRAPHY.

In Proceedings of the International Conference on Data Communication Networking and Optical Communication Systems, pages 80-84

DOI: 10.5220/0002982000800084

 SciTePress

future behavior of the other (for example, whether ob-

served increasing delay is a good predictor of future

loss) so that an adaptive continuous media application

might take anticipatory action based on observed per-

formance.

For this purpose, we have applied one of the varia-

tions of NTF1 model of nonnegative tensor factoriza-

tion (NTF) (Cichocki et al., 2009).

The rest of the paper is organized as follows. Section

2 reviews the related work. Section 3 discusses NTF.

Section 4 details simulation arrangements. Section 5

presents and discusses results. Section 6 concludes

the paper.

2 RELATED WORK

This section investigates related work in the domains

of multiple metric network tomography concept and

the interdependence of link delays and PLR.

2.1 Multimetric versus Additive Metrics

Up to best of our knowledge, there has never been

an implicit consideration of directly measured multi-

ple metrics for indirect estimate of a network metric.

Though, we found an evidence (Bhamidi et al., 2006)

of considering multiple metrics in the form of addi-

tive metrics. A framework was proposed for analyz-

ing topology using ideas and tools from phylogenetic

inference in evolutionary biology. The phylogenetic

inference problem determines the evolutionary rela-

tionship among a set of species. The framework is

built upon additive metrics. Under an additive met-

ric the path metric (path length) is expressed as the

summation of the link metrics (link lengths) along the

path. The basic idea is to use (estimated) distances

between the terminal nodes (end hosts) to infer the

routing tree topology and link metrics. Based on the

framework some inference algorithms have been pre-

sented as an alternative to network tomography.

They (Bhamidi et al., 2006) consider that G = (V,

E) denotes the topology of the network, which is a

directed graph with node set V (end hosts, internal

switches and routers, etc.) and link set E (communi-

cation links that join the nodes). For any nodes i and

j in the network, if the underlying routing algorithm

returns a sequence of links that connect j to i, they say

j is reachable from i. They call this sequence of links

a path from i to j, denoted by P(i, j).

As per their terminology, d(e) can be viewed as

the length of link e, and d(i, j) can be viewed as the

distance between nodes i and j. Basically, an addi-

tive metric associates each link on the tree with a ﬁ-

nite positive link length, and the distance between two

nodes on the tree is the summation of the link lengths

along the path that connects the two nodes. Suppose

T(s, D) = (V, E) is a routing tree with source node s

and destination nodes D. Let

d(E) = d(e) : eεE (3)

denotes the link lengths of T(s, D) under additive met-

ric d. Remember U = s

D is the set of terminal

nodes on the tree. Let

d(U

) = d(i, j) : i, jεU (4)

denote the distances between the terminal nodes.

The above review makes it clear that consider-

ing additive metric is different from multiple metric

based network tomography. Actually this phyloge-

netic based technique is claimed to be an alternative

of network tomography(Bhamidi et al., 2006). There-

fore, our idea of considering multiple metric stays

as a novel way of improving the conventional mono-

metric network tomography.

2.2 Correlation of Link Delays and PLR

The authors of (Moon et al., 1998) examine the cor-

relation between packet delay and packet loss experi-

enced by a continuousmedia trafﬁc source. Their goal

is to study the extent to which one performance mea-

sure can be used to predict the future behavior of the

other (for example, whether observed increasing de-

lay is a good predictor of future loss) so that an adap-

tive continuous media application might take antici-

patory action based on observed performance. They

provide a quantitative study of the extent to which

such correlation exists. There are two examples in

this regard.

When the buffer reaches its capacity, packet losses

begin to occur. The receiver of the continuous-media

application thus sees increased delay, and eventually

losses.

When packets from a continuous-media applica-

tion arrive at a buffer that is already full, they are

dropped. As other sources (for example, TCP con-

nections) detect congestion and decrease their trans-

mission rate, the queue length at the buffer will de-

crease, and packets from the continuous-media appli-

cation will start to be queued, rather than dropped.

The receiver sees losses followed by high, but possi-

bly decreasing, packet delays.

They introduce a lag, loss-conditioned average de-

lay, in calculating the average delay conditioned on

loss. Speciﬁcally, the average packet delay, condi-

tioned on a loss occurring at a time lag j packets in

the past, is the average delay of all packets in the trace

MULTIMETRIC NETWORK TOMOGRAPHY

that have a loss j packets before them in the trace.

That is,

E[d

| l

i− j

= 1] =

∑

kεP

/ | P |, (5)

where P = k : l

k− j

= 1 and l

= 0.

If the loss-conditioned average delay at a positive

lag of j is higher than the unconditional average delay

(that is, the delay averaged over all received packets),

then the packets that arrive j packets after a loss have

a higher average delay than the unconditional average

delay. That is, a loss occurring j packets in the past

can be taken as a precursor to a higher delay later.

This discussion shows that delay and PLR

are interdependent and correlated based on loss-

conditioned average delay. This evidence motivated

us to consider multimetric network tomography. We

have applied NTF tool to carry out the multiple metric

network tomography and NTF is brieﬂy described in

the next section.

3 NONNEGATIVE TENSOR

FACTORIZATION (NTF)

We researched for a mathematical technique that

could deal with multiple metrics and is capable of

matrix factorization. Matrix factorization is an im-

portant area in signal processing and linear algebra,

with applications in many other areas. Blind source

separation (BSS) and related methods, for exam-

ple, independent component analysis (ICA), employ

a wide range of unsupervised learning algorithms and

have found important applications from engineering

to neuroscience (Cichocki et al., 2009).

Tensors are generalizations of vectors and ma-

trixes, for example, a third-order tensor (or three-way

array) has three modes (or indices or dimensions).

A tensor is a multi-way array or multi-

dimensional matrix. The order of a tensor is the num-

ber of dimensions, also known as ways or modes.

Tensor can be formally deﬁned as following. Let I

, . . . , I

ε N denote index upper bounds. A tensor

Y ε R

,...,I

of order N is an N-way array where el-

ements y

,...,i

are indexed by i

ε 1,2,...,I

for 1≤

n ≤ N.

Unfolding or matricization or ﬂattening is a pro-

cess of reordering the elements of an N-th order ten-

sor into a matrix. Two of the most commonly used

decompositions are the Tucker decomposition and

PARAFAC, which are often considered as higher or-

der generalizations of the matrix singular value de-

composition (SVD) or principal component analysis

(PCA). A model which imposes nonnegativity on fac-

tor matrices is called the NTF (Nonnegative Tensor

Factorization) or Nonnegative PARAFAC (Cichocki

et al., 2009).

Figure 1 illustrates one of the three ways of the

basic 3D NTF1 model, which is an extension of the

NTF model. As per NTF1 model, given a three-

way (third-order) tensor formed by a set of matrices

εR

I×T

(q = 1, 2, .,.,.Q), formulates a set of nonneg-

ative and sparse matrices A εR

I×J

, C εR

Q×J

, and A

εR

I×J

for q = 1,2,.,.,.Q with reduced dimensions

(J << I < T

Global matrix representation using row-wise un-

folding of the three-way array is shown in Figure 1

and is expressed (error free model) as Y

= AD

. In

this case the sub-matrices are deﬁned as X

, D

Thus, only the mixing matrix A and the set of scaled

source matrices X

need to be found whereas due to

scaling ambiguity the matrix C does not need to be

calculated explicitly (Cichocki et al., 2009).

There are several possible approaches to ﬁnd or

identify extended NTF1 model such as global strat-

egy, or local strategy, or a combination of both. A

global strategy based on alternating minimization of

cost function is shown in the following equation.

(YkAX) =

kY − AXk

(6)

A local strategy based on alternating minimization of

cost function is shown in the following equation.

kAX

) =

− AX

(q = 1,2, .,.,.,., .,Q)

(7)

Figure 1: Decomposition into two matrices using row-wise

unfolding (Cichocki et al., 2009).

We plan to employ local strategy based on alter-

nating minimization of cost function in the simula-

tions. For solving the model, Y

= AX, NTF will

be applied to recover link delays (X) from a duplex of

metrics (path delays (Y

) and PLR (Y

)). Two matri-

ces (Y

and Y

) will be input to NTF and a matrix,

X, will be determined as per row wise decomposition

shown in Figure 1. The parameters (Y

, Y

, and X

(for bench marking)) of the multimetric network to-

mography model will be determine from a laboratory

test bed. The setup of the test bed and simulations is

discussed in the next section.

DCNET 2010 - International Conference on Data Communication Networking

4 SIMULATION ARRANGEMENT

FOR MULTIMETRIC

NETWORK TOMOGRAPHY

We collected data from a test with two options.

Firstly, we determined link delay from path delays by

using non negative matrix factorization (NNMF) by

using Cisco Service Level Agreement (CSLA). Sec-

ondly, we determined link level delay from a com-

bination of path delay and PLR by using CSLA and

Real Time Transport Protocol (RTP) (RFC 1889) by

using row wise unfolding of NTF1 model. This sec-

tion discuses the test bed and simulation arrangement,

delay estimation by using path delay input to NNMF,

and link delay estimation from the combined data of

path delay by CSLA and RTP.

We set up a test bed in the Advanced Internet-

working Laboratory (AIL) at Dalhousie University

that consists of six 38 series Cisco routers, Agilent

Router Tester (N2X), and a Multi Router Trafﬁc Gra-

pher (MRTG) capable workstation. OSPF routing has

been implemented on routers and N2X. The test bed

is of smaller size and has limited number of links, be-

cause we have to collect the actual values of the link

delays for bench marking the accuracy of estimated

link delays. We intent to prove that the estimated link

delays are close to the actual link delays. In contrast

to this test bed, the practical networks are larger in

scale, but scalability is not an issue as NNMF and

NTF can handle larger sizes of matrices (Cichocki

et al., 2009).

The Echopath option of the CSLA was imple-

mented to send four probes and collect the cumula-

tive round trip time (RTT) from source to each hop.

All probes were grouped together. All the probes in

the group start at the same time. The group of probes

was repeated 100 times with a time difference of 10

sec between two consecutive repetitions. The MRTG

enabled workstation veriﬁed the end to end RTT. The

selected links were stressed by two sources: extended

ping on selected links and trafﬁc injected from the

N2X.

Figure 2 shows the test bed with the four probes

and two of the links (1 and 6) were stressed with an

extended ping of 200 Bytes. The other source of dis-

turbance was the trafﬁc from the Agilent router tester

(N2X). The module 1 of N2X was generating a vari-

able packet size from 1000 Bytes to 1500 Bytes. The

size of the probes in CSLA was 10 Bytes for this sce-

nario. In this case also, the condition of the network

remains unchanged during the CSLA operation.

Figure 2: Testbed Setup with a mixture of extended pings

and N2X trafﬁc.

4.1 Estimation of Link Delay from Path

Delays

In this ﬁrst part of the simulations, we estimate link

delays from path level delays and then determine the

correlation between the estimated and measured link

delays. The data obtained from the CSLA is in the

form of accumulative hop-wise round trip time, the

following steps are followed to process the data for

obtaining two matrices; a matrix of end to end delays

and a matrix of link level delays:

1. A parsing software, written in java, extracts link

delays and end to end (path) delays in the form of

two matrices. From the accumulative round trip

time from source to each hop, hop to hop delays

are calculated to form the link delay matrix. From

the accumulative round trip time from the source

to the destination, end to end delay matrix is de-

termined.

2. Path level delays (V) are input to NNMF. The

Matlab tool NMFpack (Hoyer, 2004) has been

used for NNMF factorization. The NMFpck Mat-

lab package implements and tests various versions

of NNMF with the feature of sparsity. The spar-

sity for the routing matrix is kept ﬁxed at 0.5 in all

the tests and the sparsity of the link delays varies

from 0.1 to 0.9.

3. The coefﬁcient of correlation between the esti-

mated link delay (H) and actual link delay (X)

is determined by using a modiﬁed component of

EEGLAB. The EEGLAB is an interactive Mat-

lab toolbox for processing continuous and event-

related EEG, MEG and other electrophysiological

data.

For ﬁnding the correlation coefﬁcient, matching

rows in two matrices (H and X) are found and

their correlation is determined. As a result a col-

umn vector of correlation coefﬁcients between the

best-correlating rows of matrices H and X is ob-

tained along with other by-products.

Figure 3 shows a correlation between the esti-

mated and true link delays.

MULTIMETRIC NETWORK TOMOGRAPHY

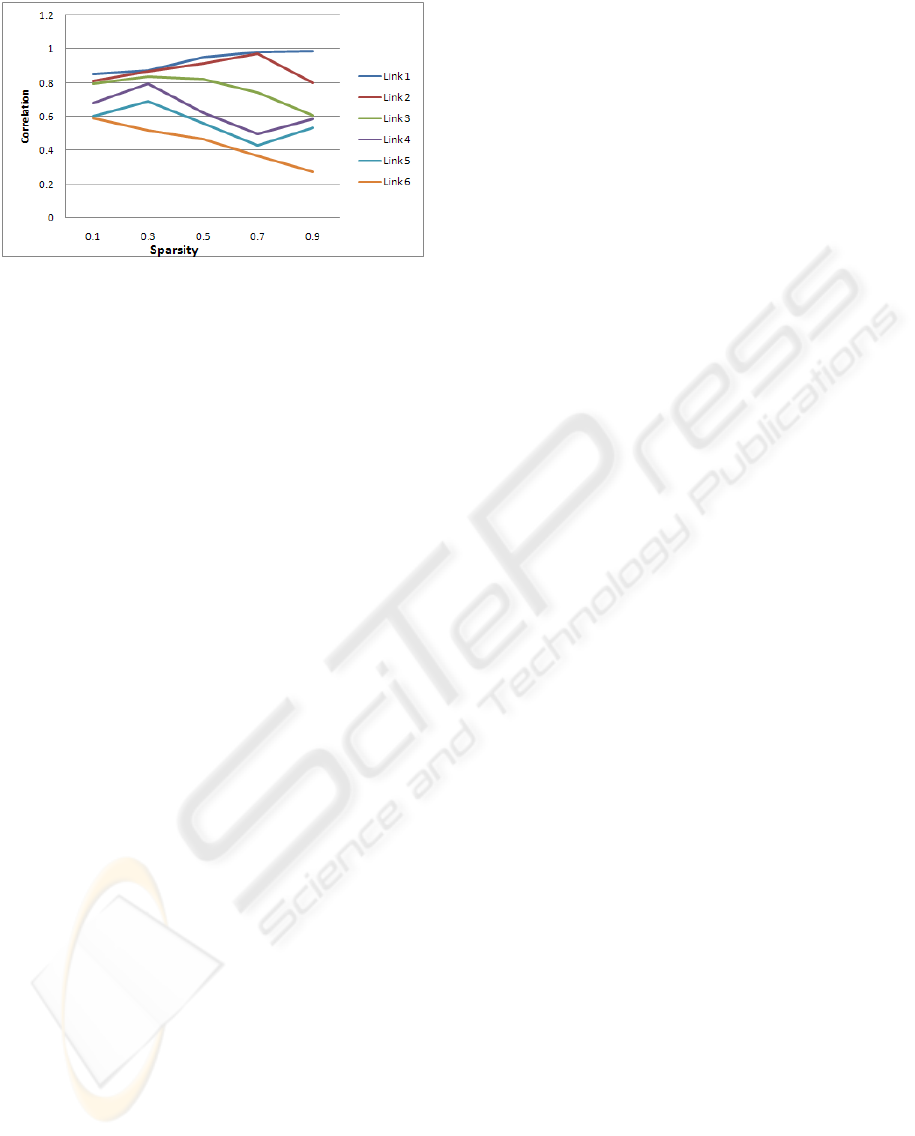
Figure 3: Correlation between H and X with a mixture of

extended pings and N2X trafﬁc.

4.2 Estimation of Link Delay from a

Combination of Path Delays and

RTP Data

In the second part of the simulations, we intend to es-

timate link delays from a combination of path level

delays and PLR data. The correlation between es-

timated and measured link delays will be measured

again and we expect this correlation to be better than

the correlation shown in Figure 3. In the same test

bed, we will inject two types of trafﬁc; CSLA and

RTP. We are in a process of getting a combination of

path level delay and PLR. This data will be used to

recover link level delays by inputting this data to row

wise unfolding of NTF1 model with local strategy

based on alternating minimization of the cost func-

tion.

5 CONCLUSIONS

We introduced a novel concept of multiple metric net-

work tomography in this paper. We estimated link

delays from path delay for the mono-metric network

tomography. The correlation between the estimated

and measured link delays was close to 1 depending on

the sparsity. We are in a process to estimate link de-

lays from two input parameters; path delays and RTP

data. We expect the correlation between the estimated

link delays (by using multimetric) and measured link

delay to be better than using a mono-metric (path de-

lays).

REFERENCES

Bhamidi, S., Rajagopal, R., and Roch, S. (2006). Net-

work delay inference from additive metrics. In Arxiv

preprint math/0604367.

Castro, R., Coates, M., Liang, G., Nowak, R., and Yu, B.

(2004). Network tomography: Recent developments.

In Statistical Science. Volume 9, 499–517.

Cichocki, A., Zdunek, R., Phan, A. H., , and ichi Amari,

S. (2009). Nonnegative Matrix and Tensor Factor-

izations: Applications to Exploratory Multi-way Data

Analysis and Blind Source Separation. Wiley.

Coates, M. and Nowak, R. (2001). Network tomography for

internal delay estimation. In 2001 IEEE International

Conference on Acoustics, Speech, and Signal Process-

ing, Proceedings (ICASSP’01). IEEE.

Hoyer, P. (2004). Non-negative matrix factorization with

sparseness constraints. In The Journal of Machine

Learning Research. MIT Press Cambridge, MA, USA,

Volume 5, 1457-1469.

Moon, S., Kurose, J., Skelly, P., and Towsley, D. (1998).

Correlation of packet delay and loss in the internet. In

Univ. Massachusetts, Amherst, MA, Tech. rep. CMP-

SCI.

Vardi, Y. (1996). Network tomography: Estimating source-

destination trafﬁc intensities from link data. In Jour-

nal of the American Statistical Association. Volume

91, 365–377.

DCNET 2010 - International Conference on Data Communication Networking