PERFORMANCE EVALUATION OF THE TLS HANDSHAKE IN THE
CONTEXT OF EMBEDDED DEVICES
Manuel Koschuch, Matthias Hudler and Michael Kr
¨
uger
Competence Centre for IT-Security, FH Campus Wien, University of Applied Science
Favoritenstrasse 226, 1100 Vienna, Austria
Keywords:
Elliptic curve cryptography, Transport layer security, Embedded devices, Sensor networks, Performance eval-
uation.
Abstract:
With the strong advent of mobile and embedded devices communicating in a wireless way using the air inter-
face, the need for secure connections, efficient en- and decryption and strong authentication becomes more and
more pronounced. The Transport Layer Security (TLS) protocol provides a convenient and well researched
way to establish a secure authenticated connection between 2 communicating parties. By utilizing Elliptic
Curve Cryptography (ECC) instead of the more common RSA algorithms, asymmetric cryptography is feasi-
ble even for tiny integrated devices. However, when dealing with heavily resource constrained appliances, it
does not suffice to speed up just the cryptography related computations, but to also keep the communication
necessary to establish a secure connection to a minimum, in order not to drain the scarce energy resources
of the small devices. In this work we give a thorough investigation of the communication overhead the TLS
handshake requires when used in conjunction with elliptic curve cryptography, together with experimental re-
sults using our own library handcrafted to support ECC on embedded systems. The results give implementers
a useful guide for weighing security versus performance and also justifies the need for new authentication
methods, requiring less communication overhead.
1 INTRODUCTION
While only several years ago we were mainly used
to complete our work using stationary, powerful per-
sonal computers, the switch to the long announced
“ubiquitous computing” has not only been already
made, but almost surpassed all initial speculations;
currently we are surrounded by small, portable, mo-
bile devices, which we either interact with knowingly
(like PDAs, cellphones or smartphones) or unknow-
ingly (like sensor networks). All these devices, as dif-
ferent as they may be in looks or function, share some
common characteristics: they are heavily challenged
in terms of available computational power, memory
and energy. Especially the latter results in some se-
rious complications when trying to use algorithms or
protocols developed for stationary PCs on these mo-
bile devices; yet the need for secure and authenti-
cated communication using these wireless appliances
is obvious. So to enable the same level of security
present on PCs one has to look at two main parts:
the cryptographic calculations performed by the de-
vice have to be implemented in an efficient, memory-
saving way. And the exchange of messages during
the protocol has to be kept to a minimum, since radio
transmissions usually put the biggest load on the con-
strained energy resources. Especially in the context of
Wireless Sensor Networks (WSNs), where a huge (i.e.
several thousands) of nodes has to communicate self-
sustained for a considerable amount of time, every ad-
ditional message sent that does not serve the purpose
of transmitting data can be considered a waste of pre-
cious energy. In this work we look at the asymmetric
parts of the Transport Layer Security (TLS) Protocol
in detail, especially how many messages have to be
exchanged to establish a secure connection, and how
an increase in security influences the number of mes-
sages and the load on the participating parties. Finally
we observe how Elliptic Curve Cryptography (ECC)
can be utilized to allow for higher security with lower
performance requirements than RSA based solutions
can offer. To the best of our knowledge, while the
general performance impact of elliptic curve cryptog-
raphy on the SSL/TLS protocol has been quite thor-
oughly examined (e.g. (Gupta et al., 2002)), the num-
ber of messages and the differences between authen-
35
Koschuch M., Hudler M. and Krüger M. (2010).
PERFORMANCE EVALUATION OF THE TLS HANDSHAKE IN THE CONTEXT OF EMBEDDED DEVICES.
In Proceedings of the International Conference on Data Communication Networking and Optical Communication Systems, pages 35-44
DOI: 10.5220/0002983200350044
Copyright
c
 SciTePress

tication options has not been extensively treated yet.
The remainder of this paper is now structured as fol-
lows:
Section 2 introduces Elliptic Curve Cryptography
(ECC), and its benefits over RSA when using asym-
metric cryptography on constrained devices. Sec-
tion 3 then gives an overview of the Transport Layer
Security (TLS) Protocol, with a focus on the hand-
shake process, which uses asymmetric cryptographic
techniques. Section 4 describes the possible crypto-
graphic primitives employed during a TLS handshake
in detail, where finally Section 5 summarizes the mes-
sages that have to be exchanged by each participating
party and the load put onto them, depending on the
primitives chosen. Finally, Section 6 gives some con-
cluding remarks and defines the course of our future
work.
2 ELLIPTIC CURVE
CRYPTOGRAPHY
An elliptic curve is formed by all the tuples (x,y)
satisfying the simplified Weierstrass equation y
2
=
ax
3
+ bx + c, where a, b ∈ any finite field (Hanker-
son et al., 2004). For the remainder of this work we
focus on prime fields GF(p), containing the integers
up to p − 1, where p is prime. Thus all arithmetic
in GF(p) has to be done modulo p. The points on
an elliptic curve, together with a so-called “point-at-
infinity” serving as the identity element, form an ad-
ditive group, with the operations point addition and
point doubling, depicted in Figures 1 and 2, respec-
tively, for a curve defined over the real numbers. So
a single operation in the elliptic curve group requires
several operations in the underlying field, the exact
number depending on the calculation method used
and the representation of the elements. The basic
building block for secure asymmetric cryptographic
systems utilizing elliptic curve groups is the assumed
intractability of the so-called “Elliptic Curve Discrete
Logarithm Problem (ECDLP)”. Given two points P
and Q on a curve, where Q resulted from adding P
k-times to itself (so Q = k ∗ P, an operation called
“scalar multiplication”), there are no efficient meth-
ods known to determine k. It is generally agreed upon
that the hardness of solving this problem for a 160-bit
underlying finite field is equivalent to solving the in-
teger factorization problem for a 1.024-bit composite
number (Lenstra and Verheul, 2001; Krasner, 2004).
So compared to RSA only a sixth of the bit length
is needed to achieve a comparable level of security.
This property makes elliptic curves especially attrac-
tive in the context of resource constrained devices,
since it means smaller intermediate values to store,
and also smaller signatures and messages to be ex-
changed (Potlapallyy et al., 2002; Ravi et al., 2002).
In related work we focused on the results achiev-
able by an efficient implementation of elliptic curve
primitives for generic fields ((Koschuch et al., 2006;
Koschuch et al., 2008; Lederer et al., 2009)). But
when dealing with mobile devices or sensor motes,
additional focus has to be on the number and size of
messages that have to be exchanged during the execu-
tion of a certain cryptographic primitive.
Figure 1: Point Addition, R = P + Q.
Figure 2: Point Doubling, R = 2P.
3 TRANSPORT LAYER
SECURITY PROTOCOL
The Transport Layer Security (TLS) protocol, as de-
fined in (Dierks and Rescorla, 2006) and extended in
(Blake-Wilson et al., 2006b) and (Blake-Wilson et al.,
2006a), is the current de facto standard for secure,
authenticated connections over insecure mediums. It
is well researched and defined and, through the use
DCNET 2010 - International Conference on Data Communication Networking
36

of different ciphersuites that can be negotiated during
connection setup, also very flexible and versatile. The
protocol basically consists of two parts: an asymmet-
ric one, the handshake part, where authentication of
one (or both) of the communicating parties takes place
and a shared secret is established. The actual con-
nection is then secured using symmetric techniques to
ensure confidentiality and integrity of the exchanged
messages. In our work we focus on the asymmetric
- the handshake - part, since in the setting of mobile
devices, especially sensor motes, usually only small
messages are exchanged and so the time needed to
perform the asymmetric operations by far outweighs
the time needed for the symmetric encryption. The
larger the transmitted messages become, the less im-
portant the time for the asymmetric part (Gupta et al.,
2002).
Figure 3: SSL handshake, optional messages printed italic.
Figure 3 gives an overview of the most general
form of a handshake, where optional messages, that
do not have to be exchanged during every handshake,
are printed in italics. Usually a session is initiated
by the client by sending its ClientHello message, pre-
senting the server a list of supported ciphersuites.
Such a suite contains information about the key ex-
change (ECDH, DH, RSA,...), the signature (DSA,
RSA, ECDSA,...), the hash (SHA-1, MD5,...) and
the symmetric (3DES, AES,...) algorithm to use dur-
ing the connection. The server then answers with
the ServerHello message, containing the ciphersuite
selected for this connection. Transmission of the
server’s certificate in the Certificate message is op-
tional, but usual the case, to allow for at least one-way
authentication. The ServerKeyExchange message is
only sent when the chosen key exchange algorithm
requires information not present in the server’s cer-
tificate (for example when using the ephemeral ver-
sion of the Diffie-Hellman Key Exchange, see Sec-
tion 4 for details). Likewise, the CertifacteRequest
is only used when mutual authentication takes place.
The server finishes its first bunch of messages with the
ServerHelloDone message. The client answers with
its certificate in the Certificate message, if mutual au-
thentication is requested, followed by the information
needed by the server to establish the shared secret via
the ClientKeyExchange message and a signed hash of
all messages exchanged thus far in the CertificateVer-
ify message to prove possession of the private key as-
sociated with the public key in its certificate. Finally,
both parties send the ChangeCipherSpec and Finished
messages, where the latter one is already symmetrical
encrypted with the exchanged key and contains the
hash of all the messages of the entire handshake. The
exact number of messages that have to be exchanged
and the calculations each party has to perform de-
pends on the selected algorithms, as described in the
next Section.
4 ASYMMETRIC PRIMITIVES IN
THE TLS HANDSHAKE
There are two choices of algorithms that influence the
amount of transmission and processing power needed
by the parties during a TLS handshake: the algorithm
used for key exchange and the one used for signing.
The following Subsections give an overview of the
most common ones that we investigated in our work.
4.1 Signature Primitives
There are three main algorithms used to sign the ex-
changed messages:
• The Digital Signature Algorithm/Standard
(DSA/DSS)
• The Elliptic Curve Digital Signature Algorithm
(ECDSA) and
• The Rivest-Shamir-Adleman Algorithm (RSA)
Algorithms 1 and 2 detail the creation and verifi-
cation of a DSA signature, respectively. In practice, p
is usually selected to be of length 1.024 bits, whereas
PERFORMANCE EVALUATION OF THE TLS HANDSHAKE IN THE CONTEXT OF EMBEDDED DEVICES
37

q and x are usually about 160 bit. Signature genera-
tion requires one modular exponentiation with a 160-
bit exponent, a modular inversion of a 160-bit number
and two modular multiplications of 160-bit factors.
Signature verification requires one modular inversion,
three modular multiplications and two modular expo-
nentiations, each with 160-bit operands.
Algorithm 1. DSA Signature Generation.
Input: Domain Parameters D = (p,q, g), private key
x, message m, hash function H
Output: Signature (r,s)
1: Select k ∈ [1,q − 1] at random
2: T ← g
k
mod p
3: r ← T mod q
4: e ← H(m)
5: s ← k
−1
(e + xr) mod q
6: return (r,s)
Algorithm 2. DSA Signature Verification.
Input: Domain Parameters D = (p,q, g), public key
y(= g
x
), message m, signature (r,s), hash func-
tion H
Output: ACCEPT or REFUSE message
1: if r,s /∈ [1,q − 1] then
2: return REFUSE
3: end if
4: e ← H(m)
5: w ← s
−1
mod q
6: u
1
← ew mod q
7: u
2
← rw mod q
8: T ← g
u
1
∗ y
u
2
mod p
9: v ← T mod q
10: if v = r then
11: return ACCEPT
12: else
13: return REFUSE
14: end if
The Elliptic Curve Digital Signature Algorithm
(ECDSA) is the elliptic curve implementation of the
digital signature algorithm. In addition to an elliptic
curve key pair a secure hash function H is needed,
whose output is not longer than n. Algorithm 3 de-
scribes the signature generation process for ECDSA.
Note that the transformation of x to an integer in step
3 can be easily done by just looking at its binary rep-
resentation, regardless whether the involved field is
a prime field or a binary extension field. In addi-
tion, calculations in two different finite fields have
to be performed: the scalar multiplication involves
computation in F
q
, but ¯x in step 4 is calculated mod-
ulo the order n of the base point P. In software im-
plementations this poses not to big a challenge, yet
when implementing this algorithm in hardware some
additional arrangements have to be made. The en-
tire signature generation process requires one scalar
multiplication, one modular inversion and two mod-
ular multiplications, usually in the context of 160-bit
fields.
Algorithm 3. ECDSA Signature Generation.
Input: Domain Parameters D =
(q,FR, S,a, b,P,n,h), private key d, message m,
hash function H
Output: Signature (r,s)
1: Select k ∈ [1,n − 1] at random
2: P
1
← k ∗ P = (x
1
,y
1
)
3: Convert x
1
to an integer ¯x
1
4: r ← ¯x
1
mod n
5: e ← H(m)
6: s ← k
−1
(e + dr) mod n
7: return (r,s)
Algorithm 4 shows the verification of an ECDSA
signature. As in the generation of the signature, cal-
culations with two different moduli are also involved
in the verification process. For signature verification,
one modular inversion, two modular multiplications
and 2 scalar multiplications are required, although the
latter can be interleaved and take in fact only negligi-
ble longer than a single scalar multiplication.
Algorithm 4. ECDSA Signature Verification.
Input: Domain Parameters D =
(q,FR, S,a, b,P,n,h), public key Q, message m,
signature (r,s), hash function H
Output: ACCEPT or REFUSE message
1: if r,s /∈ [1,n − 1] then
2: return REFUSE
3: end if
4: e ← H(m)
5: w ← s
−1
mod n
6: u
1
← ew mod n
7: u
2
← rw mod n
8: X ← u
1
P + u
2
Q = (x
1
,y
1
)
9: if X = O then
10: return REFUSE
11: end if
12: Convert x
1
to an integer ¯x
1
13: v ← ¯x
1
mod n
14: if v = r then
15: return ACCEPT
16: else
17: return REFUSE
18: end if
Finally, Algorithms 5 and 6 show the use of the
RSA algorithm for signing: in fact, signing in this
context just means encrypting a hash with the pri-
DCNET 2010 - International Conference on Data Communication Networking
38

vate key (usually about 1.024 bits in size), requiring
one modular exponentiation with a 1.024-bit expo-
nent. Verification is then done by using the sender’s
public key (usually in the order of magnitude of 16
bits) as the exponent in a modular exponentiation.
Algorithm 5. RSA Signature Generation.
Input: Sender’s private key d, Sender’s public key
(n,e), message m, hash function H
Output: Signature s
1: h ← H(m)
2: s ← h
d
mod n
3: return s
Algorithm 6. RSA Signature Verification.
Input: Sender’s public key (n,e), message m, signa-
ture s, hash function H
Output: ACCEPT or REFUSE message
1: h ← H(m)
2: s
0
← s
e
mod n
3: if s
0
= h then
4: return ACCEPT
5: else
6: return REFUSE
7: end if
4.2 Key Establishment Primitives
As in the case of signature primitives, there are three
main algorithms for establishing a shared key:
• The Diffie-Hellman Algorithm (DH) or its
ephemeral variant (DHE)
• The Elliptic Curve Diffie-Hellman Algorithm
(ECDH) or its ephemeral version (ECDHE) and
• The RSA algorithm
The basic Diffie-Hellman scheme is as follows:
1. Both entities agree on a finite cyclic group G
1
and
a generator g of this group.
2. A chooses a number a, calculates x = g ∗ a ∈ G
and sends x to B.
3. B chooses a number b, calculates y = g ∗ b ∈ G
and sends y to A.
4. A calculates K
0
= y
a
= (g ∗ b) ∗ a = g ∗ b ∗ a.
5. B calculates K
00
= x
b
= (g ∗ a) ∗ b = g ∗ a ∗ b.
1
Note that it does not matter whether this group is writ-
ten additive or multiplicative; in the following description
the ∗ means application of the group operation a, or b re-
spectively, times. So in a multiplicative group we need to
perform an exponentiation, in an additive group a multipli-
cation.
6. Since the law of commutativity holds, K
0
= K
00
.
An attacker knows G,g,x and y, but is assumed to
be unable to calculate a from x (or b from y). The
same approach is taken for the elliptic curve version
of this algorithm, with all exponentiations in the mul-
tiplicative group exchanged by scalar multiplications
in the group of points on the curve. In the non-
ephemeral versions of the protocol, the client usu-
ally receives all the information required to calculate
the shared secret in the server’s Certificate message,
and sends its share of the secret back in the Clien-
tKeyExchange message. Both server and client have
to perform one modular exponentiation (respectively
one scalar multiplication). In the ephemeral case of
the protocol, fresh values are used for each run, so
the server has to generate the (signed) ServerKeyEx-
change message to transmit these values to the client.
The client needs an additional signature verification
step, the server needs to generate one signature, and
perform one modular exponentiation, or a scalar mul-
tiplication in the elliptic curve case. The benefit of
this protocol variant is that it guarantees perfect for-
ward secrecy, meaning that a compromised connec-
tion does not influence the security of past transmis-
sions.
In the case of RSA, the client simply generates
a secret, encrypts it with the server’s public key and
sends it back. The client must thus perform a mod-
ular exponentiation with a very small exponent, the
server has to calculate a modular multiplication with
its (considerably larger) private key. The drawback of
this approach is that the quality of the secret depends
solely on the client.
5 IMPLEMENTATION
AND RESULTS
In our practical implementation we used the Ma-
trixSSL
2
library extended by our own generic cryp-
tographic library supporting elliptic curves over arbi-
trary prime and binary extension fields. Implementa-
tion details of this library are presented in (Koschuch
et al., 2008) and (Koschuch et al., 2006), in this work
we currently only investigated the version without re-
sistance against side-channel attacks. As server we
used an AMD Athlon64 X2 5200+ with one phys-
ical core deactivated, fixed to 2.7GHz. The role of
the client was performed by a 200MHz Compaq iPaq
PDA, running Familiar Linux. The PDA was con-
nected to the server using a USB cable, to avoid the
influence of network devices like router or switches
2
www.matrixssl.com
PERFORMANCE EVALUATION OF THE TLS HANDSHAKE IN THE CONTEXT OF EMBEDDED DEVICES
39

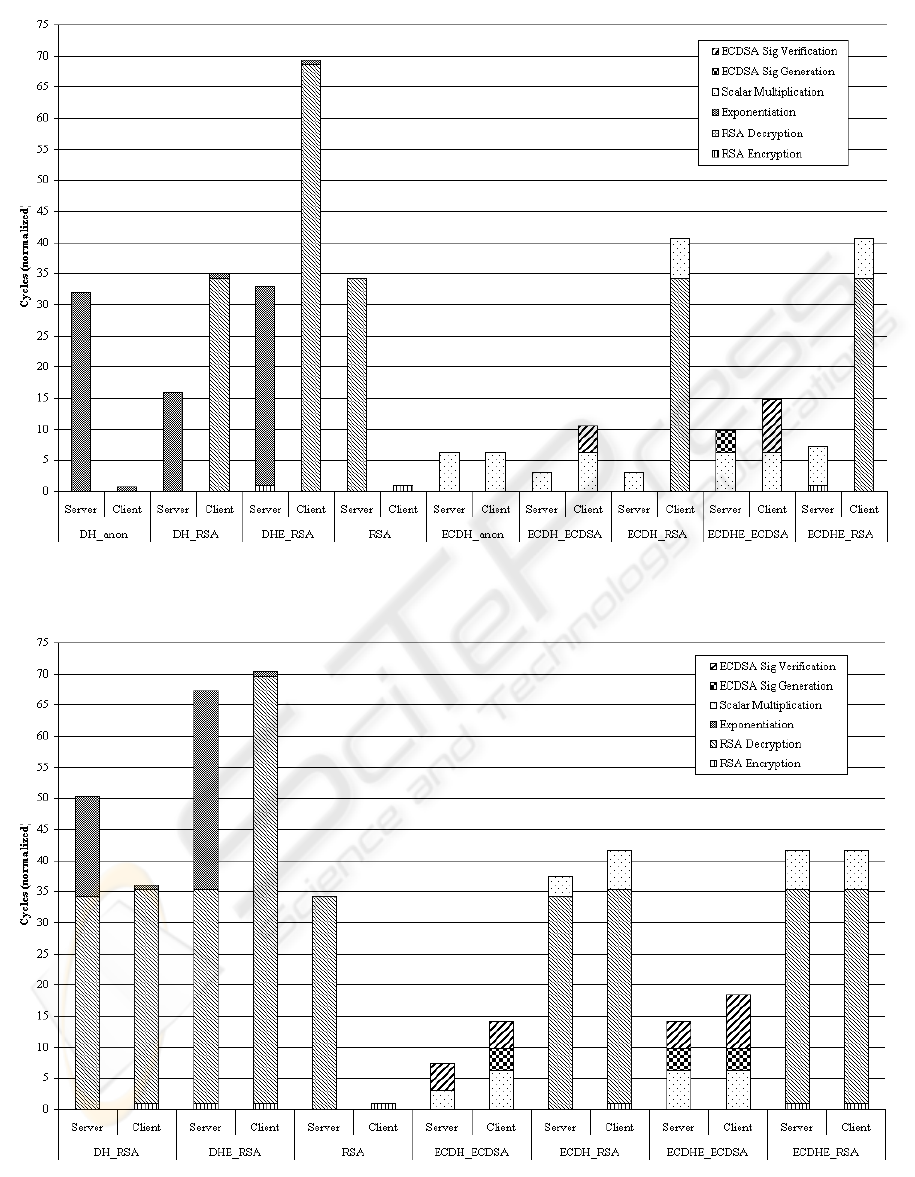
Figure 4: Breakdown of handshake when one-way authentication is used.
Figure 5: Breakdown of handshake when mutual authentication is used.
DCNET 2010 - International Conference on Data Communication Networking
40

on the communication. Tables 1 and 2 give the num-
ber of high-level operations performed by server and
client, respectively, as well as the total number of
messages that have to be exchanged during a full
handshake. It can be observed that the client suffers
always more from increased security than the server,
in terms of messages to be sent as well as in terms
of operations to be performed. Tables 3, 4, 5, and
6 give the cycle count for the individual operations,
normalized so that a modular exponentiation with a
public RSA (that is, 16-bit) key has a cycle count of
one. All elliptic curve operations are performed over
a 192-bit prime field, for RSA 1.024-bit moduli are
used. Here it becomes obvious that increased secu-
rity (like using mutual authentication or ephemeral
Diffie-Hellman) results in a much higher load on the
server when using RSA than when using the elliptic
curve approach, since the server now has to perform
expensive private RSA key operations. For exam-
ple, where the total load on the server almost doubles
when switching from one-way to mutual authentica-
tion in the case of the ephemeral version of Diffie-
Hellman combined with RSA signatures, the elliptic
curve version only increases about 50%. This trend
is also evident when looking at the client, although
here the difference when switching to a higher secu-
rity level is not as pronounced as on the server side.
Finally, Figures 4 and 5 give a detailed breakdown
of the individual operations performed during the
handshake process by server and client, for one-way
and mutual authentication, respectively. An interest-
ing fact is the observation that for most key exchange
methods (with the exception of ECDH ECDSA) the
workload for the client remains the same, regardless
of the type of authentication used. In these cases, the
additional load created by mutual authentication is put
entirely on the serve side. The biggest fraction of the
key exchange process is taken up by the RSA private
key operations, since they are the only one involving
the entire 1.024-bit key. In the elliptic curve variants,
this operation does not exist, resulting in a generally
lower load put on the server. So these figures suggest
that when server load is not an issue, mutual authen-
tication should be used. For a resource constrained
server, on the other hand, the use of elliptic curve op-
erations may still allow for two-way authentication,
that could not take place anymore when RSA based
methodas are used.
6 CONCLUSIONS
We have performed a thorough examination of the
TLS handshake with a focus on the number of mes-
sages exchanged in relation to the chosen cipher-
suites. Especially in the context of constrained, mo-
bile or embedded devices, the number of messages
that has to be transmitted to setup a secure connection
can have a huge impact on the performance and life-
time of the single appliances. We then observed the
influence of higher security on the number of mes-
sages and on the load put on the participating par-
ties. Our results indicate that elliptic curve cryptog-
raphy is not only useful for this special environment
due to the smaller memory requirements, but also that
the increase in load put on the parties when the secu-
rity of the connection is heightened, through mutual
authentication or the usage of ephemeral variants of
the Diffie-Hellman protocol, is significantly smaller
when compared to its RSA/DSA counterparts. Future
research will now try to bring down the required mes-
sages to a bare minimum without sacrificing integrity
or authenticity of the connection.
ACKNOWLEDGEMENTS
The authors are supported by the MA27 - EU-
Strategie und Wirtschaftsentwicklung - in the course
of the funding programme Stiftungsprofessuren und
Kompetenzteams f
¨
ur die Wiener Fachhochschul-
Ausbildungen.
REFERENCES
Blake-Wilson, S., Bolyard, N., Gupta, V., Hawk, C., and
Moeller, B. (2006a). RFC 4492: Elliptic Curve Cryp-
tography (ECC) Cipher Suites for Transport Layer Se-
curity (TLS). Technical report, The Internet Society.
Blake-Wilson, S., Nystrom, M., Hopwood, D., Mikkelsen,
J., and Wright, T. (2006b). RFC 4366: Transport
Layer Security (TLS) Extensions. Technical report,
The Internet Society.
Dierks, T. and Rescorla, E. (2006). RFC 4346: The Trans-
port Layer Security (TLS) Protocol Version 1.1. Tech-
nical report, The Internet Society.
Gupta, V., Gupta, S., Chang, S., and Stebila, D. (2002). Per-
formance Analysis of Elliptic Curve Cryptography for
SSL. In Workshop on Wireless Security - Proceedings
of the 1st ACM workshop on Wireless security, pages
87–94. ACM.
Hankerson, D., Menezes, A., and Vanstone, S. (2004).
Guide to Elliptic Curve Cryptography. Springer Pro-
fessional Computing. Springer-Verlag New York.
Koschuch, M., Hudler, M., Kr
¨
uger, M., Großsch
¨
adl, J.,
and Payer, U. (2008). Workload Characterization of
a Lightweight SSL Implementation Resistant to Side-
Channel Attacks. In Franklin, M. K., Hui, L. C. K.,
and Wong, D. S., editors, Cryptology and Network
PERFORMANCE EVALUATION OF THE TLS HANDSHAKE IN THE CONTEXT OF EMBEDDED DEVICES
41

Security, 7th International Conference, CANS 2008,
Proceedings, volume 5339 of Lecture Notes in Com-
puter Science, pages 349–365, Hong Kong, China.
Springer Verlag. 02.-04. December 2008.
Koschuch, M., Lechner, J., Weitzer, A., Großsch
¨
adl,
J., Szekely, A., Tillich, S., and Wolkerstorfer, J.
(2006). Hardware/Software Co-Design of Elliptic
Curve Cryptography on an 8051 Microcontroller. In
L. Goubin and M. Matsui (Eds.): CHES 2006, pages
430–444.
Krasner, J. (2004). Using Elliptic Curve Cryptography
(ECC) for Enhanced Embedded Security - Finan-
cial Advantages of ECC over RSA or Diffie-Hellman
(DH).
Lederer, C., Mader, R., Koschuch, M., Großsch
¨
adl, J.,
Szekely, A., and Tillich, S. (2009). Energy-Efficient
Implementation of ECDH Key Exchange for Wireless
Sensor Networks. In Workshop in Information Secu-
rity Theory and Practices (WISTP’09), volume 5746
of Lecture Notes in Computer Science, pages 112–
127, Brussels, Belgium. Springer-Verlag New York.
01.-04. September 2009.
Lenstra, A. K. and Verheul, E. R. (2001). Selecting Cryp-
tographic Key Sizes. Journal of Cryptology: the jour-
nal of the International Association for Cryptologic
Research, 14(4):255–293.
Potlapallyy, N. R., Raviy, S., Raghunathany, A., and Lak-
shminarayanaz, G. (2002). Optimizing Public-Key
Encryption for Wireless Clients. In Communications,
2002. ICC 2002. IEEE International Conference on,
volume 2, pages 1050 – 1056.
Ravi, S., Raghutan, A., and Potlapally, N. (2002). Securing
Wireless Data: System Architecture Challenges. In
ISSS 02.
DCNET 2010 - International Conference on Data Communication Networking
42

APPENDIX
Table 1: Number of High-Level Cryptographic Operations performed by the Server during SSL/TLS-Handshake. Numbers
behind “/” indicate mutual authentication.
Server
Key Exchange # of
Messages
RSA
Encryption
RSA
Decryption
Exponenti-
ation
DSS Sig
Generation
DSS Sig
Verification
Scalar
Multiplication
ECDSA Sig
Generation
ECDSA Sig
Verification
DH anon 4 2
DH DSS 4/5 1 0/1
DH RSA 4/5 0/1 1
DHE DSS 5/6 2 1 0/1
DHE RSA 5/6 1 0/1 2
RSA 4/5 1 0/1
ECDH anon 4 2
ECDH ECDSA 4/5 1 0/1
ECDH RSA 4/5 0/1 1
ECDHE ECDSA 5/6 2 1 0/1
ECDHE RSA 5/6 1 0/1 2
Table 2: Number of High-Level Cryptographic Operations performed by the Client during SSL/TLS-Handshake. Numbers
behind “/” indicate mutual authentication.
Client
Key Exchange # of
Messages
RSA
Encryption
RSA
Decryption
Exponenti-
ation
DSS Sig
Generation
DSS Sig
Verification
Scalar
Multiplication
ECDSA Sig
Generation
ECDSA Sig
Verification
DH anon 3 2
DH DSS 3/5 2 0/1 1
DH RSA 3/5 0/1 1 2
DHE DSS 3/5 2 0/1 2
DHE RSA 3/5 0/1 2 2
RSA 3/5 1 0/1 1
ECDH anon 3 2
ECDH ECDSA 3/5 2 0/1 1
ECDH RSA 3/5 0/1 1 2
ECDHE ECDSA 3/5 2 0/1 2
ECDHE RSA 3/5 0/1 1 2
Table 3: Cycle count for the server when one-way authentication is used, normalized so that a modular exponentiation with a
16-bit exponent needs a count of one.
Server one-way
Key Exchange # of
Messages
RSA
Encryption
RSA
Decryption
Exponenti-
ation
Scalar
Multiplication
ECDSA Sig
Generation
ECDSA Sig
Verification
Total
DH anon 4 32 32
DH RSA 4 16 16
DHE RSA 5 1 32 33
RSA 4 34 34
ECDH anon 4 6 6
ECDH ECDSA 4 3 3
ECDH RSA 4 3 3
ECDHE ECDSA 5 6 4 10
ECDHE RSA 5 1 6 7
PERFORMANCE EVALUATION OF THE TLS HANDSHAKE IN THE CONTEXT OF EMBEDDED DEVICES
43

Table 4: Cycle count for the server when mutual authentication is used, normalized so that a modular exponentiation with a
16-bit exponent needs a count of one.
Server mutual
Key Exchange # of
Messages
RSA
Encryption
RSA
Decryption
Exponenti-
ation
Scalar
Multiplication
ECDSA Sig
Generation
ECDSA Sig
Verification
Total
DH RSA 5 34 16 50
DHE RSA 6 1 34 32 67
RSA 5 34 34
ECDH ECDSA 5 3 4 7
ECDH RSA 5 34 3 37
ECDHE ECDSA 6 6 4 4 14
ECDHE RSA 6 1 34 6 42
Table 5: Cycle count for the client when one-way authentication is used, normalized so that a modular exponentiation with a
16-bit exponent needs a count of one.
Client one-way
Key Exchange # of
Messages
RSA
Encryption
RSA
Decryption
Exponenti-
ation
Scalar
Multiplication
ECDSA Sig
Generation
ECDSA Sig
Verification
Total
DH anon 3 1 1
DH RSA 3 34 1 35
DHE RSA 3 69 1 69
RSA 3 1 1
ECDH anon 3 6 6
ECDH ECDSA 3 6 4 11
ECDH RSA 3 34 6 41
ECDHE ECDSA 3 6 9 15
ECDHE RSA 3 34 6 41
Table 6: Cycle count for the client when mutual authentication is used, normalized so that a modular exponentiation with a
16-bit exponent needs a count of one.
Client mutual
Key Exchange # of
Messages
RSA
Encryption
RSA
Decryption
Exponenti-
ation
Scalar
Multiplication
ECDSA Sig
Generation
ECDSA Sig
Verification
Total
DH RSA 5 1 34 1 36
DHE RSA 5 1 69 1 70
RSA 5 1 1
ECDH ECDSA 5 6 4 4 14
ECDH RSA 5 1 34 6 42
ECDHE ECDSA 5 6 4 9 18
ECDHE RSA 5 1 34 6 42
DCNET 2010 - International Conference on Data Communication Networking
44