EFFICIENT ALGORITHMIC SAFETY ANALYSIS OF HRU

SECURITY MODELS

∗

Anja Fischer and Winfried K¨uhnhauser

Ilmenau University of Technology, Ilmenau, Germany

Keywords:

Security engineering, Security policies, Security models, Access control, HRU safety, Model decomposition,

Enterprise resource planning security.

Abstract:

In order to achieve a high degree of security, IT systems with sophisticated security requirements increasingly

apply security models for specifying, analyzing and implementing their security policies. While this approach

achieves considerable improvements in effectiveness and correctness of a system’s security properties, model

speciﬁcation, analysis and implementation are yet quite complex and expensive.

This paper focuses on the efﬁcient algorithmic safety analysis of HRU security models. We present the theory

and practical application of a method that decomposes a model into smaller and autonomous sub-models

that are more efﬁcient to analyze. A recombination of the results then allows to infer safety properties of

the original model. A security model for a real-world enterprise resource planning system demonstrates the

approach.

1 INTRODUCTION

IT systems with advanced security requirements in-

creasingly apply problem-speciﬁc security policies

for describing, analyzing and implementing secu-

rity properties (Bryce et al., 1997; Halfmann and

K¨uhnhauser, 1999; Loscocco and Smalley, 2001; Ef-

stathopoulos and Kohler, 2008). In order to precisely

describe security policies, formal security models

such as (Harrison et al., 1976; Goguen and Meseguer,

1982; Brewer and Nash, 1989; Sandhu et al., 1996)

are applied, allowing for formal analyses of secu-

rity properties and serving as speciﬁcations from

which policy implementations are generated (Vimer-

cati et al., 2005).

While security policies and their formal models

achieve considerable improvements in effectiveness

and correctness of a system’s security properties, the

costs of this approach often are rather forbidding. The

analysis of security models is often pestered by com-

putational complexity, making it difﬁcult to devise al-

gorithms for automated analysis tools.

A fundamental motivation for access control se-

curity models is to study the proliferation of access

rights. This problem was formalized in HRU access

control models in order to ﬁnd proliferation bound-

aries and to prove that, for a given security model,

∗

This work is partially supported by Carl-Zeiss-Stiftung.

these boundaries will never be crossed – a security

property known as HRU safety.

Unfortunately, HRU safety turned out to be unde-

cidable for models written in the general HRU calcu-

lus, making it difﬁcult to devise algorithms for auto-

mated safety analysis tools. As a consequence, sev-

eral safety-decidable fragments of the HRU calcu-

lus emerged (Harrison and Ruzzo, 1978; Lipton and

Snyder, 1978; Ammann and Sandhu, 1991; Sandhu,

1992) that bought safety decidability by limiting the

expressivepower of the calculus. Unfortunately,these

fragments now result in another drawback: they often

show severe limitations in their power to model the

complex policies of larger real-world systems. Con-

sequently, the chances for automated safety analyses

of real-world security models are quite low.

In this paper, we propose a method for analyz-

ing the safety properties of unrestricted HRU security

models. Although the safety problem is still gener-

ally pestered by undecidability, the method achieves

results in many practical cases. The core of the idea

is to decompose a model into smaller sub-models,

then analyze these sub-models individually and re-

combine the results – an approach also applied in the

analysis of complex automata (Krohn and Rhodes,

1965). The rationale behind this approach is twofold.

Firstly, smaller sub-models can be analyzed more ef-

ﬁciently by heuristic safety analysis algorithms with

Fischer A. and Kühnhauser W. (2010).

EFFICIENT ALGORITHMIC SAFETY ANALYSIS OF HRU SECURITY MODELS.

In Proceedings of the International Conference on Security and Cryptography, pages 49-58

DOI: 10.5220/0002986600490058

 SciTePress

polynomial or exponential runtimes. Secondly, be-

cause sub-models can be analyzed independently the

parallelism of multi-core processor architectures can

be exploited.

The contributions of this paper are a formal deﬁni-

tion of the decomposition method and a formal proof

of its correctness. Throughout the paper, excerpts

from a real-world enterprise resource planning system

security policy illustrate the details.

2 RELATED WORK

Fundamental to this paper is the work of Harrison et

al. (Harrison et al., 1975; Harrison et al., 1976). The

authors present a calculus to formalize access con-

trol policies, consisting of access control matrices and

state machines. The primary purpose of security mod-

els written in the HRU calculus is to obtain statements

about the proliferation of access rights, drawn from

a reachability analysis of the model’s state machine.

As was to be expected, the HRU safety problem – the

property whether a given right may appear in some

future automaton state – turned out to be undecid-

able for general HRU models, and work focused on

ﬁnding fragments of the HRU calculus with decid-

able safety properties. It was proved that the safety

problem is decidable, e.g. for mono-operational (Har-

rison et al., 1976) and mono-conditional (Harrison

and Ruzzo, 1978) HRU models. Lipton and Snyder

(Lipton and Snyder, 1978) introduced static restric-

tions on subject creation. Sandhu proposed the typed

access matrix model (TAM) (Sandhu, 1992) that aug-

mented the HRU model by a type system.

Kleiner and Newcob (Kleiner and Newcomb,

2006; Kleiner and Newcomb, 2007) present an access

control model that improves the ability to deal with

the absence of permissions but can still simulate any

HRU model. The authors also present different and

more rigorous terms of safety properties showing that

they can be decided. In (Kleiner and Newcomb, 2007)

the safety access temporal logic is introduced, which

is able to express a variety of safety properties over

access control models and is interpreted over ﬁnite

runs of the access control system. The model check-

ing problem for the entire logic is undecidable; again,

a fragment of the logic was identiﬁed for which the

problem is decidable. The HRU safety problem can

be reduced to this fragment in some cases.

Li et al. (Li et al., 2005) argue that delegation

of rights is a useful feature of access control systems

while it makes safety and security analyses more im-

portant. The authors present a trust management lan-

guage in the RT family (role-based trust-management

languages) which can be encoded in the HRU model

but is more application-oriented. The authors deﬁne

the goals of a security analysis in more general terms

such as simple safety, simple availability or mutual

exclusion and show that they can be decided.

Our approach to HRU safety analysis differs from

these approaches in a fundamental way. Instead of in-

troducing model restrictions our safety analysis tech-

nique works on the original, general HRU calculus

(and, of course, its derivatives) and aims at a practical

method for dealing with the problem’s computational

complexity. We tackle the problem by decomposing a

model into smaller sub-models, analyzing the safety

properties of the sub-models and providing a tech-

nique to carry the analysis results back to the origi-

nal model. The basic ideas of this approach originate

from the decomposition of automata and go back to

(Krohn and Rhodes, 1965).

3 APPLICATION SCENARIO

The challenges addressed in this paper are motivated

by the complexity of the security requirements in

real-world application scenarios. In this section, we

dedicate some space to introduce a security-sensitive,

real-world application system to motivate a set of

application-speciﬁc security requirements. Based on

these requirements we proceed with composing an in-

formal security policy that then motivates the secu-

rity model in Section 4. The application scenario,

the security policy and its model will then provide a

background, an example and a source of arguments

throughout the rest of the paper.

We do this in some detail, because the subsequent

model decomposition technique in Section 5 injects

human application knowledge into the safety analysis

algorithms as one means to reduce their runtime, and

thus this knowledge should be available to the reader.

3.1 Application

The application scenario is a distributed enterprise

collaboration system providing services that efﬁ-

ciently extend business processes of cooperating or-

ganizations across company boundaries. We espe-

cially focus on standard business systems (such as en-

terprise resource planning (ERP) systems) supporting

logistic business processes for cooperative order pro-

cessing.

One important task in this scenario is the process

of availability checking (available-to-promise, ATP)

which is a typical business process that crosses sev-

eral company boundaries whenever sub-contractors

SECRYPT 2010 - International Conference on Security and Cryptography

Figure 1: Application scenario.

are involved. When customers place orders with man-

ufacturers that use ERP systems, these ERP systems

call ATP services of further suppliers for checking

the availability of outside supplied original equipment

manufacturer (OEM) parts (Fig. 1). ATP services of-

ten are implemented as web services, and thus a man-

ufacturer generally has to call several web services of

different OEM suppliers for processing a single order.

In our example, this service (among other web ser-

vices) is provided by a service provider on a shared

communication platform. Once the ATP web service

has received a manufacturer’s availability request, the

ATP service forwards the request to all the manufac-

turer’s OEM part suppliers, analyses the responses

and sends the results back to the ERP system. The

ERP system evaluates the suppliers’ responses which

then results in an offer for the customer.

3.2 Security Requirements

In cross-company business processes, common secu-

rity properties such as conﬁdentiality, integrity, avail-

ability, authenticity, and non-repudiation are both

self-evident as well as essential. This section dis-

cusses two application-speciﬁc key requirements.

One key requirement in this scenario is the sep-

aration of duty between administrators and regular

users. This means, regular users may only obtain reg-

ular (operative) permissions and administrators may

solely possess administrator permissions.

Delegation of rights — temporarily entrusting a

user’s access rights to another user — is a common

feature of business applications. Due to the collabo-

ration system’s properties of providing services to in-

dependent companies, the second key requirement is

to restrict delegationof rights to company boundaries.

Consequently, rights may only be delegated between

users acting on behalf of the same company.

3.3 Authorization Policy

Any security policy is a set of rules designed to

meet the security goals of an IT system (Common3.1,

2009). While security policies in general include

rules about authentication or communication, the dis-

cussion in this paper focuses on the core part of a

policy, the authorization rules. Especially, this sub-

section discusses an informal authorization policy for

the example scenario outlined in the previous section.

The next section will then rewrite this policy as a for-

mal HRU security model.

The authorization policy is an immanent part of

the service provider’ssecurity policy and, as such, it is

integrated into the service provider’s shared commu-

nication platform. It contains access control rules for

all references to web services

made by users. Thus,

whenever a user tries to call a web service, the au-

thorization policy’s rules are applied to grant or deny

access.

In order to enforce separation of duty, the autho-

rization policy differentiates between regular and ad-

ministrative rights; a user’s right to obtain permis-

sions results from his identity. Among others, the au-

thorization policy contains rights to execute a web ser-

vice and to delegate and revoke this right. The rights

delegate and revoke realize a user-based grant dele-

gation (Crampton and Khambhammettu, 2008) sup-

porting a one-level delegation hierarchy. Note that the

application scenario may also support a n-level dele-

gation hierarchy; however, due to demonstrating pur-

poses of the decomposition algorithm we reduce the

application scenario to the basics.

In order to implement rights delegation restricted

to company boundaries, users from different compa-

nies must be distinguished by adopting the concept of

security domains of non-interference security models

(Goguen and Meseguer, 1982). Hence, to deﬁne del-

egation boundaries, each user is assigned a security

domain. Users of a company belong to the same se-

curity domain, and users belonging to different com-

panies belong to different security domains.

In summary, the authorization policy contains –

among others – the following rules:

1. Every user is assigned one of two mutually exclu-

sive user types: regular user or administrator.

2. The user types’ rights sets are disjoint. Regular

rights are execute, delegate, and revoke. Admin-

istrative rights are rights to manage the authoriza-

tion policy.

3. In order to delegate a right, delegator and delega-

tee must belong to identical security domains.

4. Delegation of rights is additive — both delegator

and delegatee possess the delegated rights.

Note that there are different object types, e.g. web ser-

vices, administration operations, and rights. Due to con-

ciseness we only consider web services in the following.

EFFICIENT ALGORITHMIC SAFETY ANALYSIS OF HRU SECURITY MODELS

4 SECURITY MODEL

While security policies generally are phrased in natu-

ral language, systems with advanced security require-

ments increasingly apply security models for formal

description and rigorous analysis of their security

properties. Most of the existing models address spe-

ciﬁc challenges: to prove the mapping from an ab-

stract design level (such as information ﬂow graphs)

to a system oriented level (such as access control

mechanisms (Bell and LaPadula, 1973)), to prove in-

terference rules for security domains (Goguen and

Meseguer, 1982), or to precisely deﬁne role contain-

ment (Sandhu et al., 1996) or information ﬂow (Efs-

tathopoulos and Kohler, 2008).

In large real-world applications, a major challenge

is controlling the proliferation of rights. Particularly

in distributed systems shared by independent organi-

zations (such as the ERP example), questions such as

”Is it possible that users belonging to some organiza-

tion A may, at some point in the future, get access to

internal information of users from organization B?”

arise. The analysis of such dynamic right prolifera-

tion is the primary objective of HRU security models

and is known as the HRU safety problem (Harrison

et al., 1975; Harrison et al., 1976).

In order to model dynamic behavior of access con-

trol systems, any HRU security model is a state ma-

chine deﬁned by a tuple (Q, Σ,δ,q

) with a state set

Q, an input alphabet Σ, a state transition function δ

and an initial state q

. Any state q ∈ Q is a snapshot

of the system’s access control matrix (ACM) and is

modeled by a triple (S,O,m) where S is a set of sub-

jects, O is a set of objects, and m : S× O → 2

is an

access control matrix where the cells contain subsets

of a ﬁnite right set R.

Security properties can now be analyzed by ob-

serving state transitions; in particular, statements

about right proliferation can be made by state reach-

ability analysis. Safety analysis in HRU models fo-

cuses on a fundamental family of questions: Given

some state (an ACM), is it possible that a speciﬁc sub-

ject ever obtains a speciﬁc permission with respect to

a speciﬁc object? Or, in other words, given a state q, is

it possible that in some future state q

′

= δ

∗

(q,a) a spe-

ciﬁc right r leaks into a matrix cell? If this may hap-

pen, such states are not considered safe with respect to

r. Precisely, given an HRU security model and a right

r, a state q is called safe wrt. r iff∀s ∈ S,o∈ O,a ∈ Σ

∗

r /∈ m(s,o) ⇒ r /∈ m

′

(s,o) withq

′

= δ

∗

(q,a)

(Harrison et al., 1975; Harrison et al., 1976).

Following the policy outlined in Section 3.3, we

now will look into the corresponding HRU model; its

safety properties will afterwards be analyzed in Sec-

tion 5.

In our ATP scenario, the set of subjects S = {s

|i ∈

N} represents the application’s users, whereas the set

of objects O = {o

| j ∈ N} describes the methods of

the web services. M = {m|m : S × O → 2

} repre-

sents the set of access control matrices. Each matrix

m ∈ M speciﬁes the rights each user (subject) has with

respect to each web service method (object).

The set R models rights that subjects may own on

objects. In the ERP scenario, users may own rights

to execute web service methods (executeWSMethod

to delegate and revoke rights to execute methods

(delegateExecuteRight

, revokeExecuteRight

), or to

perform system administration operations such as

user, or service management.

Model dynamics are deﬁned by the transition

function δ : Q × Σ → Q that reﬂects the rules which

prescribe the authorization for making incremental

changes to the protection state in the ACM (thus δ is

often called the model’s authorization scheme). Σ is

the ﬁnite set of inputs coveringall application-speciﬁc

operations that result in a modiﬁcation of the model

state. In real-world applications, operations in Σ typi-

cally (but not exclusively) are used by security admin-

istrators and eventually involve users, web services,

and other parameters. For example the operation cre-

ateUser called in some state q = (S

) adds a

new subject to S

; here, parameters are the caller (an

administrator) and the subject to be created. Precisely,

the input set Σ is a tuple consisting of

• the set of operations that affect the model state

(such as createUser, delegateExecuteRight)

• the parameters of these operations, consisting of

subjects and objects.

Fig. 2 gives a small example for the deﬁnition

of a model state transition caused by the operation

delegateExecuteRight.

δ(q,(delegateExecuteRight,s

,o)) ::=

if delegateExecuteRight

∈ m(s

,o)

and executeWSMethod

∈ m(s

,o)

and dom(s

) ∈ m(s

dom

)

then

enter executeWSMethod

into m(s

,o)

end if.

Figure 2: Authorization scheme for delegateExecuteRight.

delegateExecuteRight

grants delegator s

per-

mission to delegate the right executeWSMethod

delegatee s

. The rationale is that if s

owns

executeWSMethod

and is a member of the same se-

curity domain as s

, then the state machine moves into

SECRYPT 2010 - International Conference on Security and Cryptography

a new state in which the access matrix contains the

right executeWSMethod

for the subject s

with re-

spect to the web service method o.

With respect to the pure HRU calculus, we meet

with an unfamiliar concept in Fig. 2: we used a func-

tion dom where an access right should be expected.

Although a little off from the core intentions of this

section – to sketch an HRU model for an ATP system

– we nevertheless want to comment on the validity of

doing so.

While from a theoretical point of view the HRU

calculus has sufﬁcient expressive power to model any

computable policy, from a modeler’s point of view the

rules of a policy do not always map elegantly to the

calculus’ abstractions. As an example, while the se-

curity policy outlined in Section 3.3 uses security do-

mains in order to isolate different organizations, HRU

model states consist of simple ACMs only. We deal

with this problem in the following way.

We describe the security domains deﬁned on the

policy level by a ﬁnite set D, and the association of

any user to a security domain by a function dom :

S → D. Because any function can also be written

as a mapping table, we now can express dom using

the abstractions of the HRU calculus by adding a new

column for a virtual object o

dom

to the access con-

trol matrix, in which each domain is represented by

a corresponding “right”. Thus by extending the set R

to R ∪ D and the set O to O∪ {o

dom

}, a test whether

two users s

and s

are members of the same domain

maps to dom(s

) ∈ m(s

dom

), and the use of the

dom-function in the condition part of state transition

deﬁnition becomes legitimate.

Back to modeling the security policy from Sec-

tion 3.3. Two issues remain to complete the model:

modeling the fact that a subject is a security admin-

istrator, and the deﬁnition of the initial model state.

The requirement from Section 3.2 to differentiate be-

tween regular users and administrators is met by mod-

eling an authority compartment: admin. We start the

model in the initial state q

= (S

) with one

administrator, resulting in an initial set of subjects

= {administrator}. Using the same trick as when

modeling the dom function, the association of sub-

jects to the authority compartment is modeled by a

virtual right admin

which manifests in an extra ma-

trix column for a virtual object o

comp

. Thus the initial

object set is O

= {o

comp

}. The initial matrix m

con-

sists of a single row for administrator, and a single

column for the compartment association represented

by the virtual object o

comp

(Fig. 3), and the model is

complete.

Concluding, this section has sketched major com-

ponents of a security model for the policy outlined

Figure 3: Initial access matrix m

in Section 3.3 by applying the general HRU calculus,

syntactically enriched by calculus-consistent compo-

nents for modeling administrative users and security

domains. The complete model including the deﬁ-

nition of all model sets, the complete authorization

scheme encompassing about ten administrative opera-

tions, and the deﬁnition of the initial model state con-

sists of approximately 140 lines in the HRU calculus

and took about 16 hours to set up. As a result, we

now have a solid foundation for a formal analysis of

the security properties and especially the safety prop-

erties of our policy.

5 SAFETY ANALYSIS

In this section, we propose a model decomposition

method for unrestricted HRU security models that, al-

though still generally pestered by safety undecidabil-

ity, allows for safety analysis in many practical cases.

The core of the method is to decompose a model into

smaller sub-models, then analyze these sub-models

individually and recombine the results.

5.1 Model Decomposition

Model decomposition divides the state space of an

HRU model (the ACM) into two or more smaller and

disjoint slices. Each slice differs from the original

ACM in that either its subject set, its object set or both

are smaller. By maintaining the authorization scheme

δ, the input set Σ and (accordingly restricted) the ini-

tial state q

, two or more sub-models with reduced

state spaces emerge.

Just decomposing a model into smaller slices does

of course not reduce the inherent complexity of solv-

ing the safety problem. The underlying idea is a dif-

ferent one.

Firstly, because the safety problem is generally

undecidable, we have to resort to heuristics-based

safety analysis algorithms with runtime boundaries

typically depending polynomially or exponentially on

the size of the model’s state space. As an exam-

ple, for a state space size s and an analysis algorithm

running in O(s

), a state space reduction by a factor

of four (model decomposition into four equally-sized

sub-models), the runtime of the algorithm is bounded

by 4(s/4)

= 1/4 s

, which for manageable values of

s makes a huge difference to s

. Because sub-models

EFFICIENT ALGORITHMIC SAFETY ANALYSIS OF HRU SECURITY MODELS

are independent and thus can be analyzed simulta-

neously on multi-core/multiprocessor/grid architec-

tures, the runtime actually is bounded by 1/16s

Secondly, the success of heuristic safety analy-

sis algorithms largely depends on the quality of the

heuristics, and here we take the view that the use

of human problem knowledge is a quality source for

guiding heuristics-based algorithms. The challenge

here is ﬁnding a problem-speciﬁc model decomposi-

tion that minimizes the state spaces of the sub-models

without violating model semantics. On the one hand,

a necessary condition for any valid state decomposi-

tion is that the resulting slices still are closed with re-

spect to the model’s authorization scheme δ. On the

other hand, a proper heuristics will strive to maximize

the number of resulting slices.

Before precisely deﬁning what is meant by closed

with respect to δ, let us ﬁrst brieﬂy look at our exam-

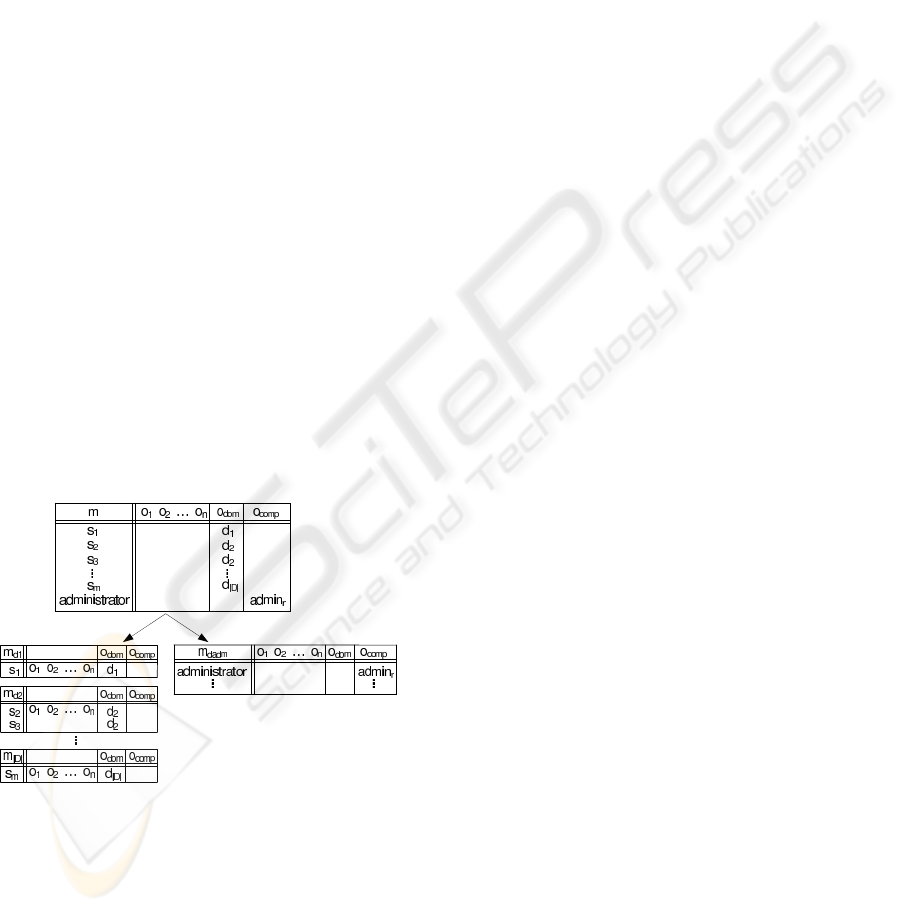
ple from Section 4. For cross-company scenarios, an

obvious decomposition heuristics exploits the natu-

ral security domains deﬁned by the company perime-

ters: each sub-model then covers the state of exactly

one individual domain. With D denoting the set of

domains, this example results in |D| self-contained

sub-models with |D| pairwise disjoint subject sets

...S

|D|

, a common object set O, and |D| matrix

slices m

that contain only the rows for their individ-

ual subject sets S

. Additionally, prominent subjects

not directly associated to any security domain (such

as security administrators) are collected in a separate

slice m

adm

(Fig. 4).

Figure 4: State space decomposition.

Note that in each sub-model only the access matri-

ces differ. The right sets, the rights in the matrix cells

and the authorization schemes of the sub-models ex-

actly match their counterparts in the original model.

Now let us consider the properties of a proper

model decomposition. Given an HRU model

(Q,Σ, δ,q

), any decomposition heuristics d decom-

poses the state space Q = 2

× 2

× M into two or

more state spaces Q

of sub-models (Q

,Σ, δ

where

- Q

= 2

× 2

× M

⊆ S, O

⊆ O,M

= {m|m :

× O

→ 2

}

- δ

(q|Q

,a) = δ(q,a)|Q

for q ∈ Q and a ∈ Σ

- q

= q

The expression ”q|Q

” denotes the restriction of a

state q ∈ Q to a smaller state in the state space Q

some sub-model. Precisely, q|Q

= (S|S

,O|O

,m|M

)

removes those parts of a state q that are not within

the sub-model’s deﬁnition domain. In the state

space decomposition in Fig. 4, a state q of the full

model is ({s

...administrator},{o

...o

comp

},m), and

q|Q

adm

= ({administrator} , {o

...o

comp

},m

adm

Because our goal is to infer safety properties of the

original model from individual safety properties of

its sub-models, any model decomposition must have

distinct properties: each individual sub-model must

be an autonomous HRU model, and the set of sub-

models collectively must exhibit exactly the same be-

havior as the original model. We will look into sub-

model autonomy and behavior equivalence in the next

subsections.

5.1.1 Sub-model Autonomy

In order to be an autonomous HRU model, each sub-

model’s state space Q

must be closed with respect to

its δ

. Closedness means that, for each state q of the

original model, if q is restricted to the state space Q

of the sub-model, each state reachable from q in the

original model by applying δ still is in Q

Def. State Closedness. In any HRU model

(Q,Σ, δ,q

), a subset Q

⊂ Q is called state-

closed iff ∀q ∈ Q, a ∈ Σ : q ∈ Q

⇒ δ(q,a) ∈ Q

5.1.2 Sub-model Isomorphism

In order to infer safety properties of the original

model from the set of sub-models, any model decom-

position must preserve the structure as well as the be-

havior of the original model. In other words, a model

decomposition d must be an isomorphism.

To this end, for any model decomposition into n

sub-models d must induce a complete decomposition

of the state space Q such that

i=1

= Q (denoting

that

i=1

× O

) = (S × O)). Any good decompo-

sition will also avoid redundancies in the sub-models

and induce mutually disjoint state spaces, ∀i, j,i 6= j :

∩ Q

0 (denoting that (S

× O

) ∩ (S

× O

) =

0).

These properties are summarized in the following

deﬁnition.

Def. Model/Sub-model Isomorphism. Given

an HRU model (Q,Σ,δ,q

), a function

SECRYPT 2010 - International Conference on Security and Cryptography

d : d(Q) 7→ (Q

...Q

) is called a decomposi-

tion function iff

(a) each Q

is state-closed

(b)

i=1

= Q (completeness)

∩ Q

0 (mutual disjointness)

(d) ∀q ∈ Q,a ∈ Σ : δ

(q|Q

,a) = δ(q, a)|Q

with Q

as deﬁned above.

Intuitively, sub-models are autonomous HRU

models, sharing the authorization scheme with their

origin but having smaller state spaces. The n sub-

models generated by d establish a set of n smaller

HRU models with state spaces Q

...Q

, the sub-

model set collectively implementing a virtual state

transition function δ : Q

× ... × Q

× Σ → (Q

...Q

δ(q

,..., q

,a) 7→ (δ

,a),..., δ

,a)) with δ

deﬁned in (d). The properties (b) and (c) of the

state space decomposition function d now imply that

there exists a state decomposition function d : Q →

× ... × Q

, d(q) 7→ (q|Q

,..., q|Q

) that selects the

partial states q

for each sub-model (Fig 5).

Because of (a), (b) and (c), d is a homomorphism

from Q to Q

...Q

, and d(δ(q,a)) = δ(d(q), a) holds

because of (d) (Fig. 6). Because of (b) and (c), d

is also bijective, and the inverse mapping d

−1

: Q

... × Q

→ Q exists which recombines the result of

the sub-model’s state transitions by d

−1

...q

) 7→

i=i

. Thus d is also an isomorphism, and δ(q,a) =

−1

(δ(d(q), a)) holds, which ﬁnally shows that the

original model and the set of its sub-models generated

by a proper decomposition function d are isomorphic.

Figure 5: State decomposition function d.

Figure 6: State decomposition isomorphism.

5.1.3 Discussion

The deﬁnition of state closedness opens a wide variety

of decomposition patterns. In fact, ﬁnding a decom-

position heuristics that matches the closedness prop-

erties is exactly the intellectual challenge that tack-

les the problem of computational complexity inherent

to fully automated safety analysis. In the past, vari-

ous ACM decompositions such as our own example

(Fig. 4), or decompositions into single matrix rows or

columns have been successfully applied in different

areas. For example, the single row/column decompo-

sitions resulted in efﬁcient implementations of ACMs

by ACLs respectively capability lists.

We already sketched the results of applying the

decomposition method to the security model of our

application scenario in Fig. 4. Assuming that the se-

curity model consists of |D| security domains and ap-

plying a decomposition heuristics based on these do-

mains, we obtain |D|+1 sub-models where each sub-

model is an autonomous HRU model, and each but

one model satisﬁes the closedness condition.

The rogue sub-model is unique in that it contains

only users belonging to the authority compartment

admin

but not to any security domain. At this point,

readers already might have observed that this sub-

model does not satisfy sub-model closedness, because

administrative users are able to affect any other sub-

model, e.g. by granting rights to subjects. However,

these are desirable characteristics since, being respon-

sible for policy management, administrative users are

trustworthy by deﬁnition. Furthermore, analyzing a

model’s safety properties in consideration of admin-

istrative users is a trivial problem because they are

usually able to proliferate any right in any state and

thus are unspectacular with respect to safety analy-

sis. Their collection in a single, unsafe sub-model

purges administrative contaminations from all other

sub-models and allows for a pure safety analysis re-

stricted to regular users.

5.2 From Sub-model Safety to Model

Safety

It remains to show that safety properties of an HRU

model are maintained by a decomposition. Before we

discuss a corresponding theorem, we set up a lemma

about the equivalence of δ and the δ

’s of the sub-

models.

Lemma (δ

∗

-equivalence). Let δ

∗

: Q × Σ

∗

→ Q be

the extension of δ to a sequence of inputs from

∗

. Then, given an HRU model (Q, Σ,δ,q

) and

a decomposition function d, ∀a ∈ Σ

∗

, q ∈ Q a sub-

model (Q

,Σ, δ

) exists such that δ

∗

(q,a)|Q

∗

(q|Q

,a).

This follows directly from the state closedness of

the Q

’s and the deﬁnition of the δ

’s, because each

sees exactly the same local state as its original and

thus performs the same state transitions.

Theorem (Sub-model Safety Equivalence). Given

EFFICIENT ALGORITHMIC SAFETY ANALYSIS OF HRU SECURITY MODELS

an HRU model (Q,Σ,δ, q

) and a decomposition

function d. Then, ∀q ∈ Q,r ∈ R :

q not safe wrt. r ⇔ ∃ sub-model(Q

,Σ, δ

) : q|Q

not safe wrt. r.

Proof.

”⇒”:

q = (S,O,m) not safe wrt. r

⇒ ∃ s ∈ S,o ∈ O,a ∈ Σ

∗

′

∈ Q,

′

= δ

∗

(q,a) = (S

′

) :

r /∈ m(s,o) ∧ r ∈ m

′

(s,o).

Because d is complete and disjoint, there exists

exactly one sub-model (Q

,Σ, δ

) containing

the critical matrix cell: m(s,o) = m

(s,o) where

s ∈ S

,o ∈ O

Because of the δ

∗

-equivalence lemma,

′

)|Q

= q

′

= δ

∗

(q,a)|Q

= δ

∗

(q|Q

,a) = q

′

= (S

′

⇒ m

′

= m

′

Because s ∈ S

and o ∈ O

⇒ m(s,o) = m

(s,o) and m

′

(s,o) = m

′

(s,o).

Because r /∈ m

(s,o) ∧ r ∈ m

′

(s,o), (Q

,Σ, δ

)

is a sub-model where q

= q|Q

is not safe wrt. r.



”⇐”:

∃ sub-model (Q

,Σ, δ

) : q|Q

not safe wrt. r;

then, with q

= q|Q

= (S

)

⇒ ∃s ∈ S

,o ∈ O

,a ∈ Σ

∗

′

= δ

∗

,a) = (S

′

) :

r /∈ m

(s,o) ∧ r ∈ m

′

(s,o).

Because of the δ

∗

-equivalence lemma,

∀q ∈ Q,q

∈ Q

= q|Q

′

)

= q

′

= δ

∗

,a) = δ

∗

(q,a)|Q

= q

′

= (S

′

)

⇒ ∀s ∈ S

,o ∈ O

: m

′

(s,o) = m

′

(s,o).

Because d is a decomposition function, ∀s ∈ S

o ∈ O

: m

(s,o) = m(s, o) (property (d)).

Because r /∈ m

(s,o) = m(s, o) ∧ r ∈ m

′

(s,o) =

′

(s,o), q is not safe wrt. r.



We thus have found precise rules for decompos-

ing any HRU security model into smaller and au-

tonomous sub-models. Because the sub-models are

smaller, they generally are easier to analyze and cut

down the runtimes of heuristic safety analysis algo-

rithms. Because the sub-models are autonomous, they

can be analyzed concurrently.

The properties of the decomposition function

guarantee that the original model and its sub-models

are structurally equivalent, and that the results of sub-

model safety analysis also hold for the original model:

on the one hand, for each state that is not safe in some

sub-model, a state in the original model exists that is

not safe, too; on the other hand, for each state that is

not safe in the original model, a state in a sub-model

exists that is also not safe.

5.3 Applicability of the Decomposition

Method

In order to apply the proposed decomposition method,

systems need to have a certain property — a system’s

HRU model must be decomposable into autonomous

sub-models (Section 5.1.2). Just as our application

scenario incorporates the required system property

due to its security policy rules (separation of duty and

restricting right delegations to security domains), nu-

merous state-of-the-art systems also implement this

property by design. This section picks two prominent

examples from the business and military domain and

discusses the applicability of the proposed decompo-

sition method.

In standard business systems, the required sys-

tem property has been implemented for more than

a decade by multiclient ability — a concept applied

by a variety of standard business software, e.g. by

SAP’s business solutions with over 100.000 instal-

lations worldwide, e.g. a business software installa-

tion can be used by two or more companies in par-

allel. Multiclient ability allows to map one inde-

pendent organizational entity to one client on a soft-

ware installation, without having to install and main-

tain a separate system for each organizational en-

tity (SAP AG, 2009). Consequently, if a system sup-

ports multiple clients, the client’s data – which usu-

ally is business-critical – has to be strictly isolated

from any other client. This key requirement is usu-

ally dealt with by a sophisticated authorization policy

— the clients’ users only have rights on the clients’

objects and do not own any rights on objects of the

other clients; only users with special privileges (ad-

ministrators) own rights on all objects.

Figure 7: Business software with two clients.

Figure 7 shows the ACM of a multiclient sys-

tem with two clients. The ACM contains client-

SECRYPT 2010 - International Conference on Security and Cryptography

dependent objects (business data) for each client and

client-independent objects (customizing data) which

are system-dependent and shared by all clients. The

client’s users own the rights to read, write or execute

the client’s data; the system data can only be read or

executed by a client’s user. Consequently, this de-

sign choice is optimal for the proposed decomposition

method since an appropriate decomposition heuristics

is directly inferred from the application. As a result, a

system hosting n clients can be decomposed in n + 1

slices (rows), in n + 1 slices (columns) whereas the

client’s users and the privileged users are collected in

separate slices (see Fig.4), or in (n+1)×(n+1) slices

(checker board pattern).

Military systems commonly enforce multilevel se-

curity (MLS) policies where objects are classiﬁed into

hierarchical security levels and subjects are granted

clearances meaning that a subject is granted a clear-

ance, only if the subject is considered trustworthy

for objects up to this particular security level. The

structure of military security levels is commonly de-

scribed by the lattice model for deﬁning information

ﬂow (Denning, 1976). In order to implement these

application-oriented MLS policies, system-oriented

models based on ACMs have been extended to in-

clude security levels, clearances, and classiﬁcation

rules, e.g. the Bell and LaPadula (BLP) model (Bell

and LaPadula, 1973) which combines lattices and

state machines by deﬁning precise rules (Simple Se-

curity Rule, *-property) to control whether or not an

ACM is a correct implementation of a lattice. The

state transition function thus ensures that the ACM’s

correctness remains. As such MLS policies modeled

with the BLP model are a special case of HRU secu-

rity models (Pittelli, 1988) which abide to strict MLS

policy rules. Both the classiﬁcation of subjects and

objects to a single security level/clearance as well as

the strict MLS policy rules set the course for the pro-

posed decomposition method.

Assuming l is an MLS policy’s number of secu-

rity levels assigned to its objects and c ≤ l is the

number of clearances assigned to its subjects. The

system’s model can then be decomposed in l slices

(columns) where all sub-models have the same sub-

ject set but mutually disjoint object sets, or in c slices

(rows) where all sub-models have the same object set

but mutually disjoint subject sets (Fig. 8 with c = 3).

Hence, the subjects’ clearances respectively the ob-

jects’ security levels are then disregarded and do not

contribute to the decomposition.

In general, MLS policies allow for reclassify-

ing subjects and objects. However, depending on the

applied decomposition heuristics reclassifying a sub-

ject/object may have an impact on the sub-models’

Figure 8: Decomposition according to subject clearances.

subject or object sets. For example, if a model is de-

composed according to the subject clearances, reclas-

sifying objects according to policy rules is still state-

closed. Granting a subject a new clearance, however,

results in removing this subject from the subject set

of the old clearance and adding the subject to the new

clearance’s sub-model. Thus, state-closedness does

not hold anymore. On this account, our decomposi-

tion model supports reclassiﬁcation of either subjects

or objects. Enabling both requires (i) dynamic sub-

ject and object sets within sub-models, and (ii) the

decomposition heuristics being part of state transition

functions, which is part of our future work.

In summary, a wide variety of state-of-the-art sys-

tems can be modeled by the HRU calculus such that

the method’s requirement of autonomous sub-models

is met. Thus, the proposed decomposition method

takes a general approach and can be applied in nu-

merous application scenarios.

6 CONCLUSIONS

In this paper we described a method for analyzing

the safety properties of general, unrestricted HRU se-

curity models. The idea is to decompose a model

into autonomous sub-models and analyze their safety

properties individually. Because the sub-models are

smaller, they generally are easier to analyze, and

their smaller size signiﬁcantly reduces the runtime of

heuristic safety analysis algorithms with superlinear

runtime complexity. Because they are autonomous,

sub-models can be analyzed concurrently, allowing

to efﬁciently exploit grid and multiprocessor/multi-

core architectures. Strict properties of the decomposi-

tion function guarantee that the original model and its

sub-models are structurally equivalent, and that sub-

model safety properties map to the original model.

Finding a proper model decomposition is a chal-

EFFICIENT ALGORITHMIC SAFETY ANALYSIS OF HRU SECURITY MODELS

lenge as well as an opportunity: a challenge, because

the sub-models have to meet closeness conditions,

and an opportunity, because human knowledge is ex-

ploited to tackle the computational complexity of the

analysis.

While in general safety properties of HRU secu-

rity models are known to be undecidable, the method

allows for safety analysis in many real-world scenar-

ios. Excerpts from the security policy of a real-world

enterprise resource planning scenario and a discus-

sion of MLS models support this claim.

REFERENCES

Ammann, P. E. and Sandhu, R. S. (1991). Safety Anal-

ysis for the Extended Schematic Protection Model.

In Proc. IEEE Symposium on Security and Privacy.

IEEE Press.

Bell, D. E. and LaPadula, L. J. (1973). Secure Computer

Systems: Mathematical Foundations (Vol.I). Techni-

cal Report AD 770 768, MITRE.

Brewer, D. F. and Nash, M. J. (1989). The Chinese Wall

Security Policy. In Proc. IEEE Symposium on Security

and Privacy. IEEE Press.

Bryce, C., K¨uhnhauser, W. E., Amouroux, R., and Lop´ez,

M. (1997). CWASAR: A European Infrastructure for

Secure Electronic Commerce. Journal of Computer

Security, IOS Press.

Common3.1 (2009). Common Criteria for Information

Technology Security Evaluation, Version 3.1, Revision

Crampton, J. and Khambhammettu, H. (2008). Delegation

in Role-based Access Control. Int. Journal of Infor-

mation Security.

Denning, D. E. (1976). A Lattice Model of Secure Informa-

tion Flow. Communications of the ACM.

Efstathopoulos, P. and Kohler, E. (2008). Manageable Fine-

Grained Information Flow. In Proc. 2008 EuroSys

Conference. ACM SIGOPS.

Goguen, J. and Meseguer, J. (1982). Security Policies and

Security Models. In Proc. IEEE Symposium on Secu-

rity and Privacy. IEEE.

Halfmann, U. and K¨uhnhauser, W. E. (1999). Embedding

Security Policies Into a Distributed Computing Envi-

ronment. Operating Systems Review.

Harrison, M. A. and Ruzzo, W. L. (1978). Monotonic Pro-

tection Systems. In DeMillo, R., Dobkin, D., Jones,

A., and Lipton, R., editors, Foundations of Secure

Computation. Academic Press.

Harrison, M. A., Ruzzo, W. L., and Ullman, J. D. (1975).

On Protection in Operating Systems. Operating Sys-

tems Review, 5th Symposium on Operating Systems

Principles.

Harrison, M. A., Ruzzo, W. L., and Ullman, J. D. (1976).

Protection in Operating Systems. Communications of

the ACM.

Kleiner, E. and Newcomb, T. (2006). Using CSP to Decide

Safety Problems for Access Control Policies. Techni-

cal Report RR-06-04, Oxford University Computing

Laboratory.

Kleiner, E. and Newcomb, T. (2007). On the Decidabil-

ity of the Safety Problem for Access Control Poli-

cies. Electronic Notes in Theoretical Computer Sci-

ence (ENTCS).

Krohn, K. and Rhodes, J. (1965). Algebraic Theory of Ma-

chines. I. Prime Decomposition Theorem for Finite

Semigroups and Machines. Transactions of the Amer-

ican Mathematical Society.

Li, N., Mitchell, J. C., and Winsborough, W. H. (2005). Be-

yond Proof-of-compliance: Security Analysis in Trust

Management. JACM.

Lipton, R. and Snyder, L. (1978). On Synchronization and

Security. In DeMillo, R., Dobkin, D., Jones, A., and

Lipton, R., editors, Foundations of Secure Computa-

tion. Academic Press.

Loscocco, P. A. and Smalley, S. D. (2001). Integrating Flex-

ible Support for Security Policies into the Linux Oper-

ating System. In Cole, C., editor, Proc. 2001 USENIX

Ann. Techn. Conference.

Pittelli, P. A. (1988). The Bell-LaPadula Computer Security

Model Represented as a Special Case of the Harrison-

Ruzzo-Ullman Model. In Proc. National Computer

Security Conference. NBS/NCSC.

Sandhu, R. S. (1992). The Typed Access Matrix Model.

In Proc. IEEE Symposium on Security and Privacy.

IEEE.

Sandhu, R. S., Coyne, E. J., Feinstein, H. L., and Youman,

C. E. (1996). Role-Based Access Control Models.

IEEE Computer.

SAP AG (2009). SAP History. http://www.sap.com/.

Vimercati, S. D. C. d., Samarati, P., and Jajodia, S. (2005).

Policies, Models, and Languages for Access Con-

trol. In 4th Int. Workshop on Databases in Networkes

Information Systems, Volume 3433/2005 of LNCS.

Springer.

SECRYPT 2010 - International Conference on Security and Cryptography