AN OPTIMAL VOTING SCHEME FOR MICROANEURYSM

CANDIDATE EXTRACTORS USING SIMULATED ANNEALING

alint Antal, Istv

an L

ar and Andr

as Hajdu

University of Debrecen, Faculty of Informatics, POB 12, 4010 Debrecen, Hungary

Keywords:

Biomedical image processing, Image classiﬁcation, Pattern recognition, Medical decision-making, Statistics.

Abstract:

In this paper, we present a novel approach to improve microaneurysm candidate extraction in color fundus

images. The individual algorithms published so far can be hardly considered in an automatic screening sys-

tem. To improve further the sensitivity, speciﬁcity and image classiﬁcation rate of microaneurysm detection,

we propose an appropriate combination of individual algorithms. Thus, we investigate the detection of mi-

croaneurysms through the following phases: ﬁrst, we use different approaches to extract microaneurysm can-

didates. Then, we select candidates voted by a sufﬁcient number of the candidate extractor algorithms. The

optimal number of votes and participating algorithms are determined by a simulated annealing algorithm. Fi-

nally, we classify the candidates with a machine-learning based approach by following the current literature

recommendations. Our framework improves the positive likelihood ratio for the microaneurysms and outper-

forms both the state-of-the-art individual candidate extractors and microaneurysm detectors in these terms.

1 INTRODUCTION

Diabetic retinopathy (DR) is the most common cause

of blindness in the developed countries. Microa-

neurysms (MAs) are early signs of this disease, so the

detection of these lesions is essential in the screen-

ing process. DR can be prevented and its progression

can be slowed down if diagnosed and treated early. A

proper medical protocol (Harding et al., 2003), (Com-

mittee, 2009) has been established, but the actual

grading required for diagnostics has been performed

manually. Manual grading is slow and resource de-

manding, so several efforts have been made to estab-

lish an automatic computer-aided screening system

(Abramoff et al., 2008), (Hejlesen et al., 2004). How-

ever, the detection of microaneurysms is still an open

issue. Thus, several recent works focus on this prob-

lem, including an online challenge for MA detectors

(Niemeijer et al., 2010).

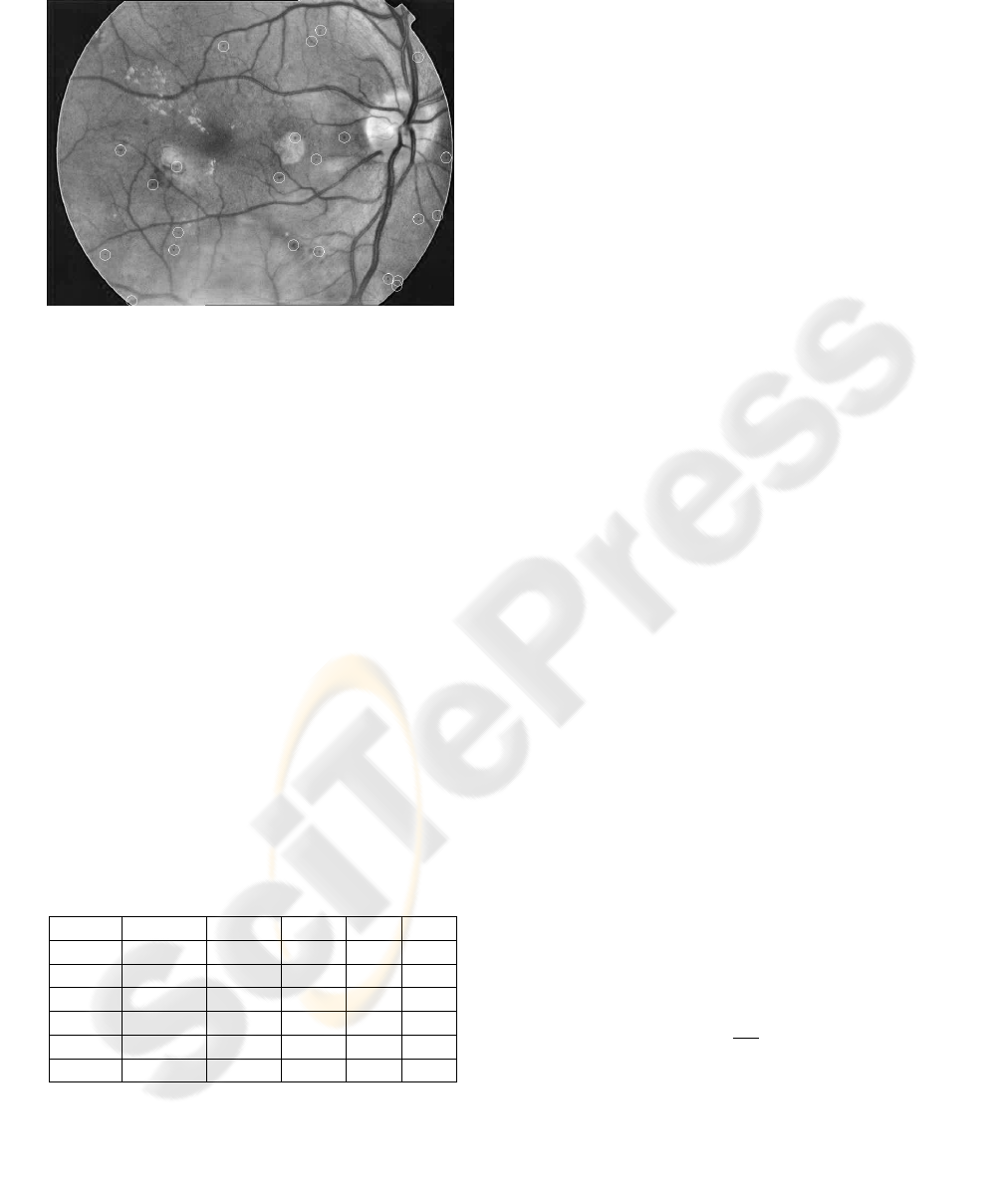
Microaneurysms appear as small circular dark

spots on the surface of the retina (see Figure 1). The

most common appearance of microaneurysms is near

thin vessels, but they cannot actually lie on the ves-

sels. In some cases, microaneurysms are hard to dis-

tinguish from parts of the vessel system. For example,

the intersections of two thick vessels or a few very

thin vessels are rather misleading for the detectors.

In this paper, we propose an ensemble-based ap-

Figure 1: Fundus image containing a microaneurysm.

proach to MA detection to suppress the errors of in-

dividual algorithms. The proposed process consists

of three main steps (see also Figure 2): ﬁrst, we ex-

tract MA candidates from fundus images after pre-

processing. For this task, we select three state-of-the-

art approaches and include a novel one, as well. In

the second phase, we combine the results provided by

the four candidate extractors and reduce the number

of candidates with a voting scheme. The number of

required votes and the set of the corresponding candi-

date extractors is determined by a simulated annealing

algorithm. We also introduce a novel machine-learn-

Antal B., L

ar I. and Hajdu A. (2010).

AN OPTIMAL VOTING SCHEME FOR MICROANEURYSM CANDIDATE EXTRACTORS USING SIMULATED ANNEALING.

In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 80-87

 SciTePress

ing based algorithm to classify the candidates. The

rest of the paper is organized as follows. In section 2

we present the MA candidate extractor algorithms to

build up an ensemble. The optimal voting scheme of

the MA extractor algorithms is described in section 3.

In section 4 the results of the ensemble-based system

are presented. Finally, some conclusions are drawn in

section 5.

Figure 2: Steps of microaneurysm detection using an en-

semble of candidate extractors.

2 MICROANEURYSM

CANDIDATE EXTRACTION

Candidate extraction is an effort to reduce the num-

ber of objects in an image for further analysis by ex-

cluding regions which do not have similar charac-

teristics to microaneurysms. Individual approaches

deﬁne their own measurement for similarity to ex-

tract MA candidates. In this section, we provide a

brief overview of currently popular candidate extrac-

tors that will be considered later on in the ensemble

system. Namely, we recall Walter et al. (Walter et al.,

2007), the Spencer-Frame method (Spencer et al.,

1996) (Frame et al., 1998) in its original form, and

a slightly modiﬁed version of (Abdelazeem, 2002). A

new approach is also involved, whose development

was partly motivated to improve the MA candidate

extraction efﬁciency of the proposed ensemble-based

system. As we will see later on, these methods sufﬁ-

ciently diverse to form a successful ensemble.

2.1 Walter et al.

This approach is proposed in (Walter et al., 2007). To

overcome the imperfections of color fundus images, a

contrast enhancement operator is applied as a prepro-

cessing step along with shade correction:

[SC ( f )] =











max

−u

min

)·( f (x)−t

min

)



∗

−t

min



+ u

min

, t ≤ µ

∗

−

max

−u

min

)·( f (x)−t

max

)



∗

−t

max



+ u

max

, t ≥ µ

∗

where {t

min

, . . . t

max

} are the intensity values of the

grayscale image, {u

min

, . . . u

max

}are the intensity val-

ues of the enhanced image, µ

∗

is the mean value of

an area opened image and r ∈ R. The parameter r

controls the level of contrast enhancement. Candidate

extraction is then accomplished by grayscale diameter

closing. That is, the method aims ﬁnd all sufﬁciently

small dark patterns on the green channel. Let

α(X) = max

x, y∈X

d (x, y)

be the diameter α of a connected set X with a distance

function d (.). Let

−

( f ) = {x|f (x) ≤t}.

Then, the grayscale diameter closing is deﬁned by the

following formula:

= inf{s ≥ f (x)|α





−

( f )



≥ α}.

Then, the candidates are the remaining objects on the

image. For an example output, see Figure 3.

Figure 3: Candidates extracted by the Walter candidate ex-

tractor.

2.2 Spencer-Frame

This approach is one of the most popular candidate

extractors, originally proposed by (Spencer et al.,

1996) and (Frame et al., 1998). The algorithm uses

shade correction as preprocessing: ﬁrst, a background

image i

is produced by applying a median ﬁlter on

the green channel of the original image i

green

. Then,

AN OPTIMAL VOTING SCHEME FOR MICROANEURYSM CANDIDATE EXTRACTORS USING SIMULATED

ANNEALING

the shade corrected image i

is established by the fol-

lowing formula:

= i

−i

green

The actual candidate extraction is accomplished by

subtracting the maximum of multiple morphological

top-hat transformations, which is deﬁned as follows:

T ( f ) = f •s − f ,

where • denotes the morphological closing. For this

step, twelve rotated structuring elements were used

with a radial resolution of 15

◦

. Then, the vascular

map is subtracted from i

to remove the largest com-

ponents form the image. As a contras enhancement

operator, a 2D Gaussian matched ﬁlter is applied on

the image. The resulting image is then binarized with

a ﬁxed threshold. Since the candidates are not a good

representation for the actual lesions, a region growing

step is also applied.

A slightly modiﬁcated version of this method is

proposed in (Niemeijer et al., 2005), (Mizutani et al.,

2009) and (Fleming et al., 2006).

For an example output, see Figure 4.

Figure 4: Candidates extracted by the Spencer-Frame can-

didate extractor.

2.3 Circular Hough-transformation

based

Based on the idea presented in (Abdelazeem, 2002),

we established an approach based on the detection

of small circular spots in the image. As a pre-

processing step, a common biomedical image cor-

rection technique, the contrast limited adaptive his-

togram equalization (CLAHE) is applied (Zuiderveld,

1994). CLAHE is realized in the following way

(Reza, 2004): ﬁrst, the image is divided into disjoint

regions. Then, for each region a histogram and a clip-

ping limit are obtained. After that, all the histograms

are redistributed according to the corresponding limit.

Finally, the cumulative distribution functions are de-

termined for grayscale mapping. The candidate ex-

traction is obtained by detecting circles on the images.

For this purpose we use circular Hough transforma-

tion (Chen and Chung, 2001). With this technique,

a set of approximately circle-shaped objects can be

obtained from the image. The radius of the circles

are limited according to the observed size of microa-

neurysms from a training set.

For an example output, see Figure 5.

Figure 5: Candidates extracted by the Circular Hough-

transformation based candidate extractor.

2.4 Lazar et al.

Besides some popular techniques mentioned so far,

we also investigate a new MA candidate extractor de-

veloped by our research group.

The green channel of the image is inverted and

smoothened with a Gaussian ﬁlter. A set of scan

lines with equidistantly sampled tangents between -

◦

and +90

◦

is ﬁxed. For each direction the inten-

sity values along the scan lines are recorded in a one

dimensional array, and the scan lines are shifted verti-

cally and horizontally to process every image pixel of

the image. On each intensity proﬁle, the heights of the

peaks, and their local maximum positions are used for

an adaptive thresholding. The resulting foreground

indices of the thresholding process are transformed

back to two dimensional coordinates, and stored in

a map that records the number of foreground pixels

of different directions corresponding to every position

of the image. The maximal value for each position

equals the number of different directions used for the

scanning process. This map is smoothened with an

averaging kernel and a hysteresis thresholding proce-

dure is applied. The resulting components are ﬁltered

based on their size. For more details, see (Lazar et al.,

2010).

SIGMAP 2010 - International Conference on Signal Processing and Multimedia Applications

For an example output, see Figure 6.

Figure 6: Candidates extracted by the Lazar candidate ex-

tractor.

2.5 Diversity of the Candidate

Extractors

It is important to use diverse candidate extractors, that

is, to reduce the number of false positives efﬁciently

and keep only those candidates on which multiple

methods agree. As the most straightforward measure,

we aim to raise the the positive likelihood ratio (num-

ber of the true positive (TP) / number of the false pos-

itive (FP)) (Johnson, 2004) using an ensemble.

The pairwise diversity of the classiﬁers can be

measured by the disagreement (D) and double fault

(DF) measure, where D, DF ∈ [0, 1]. The disagree-

ment measure sums the cases, where the extractors

disagree, but one of them is correct. The double fault

measure is the number of candidates, where both ex-

tractors agree and both are incorrect. For our aims, a

high disagreement and a low double fault measure is

the ideal. As it can be seen in Table 1, the selected

candidate extractors are quite diverse.

Table 1: Diversity of the candidate extractors.

Walter Spencer Hough Lazar D DF

x x 0.73 0.09

x x 0.77 0.04

x x 0.49 0.10

x x 0.79 0.06

x x 0.69 0.14

x x 0.74 0.12

3 AN OPTIMAL VOTING

SCHEME FOR COMBINING

THE CANDIDATE

EXTRACTORS

In this chapter, we present a new approach to select

the optimal combination of the candidate extractors.

First, for the proper comparison of the candidates ex-

tracted by the individual approaches, we must prepro-

cess them. Then, we select an optimal conﬁguration

for the voting scheme by a simulated annealing algo-

rithm. Finally, the voting is executed using this con-

ﬁguration. Later on, we present some properties of

this optimal voting scheme.

3.1 Preprocessing the Candidates

Before letting the individual candidate extractor al-

gorithms vote, we must ensure that there are no can-

didates too close to each other within the output of

an individual algorithm. This issue is addressed by

merging them. It is also important to remove any can-

didates falling on the vessel system. For this purpose,

we have detected the vascular system with the algo-

rithm proposed in (Staal et al., 2004) and removed the

candidates falling on vessels.

3.2 Selecting an Optimal Voting

Conﬁguration using Simulated

Annealing

The proposed framework aims to ﬁnd an optimal vot-

ing scheme for candidate extractors. This voting

scheme determines a subset of the candidate extrac-

tors and the number of required votes. Since this

problem induces a large search space, we use simu-

lated annealing to ﬁnd an optimal solution.

Simulated annealing (Kirkpatrick et al., 1983) is

a widely used global optimization method. This ap-

proach is inspired by the annealing in metallurgy. It

is effective for large search space problems by us-

ing random sampling to avoid stuck in a local mini-

mum. For the optimization, we use the following en-

ergy function to be minimized:

E = −

T P

where TP stands for the number of the true, while FP

stands for that of the false positive candidates, respec-

tively.

To minimize the target energy E by simulated

annealing, each element of the search space S con-

sists of the results sets of a set of candidate extrac-

AN OPTIMAL VOTING SCHEME FOR MICROANEURYSM CANDIDATE EXTRACTORS USING SIMULATED

ANNEALING

tors {ce

, . . . ce

} and a required number of votes v

(1 ≤ v ≤L). Each combination occurs in S only once.

The proposed simulated annealing algorithm op-

erates through the following steps:

1. Let T be an initial temperature, T

min

a minimal

temperature, 0 ≤ q ≤ 1, q ∈ R the temperature

change, S = P (({R

}, v)) the search space, where

is the result of the candidate extractor ce, v

is the number of required votes and P (X) is the

power set of X.

2. Choose x ∈ S randomly and let e = E (x), S = S −

{x}.

3. Choose x

∈ S randomly and let e

= E (x

), S =

S −{x

4. If T < T

min

or S =

0, then stop.

5. If e

< e, then x = x

, e = e

and T = T ·q . Go to

step 4.

6. Choose a random number r ∈ R. If

accept (e, e

, T, r) = true, then x = x

, e = e

where

accept (e, e

, T, r) =

(

true, i f exp



e−e



> r,

f alse, otherwise.

7. Let T = T ·q. Go to step 4.

Currently, we consider four candidate extractors

(that is, L = 4 in the algorithm above), but with the

use of simulated annealing it can be easily extended

to more methods in the future.

3.3 Voting on the Candidates

Each individual candidate extractor algorithm pro-

duces an initial set of microaneurysm candidates.

Then, we establish a set of ﬁnal candidates, where

these candidates are voted by at least n ≥ 2 candidate

extractors. The voting procedure has the following

steps:

1. For each candidate c provided by one of the algo-

rithms, check, whether there is another candidate

detected by another algorithm within a distance

r ∈ R from c.

2. Let sum be the number of candidates satisfying

the above proximity criterion and remove all these

candidates from their respective initial sets.

3. If sum ≥n, then add the centroid of the candidates

found by step 2 to the ﬁnal set.

4. Repeat the procedure until all the initial sets be-

come empty.

The result of the voting for the previously shown

example is presented in Figure 7.

Figure 7: Result of the voting.

3.4 Properties of the Optimal Voting

Scheme

Property 1. The optimal voting scheme selects a sub-

set of the candidate extractors.

That is, it is not mandatory that all available can-

didate extractors participate in the voting.

Property 2. An individually less accurate algorithm

can be still useful in an ensemble.

The optimal voting scheme can make use of some

individually less accurate algorithm in certain situa-

tions. The results of a simple majority voting with a

ﬁxed conﬁguration can be less accurate with a weaker

participant.

Property 3. The use of simulated annealing makes it

possible to include a large number of candidate ex-

tractors.

The number of combinations using n candidate

extractors is 2

−1 with excluding the empty com-

bination. For a large search space, an approximately

optimal solution can also be obtained with simulated

annealing by setting a proper annealing schedule in

less computational time.

Property 4. The optimal voting scheme determines

the number of required votes from the candidate ex-

tractors.

Thus, the system is more ﬂexible when changing

energy functions.

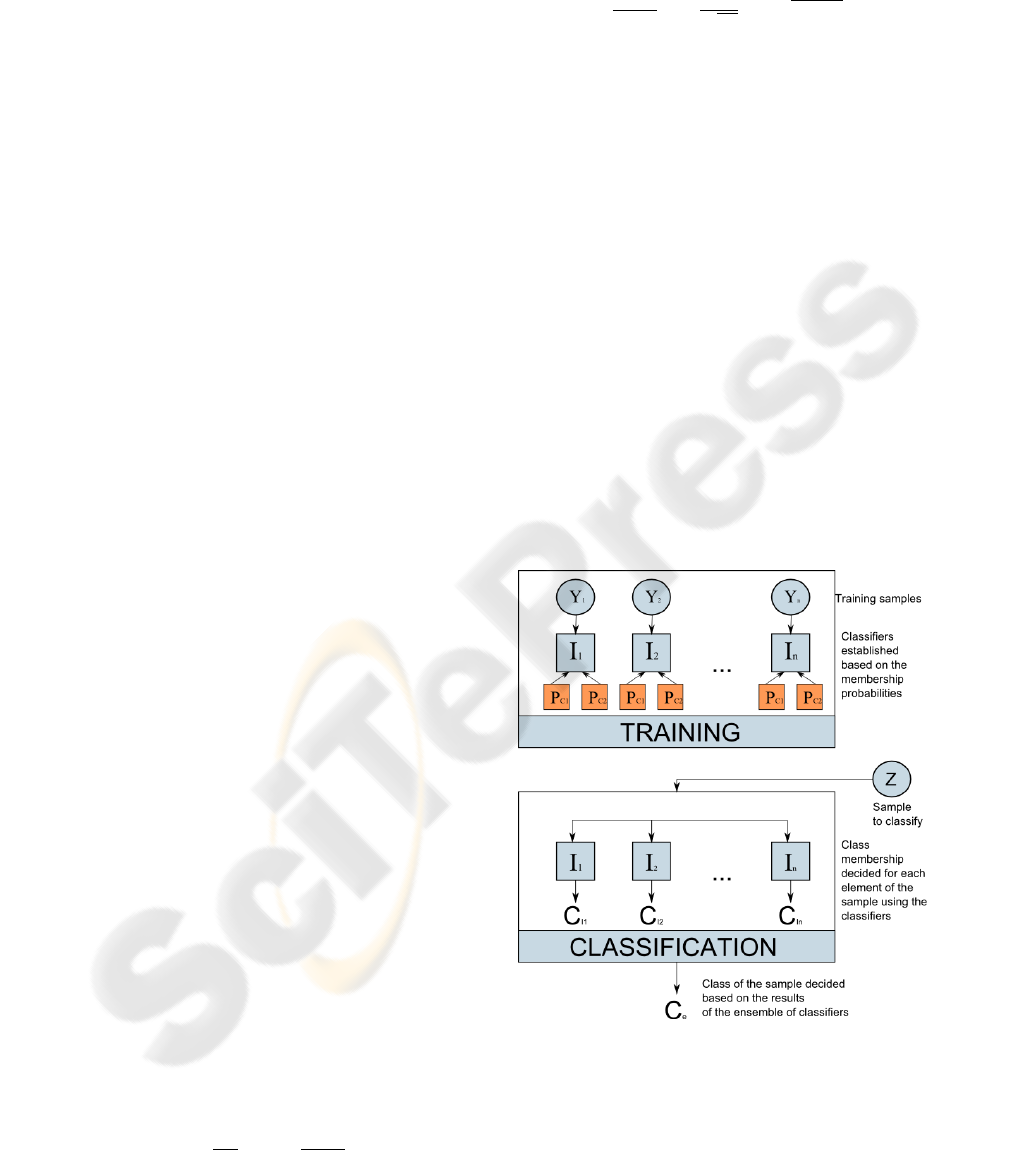
3.5 Candidate Classiﬁcation

To improve the TP / FP ratio we use a consequent

classiﬁcation step, which is based on certain unique

features of microaneurysms. We use a new approach

SIGMAP 2010 - International Conference on Signal Processing and Multimedia Applications

to perform this step, instead of other literature rec-

ommendations. The reason to introduce a new clas-

siﬁer is that the existing methods use objects and not

single pixels representations to extract features, while

our ensemble-based system provides the latter.

Candidates are classiﬁed as actual MAs or non-

MAs in two steps. First, we train our approach with

several ﬁxed size (e.g. 21 ×21 pixels) subimages for

both microaneurysm and random non-microaneurysm

examples. Then, for each pixel of the examples, we

establish a kernel density estimator for both classes.

After the training step, we can classify new instances.

We establish a new instance by producing a subim-

age of the candidate pixel and its neighborhood with

the same size as the training step. The classiﬁcation

procedure is then the following: for each pixel of the

instance we compare the probability provided by the

kernel density estimators for both classes. Then, the

candidate is considered as a microaneurysm if more

comparisons conﬁrm that this is a positive example.

For the stages of our classiﬁer, see Figure 8.

Formally, the classiﬁer can be described in the fol-

lowing way:

Let

E = {I

, I

, . . . I

}

an ensemble of classiﬁers, where

I : x →C, x ∈ D ⊂ R

and C is a class. In our case,

D = {0, 1, . . . 255}

and

C ∈ {C

, C

Non−MA

where C

and C

Non−MA

denotes the class of Microa-

neurysms and Non-Microaneurysms, respectively.

Let

T = {

, c

, . . .

, c

}

be the training dataset, where

= {x

, x

, . . . x

, },

∈ D, i = 1 . . . n, j = 1 . . . m

is a sample and c

∈C is the corresponding class. We

establish n classiﬁer for each element of the samples,

where the I

, k = 1, . . . n is trained using

= {x

, . . . , x

Let f

(y) is the probability density function of Y

. We

establish a kernel density estimator

(y) to approxi-

mate f

(y):

(y) =

∑

i=1



y −y



where y ∈ Y

, h is a smoothing parameter and K is a

Gaussian kernel function (with µ = 0, σ = 1):



y −y



√

2π

exp

−

(

y−y

)

We establish kernel density estimators for each class,

from which the membership probability function P :

D → R can be derived. Thus, we deﬁne I

with the

following formula:

(x) = argmax

P(x|C).

The ﬁnal classiﬁcation for the sample Z by the ensem-

ble O is decided using the following formula:

O(Z) = {C

∑

i=1

) = max

∑

i=1

)},

k, l = 1, . . . , m,

where

) =

(

1, I

= C

0, otherwise.

In our case, the samples are subimages, while the

kernel density estimation are based on the pixel inten-

sities.

Figure 8: Stages of classiﬁcation.

In Figure 9 we can see the effect of this classiﬁca-

tion method applied to the previously shown example

output. We can see how a large number of FPs has

been removed.

AN OPTIMAL VOTING SCHEME FOR MICROANEURYSM CANDIDATE EXTRACTORS USING SIMULATED

ANNEALING

Committee, U. N. S. (2009). National Screen-

ing Programme for Diabetic Retinopathy.

http://www.retinalscreening.nhs.uk/.

Fleming, A. D., Philip, S., and Goatman, K. A. (2006). Au-

tomated microaneurysm detection using local contrast

normalization and local vessel detection. IEEE Trans-

actions on Medical Imaging, 25(9):1223–1232.

Frame, A. J., Undrill, P. E., Cree, M. J., Olson, J. A.,

McHardy, K. C., Sharp, P. F., and Forrester, J. (May

1998). A comparison of computer based classiﬁcation

methods applied to the detection of microaneurysms

in ophthalmic ﬂuorescein angiograms. Computers in

Biology and Medicine, 28:225238.

Harding, S., Greenwood, R., Aldington, S., Gibson, J.,

Owens, D., Taylor, R., Kohner, E., Scanlon, P.,

and Leese, G. (December 2003). Grading and dis-

ease management in national screening for diabetic

retinopathy in england and wales. Diabetic Medicine,

20:965971.

Hejlesen, O., Ege, B., Englemeier, K.-H., Aldington, S.,

McCanna, L., and Bek, T. (2004). Tosca-imaging de-

veloping internet based image processing software for

screening and diagnosis of diabetic retinopathy. MED-

INFO 2004, pages 222–226.

Johnson, N. P. (2004). Advantages to transforming the re-

ceiver operating characteristic (roc) curve into like-

lihood ratio co-ordinates. Stastics in Medicine,

23:22572266.

Kirkpatrick, S., Gelatt, C. D., and Vecchi, M. P. (May 13,

1983). Optimization by simulated annealing. Science,

220:671–680.

Lazar, I., Hajdu, A., and Quareshi, R. J. (2010). Retinal mi-

croaneurysm detection based on intensity proﬁle anal-

ysis. 8th International Conference on Applied Infor-

matics.

Mizutani, A., Muramatsua, C., Hatanakab, Y., Suemoria,

S., Haraa, T., and Fujita, H. (2009). Automated

microaneurysm detection method based on double-

ring ﬁlter in retinal fundus images. Medical Imag-

ing 2009: Computer-Aided Diagnosis, Proceedings of

SPIE, 7260, 7260:1N1 – 1N8.

Niemeijer, M., Staal, J., Abramoff, M. D., Suttorp-Schulten,

M. A., and van Ginneken, B. (May 2005). Automatic

detection of red lesions in digital color fundus pho-

tographs. IEEE Transactions on Medical Imaging,

24:584–592.

Niemeijer, M., van Ginneken, B., Cree, M., Mizutani,

A., Quellec, G., Sanchez, C., Zhang, B., Hornero,

R., Lamard, M., Muramatsu, C., Wu, X., Cazuguel,

G., You, J., Mayo, A., Li, Q., Hatanaka, Y., Coch-

ener, B., Roux, C., Karray, F., Garcia, M., Fujita, H.,

and Abramoff, M. (2010). Retinopathy online chal-

lenge: Automatic detection of microaneurysms in dig-

ital color fundus photographs. IEEE Transactions on

Medical Imaging, 29(1):185–195.

Reza, A. M. (2004). Realization of the contrast limited

adaptive histogram equalization (clahe) for real-time

image enhancement. The Journal of VLSI Signal Pro-

cessing, 38:35–44.

Spencer, T., Olson, J. A., McHardy, K. C., Sharp, P. F.,

and Forrester, J. V. (May 1996). An image-processing

strategy for the segmentation and quantiﬁcation of mi-

croaneurysms in ﬂuorescein angiograms of the oc-

ular fundus. Computers and Biomedical Research,

29:284302.

Staal, J., Abramoff, M. D., Niemeijer, M., Viergever, M. A.,

and van Ginneken, B. (2004). Ridge-based vessel seg-

mentation in color images of the retina. IEEE Trans-

actions on Medical Imaging, 23:501 – 509.

Walter, T., Massin, P., Arginay, A., Ordonez, R., Jeulin, C.,

and Klein, J. C. (2007). Automatic detection of mi-

croaneurysms in color fundus images. Medical Image

Analysis, 11:555–566.

Zuiderveld, K. (1994). Contrast limited adaptive histogram

equalization. Graphics gems, IV:474–485.

AN OPTIMAL VOTING SCHEME FOR MICROANEURYSM CANDIDATE EXTRACTORS USING SIMULATED

ANNEALING