MOBILITY AND SECURITY MODELS FOR WIRELESS SENSOR
NETWORKS USING VORONOI TESSELLATIONS
Manel Abdelkader, Mohamed Hamdi and Noureddine Boudriga
Communication Networks and Security Research Lab., University of Carthage, Carthage, Tunisia
Keywords:
Wireless sensor networks, Collaborative computing, Voronoi tessellation, Mobility models.
Abstract:
Recent advances in integrated electronic devices motivated the use of wireless sensor networks in many appli-
cations including target surveillance and tracking. A number of sensor nodes are scattered within a sensitive
region to detect the presence of intruders and forward subsequent events to the analysis center(s). Obviously,
the sensor deployment should guarantee and optimal event detection rate. This paper proposes a high-level
Voronoi-based technique to assess the area coverage based on information available locally for each sensor
node. We show that the proposed technique can be used to implement a coverage-preserving mobility process
to enhance the initial sensor deployment. We also highlight other potential applications of our approach.
1 INTRODUCTION
Wireless Sensor Networks (WSNs) are among the
technologies that will probably shape the first decades
of the twenty first century. These networks are mainly
cost-effective, easy to deploy, and multi-purpose. In
fact, WSNs have been used in various contexts in-
cluding mobile target detection, healthcare, water re-
source monitoring, and virtual reality. However, they
are also characterized by severe memory, CPU, and
(most importantly) energy limitations that hardens
their deployment in environments where voluminous
data should be processed and high-speed networks are
to be used to transmit these data. For instance, exist-
ing WSNs devised for military surveillance often pro-
vide coarse data about the hostile target(s) moving in
the battlefield. This constraint, mainly fixed by the
sensor node cost, considerably affects the efficiency
of the WSN.
The major WSN design issue that should be con-
sidered in target tracking applications is area cover-
age. This is because a sensor node detects the pres-
ence of hostile targets only if they are within its sens-
ing range. Therefore, the WSN detection perfor-
mance depends on how well the sensors observe the
physical space. In (Gui and Mohapatra, 2004), cov-
erage degree has been thought of as a measure of the
WSN quality of surveillance. A metric, called Aver-
age Linear Uncovered Length (ALUL), has been de-
veloped to estimate the average distance a mobile tar-
get can make before being detected by the sensor net-
work. Therefore, the ALUL can be used to assess the
detection efficiency of the WSN. However, the ma-
jor shortcoming of this approach is its heavy compu-
tational load making it non-conforming with the se-
vere processing and energy limitations characterizing
WSNs. This complexity is exacerbated when the met-
ric is extended to k-coverage assessment, where k > 1.
This paper proposes a coverage assessment ap-
proach amenable to implement advanced target track-
ing functionalities using a hybrid framework com-
posed of a large number of resource-impoverished
sensor nodes and a small number of powerful sen-
sor nodes. We rely on a WSN framework, called
WHOMoVeS (Wireless Hybrid Optimal Mobile Ve-
hicle Sensing), which has been introduced in (Obai-
dat, 2008) for military surveillance. To address this
issue, we build a higher-order Voronoi diagram of
the monitored region for an efficient estimation of
the local coverage degree. A collaborative comput-
ing framework is set up to fulfill this task. Through-
out the paper, we give a general overview of the WSN
tasks that may take benefit of the proposed coverage
assessment method (i.e., mobility modeling, activity
scheduling). To the best of our knowledge, this is the
first time higher-order Voronoi tessellations are used
in the WSN context, even though simple Voronoi di-
agrams have already been investigated (Wang et al.,
2007; Stojmenovic et al., 2003; Vieira et al., 2003).
The major contributions of the paper are listed in
the following:
• The proposed cooperative coverage assessment
approach considerably reduces the computational
104
Abdelkader M., Hamdi M. and Boudriga N. (2010).
MOBILITY AND SECURITY MODELS FOR WIRELESS SENSOR NETWORKS USING VORONOI TESSELLATIONS.
In Proceedings of the International Conference on Data Communication Networking and Optical Communication Systems, pages 104-113
DOI: 10.5220/0002989501040113
Copyright
c
 SciTePress

complexity with regard to existing methods
• Besides coverage optimization, higher-order
Voronoi tessellations can be useful for perform-
ing multiple tasks including activity scheduling or
distributed cryptographic protocols
• Local coverage information, gathered using the
Voronoi diagram, can be used to implementcover-
age preserving mobility models. A simple model
is presented in this paper to show that our idea
considerably enhances the WSN target detection
performance
The rest of the paper is structured as follows. Sec-
tion 2 gives an overview on the WHOMoVeS and
ALUL concepts, which are of utmost importance in
our work. A mathematical introduction to Voronoi
tessellations is presented in Section 2. Section 3
highlights the potential applications of k-Voronoi di-
agrams in WSNs. We particularly show in Section 4
how this tessellation is used to develop a coverage-
preserving mobility model. The higher-order Voronoi
diagram is also shown to be helpful in defining ac-
tivity scheduling strategies and security schemes. Fi-
nally, Section 8 concludes the paper.
2 RELATED WORK
This section first reviews a WSN framework that has
been introduced by the authors in (Obaidat, 2008).
Then, we give the basic definitions related to the
ALUL metric.
2.1 WHoMoVeS: a Framework for
Military Target Tracking
At this stage, the reader may wonder about the choice
of WHOMoVeS as a WSN framework. In fact, the
main reason motivating this choice is that WHO-
MoVeS builds upon a heterogeneous multi-layer ar-
chitecture enabling the support of advanced (image
and electromagnetic-based) target tracking function-
alities, which is very important for military applica-
tions. More accurately, Hamdi et al. (Obaidat, 2008)
present WHOMoVeS as an heterogeneous sensor net-
work composed of two layers:
• The core layer, consisting of sensor nodes
equipped with powerful data gathering and trans-
mission capabilities
• The sensing layer consisting of miniature devices
whose role is restricted to the detection of hostile
presence
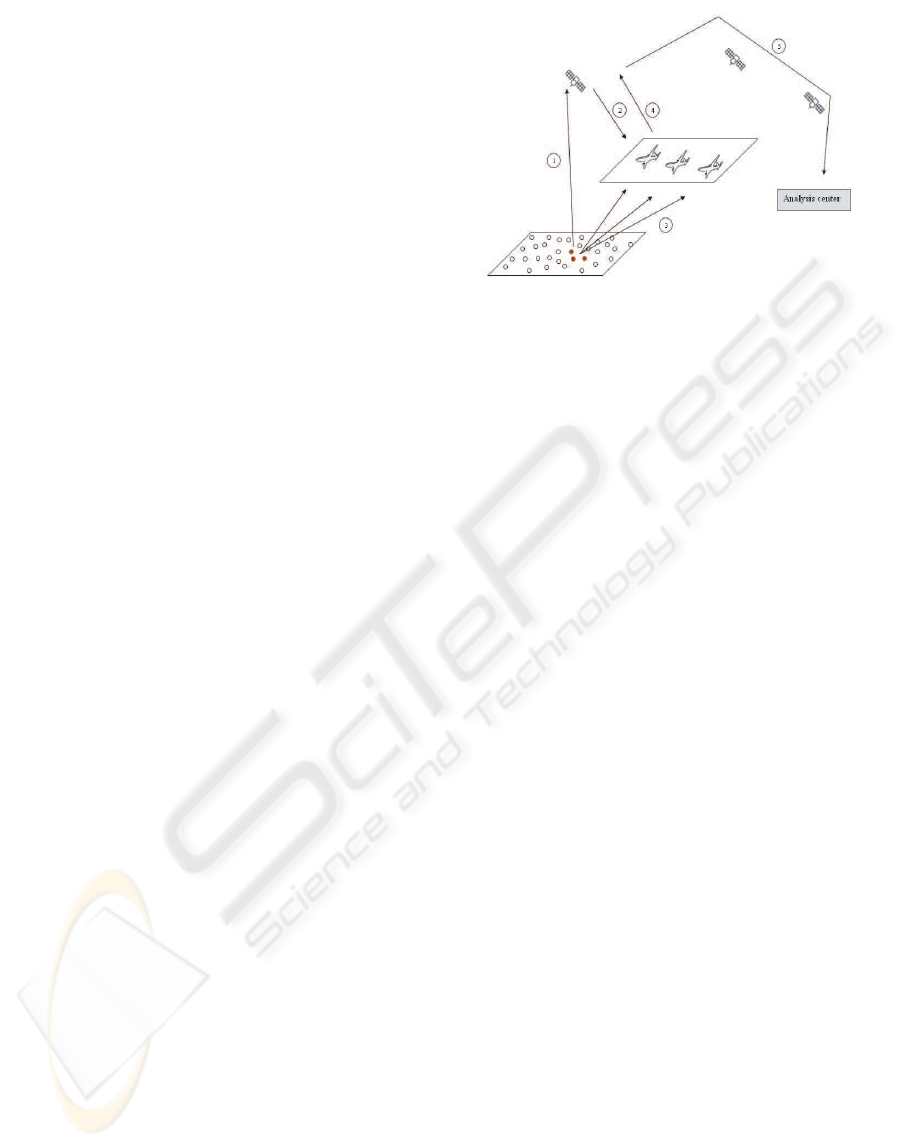
Figure 1: Architecture of the proposed satellite-based com-
munication backbone.
Accurate tracking and long network lifetime are
achieved through a strong cooperation between those
layers.
According to this reasoning, the process of acquir-
ing and analyzing data related to mobile targets in the
battlefield includes five steps as illustrated in Figure
1. These steps are briefly described in the following:
1. Ground sensors detect the presence of a hostile
target in the monitoredfield and store the events in
memory. The satellite periodically contacts sen-
sor nodes to download updates about target pres-
ence.
2. The satellite contacts the Uninhabited Aerial Ve-
hicles (UAVs) to acquire image data about the
scene where the intrusion has been detected.
3. The UAVs gather image data through the embed-
ded imaging sensors.
4. The UAVs establish connections with the satel-
lite communication backbone in order to transmit
high-quality multimedia data about the battlefield.
5. Images related to multiple intrusion events are for-
warded through the broadband satellite backbone
to the analysis center where advanced tracking
functionalities are carried out.
2.2 The ALUL Metric
The Average Linear Uncovered Length (ALUL),
introduced in (Gui and Mohapatra, 2004), gives an
approximation of the distance that can be made by a
target before being detected by the sensor network.
The undetected path length of a target travel-
ing from location (x,y) with direction θ is given by
the the Linear Uncovered Length (LUL), denoted by
L ((x, y),θ). The average of target paths before detec-
tion at location x and over all directions is the Average
MOBILITY AND SECURITY MODELS FOR WIRELESS SENSOR NETWORKS USING VORONOI
TESSELLATIONS
105

Linear Uncovered Length (ALUL(x,y)) which means
the average distance can be traveled by a target at the
location (x,y) without be detected. Obviously, if (x,y)
is within the coverage of at least one sensor node then
ALUL(x,y) equals 0. More generally, ALUL(x) is cal-
culated as follows:
ALUL(x,y) ≡
(
0 : (x,y) is covered
R
2π
0
L ((x,y),θ)dθ
2π
: otherwise
(1)
The ALUL in an area A, denoted by ALUL(A) is
the mean uncovered distance that can be traveled by
a target without being detected by any of the nodes
deployed in the region of interest. The expression of
ALUL(A) is given by:
ALUL(A) ≡
R
(x,y)∈A
ALUL(x,y)dxdy
k A k
,
(2)
where k A k is the area of A.
3 HIGHER-ORDER VORONOI
TESSELLATIONS AND WSN
COVERAGE
The objective of this section is to provide a tool for
accurately gauging the coverage degree of the moni-
tored zone. To this purpose, we rely on higher-order
Voronoi diagrams to determine the sub-regions that
do not satisfy the k-coverage requirement. First, we
give a mathematical representation for higher order
Voronoi tessellation, which is a set of Voronoi cells.
Then, a parallel calculation framework allowing an
efficient computation of this tessellation is provided.
3.1 Mathematical Modeling of
Higher-order Voronoi Diagrams
We start by the definition of the mathematical model
related to sensor nodes distribution. We identify the
groups of the k-nearest neighbors using the higher or-
der Voronoi model.
Let M be a metric space; δ : M × M → R de-
noting the Euclidean distance on M. We denote by
R = {p
i
,1 ≤ i ≤ N} ⊆ M , a set of N sensor nodes
having their coordinates in M.
The Voronoi diagram associated to R is the unique
subdivision defined in M such that every part of the
subdivision contains the nearest neighbors defined in
M for p
i
,1 ≤ i ≤ N, in R. Every subdivision part is
named a Voronoi Cell related to p
i
,1 ≤ i ≤ N, and is
determined using the following process.
For every p
i
, p
j
∈ R , we denote by H(p
i
, p
j
) the
half plane containing p
i
:
H(p
i
, p
j
) =

x ∈ M/δ(p
i
,x) < δ(p
j
,x)

. (3)
It can be noticed that H(p
i
, p
j
) is the half plane
delimited by the bisector of line segment [p
i
, p
j
] and
including p
i
.
The Voronoi cell related to p
i
is generated by the
definition of the common area between all half-planes
defined aboveand containing p
i
. Therefore, a Voronoi
cell related to p
i
is expressed by:
V
R
(p
i
) =
\
p
j
∈R\{p
i
}
H(p
i,
p
j
). (4)
In our work, we are rather interested in partition-
ing M into isotopic cells according to k-nearest neigh-
bors for a given distribution of p
i
, p
j
∈ R. Start-
ing from a given sensor distribution, we search the
set P
(k)
i
= {p
i1
,..., p
ik
} containing the nearest sen-
sor neighbors. Such groups can be obtained using the
higher order-k Voronoi Diagram. The latter allows
defining subsets of M containing the nearest elements
to P
(k)
i
. This can be performedby finding the elements
which are closer to the most distant neighboring of
P
(k)
i
than any other p
j
/∈ P
(k)
i
. In other terms, it can be
written that:
V(P
(k)
i
) =
(
x|∀p
j
∈ P\ P
(k)
i
, max
p
it
∈P
(k)
i
(δ(x, p
it
) ≤ δ(x, p
j
)
)
.
(5)
P
(k)
i
is called the generator of this Voronoi cell
V(P
(k)
i
). As for the order-1 voronoi cells, an order-k
cell is constructed using bisectors between its genera-
tors and the remaining of the metric space.
V(P
(k)
i
) =
T
p
j
∈R\P
(k)
i
[H(p
i1
, p
j
) ∩ ... ∩ H(p
ik
, p
j
)].
3.2 k-Voronoi Diagram Construction
In this section, we define the k-Voronoi diagram con-
struction model. The latter is based on the cooper-
ation of R elements. In the following, we present
the construction k-Voronoi diagram construction al-
gorithm.
Assumptions:
• Every iteration is related to an initial distribution
of R’s elements on M.
• Every sensor node present in the sensor layer
knows his “direct” neighbors (defined in his de-
tection coverage or given by a core sensor).
• The presented algorithm is based on the parallel
PRAM algorithm. In this algorithm, we present
the parallel construction of k-Voronoi diagram.
DCNET 2010 - International Conference on Data Communication Networking
106

Algorithm 1: PRAM Algorithm.
Input:A set R of planar sensors, voronoi of order k−
1.
Output: the Voronoi diagram of order k.
1. Subdivide each region r
k−1
i
induced by P
(k−1)
t
⊂ R
into subregions according to V
1
(RP
(k−1)
t
)
2. Merge equivalent new subregions relevant to
neighboring r
k−1
i
.
3. Delete old edges and save the new vertices and
edges of each r
k
i
′
.
4 A K-VORONOI-BASED
MOBILITY MODEL
In this section, we show how higher-order Voronoi
diagrams can be used to implement sensor mobility
modeling. We consider two mobility models:
• The first is an advanced model in which sensor
nodes move toward regions where the hostile tar-
get is supposed to be
• The second relies on estimating the uncovered
zones within a Voronoi cell and moving sensor
nodes toward the ’most uncovered region’
4.1 Advanced Mobility Model
Obviously, the first model is more energy-consuming
since it encompasses the prediction of the target po-
sition. Therefore, we suppose that the second model
can be used when energy resources become scarce.
The performance of both models will be assessed in
the following sections.
Moreover, the prediction function is tightly related
to the coverage of the studied zone. In fact, the greater
is the number of target detection signals, the better is
the prediction precision. In the following, we distin-
guish both cases of a target crossing a k−covered and
a non k−covered zone.
For a Target Crossing a k−covered Zone
The mobility algorithm is triggered upon the detec-
tion of a target presence. Every ground sensor sends
his detection signal to the relevant intermediate sen-
sor. The latter collects all detection signals, verifies
their integrity and defines the zones that might include
the target. The set of defined zones are classified ac-
cording to the probability of presence of the target.
This probability reaches his maximum when a zone
is k−covered. The mobility algorithm is defined as
follows:
1. The nearest k sensors s
i
, 1 ≤ i ≤ k, send their de-
tection signals to their intermediate sensors.
2. In the case where detection signals are sent to dif-
ferent intermediate sensors, the latters coordinate
to gather all signals at the IS with the highest num-
ber of detection signals.
3. IS verifies the k−security of the received signals
and constructs the zone of presence of the target
z
t
.
(a) Let’s d
i
be the detection signal of the sen-
sor s
i
. d
i
= (r
ti
,α
ti
,θ
ti
,s
i
) where r
ti
=
p
(x
s
i
− x
t
i
)
2
+ (y
s
i
− y
t
i
)
2
, α
ti
= tan
−1
(
y
s
i
−y
t
i
x
s
i
−x
t
i
),
θ
ti
is the detection instant. For every s
i
, IS
computes the detection zone z
i
such that z
i
=
R
α
ti
+δα
α
ti
−δα
R
r
ti
+δr
r
ti
−δr
dαdr where δα, δr are the es-
timated detection error. The total target pres-
ence zone is resulted from the intersection be-
tween all the elementary detection zones. Thus,
z
t
= ∩
1≤i≤k
z
i
4. IS defines ∆Z as the zone surrounding z
t
and that
a target can not go beyond in the next mobility
step. IS computes the intersection between Z
T
=
z
t
+ ∆Z and the k−Voronoi diagram: ∪
p
(k)
i
∈S
∗
k
(Z
T
∩
V(P
(k)
i
)) = ∪
i
δV
(k)
i
, where δV
(k)
i
⊆ V
i
(P
(k)
i
) such
that V
i
(P
(k)
i
) is the Voronoi cell of the k−sensors
with index i.
5. To guarantee k−coverage in Z
T
, each δV
(k)
i
should be k−covered which means that δV
(k)
i
⊂
∩ Γ
1≤ j≤k
(s
j
,R
s
).
6. A mobility instruction is defined by (r
i
,α
i
) where
r
i
≥ d(s
i
, p) such that ∃ p, ∀q ∈ δV
(k)
i
, d(s
i
, p) ≥
d(s
i
,q). and α
i
= argmax
d
xs
i
y where x,y ∈ v
i
and
v
i
is the set of the vertices of δV
i
.
For a Target Crossing a non k−covered Zone
In this case, only k
′
signed detection signals are re-
trieved by the intermediate sensors. IS proceeds at
the construction of the probable zone of presence of
the target as presented previously. In the same time, in
order to refine the target presence zone, IS starts the
recovery of the remaining (k − k
′
) required signals.
For this purpose, IS proceeds as follows:
1. let’s z
i
be a probable zone of presence of a target,
p
i
be the probability of presence of a target where
p
i
= k
i
/k such that k
i
is the number of the verified
MOBILITY AND SECURITY MODELS FOR WIRELESS SENSOR NETWORKS USING VORONOI
TESSELLATIONS
107

detection signals received by the IS and k is the
minimum required number of signals.
2. IS defines the nearest k sensors to each part of
the zone z
i
. Thus, IS defines the intersection be-
tween z
i
and the k−Voronoi diagram and deduces
∪
i
δV
(k)
i
.
3. For each δV
(k)
i
, IS ascertain the sets of the nearest
ksensors, verifies which sensors k
i
”, 0 ≤ k
i
” ≤ k
′
,
have sent detection signals. IS classifies δV
(k)
i
ac-
cording to the value of k
i
”. The greater k
i
” is, the
most important is the probability of presence of
the target in δV
(k)
i
. A small value of k
j
” induces
that the target is going in or out δV
(k)
j
.
4. For each δV
(k)
i
, IS guides the (k− k”) nearest sen-
sors to move towards δV
(k)
i
. For that, he sends
them the mobility instruction including the proba-
bility of presence of a target A mobility instruc-
tion is defined as.(r
i
,α
i
, p
i
) where r
i
≥ d(s
i
, p)
such that ∃ p, ∀q ∈ δV
(k)
i
, d(s
i
, p) ≥ d(s
i
,q). and
α
i
= argmax
d
xs
i
y where x, y ∈ v
i
and v
i
is the set of
the vertices of δV
i
, p
i
= k”/k is the probability of
presence of the target in δV
(k)
i
.
To enhance coverage while keeping more mobility
freedom, we suggest a group mobility model in which
ground sensors move in groups such that they pre-
serve a k−coverage. For this purpose, for each mo-
bility step, sensors define randomly groups of k mem-
bers for each, the latters are not required to be the
nearest neighbors. Each group defines randomly a
head which chooses the first mobility step. The
remaining members of the group take into account
this choice to determine, in turn, their next mobil-
ity step. By this manner, each sensor’s mobility step
depends on his integrating group. Further, a sensor
may move from one group to another in each mobil-
ity step. This model enables the definition of overlap-
ping k−Voronoi groups which increases the guarantee
to have a k−coverage.
4.2 Simplified Mobility Model
We propose a mobility model which is only based on
the Voronoi diagram. The following proposition gives
a condition for a Voronoi cell to be partly uncovered.
Proposition 4.1. Let S be a set of sensor node posi-
tions and s
i
in S be a sensor node. If there exists n
j
in
N(s
i
,V(S)) such that d(s
i
,n
j
) > 2R
s
i
then V(s
i
) is not
fully covered.
Proof. We suppose that d(s
i
,n
j
) > 2R
s
i
. Let [v
p
,v
q
]
be the Voronoi edge defined by n
j
and s
i
. The inter-
section of [v
p
,v
q
] and [s
i
,n
j
] is denoted by P. The
properties of the Voronoi diagram give that:
d(s
i
,P) = d(n
j
,P) =
d(s
i
,n
j
)
2
. (6)
Since d(s
i
,n
j
) > 2R
s
i
, we deduce from Equation 6
d(s
i
,P) > R
s
i
.
Consider the point Q ∈ [s
i
,P] such that d(s
i
,Q) =
R
s
i
. We can conclude that for every T ∈ [P, Q], T ∈
V(s
i
) and T /∈ Γ(s
i
,R
s
i
) (because d(s
i
,T) > R
s
i
). This
means that V(s
i
) is not totally covered.
This result can serve to implement a mobility al-
gorithm where a sensor node looks for one or more
neighbors that are at least 2R
s
i
-distant from it. If
such nodes exist, the sensor node moves toward the
most distant neighbor, denoted by n
f
, with a distance
d(s
i
,n
f
)−2R
s
i
2
.
Figure 2 illustrates this reasoning. In fact, we no-
tice that the disc centered in s
1
and having a radius
equal to R
s
i
does not cover the Voronoi cell generated
by s
1
. Hence, s
1
will move toward s
3
with a distance
d(Q,P).
Figure 2: Simplified mobility model.
The following corollaries extend this strategy to
the case where the monitored region is required to be
k-covered. For the sake of parsimony, we do not pro-
vide proofs for these corollaries in this paper.
Corollary 4.2. For s
i
in S, if |N(s
i
,V(S))| < k, where
|.| denotes set cardinality, then V(s
i
) is not k-covered.
Before giving the second corollary, we define, for
a sensor node s
i
in S, the set X(s
i
,V(S)) of intersec-
tion points expressed as follows:
X(s
i
,V(S)) =
^
V(S\ {s
i
})
\
Γ(s
i
,R
s
i
), (7)
where
e
P, for P ∈ R
2
denotes the boundary of P.
Informally speaking, X(s
i
,V(S)) denotes the in-
tersection of edges of the Voronoi diagramV(S\ {s
i
})
and the disk corresponding to the maximum sensing
coverage range of s
i
.
DCNET 2010 - International Conference on Data Communication Networking
108

Corollary 4.3. For s
i
in S, if |X(s
i
,V(S))| < k, then
V(s
i
) is not k-covered.
The major advantages of these results is that we
can rely on simple Voronoi diagrams to deal with k-
coverage while the advanced model proposed in the
previous subsection is based on k-Voronoi tessella-
tions which are more complex to build. A more ac-
curate comparison between the two models will be
carried out in the simulation section.
4.3 Group Mobility Modeling
To enhance coverage while keeping more mobility
freedom, we suggest a group mobility model in which
ground sensors move in groups such that they pre-
serve k-coverage. To this purpose, for each mobil-
ity step, sensors define randomly groups of k mem-
bers for each which are not required to be the near-
est neighbors. Each group has a leader which defines
mobility steps. The remaining members of the group
take into account this choice to determine, in turn,
their next mobility step. By this manner, each sen-
sor’s mobility step depends on his integrating group.
Further,a sensor may movefrom one group to another
in each mobility step. This model enables the defini-
tion of overlapping k-Voronoi groups which increases
the guarantee to have a k-coverage. Thus, in the aim
to guarantee k-coverage all along the estimated target
path, the following model is defined:
• A group leader is elected from the set of the near-
est nodes to the estimated target path and after re-
ceiving a mobility instruction. The group leader
follows the mobility instruction sent by IS. Other-
wise, groups will move away from the target path.
• Each group leader is in charge of gathering group
members. It searches increasingly in its neighbor-
hood.
• A member chooses to belong to a group as long
as it does not receive a mobility instruction from
an IS. Otherwise, a mobility instruction is priori-
tized.
• For a mobility step, a member could only belong
to a single group. It may then move to another
group for further mobility steps.
• A node may act as a group leader as long as it
receives mobility instructions from the IS.
5 EXTENSION TO
MULTI-TARGET TRACKING
The advanced mobility model have defined the prob-
able zones of a target presence and drives sensors to-
wards these zones. Thus, a mobility instruction is
clearly defined and weighted according to the prob-
ability of the target presence. In the case of mul-
tiple targets, a sensor may receive different mobil-
ity instructions and then it chooses which to follow.
Nevertheless, this may lead to uneven sensors distri-
butions. Hence, some targets may be not sufficiently
covered especially when the number of sensors is not
enough to cover all the targets’ estimated locations.
For these reasons, we propose in the following two
techniques enabling the extension of the advanced
mobility model for multi-target tracking.
5.1 Extended Advanced Mobility Model
To guarantee the coverage of multiple targets, we
present the modifications introduced to the advanced
mobility model. In the presented mobility model, sen-
sors are free to define their next movement, two main
situations may be defined. In the first one, sensors
follow the mobility instruction driving to the target;
so, they move towards the probable zones of target
presence. In the second, a sensor chooses another dif-
ferent direction taking him away from these zones.
The main idea introduced for multi-target tracking is
that even when sensors are in the second situation,
they remain in nearby locations increasing the proba-
bility to return to the target direction in next mobility
steps. This can be fulfilled through the customization
of velocity according to the chosen direction in the
sense that sensor’s mobility velocity increases when
sensors moves towards target location and inversely.
For this reason, we define two velocity ranges. The
first, denoted by {V
hi
}, contains the high velocity val-
ues while the second, denoted by {V
li
}, contains the
low velocity values.
The extended advanced mobility model links the
sensor velocity to the chosen direction. Thus, mobil-
ity probability is defined as follows.
• The probability that a node chooses a given ve-
locity is equal to the probability to choose target
direction.
• When receiving mobility instructions, the direc-
tion of the nearest targets have the higher proba-
bility. Consequently, they are assigned the higher
probability velocity values.
• Three subsets of velocity values may be defined:
(1) a velocity valueV
t
enabling the sensor to reach
MOBILITY AND SECURITY MODELS FOR WIRELESS SENSOR NETWORKS USING VORONOI
TESSELLATIONS
109

the target position in the next mobility step; (2) a
velocity value from {V
hi
} when choosing the tar-
get direction but not sufficient to reach the target;
(3) a velocity value from {V
li
} when choosing an
other direction.
The underlying probability distribution is defined
as follows:
Pr
V
(v) =





P((r,α) = (r
t
,α
t
)) v = V
t
1
¯
V
hi
P((r,α) = (r
i
,α
i
)) v ∈ {V
hi
}
1
¯
V
li
(1− P((r,α) = (r
i
,α
i
)) v ∈ {V
li
}
5.2 Extended Mobility Model for
Multi-target Tracking
In the following, we divide the monitored zones into
regions related to the present targets. Let T be the
number of the tracked targets. In the following algo-
rithm, we identify the nearest sensors to each target.
Then, we move sensors such that target path remains
k-covered.
Algorithm 2: Extended group mobility model for multi-
target tracking.
While (number of sensors in target’s Delaunay trian-
gle ¿ threshold)
do
Compute T-Voronoi where T is the number of targets
Define the k-Voronoi in each T-cell
Apply the group mobility model in each cell
6 SENSOR ACTIVITY
SCHEDULING
In this section, we highlight the potential given by
Voronoi diagrams in implementing activity schedul-
ing strategies. We mainly show how sensors that do
not contribute effectively in enhancing the coverage
degree within a given zone can be detected and there-
fore turned-off for a laps of time.
Our idea is to exploit the properties of the Voronoi
tessellation to implement a distributed algorithm to
identify sensor nodes which sensing coverage is al-
ready covered by their neighbors. We first give the
definition of a redundant sensor.
Definition 6.1. A sensor s
i
∈ S is said to be redundant
if, and only if:
/
0 6= Γ(s
i
,R
s
i
)
\


[
s
j
∈Σ(s
i
)
Γ(s
j
,R
s
j
)


= Γ(s
i
,R
s
i
),
(8)
where Σ(s
i
) = {s ∈ S : Γ(s,R
s
) ∩ Γ(s
i
,R
s
) 6=
/
0 ∧ s 6=
s
i
}.
The interest, from the energy consumption opti-
mization point of view, of identifying redundant sen-
sors is obvious since such nodes can be turned-off. In
fact, the information provided by a redundant sensor
about the presence of a hostile target can be obtained
from its neighbors. In the rest of the section, we look
for a characterization of redundant sensor nodes.
The following proposition gives a necessary and
sufficient condition for node redundancy characteri-
zation.
Proposition 6.2. Let S be a set of sensor node po-
sitions in R
2
and X(s
i
) the set of intersection points
corresponding to s
i
∈ S. If s
i
is redundant if, and only
if:
X(s
i
,V(S)) ⊂
[
s
j
∈N(s
i
,V(S))
Γ(s
j
,R
s
j
). (9)
Proof. (i) Proof of ⇒: If a sensor s
i
is redundant, it
comes from Proposition 4.1 that:
N(s
i
,V(S)) ⊆ Σ(s
i
). (10)
Therefore, it can be written that:
[
s
j
∈N(s
i
,V(S))
Γ(s
j
,R
s
j
) ⊆
[
s
j
∈Σ(s
i
)
Γ(s
j
,R
s
j
). (11)
From Equations 8 and 11, it comes that if s
i
is redun-
dant then
Γ(s
i
,R
s
i
)
\


[
s
j
∈N(s
i
,V(S))
Γ(s
j
,R
s
j
)


= Γ(s
i
,R
s
i
).
Moreover, Equation 9 gives that X(s
i
,V(S)) ⊂
Γ(s
i
,R
s
i
). By transitivity of the inclusion operator, we
obtain:
X(s
i
,V(S)) ⊂
[
s
j
∈N(s
i
,V(S))
Γ(s
j
,R
s
j
).
(ii) Proof of ⇐: Trivial.
According to the proposition above, if there exists
x
j
∈ X(s
i
) such that x
j
/∈ Γ(s
i
,R
s
i
), then s
i
is not re-
dundant. Consequently, we propose an algorithm for
stating whether a node is redundant or not.
The following corollary extend the result of
Proposition 6.2 to the case where a k-coverage of the
monitored zone is needed. Obviously, the definition
of redundancyshould be slightly modified in this case
to encompass sensor nodes whose sensing coverage is
totally k-covered.
Corollary 6.3. Let s
i
in S be a sen-
sor node. For every x
j
in X(s
i
,V(S)), if
|{x
j
}
T

S
s
k
∈N(s
i
,V(S\{s
i
})
Γ(s
k
,R
s
i
)

| < k, then
s
i
is not redundant.
DCNET 2010 - International Conference on Data Communication Networking
110

Algorithm 3: Redundant sensor discovery.
∀s
i
∈ S
{ Compute N(s
i
,V(S));
Generate V(N(s
i
,V(S)) \ {s
i
}));
Compute X(s
i
,V(N(s
i
,V(S)) \ {s
i
})));
∀x
j
∈ X(s
i
,V(N(s
i
,V(S)) \ {s
i
})))
{ r:=0;
∀s
k
∈ N(s
i
,V(S))
{ if (x
j
/∈ Γ(s
k
,R
s
i
)) then
r:=1; } }
if (r=1) then
s
i
is not redundant;
else
s
i
is redundant; }
Using this corollary, the strategy defined in the
above algorithm remains effective in sensitive con-
texts where the monitored area should be k-covered.
7 K-SECURITY IN WIRELESS
SENSOR NETWORKS
In this section, we will build on the security model
presented in (Sliti et al., 2008) to inroduce an opti-
mized k−security model. For this purpose, we use
higher-order Voronoi diagrams to develop a k out of
n threshold signature scheme. It allows any subset of
k sensor nodes defined in a voronoi cell to generate a
valid signature. Conversely, any subset of k
′
individ-
ual signatures does not constitute a valid signature if
k
′
< k. In fact, since the monitored zone is subdivided
into Voronoi tesselation, each k−Voronoi cell defines
the nearest region to its k generators which means that
an eventualevent occuring in this region should be de-
tected by the k sensors.
In the following, we extend the well-known Shoup
threshold cryptosystem (Shoup, 2000) to the elliptic
curve context.
Let F
p
be a prime finite field so that p is a prime
number and let a,b ∈ F
p
satisfying 4a
3
+ 27b
2
6= 0.
An elliptic curve E
p
(a,b) over F
p
is defined by the set
of solutions of the following equation (called Weier-
strass equation):
y
2
≡ x
3
+ ax+ b(mod p), (12)
together with an extra point O called the point at
infinity.
Cryptographic schemes based on ECC rely on
scalar multiplication of elliptic curve points. Given
an integer r and a point P ∈ E
p
(a,b), scalar multipli-
cation is the process of adding P to itself r times. The
result of this scalar multiplication is denoted r.P.
7.1 Distributed Key Management
Scheme
To implement the prposed k−security model, the sen-
sor network should be nriched by a Public Key In-
frastructure (PKI) that will be in charge of managing
the keys ans the certificates used in the various signa-
ture management phases. The basic PKI parameters,
including the number of CAs, the trust relationships
between these CAs, as well as the certificate lifetime
will obviously vary according to the features of the
monitored battlefield and the nature of the military
mission. As far as we are concerned, we illustrate
the differentcryptographicfunctionnalitiesin the sim-
ple case where only one CA is considered. In fact,
these functionnalities should not change when being
applied in a generic context where multiple CAs may
be considered.
Key Generation
The key generation phase is performed by the CA as
follows:
- generate randomly two large primes p,q ∈ P,
where P is the set of prime integers, and p = 2p
′
+ 1,
q = 2q
′
+1, with p
′
and q
′
are themselves primes. De-
note t = pq and m = p
′
q
′
.
- generate the public exponent e ∈ P such that e >
n (n is the number of private keys). The public key is
π = (t,e).
- compute d ∈ Z such that de de ≡ 1modm.
- build the polynomial f(X) =
∑
k−1
i=0
a
i
X
i
∈ Z[X]
such that f(0) = d.
- compute, for 1 ≤ i ≤ n, κ
i
= f(i)modm. The
integer κ
i
is the private key of sensor node s
i
.
Key Revocation
Key revocation may occur in two cases:
1. The sensor node is physically accessed by unau-
thorized party. In this case, th sensor node should
ask for the revocation of its certificate before trig-
gering the tamper-proof functionnalities. To this
end, a secret parameter that should have been pre-
loaded by the CA before the deployment of the
WSN should have been sent to the CA in oreder
to revoke the corresponding certificate. Once this
task has been successfully conducted, the critical
components of the sensor node are intentionally
self-destructed.
2. The sensor node is suspected to be compromised.
The suspected node should first be probed to state
whether it consists in an intruder node that has
spoofed the identity of the legitimate node or it
MOBILITY AND SECURITY MODELS FOR WIRELESS SENSOR NETWORKS USING VORONOI
TESSELLATIONS
111

is a sensor node that has fallen under the con-
trol of non-authorized parties. To this purpose,
challenge-response authentication messages and
radio fingerprinting can be used. If the suspected
node is a compromised one, a tolerance state,
where the sensor node can forward packets with-
out issuing alert messages, isinitiated. During this
state, the behavior of the potentially compromized
node is monitored to detect the anomalies that it
may generate. At the end of the tolerance inter-
val, the suspected node is either rehabilited or irre-
versibly discarded. From the certificate manage-
ment point of view, this pre-supposes that during
the tolerance state, the certificate of the suspected
node is suspended (i.e. subjected to a temporary
revocation). In addition, when the node is irre-
versibly de-activated, the certificate is definitively
revoked.
Key Renewal
It may occur that some sensor nodes are recuperated
and used for future surveillance missions. In such
cases, the key credentials are removedfrom the sensor
nodes and once the old certificate has been checked
for revocation, the CA generates a new private key
for the node of interest and uploads the correspond-
ing certificate in a physically protected zone of the
storage memory.
Key Distribution
Unlike traditional PKI frameworks, only one key dis-
tribution scheme is considered in our context. It
consists in the secure physical upload of the cryp-
tographic credentials by the CA. To implement this
scheme a secure procedure letting the CA access-
ing the sensitive zones of the non-volatile memory of
the sensor node should be available. This procedure
should be made available by the manufacturer and the
underlying access credentials should be submitted di-
rectly to the CA.
7.2 Intermediate Signature Generation
and Verification Phase
An event V that may be related to the detection of a
hostile target must be converted to a point P = (v
1
,v
2
)
in E
m
(a,b). The conversion of a message to an ECC
point is done according to the approach proposed in
(Hankerson et al., 2004). Then, a sensor node s
i
can
generate its individual signature (σ
x
i
,σ
y
i
) using its pri-
vate key according to the following equation.
(σ
x
i
,σ
y
i
) = 2n!κ
i
(v
1
,v
2
)modm.
This signature will then be forwarded to the cor-
responding core sensor through a set of relay nodes
(belonging to the sensing layer) denoted by R =
{r
1
,..,r
u
} ⊆ {s
1
,..,s
n
}. An important functionality
that could be implemented by the relaying sensors is
to identify and withdraw false alert messages. This
feature is called intermediate verification. We sup-
pose that a secret integer γ is broadcasted by the core
node (this broadcast should be enciphered using a
threshold encryption algorithm). Hence, node s
i
com-
putes the point
˜
P = γ.(σ
x
i
,σ
y
i
)mod t. Instead of send-
ing only the signed message to the core sensor, s
i
also
sends the integer ω, which stands for the order of
˜
P
(i.e., ω.
˜
P = O).
To check the validity of an individual signature,
node r
j
∈ R calculates the point Q as follows.
Q = ωγ.(σ
x
i
,σ
y
i
)mod t. (13)
The verification succeeds if, and only if, Q = O.
Clearly, the robustness of the intermediate verifi-
cation scheme builds upon the complexity, for the in-
truder, to determine γ. Effectively,computing γ know-
ing (σ
x
i
,σ
y
i
) and ω involves discrete logarithm compu-
tation within E
t
(a,b). This problem has been shown
to be intractable in (SEC 1, 2000).
7.3 k-Vornoi Cell Signature Verification
Supposing that a core sensor has collected k signa-
tures generated by a subset of sensor nodes (s
i
)
i∈S
,
where S = {i
1
,..,i
k
}, the objectiveis to verifywhether
all these signatures are valid. To this purpose, we
compute:
w = Σ
k
i=1
2.λ
0,i
.(σ
x
i
,σ
y
i
)mod t,
where
λ
S
i, j
= n!
Π
j
′
∈S
(i− j
′
)
Π
j
′
∈S
( j − j
′
)
.
To verify the validity of the global signature, the
core sensor checks if:
ew = 4n!
2
(v
1
,v
2
)modt (14)
A proof of correctness is given in the following.
We first develop the expression of w.
w = 4n!Σ
k
i=1
λ
0,i
j
( f(i)modm)(v
1
,v
2
)modt
From the properties of the determinant of the Van-
dermonde matrix, we obtain:
n! f(i) = Σ
j∈S
λ
S
i, j
f( j)modm.
Therefore, it can be written that:
w = 4n!
2
f(0)(v
1
,v
2
)modt = 4n!
2
d (v
1
,v
2
)modt
ew = 4n!
2
(v
1
,v
2
)modt.
DCNET 2010 - International Conference on Data Communication Networking
112

8 CONCLUSIONS AND
POTENTIAL EXTENSIONS
This paper presented two Voronoi-based mobility
models for target tracking using WSNs. The key ad-
vantage of these models is that they encompass the
potential target position in the construction of the mo-
bility instructions. This ensures that the locations
where the target is most probable to be are more cov-
ered than the rest of the monitored area. We also pro-
posed a redundancy discovery technique to enhance
the WSN cost-effectiveness. An enhancement of this
work to build a multi-target tracking framework is
currently under development.
REFERENCES
C. Gui and P. Mohapatra, ”Power Conservation and Quality
of Surveillance in Target Tracking Sensor Networks,”
Proc. ACM MobiCom ’04, pp. 129-143, Sept. 2004.
M. Hamdi, N. Boudriga, M. S. Obaidat, WHOMoVeS:
An optimized broadband sensor network for military
vehicle tracking, International Journal of Commu-
nication Systems, Vol. 21 , Issue 3, pp. 277-300,
ISSN:1074-5351, 2008.
L. Wang, H. Shen, Z. Chen, and Y. Lin, Voronoi Tessel-
lation Based Rapid Coverage Decision Algorithm for
Wireless Sensor Networks, Lecture Notes in Com-
puter Science, Ubiquitous Intelligence and Comput-
ing, Springer, 2007.
I. Stojmenovic, A. K. Ruhil, D.K. Lobiyal, Voronoi Dia-
gram and Convex Hull Based Geocasting and Routing
in Wireless Networks, Proceedings of the Eighth IEEE
International Symposium on Computers and Commu-
nication (ISCC03), KEMER - ANTALYA, Turkey,
2003.
Marcos Augusto M. Vieira, Luiz Filipe M. Vieira, Linnyer
B. Ruiz, Antonio A. F. Loureiro, Antonio O. Fernan-
des, Nogueira Nogueira, Scheduling Nodes in Wire-
less Sensor Networks: A Voronoi Approach, lcn, p.
423, 28th Annual IEEE International Conference on
Local Computer Networks (LCN’03), 2003.
W. Wang, V. Srinivasan, and K-C. Chua, Trade-offs Be-
tween Mobility and Density for Coverage in Wireless
Sensor Networks, MobiCom07, September 914, 2007,
Montral, Qubec, Canada.
M. Sliti, M. Hamdi, N. Boudriga. An Elliptic Threshold Sig-
nature Framework for k-Security in Wireless Sensor
Networks, ICECS, 2008.
V. Shoup, Practical Threshold Signatures Proc, Int’l Conf.
Theory and Application of Cryptographic Techniques
(EUROCRYPT ’00), 2000.
D. Hankerson, A. Menezes, and S. Vanstone, Guide to El-
liptic Curve Cryptography, Springer, 2004.
Standards for Efficient Cryptography, SEC 1: Elliptic Curve
Cryptography, Version 1.0, September 2000.
MOBILITY AND SECURITY MODELS FOR WIRELESS SENSOR NETWORKS USING VORONOI
TESSELLATIONS
113