
PRACTICAL EXAMPLES OF GPU COMPUTING
OPTIMIZATION PRINCIPLES
Patrik Goorts
1
, Sammy Rogmans
1,2
, Steven Vanden Eynde
3
and Philippe Bekaert
1
1
Hasselt University - tUL - IBBT, Expertise Centre for Digital Media, Wetenschapspark 2, BE-3590 Diepenbeek, Belgium
2
Multimedia Group, IMEC, Kapeldreef 75, BE-3001 Leuven, Belgium
3
Lessius Hogeschool – Campus De Nayer, J. De Nayerlaan 5, BE-2860 Sint Katelijne Waver, Belgium
Keywords:
CUDA, GPGPU, Optimization principles, Visual computing, Fermi.
Abstract:
In this paper, we provide examples to optimize signal processing or visual computing algorithms written for
SIMT-based GPU architectures. These implementations demonstrate the optimizations for CUDA or its suc-
cessors OpenCL and DirectCompute. We discuss the effect and optimization principles of memory coalescing,
bandwidth reduction, processor occupancy, bank conflict reduction, local memory elimination and instruction
optimization. The effect of the optimization steps are illustrated by state-of-the-art examples. A comparison
with optimized and unoptimized algorithms is provided. A first example discusses the construction of joint
histograms using shared memory, where optimizations lead to a significant speedup compared to the original
implementation. A second example presents convolution and the acquired results.
1 INTRODUCTION
In the last years, generic parallel computing on graph-
ical devices is becoming popular for versatile prob-
lems. GPUs are used in generic visual computing
and games, but also in medical fields (Shams et al.,
2010), biology (Phillips et al., 2005), physics and
many more. Thanks to the great interest in off-the-
shelf parallel devices, a lot of research and work is
conducted to enable ease of programming of graph-
ical devices. These advances remove the need to
map every problem to a visual representation process-
able by the graphical pipeline. With the introduc-
tion of CUDA (NVIDIA, 2010), it is possible to use
generic instructions on a parallel device; no graphi-
cal pipeline is used. While CUDA eases the use of
GPUs for parallel computation, the efficient program-
ming is still difficult. Due to the different limitations
and the memory hierarchy, very fast execution is pos-
sible, but some effort must be made to maximize the
performance.
In this paper, we will investigate some considera-
tions when implementing computer vision algorithms
on CUDA-enabled devices. These algorithms typi-
cally need a lot of memory to store and save data.
The copying of these data between on-chip and off-
chip memory can take more time than the actual cal-
culations, as stated by the infamous memory wall
(Asanovic et al., 2006). To tackle this problem, spe-
cial care should be taken to efficiently perform mem-
ory operations.
Another less-known problem includes the access
strategy of on-chip memory. While the access time
is short, multiple threads shall access the memory si-
multaneously. This simultaneous access can signif-
icantly reduce performance. This kind of optimiza-
tions is less documented and investigated. We applied
the reduction of these so-called bank conflicts to two
examples and reduced the execution time.
We will provide examples where all of this opti-
mizations are effective. These examples demonstrate
the importance of optimizations which are often for-
gotten in state-of-the-art algorithms. We will focus on
CUDA-enabled devices, but these optimizations still
hold for OpenCL (Munshi, 2008) and DirectCompute
(Boyd, 2008), as these use the same execution model
as CUDA.
The paper is divided as follow: in section 2 we
will provide a general overview to optimize the par-
allel execution of algorithms on SIMT-based archi-
tectures and section 3 will provide some optimization
examples. We will conclude in section 4.
46
Goorts P., Rogmans S., Vanden Eynde S. and Bekaert P. (2010).
PRACTICAL EXAMPLES OF GPU COMPUTING OPTIMIZATION PRINCIPLES.
In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 46-49
DOI: 10.5220/0002990400460049
Copyright
c
SciTePress

2 PARALLELIZATION OF
ALGORITHMS
In this section, we will provide an overview to op-
timize algorithms implemented on SIMT architec-
tures. The first step is the division of the algorithm in
threads. Threads should be chosen to reduce the com-
munication between them. CUDA allows fast com-
munication through shared memory, but global com-
munication is slow and unsynchronized. However,
using shared memory can reduce redundant mem-
ory reads and improve performance. After defining
threads, these must be grouped in blocks. These
choices must be made according to the code optimiza-
tion guidelines, including:
1. Global Memory Coalescing. Optimize off-chip
memory access by grouping successive memory
loads in one instruction. The memory bus is less
occupated, thus allowing more throughput.
2. Global Memory Bandwidth Reduction. Reduce
total amount of memory requirements.
3. Increasing Occupancy. Use more processing
power simultaneously by defining enough threads
to keep every processor busy.
4. Reduce Bank Conflicts. Optimize on-chip mem-
ory access by avoiding operations in the same
memory segment (bank).
5. Eliminate Local Memory Usage. Reduce costly
register swapping to slow off-chip memory.
6. Optimize Instructions. Reduce clock cycles of
the calculations.
These principles go further than previous research
(Ryoo et al., 2008), providing more low-level and of-
ten forgotten strategies.
3 OPTIMIZATION EXAMPLES
In this section we will provide two state-of-the-art
examples where optimization increased the perfor-
mance. The first example calculates joint histograms
based on the method of (Shams and Kennedy, 2007).
The second example investigates the effect of coalesc-
ing and bank conflicts on convolution calculation and
is based on the work described in (Goorts et al., 2009).
3.1 Joint Histogram Calculations
We will now provide an example of a visual comput-
ing algorithm parallelized with a SIMT architecture,
the calculation of joint histograms. Given two images
Figure 1: Calculation of a joint histogram. The pixel value
in the first image and the corresponding pixel value in the
second image defines which position in the joint histogram
should be updated. (a) Example of a joint histogram. (b)
Matrix representation.
with given pixel correspondences, a 2D histogram is
created. For every pixel in the first image and the
corresponding pixel in the second image, a greyvalue
pair is obtained. The 2D histogram counts the occur-
rence of every pair (see figure 1). Joint histograms are
widely used in image registration algorithms.
Dividing the calculation of joint histograms in
threads is possible in different ways. A thread can
process a pair of greyvalues and fill in the histogram,
or a thread can process a field in the histogram and
counting the corresponding pairs in the image. In the
former case every thread must have write-access to
every element in the histogram and a concurrent write
system must be provided. In the latter case every
thread must read the full image, and as a consequence
the algorithm doesn’t scale well for large images.
The implementation used here is described in
(Shams and Kennedy, 2007). This method uses a
histogram per warp (16 concurrent running threads),
located in shared memory, producing subhistograms.
These subhistograms are added together first at block
level and later globally in a second kernel. Because
threads in the same warp can access the same memory
location, some write protection must be provided. In
(Shams and Kennedy, 2007), this problem is solved
by tagging the values with the thread ID. The writ-
ten values are read again after the write, and the tag
is compared. If the tag is wrong, another thread has
written its value and the write will be retried. Eventu-
ally, every thread will have updated the memory loca-
tion.
PRACTICAL EXAMPLES OF GPU COMPUTING OPTIMIZATION PRINCIPLES
47

Table 1: Results of joint histogram calculations.
Implementation Time
Original implementation 350 msec
Optimized implementation (atomic) 196 msec
Optimized implementation (tagged) 190 msec
int bin = ...;
unsigned int tagged;
do
{
\\ Remove previous tag
unsigned int val =
localHistogram[bin] & 0x07FFFFFF;
\\ Tag the value with the thread id
tagged = (threadid << 27) | (val + 1);
\\ Write to the histogram
localHistogram[bin] = tagged;
} while (localHistogram[bin] != tagged);
\vspace{-0.3cm}
This method was originally developed before
atomic operations in shared memory were provided.
Here, we will investigate the original method, but us-
ing these atomic operations and other optimization
techniques.
We have performed joint histogram calculations
of images of size 4096x4096 on a NVIDIA GTX 280
with 30 multiprocessors, a clock speed of 1.3 GHz
and 1 GiB of off-chip memory. As shown in Ta-
ble 1, the version of (Shams and Kennedy, 2007) is
more efficient when using optimization techniques.
More specifically, we have reduced the size of the data
to speed up memory reads, enabled colaesced loads
and decreased bank conflicts. These optimizations
can be accomplished by rearranging the threads, and
thus control the memory operations per thread. Ad-
ditionally, we have modified the calculation instruc-
tions to reduce registry usage and thus reduce register
swappng to global memory. By using these optimiza-
tions, we accomplished a speedup of 150 msec, which
demonstrates the importance of attention to optimiza-
tion.
Using atomic add operations on shared memory
to remove the tagging technique does not result in
faster execution. This demonstrates that care should
be taken when using atomic operations, even in small
kernels, and other techniques should be implemented
and benchmarked if possible.
3.2 Convolution
Convolution is an image processing method where
for every pixel a new pixel value is calculated in
function of the values surrounding the current pixel.
Convolution is often referred to as finite impulse re-
sponse filtering. Effects of block sizes and imple-
mentation strategies are extensively investigated in
(Goorts et al., 2009). Here, we will discuss the im-
portance of the position of threads to enable coalesc-
ing and reduce bank conflicts. We will only consider
normal convolution algorithms; techniques using fast
Fourier transformations and singular value decompo-
sitions are not in the scope of this paper.
One thread per pixel is assigned. Every thread
now needs the value of the surrounding pixels, re-
quiring to load multiple pixels from off-chip mem-
ory. Because threads in the same block have a shared
memory, it is possible to use the data read by other
threads and thus enabling data reuse to reduce mem-
ory reads. However, threads at the border of the block
do not have sufficient data available and therefore a
border of threads is created to read the missing data.
This border is called the apron. Because these threads
do not calculate new output, the pixels located in the
apron must be read by different blocks. These redun-
dant reads must be reduced to a minimum.
Because of the apron, it is not sufficient to use
blocks with the for coalescing required width of a
multiple of 16. The width of the apron must also
be a multiple of 16 (see figure 2) to enable coalesc-
ing in every block. By doing this, we will create a
lot of unnecessary threads, but the performance will
increase thanks to coalesced memory operations and
the elimination of bank conflicts. This result is visi-
ble in figure 3. The results are dependent on the filter
size; the larger the filter, the larger the apron. Be-
cause the non-coalesced algorithm must read every
word in the apron apart, the memory instructions will
increase if the apron size increases. In the coalesced
case, the read instructions stay constant and optimal.
There will be more thread and more blocks, but the
performance is still higher, which proves the impor-
tance of coalescing in this application. Because the
thread positions are chosen correctly, bank conflicts
are removed from the coalesced case.
4 CONCLUSIONS
We have applied optimization principles to increase
the performance of algorithms executed on SIMT ar-
chitectures. By coalescing off-chip memory loads,
reducing bandwidth, increasing occupancy, reducing
bank conflicts, eliminating local memory usage and
optimizing instructions, one can maximize the utiliza-
tion of the resources of the parallel device and reduce
execution time. Reducing bank conflicts is forgotten
SIGMAP 2010 - International Conference on Signal Processing and Multimedia Applications
48
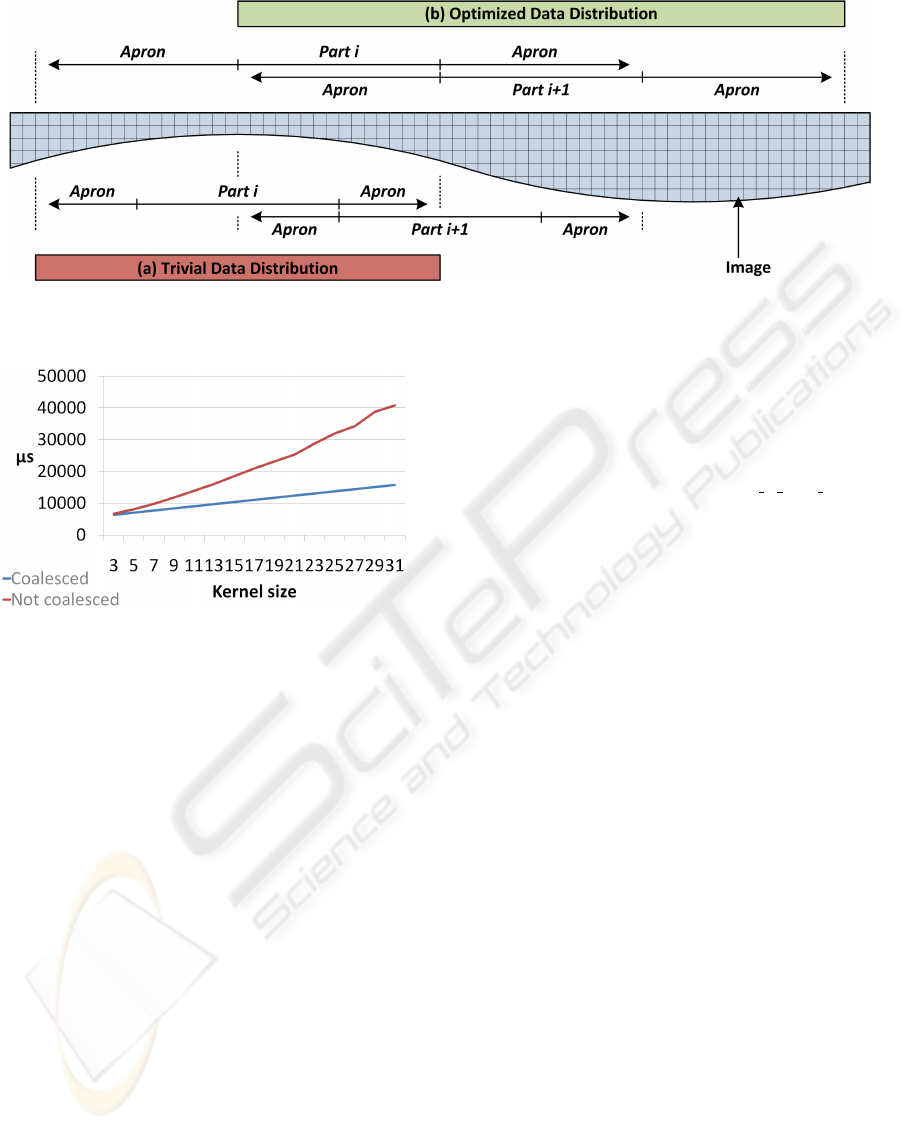
Figure 2: Alignment of the threads when performing convolution. The apron is a multiple of 16 to enable coalescing in all
blocks.
Figure 3: Horizontal convolution of a 4096x4096 image
with different filter sizes. The importance of coalescing
increases if the filter sizes increase; bigger filters require
larger aprons with more uncoalesced reads and more mem-
ory operations, while the coalesced algorithm requires only
one read per 16 words.
by most programmers, but these can increase perfor-
mance significantly. We have demonstrated the effec-
tiveness of the optimizations with two state-of-the-art
examples.
REFERENCES
Asanovic, K., Bodik, R., Catanzaro, B. C., Gebis, J. J.,
Husbands, P., Keutzer, K., Patterson, D. A., Plishker,
W. L., Shalf, J., Williams, S. W., and Yelick, K. A.
(2006). The Landscape of Parallel Computing Re-
search: A View From Berkeley. Electrical Engineer-
ing and Computer Sciences, University of California
at Berkeley, 18(183):19.
Boyd, C. (2008). The DirectX 11 Compute Shader. Shading
Course SIGGRAPH.
Goorts, P., Rogmans, S., and Bekaert, P. (2009). Optimal
data distribution for versatile finite impulse response
filtering on next-generation graphics hardware using
cuda. Parallel and Distributed Systems, International
Conference on, pages 300–307.
Munshi, A. (2008). OpenCL: Parallel Computing on the
GPU and CPU. Shading Course SIGGRAPH.
NVIDIA (2010). What is cuda?
http://www.nvidia.com/object/what is cuda new.html.
Phillips, J. C., Braun, R., Wang, W., Gumbart, J., Tajkhor-
shid, E., Villa, E., Chipot, C., Skeel, R. D., Kal, L.,
and Schulten, K. (2005). Scalable molecular dynam-
ics with namd. Journal of Computational Chemistry,
26(16):1781–1802.
Ryoo, S., Rodrigues, C. I., Baghsorkhi, S. S., Stone, S. S.,
Kirk, D. B., and mei W. Hwu, W. (2008). Optimiza-
tion principles and application performance evalua-
tion of a multithreaded gpu using cuda. In PPOPP,
pages 73–82.
Shams, R. and Kennedy, R. A. (2007). Efficient histogram
algorithms for NVIDIA CUDA compatible devices.
In Proc. Int. Conf. on Signal Processing and Com-
munications Systems (ICSPCS), pages 418–422, Gold
Coast, Australia.
Shams, R., Sadeghi, P., Kennedy, R. A., and Hartley, R. I.
(2010). A survey of medical image registration on
multicore and the GPU. IEEE Signal Processing Mag.
(to appear).
PRACTICAL EXAMPLES OF GPU COMPUTING OPTIMIZATION PRINCIPLES
49
