ANONYMOUS BUT AUTHORIZED TRANSACTIONS SUPPORTING

SELECTIVE TRACEABILITY

Daniel Slamanig

and Stefan Rass

Department of Medical Information Technology, Healthcare IT & Information Security Group

Carinthia University of Applied Sciences, 9020 Klagenfurt, Austria

Institute of Applied Informatics, System Security Group, Klagenfurt University, 9020 Klagenfurt, Austria

Keywords:

Anonymity, Privacy, Anonymous authentication, Anonymous transactions, Public-key encryption, One-show

tokens, Blind signatures.

Abstract:

While privacy was more or less neglected in the early days of the Internet, in recent years it has emerged to

be a hot topic in computer security research. Among other reasons, since the use of the Internet is becoming

more and more ubiquitous, cloud computing emerges and consequently users provide a lot of information to

potentially untrusted third parties. In this paper we propose an approach which provides a means for users to

anonymously conduct transactions with a service-provider such that those transactions can neither be linked to

a speciﬁc user nor linked together. At the same time, a service-provider can be sure that only authorized users

are able to conduct transactions. In particular, we bring together the concepts of anonymous authentication

from public-key encryption and anonymous as well as unlinkable token based transactions in order to proﬁt

from the advantages of the two single approaches. Since full anonymity is usually not desirable, we provide

mechanism to identify misbehaving anonymous users behind transactions. More precisely, we realize selective

traceability, which allows revocation of the anonymity of a suspicious users along with the identiﬁcation of

all of her transactions, without violating the privacy of all remaining users.

1 INTRODUCTION

Today, many services and applications are provided

via the Internet resulting in advantageous “anytime,

anywhere” access for users. However, privacy be-

comes a major concern, and its protection is chal-

lenging in several ways. Ideally, a user is able to

conduct transactions with a service-provider in a way

such that a transaction cannot be assigned to an iden-

tity (anonymity), nor may two or more transactions

be related to each other efﬁciently (unlinkability). On

the other hand, preserving security for the provider re-

quires that only authorized users are able to consume

a service and users can be revoked in case of suspi-

cion (traceability).

Interesting applications are in the ﬁeld of cloud-

computing and especially if even seemingly harmless

information about the service-usage behavior, e.g.

access frequencies, frequencies of transactions, ac-

cessed content, can be valuable information for the

service or the cloud provider and needs to be pro-

tected from those insiders and wiretappers. One il-

lustrative example is within the healthcare domain,

where applications allowing the management of very

sensitive health-information for everyone via the In-

ternet, so called Personal Health Records, are grow-

ing rapidly (e.g. Google Health, Microsoft Health

Vault). In this context, such information can reveal

a lot about the state of health of a speciﬁc person,

e.g. access frequencies will correlate with the state

of health. Hence, if such information are available

for instance to human resource managers, this could

massively inﬂuence the chances of getting a job.

1.1 Contribution

In this paper we propose an approach to realize

anonymous and unlinkable, but authorized service us-

age based on a combination of anonymous authentica-

tion from public-key encryption and one-show tokens

obtained from blind signatures. Our approach is espe-

cially applicable for services with many users, which

dynamically join and leave a service, and frequently

conduct transactions with a service-provider. Further-

more, our proposed construction achieves all aspects

discussed in the introduction at very low computa-

132

Slamanig D. and Rass S. (2010).

ANONYMOUS BUT AUTHORIZED TRANSACTIONS SUPPORTING SELECTIVE TRACEABILITY.

In Proceedings of the International Conference on Security and Cryptography, pages 132-141

DOI: 10.5220/0002994501320141

 SciTePress

tional overhead, whilst coming at negligible cost for

implementation, as only standard (and already widely

implemented) public-key cryptography and state of

the art smart-cards are used. This is especially of

interest, since public-key infrastructures are widely

available today.

Our contributions in this paper are manifold.

Firstly, we introduce a novel paradigm called postac-

tive anonymous authentication from public-key en-

cryption, which allows us to realize anonymous au-

thentication at the cost of a single decryption for

users, in contrast to O(n) decryption resp. encryp-

tion operations for schemes known so far. Thereby n

is the number of users, the so called anonymity-set.

Secondly, we introduce a combination of anonymous

authentication from public-key encryption and anony-

mous one-show tokens from blind signatures. Finally,

we present several extensions to one-show tokens in-

cluding ﬁne-grained validity periods and most notable

selective traceability. The latter propertymeans, that a

trusted traceability authority is able to link all transac-

tions of a suspicious anonymous user as well as iden-

tify this user, without violating the privacy of the re-

maining users.

1.2 Intuition behind our Construction

In a nutshell, our construction is as follows. A

user registers with a service-provider by providing

a public-key of a public-key encryption scheme and

registers with a traceability authority. Additionally,

we assume that user’s are in possession of a tamper

resistant smart-card. The service-provider maintains

a directory D of these public-keys along with a valid-

ity of service usage. Users anonymously authenticate

against a subset of users in this directory and if the

authentication succeeds they obtain a blind signature

for a token. On presenting a valid token-signature pair

along with a query for a service, the service-provider

checks whether the signature is valid, the token was

not already used and is valid for the current time-

period. If all these checks hold, he responds with the

answer to the query. Simultaneously, he issues a blind

signature for a new token. Consequently, users can

conduct sequences of transactions with the service-

provider. If suspicion occurs, the service-provider can

give the token corresponding to a suspicious transac-

tion and the blacklist containing already spent tokens

to a traceability authority, who in turn is able to (1)

identify the respective user and (2) ﬁnd all transac-

tions of this user without violating the anonymity of

other users (opening tokens of other users). Note, that

all actions of users are anonymous and unlinkable.

2 RELATED WORK

Several token-based approaches have been proposed

so far, although having in mind quite diverge appli-

cations. The most prominent are anonymous creden-

tial systems introduced in (Chaum, 1985). The basic

idea is that users are able to obtain credentials (to-

kens) for different pseudonyms from different orga-

nizations and can prove the possession of these cre-

dentials without revealing anything more than the fact

that they own such credentials. Over the years there

have been proposed different approaches to design

anonymous credential systems providing quite dif-

ferent functionalities (Lysyanskaya et al., 2000; Ca-

menisch and Lysyanskaya, 2001; Verheul, 2001). Al-

though anonymous credential systems are very pow-

erful, realizing identity-escrow, limiting the number

of showings as well as realizing dynamical joining

and revoking of users comes at high computational

costs. Furthermore, we do not focus on systems that

involve multiple credential (token) issuers and veri-

ﬁers and are looking for more efﬁcient solutions.

Another class of schemes are multi-coupon (MC)

systems (Canard et al., 2006; Chen et al., 2007),

whereas a MC represents a collection of coupons

(or tokens) that is regarded as a single unit. Ba-

sically, a user is issued a batch of tokens (which

are tied together) and is allowed to spend one to-

ken after another in an anonymous and unlinkable

fashion. The most sophisticated schemes (Canard

et al., 2006; Chen et al., 2007) are based on signa-

ture schemes that allow users to obtain signatures on

(committed) sequences of messages and provide ef-

ﬁcient zero-knowledge proofs of knowledge of sig-

natures and properties of signed message elements

(Camenisch and Lysyanskaya, 2002; Camenisch and

Lysyanskaya, 2004). Although these schemes are

conceptually very elegant, they are quite expensive

and do not provide (selective) traceability.

Recently, a scheme for anonymous subscriptions,

based on one of those signature schemes was pro-

posed in (Blanton, 2008). The concept is very ap-

pealing and it provides an elegant solution to re-

alize validity-periods of subscriptions using zero-

knowledge range proofs, but it does not support (se-

lective) traceability, which is an important feature

of our construction. Another construction of (Ca-

menisch et al., 2006) focuses on n-times anonymous

authentication, which allows to identify a user if he

spends more than n tokens within one time-period.

However, they also do not focus on selective trace-

ability.

To the best of our knowledge, the only solution

to selective traceability so far are traceable signatures

ANONYMOUS BUT AUTHORIZED TRANSACTIONS SUPPORTING SELECTIVE TRACEABILITY

133

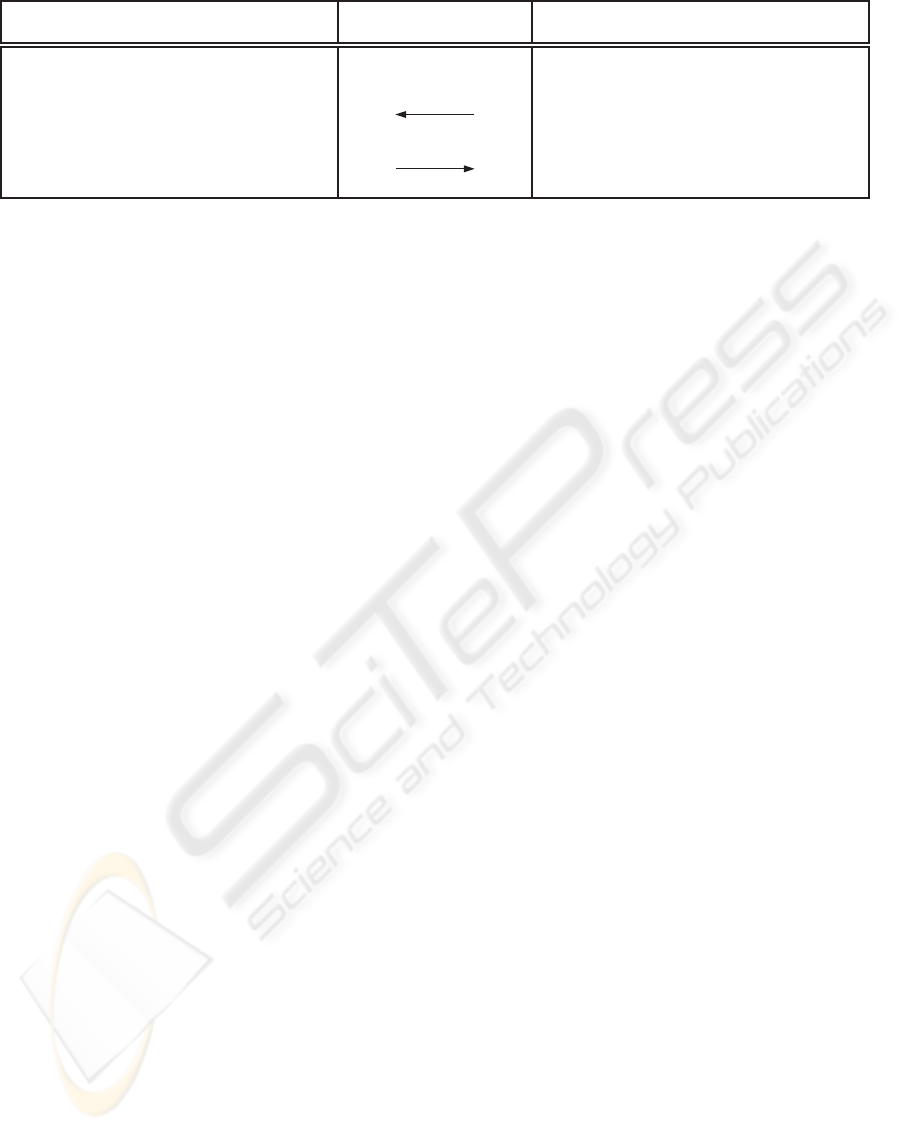
User Veriﬁer

c ∈

{0,1}

c = (E

(c),.. . ,E

(c))

′

= D

(c[i])

′

= c

Protocol 1: Anonymous authentication from PKE.

(Kiayias et al., 2004; Libert and Yung, 2009), which

are, however, rather of theoretical interest. In con-

clusion, none of the aforementioned approaches pro-

vides an efﬁcient way to realize selective traceabil-

ity, whereas our construction presented in this paper

achieves this goal at a reasonable overall cost.

3 POSTACTIVE ANONYMOUS

AUTHENTICATION

In this section we present a novel paradigm for

anonymous authentication schemes from public-key

encryption (PKE), which we call postactive anony-

mous authentication. Anonymous authentication

from public-key encryption and its application is not

absolutely new (Schechter et al., 1999; Lindell, 2007;

Xi et al., 2008; Slamanig et al., 2009), but allows a

convenient way for a prover to anonymously authen-

ticate to a veriﬁer providing user-chosen bandwidth-

anonymity trade off. More precisely, users can deter-

mine on their own the size of the anonymity-set (as

a subset of all users) and consequently determine the

bandwidth consumption of the protocol (see below).

3.1 Deterministic from Probabilistic

Public-key Encryption

The notion of deterministic public-key encryption

was introduced in (Bellare et al., 2007). Basically,

the idea behind this concept is to turn any probabilis-

tic PKE into a deterministic scheme. One general

and efﬁcient construction is the so called “Encrypt-

with-Hash” (EwH) construction introduced in (Bel-

lare et al., 2007), which will be discussed subse-

quently. An EwH scheme is based on a probabilistic

PKE scheme and deterministically encrypts a plain-

text m by applying the encryption algorithm of the

probabilistic scheme, whereas the used random coins

ω are not chosen uniformly at random, but are com-

puted as a hash of the public key PK and the plain-

text m. Consequently, everybody who knows a mes-

sage m and a ciphertext c (presumably an encryption

of m), can deterministically infer the random coins

used for the encryption, i.e. compute ω = H(PK, m)

and c

∗

= E

(m;ω) and check whether the encryp-

tion c

∗

computed by him equals the given ciphertext.

If c

∗

= c holds, they are both encryptions of the same

message m. It should be noted that the output of the

hash-function needs to be suitable for the use as ran-

dom coins in the respective PKE scheme.

3.2 Anonymous Authentication from

Public-key Encryption

Loosely spoken, the basic idea behind anonymous au-

thentication protocols is that a veriﬁer runs n paral-

lel instances of a challenge-response protocol based

on public-key encryption using n distinct public keys

with one anonymous prover, who represents n “vir-

tual” provers (we call this set the anonymity-set).

Recall, in a challenge-response protocol authentica-

tion is achieved by demonstrating the ability to cor-

rectly decrypt an encrypted challenge. In anonymous

authentication, the veriﬁer chooses one (ﬁxed) chal-

lenge and encrypts it with everyones public-key (of

the anonymity-set). Hence, if the prover is able to

provide the challenge bit-string to the veriﬁer, the

veriﬁer can be sure that the unknown prover is in

possession of at least one secret which corresponds

to one of the n public-keys. In protocol 1, we as-

sume that a user u

authenticates against a directory

D = ((ID

,PK

),... ,(ID

,PK

)).

However, the veriﬁer can cheat by encrypting dis-

tinct challenges c

,. .. ,c

for distinguishing differ-

ent responders based on the speciﬁc challenge. If

the encryptions of all ciphertexts in the challenge-

sequence are deterministic (such as RSA or Rabin’s

scheme), then u

may as well encrypt c

using all re-

maining public-keys to see whether or not the chal-

lenges match (Schechter et al., 1999). This is what

we call trial encryptions. The same can be done by

turning probabilistic public-key encryption schemes

into deterministic ones (see section 3.1) as proposed

in (Slamanig et al., 2009), which is no longer prone to

SECRYPT 2010 - International Conference on Security and Cryptography

134

known security ﬂaws of the aforementioned schemes

and retains the efﬁciency. Nevertheless, the compu-

tational effort for the user is linear in the size of the

anonymity-set in any case and furthermore the user

needs to be in possession of all other public-keys.

To reduce the computational effort, users could per-

form trial encryptions only for a reasonably small ran-

domly subsequence of the challenge-sequence result-

ing in more efﬁcient protocols providing probabilis-

tic anonymity (Slamanig et al., 2009). However, the

need for the public-keys of the respective users still

remains.

3.3 Postactive Anonymity

The basic idea behind postactive anonymous authen-

tication is that users do not compute trial encryptions

anymore, but post their received challenge-sequence

along with the signature for the challenge-sequence

of the veriﬁer along with the decrypted random chal-

lenge to a public bulletin-board. Clearly, this should

not be done until the user has successfully authenti-

cated and the challenge is invalidated.

Now, we assume that users help each other and

visit the bulletin-board frequently to check whether

the veriﬁer behaves honest. This can be done, when

deterministic PKE schemes (obtained by applying the

EwH construction discussed in section 3.1) are used

and the challenge (the plaintext) is known. If a user

notices that a veriﬁer has cheated, the user can show

this transcript to a judge and can convincehim that the

veriﬁer has cheated. Since the veriﬁer has digitally

signed the transcript, he cannot repudiate the cheat-

ing behavior. The veriﬁer can still cheat in this sce-

nario and thus identify a single user who authenticates

anonymously, but his trustworthiness is in jeopardy as

he is likely to be caught.

The beauty of post-active anonymity is that it

passes back the full risk to the dishonest veriﬁer: if

he attempts to discover an anonymous enquirer, then

he takes a high risk of loosing the trust of the com-

munity. Postactive anonymity therefore makes hon-

esty veriﬁer’s best behavior strategy. Furthermore,

it should be noted that this paradigm provides a su-

perior feature, namely users may register public-keys

of arbitrary cryptosystems and only the veriﬁer needs

to support all algorithms (and those users checking

entire challenge-sequences). The user solely uses

the respective algorithm corresponding to his public-

key cryptosystem and furthermore needs to compute

only one decryption operation. This results in a low

and constant computational effort, whereas all other

approaches require effort linear in the size of D ,

which can be enormous for large sets of authorized

users. However, it should be noted that the size of

the ciphertext-sequence grows linear with the size of

D , which can be quite large. In these cases, users

may randomly choose a subset D

′

⊂ D for their

anonymity-set such that the size of the ciphertext-

sequence is acceptable. For instance, if the public-

key encryption scheme of choice will be ElGamal

(ElGamal, 1984) on Elliptic Curves E(Z

), where

p is a prime with |p| = 192 bits, then, a choice of

the anonymity-set with |D

′

| = 100 will lead to a

ciphertext-sequence of ≈ 5 KB, which is reasonably

small.

4 OUR APPROACH

To realize anonymous and unlinkable but authorized

transactions, we brieﬂy review the concept of blind

signatures and provide a generic construction of a

protocol for such transactions based on one-show to-

kens from blind signatures. Thereafter, we intro-

duce our approach by combining postactive anony-

mous authentication with such one-showtokens. Sub-

sequently, we gradually augment this construction to

achieve (1) ﬁne-grained validity periods for tokens,

(2) selective traceability and (3) discuss how to pre-

vent resp. detect cloning attacks.

4.1 Blind Signatures

Blind signatures are a well known cryptographic

primitive introduced in (Chaum, 1982), which pro-

vide a means such that an entity is able to obtain a

valid signature on a message without the signer be-

ing able to learn anything about the message at the

time of signing. More precisely, the signer actually

signs a randomly blinded message and the resulting

signature can subsequently be unblinded by the orig-

inator, wheres the originator obtains a valid signature

for the original message. Consequently, the signed

message cannot be linked to the originator by the

signer. We rely our construction on efﬁcient two-

move blind signature schemes. Therefore, we can

take the RSA based scheme of (Chaum, 1982), which

was proven to be secure for the full-domain hash

RSA scheme (FDH-RSA) in the random oracle model

under the chosen-target-one-more-RSA-inversion as-

sumption (Bellare et al., 2003). Alternatively, we

can take the blind signature scheme form (Boldyreva,

2003) which is based on the BLS signature (Boneh

et al., 2004) and is provably secure in the random or-

acle model under the chosen-target Computational-

Difﬁe-Hellman assumption. Subsequently, we ab-

stract from the concrete protocol and denote the blind-

ANONYMOUS BUT AUTHORIZED TRANSACTIONS SUPPORTING SELECTIVE TRACEABILITY

135

User Service-Provider

= (t

,σ

),PK SK,BL

create

i+1

= B(H(t

i+1

))

i+1

) (t

i+1

)

/∈ BL

(H(t

),σ

)

= accept

i+1

= S

(

i+1

)

(σ

i+1

) (σ

i+1

)

i+1

= B

−1

(σ

i+1

)

i+1

= (t

i+1

,σ

i+1

)

Protocol 2: Simple Blind Signature-Based Transactions (SBSBT).

ing operation of a message m as m = B(m) and the

unblinding of the signature σ as σ = B

−1

(σ).

4.2 Anonymous Unlinkable One-show

Tokens

Below, we provide a generic protocol to obtain one-

show tokens from a veriﬁer which can be shown to

the same party (spent) in an anonymous and unlink-

able fashion. The basic idea behind this construction

was proposed in (Stubblebine et al., 1999), however,

providing non of the functionalities discussed in this

section and not combined with anonymous authenti-

cation.

We deﬁne a token as a simple data-structure which

can be described as a tuple (id

,id

), whereas id

is a unique token-ID, id

is an ID of the service-

provider and id

may represent an ID of the respective

service (the token may be augmented by further ele-

ments, e.g. validity-period, as discussed subsequently

in this section). We want to note, that what we de-

note as a token is often also referred to as a ticket,

a credential, a coupon, a transaction-pseudonym or a

one-time-pseudonym.

For now, assume that user u

holds an initial token-

signature pair t

= (t

,σ

) from the service-provider

(also denoted as the veriﬁer V, for short), e.g. the

user registers to the service-provider, pays and ob-

tains a signed token t

. Furthermore, assume that

the service-providergenerates a key-pair with suitable

parameters for issuing blind signatures, with public-

key PK

and private-key SK

. The generic proto-

col for conducting anonymous and unlinkable trans-

actions with V is illustrated in protocol 2. In order

to make the tokens one-time-usage-only, the veriﬁer

maintains a blacklist BL to blacklist already seen to-

kens and discard tokens upon seeing them again. As-

sume now that user u

wants to authorize a query

to the service-provider. In order to obtain a new

signed token for another transaction, u

computes a

blinded token t

i+1

= B(H(t

i+1

)), whereas H denotes

a suitable collision resistant cryptographic hash func-

tion and t

i+1

represents a new token. User u

sends

i+1

) to the veriﬁer, who checks whether the

token is well formed and the ID of t

is not already

contained in the blacklist. If this holds, he computes

i+1

= S

i+1

), i.e signs the blinded token, and

sends the resulting signature σ

i+1

along with the re-

sult R

of the query Q

back to u

. The user in turn

unblinds the signature and obtains σ

i+1

= B

−1

(σ

i+1

a valid signature for H(t

i+1

). Consequently, u

can use

i+1

to authorize a new transaction resp. query Q

i+1

for some data at the veriﬁer.

4.3 A Combined Approach

The idea is to combine the aforementioned approach

to realize one-show tokens with the concept of anony-

mous authentication. It should be noted that one

could use several classes of anonymous authentica-

tion schemes for this purpose, e.g. ring signatures

(Rivest et al., 2001), group signatures (Ateniese et al.,

2000), but we will assume that anonymous authenti-

cation from public-key encryption (PKE) is used. The

combination can be realized as follows:

1. Registration. Initially a user u

registers once to

the service-provider (veriﬁer) by providing iden-

tifying information ID

together with a the user’s

public-keyPK

. The veriﬁer adds the user and the

public-key to the public directory D of authorized

users.

2. Authentication. The user anonymously authenti-

cates to the veriﬁer and after a successful authen-

tication the user obtains a blind signature for a to-

SECRYPT 2010 - International Conference on Security and Cryptography

136

ken t

and thus holds a token-signature pair t

,σ

) for a subsequent transaction. Later, the

user posts the challenge-sequence along with the

signature and the challenge such that other users

can check whether the service-provider cheats.

3. Access. The user provides t

and a new blinded

token together with a query to the veriﬁer and ob-

tains a response, which is either a response to the

query and a signature on the new blinded token

for a subsequent transaction or an indication that

the transaction was not authorized.

The register procedure is carried out once for every

user. In order to obtain access to the system, a user

conducts the authentication procedure with the veri-

ﬁer. Every authentication procedure is connected to

a set of subsequent transactions, whereas the number

of sequenced transaction is not limited by the veriﬁer.

Subsequently, we will discuss how a subscription of a

user can be terminated, since this is impossible in the

aforementioned setting.

4.4 Fine-grained Validity Periods

A natural and efﬁcient approach to exclude users from

being able to conduct further transactions be realized

as follows:

• The service-provider discretizes the time into

time-periods ∆

,∆

,. .. of duration d

∆

(they may

also differ for different time-periods) and assigns

a unique random number δ

to every time-period

∆

. The most important point is, that the service-

provider solely publishes δ

for the current time-

period δ

and given all random numbers of previ-

ous and the actual time-periods it is infeasible to

compute δ

for some future time-period.

• The random number δ

needs to be included into

the token by the user, otherwise the token will

be rejected. Hence, we augment our token by an

additional element and tokens can now be repre-

sented as a tuple t = (id

,id

,δ

). Within a

time-period an authorized user can obtain an “ini-

tial” token by means of a successful anonymous

authentication.

• Service-providers can easily manage the termina-

tion of service accesses of a user by removing a

user from the directory D . It should be noted, that

the termination of service access during a time-

period is impossible, but the service-provider is

able to control the granularity by choosing ade-

quate durations of time-periods.

• Since the validity of tokens is restricted to a

speciﬁc time-period, the service-provider solely

needs to blacklist tokens within the actual period.

Due to the limited duration, the blacklist is bound

in size and previous blacklists can be discarded,

which makes the approach entirely practical from

this point of view.

4.5 Selective Traceability

Traceability in this context means, that a trusted third

party (TTP), a so called traceability authority (TA), is

able to identify the owner of a token as well as it’s

position within a sequence of transactions conducted

by a user. Besides, it is desirable to achieve selective

traceability for all tokens of the user within a speciﬁc

time-period ∆

. This means, that all tokens of a suspi-

cious user can be found, without violating the privacy

of other users. But it is important, that the service-

provider has no means to revoke the anonymity of

honest users by himself. In order to achieve this, we

require the user to register a pseudonym γ

(which

is randomly sampled from an appropriate space) with

the TA, and this pseudonym is solely known to the

TA and the user’s smart-card (and not to the service-

provider). The tamper resistant smart-card of the user

has to maintain an internal counter

cnt

, which is ini-

tialized to a ﬁxed user-speciﬁc value (which we will

discuss below) during every instance of an anony-

mous authentication protocol and incremented during

every generation of a new token.

Basically, the user’s smart-card includes addi-

tional traceability information e into the token on

behalf of the user. Hence, every token t will be

augmented by an element e and will be a tuple

t = (id

,id

,δ

,e), where e = E

(γ

cnt

;ω)

represents a probabilistic encryption of the tuple

(γ

cnt

) under TA’s public-key. Note that ω are

the random coins for the probabilistic encryption al-

gorithm, which will be discussed below. After com-

puting a token, the smart-card increments the counter

cnt

for the next token. In order to avoid partial

knowledge about the plaintext we choose user- and

time-period-speciﬁc start values of counters by com-

puting the initial value of

cnt

denoted as

cnt

init

(which is initialized during every anonymous authen-

tication) based on a suitable pseudorandom function.

Working in the random oracle model, we can use a

suitable cryptographic hash function H and compute

the initial value as

cnt

init

= H(γ

,δ

) which pro-

vides us an initial counter value that depends on the

pseudonym and on the current time-period.

4.5.1 Tracing of Single Showings

It is obvious that in case of suspicion the respective

token (which is maintained by the service-provider in

ANONYMOUS BUT AUTHORIZED TRANSACTIONS SUPPORTING SELECTIVE TRACEABILITY

137

his blacklist) can be given to the TA, which in turn

can decrypt e and obtain the pseudonym of the user.

Consequently, the identity corresponding to the user’s

pseudonym can be returned to the service-provider.

To prevent this user from being able to conduct any

future transaction, the service-provider has to remove

the respective user from his directory D used for au-

thentication. Consequently, this user will no longer be

able to conduct anonymous authentications with the

system. In this setting, the TA is very powerful, since

it can identify all users behind all transactions. How-

ever, we assume that the TA is trusted and only pro-

vides “necessary” information to the service-provider

if and only if the service-provider can credibly argue

that fraud or misuse has happened. It should be noted,

that in order to decrease the trust, we could share the

private-keyof the TA among a set of TA’s and perform

threshold-decryption to reveal the identity of a user.

4.5.2 Efﬁcient Selective Traceability

It order to protect the privacy of other (innocent) users

and to reduce the amount of workload for the TA,

we propose a novel way to achieve selective trace-

ability. Trivially, the TA could realize this feature

by decrypting all remaining tokens in the blacklist

and picking out those of the suspicious users. How-

ever, we want to protect the privacy of the remaining

users and go the other way round. Essentially, the TA

re-encrypts potential escrow information of the user

and searches the blacklist for these potential values.

How this is achieved will be discussed in the follow-

ing. The TA knows the counter value

cnt

act

and the

pseudonym of the user by decrypting the escrow in-

formation e of the suspicious token. Since the TA

also knows that the counter is incremented during the

creation of a new token and knows the value for the

current time-period δ

, it is able to compute the start-

ing value of the user as

cnt

init

= H(γ

,δ

). Conse-

quently, the TA has to look for tokens in the counter-

interval [

cnt

init

cnt

act

+ k], where k is some positive

integer. Basically, the TA looks k tokens ahead from

the start, since it cannot determine the actual number

of transaction of the suspicious user within his “ses-

sion”. The concrete choice of k mainly depends on

the application, however, when assuming that transac-

tions are distributed uniformly among users we could

take k = |BL|/|D |, where |BL| represents the arith-

metic mean of the sizes of all previous blacklists.

Now, we need a measure for the TA to actually

ﬁnd the respective tokens within the blacklist. This

can be easily achieved by converting the probabilistic

public-key encryption scheme used by the TA into a

deterministic one, i.e. by applying the EwH construc-

tion. We apply exactly this strategy to the construc-

tion of the escrow information e. More precisely, we

construct the random coins ω for the encryption algo-

rithm as ω = H(PK

,(γ

cnt

)), whereas PK

TA’s public-key. Algorithm 1 illustrates how the TA

realizes selective traceability when given a suspicious

token and the blacklist of the service-provider.

Algorithm 1: Selective Tracing.

Input: A suspicious token

t = (t,e), the value δ of

the current time-period, a parameter k, a blacklist

BL and a key-pair (PK

,SK

) of a public-keyen-

cryption algorithm.

Output: A sequence T = (

,. .. ,

) of transactions.

(γ,

cnt

act

,δ) ⇐ D

(e)

cnt

init

⇐ H(γ,δ)

pos ⇐ 0;

for all i =

cnt

init

cnt

act

+ k do

⇐ H(PK

,(γ,i))

⇐ E

(γ,i;ω

)

⇐

searchBL

,BL)

6= null then

T[pos] ⇐

pos+ +

end if

end for

return T

The algorithm

searchBL

simply searches the black-

list BL for tokens with escrow information e

. By

realizing the strategy discussed above, the workload

of the TA can be signiﬁcantly decreased. If we de-

note the size of the interval [

cnt

init

cnt

act

+ k] by m,

we achieve O(m) encryption operations over O(n) de-

cryption operations in the trivial case, since we can

assume that m ≪ n holds. Furthermore, the privacy of

innocent users does not need to be violated.

4.6 Enforcing Traceability

A very simple attack to circumvent the traceability

property is as follows. Assume that the smart-card

performs the identity-escrow on behalf of the user

and assume further that the user behaves malicious,

i.e. wants to hinder the TA to identify him in case of

fraud or misuse. Therefore, assume that a user is cur-

rently conducting transactions and obtains a response

R along with the blind signature σ

for the new token

from the service-provider in the ﬁrst step (it could,

however, also be the initial transaction). The user

passes the signature to his smart-card, which in turn

computes σ

= B

−1

(σ

), generates a new blinded to-

ken t

′

(including the traceability information e) and

passes the tuple (t, σ

′

) to the user. Although t

′

SECRYPT 2010 - International Conference on Security and Cryptography

138

is well-formed, the malicious user can easily replace

′

with another blinded token t

′′

that is nearly well-

formed. More precisely, the token is well-formed, ex-

cept for the traceability information (which could ei-

ther be chosen at random or represents the encryption

of some random value).

The conceptually most straightforward approach

to solve this problem is, that the smart-card simply

encrypts the tuple (t,σ

′

) under a service-provider’s

public-key of a secure public-key encryption scheme.

Consequently, the user will never have access to a tu-

ple of the form (t,σ

), which would allow him to con-

duct a transaction with a replaced “self-constructed”

non-traceable new blinded token t

′′

. However, the

public-key of the service-provider needs to be in-

tegrated into the smart-card in an authentic fash-

ion. Otherwise, a malicious user can easily mount a

person-in-the-middle attack by providing some arbi-

trary public-key(for whom the correspondingprivate-

key is known to the user) to the smart-card. Conse-

quently, the user can decrypt the ciphertext and obtain

a tuple (t, σ

′

) which he can modify to (t,σ

′′

) and

send this tuple encrypted under the service-provider’s

public-key.

4.7 Cloning Protection

The drawback of ﬁne-grained validity periods is,

that it is potentially susceptible to what we call the

cloning-attack. Loosely spoken, this attack means

that a fraudulent authorized users may obtain valid

token-signature pairs that he can make available to

a set of unauthorized users. These users, the so

called clones, are consequently able to anonymously

conduct a sequence of transactions with the service-

provider within the respective time-period, although

they are not authorized to do so. Note that this at-

tack is still possible when the smart-card only gives

the ciphertext of the tuple (t,σ

′

) to the user. How-

ever, the attack is somewhat reduced, since the clone

will solely be able to conduct a single transaction.

By applying counters

cnt

as discussed in section 4.6,

this attack is easy to detect. Therefore, the service-

provider only has to search for identical escrowvalues

e in his blacklist.

• If a user u

gives away his encrypted tuple

,σ

) to a clone and the clone spends the

token, the entry in the blacklist will contain

traceability information e

= E

(γ

cnt

;ω),

whereas ω = H(PK

,(γ

cnt

)) and

cnt

H(γ

,δ

• If the user authenticates again within the same

time-period, the traceability information e

′

of the

token t

′

will be identical, since the counter is

reinitialized to

cnt

= H(γ

,δ

Hence, if the service-provider detects such a cloning

attack (tokens where e

= e

for some i 6= j), he can

give both entries of the blacklist to the TA to revoke

the anonymity of the misbehaving user. It should be

noted, that this could be problematic in case of bro-

ken connections. The service-providercould have dif-

ferent strategies for handling this, whereas we brieﬂy

sketch two of them below.

Upon presenting exactly the same token multiple

times, the service-provider may re-send the response

to the query Q attached to the respective token t.

However, that incidence should be indicated by not

attaching a query, whenever re-showing a token, as

this query has been submitted anyway. Still, a request

to re-send the answer should come with the token, in

case the query did not make it through in the ﬁrst in-

stance. However, if neither is done, and a known to-

ken t with a new (different to the previous) query Q

′

(6= Q) is coming in, then the veriﬁer should become

wary and start tracing. This ensures robustness of the

protocol as well it creates a simple mechanism to de-

tect piracy

Alternatively, the service-provider could realize

some kind of glitch-tolerance, by deﬁning some

threshold K of “clone-activity”, which need to be

reached before revoking users.

5 SECURITY ANALYSIS

In this section we will discuss the threat model and

investigate the security of the proposed construction.

Therefore, we assume that users communicate their

messages to service-providers over a communication

channel that provides perfect anonymity and unlinka-

bility of exchanged messages, as it is the case with all

interactive protocols providing such features.

5.1 Threat Model

We assume that the manufacturer of the smart-cards

is trustworthy and hence the smart-cards are tamper

resistant and do not contain any backdoors, Trojan

horses, etc. Furthermore, users are assumed to be

dishonest (active adversaries), i.e. will actively try

to fool the service-provider resp. authorize unautho-

rized users, which is a reasonable assumption for real-

world scenarios. Service-providers are honest-but-

curious, i.e. follow the protocol speciﬁcation but use

any gathered information in order to try to identify

anonymous users. However, service-providers can

ANONYMOUS BUT AUTHORIZED TRANSACTIONS SUPPORTING SELECTIVE TRACEABILITY

139

also be active adversaries, but only with respect to the

anonymous authentication protocol.

5.2 Anonymous Authentication

For the used anonymous authentication protocol we

require anonymity, correctness, unforgeability and

unlinkability, which can be proven to hold for exist-

ing protocols (Slamanig et al., 2009; Lindell, 2007).

However, the known deﬁnitions of anonymity and un-

linkability are less formally ensured in the post-active

anonymity setting. Clearly, anonymity can be bro-

ken if the veriﬁer encrypts distinct random challenges,

which consequently can restore linkability too. How-

ever, it is equally obvious that a cheating veriﬁer acts

completely on his own risk, as the community will

accuse him of being dishonest. In that case, the ser-

vice will not be used any more, and a cheating veri-

ﬁer could loose more than he could win. The correct-

ness and unforgeability properties are retained, since

solely trial encryptions are omitted. Finally, it should

be noted that when using standard anonymousauthen-

tication (Schechter et al., 1999; Slamanig et al., 2009;

Lindell, 2007), we obtain security with respect to

existing deﬁnitions, however, at substantially higher

costs.

5.3 Security of our Construction

In our investigation of the security of the construc-

tion we investigate the anonymity of transactions, the

unlinkability of transactions and the unforgeability of

tokens. We inspect every property below and sketch

the ideas:

• Transaction Anonymity. Every token showing

integrates the issuing of a new token. Hence, we

ﬁrstly need to look at the token which is shown

and secondly the blinded token which is signed

by the veriﬁer. The anonymity of the token t

shown reduces to inspecting the escrow informa-

tion e. The anonymity follows from two ob-

servations concerning the escrow information e.

Firstly, (Bellare et al., 2007) prove that for any at

least IND-CPA secure probabilistic public-key en-

cryption that is converted into a deterministic one

(by applying the EwH construction), it holds that

an adversary provided with encryptions of plain-

texts drawn from a message-space of high min-

entropy (which is clearly the case, since we en-

crypt randomly chosen pseudonyms along with

a value obtained by evaluating a pseudorandom

function on this value) will have negligible ad-

vantage in computing any public-key independent

partial information function of the plaintexts (this

notion is called PRIV in (Bellare et al., 2007)).

Hence, the so obtained deterministic public-key

encryption scheme provides the required security

guarantees and can be seen as a computationally

hiding commitment. Secondly, the pseudonyms

of users are sampled at random from a large

enough space and are solely known to the TA and

the user’s smart-cards (which are assumed to be

tamper-proof). Consequently, any adversary can

solely guess the respective pseudonym of a user,

which would allow him to identify or trace one

user. By choosing the space for the pseudonyms

accordingly large, this probability can be made

negligible. The anonymity of the blinded token

follows from the properties of the blind signature

scheme.

• Unforgeability. Since the smart-card solely gives

ciphertexts of tuples (t,σ

′

) to the users, a user

would need to forge a signature from the veri-

ﬁer. However, this means that a user would need

to existentially forge a signature for the signature

scheme underlying the blind signature scheme.

• Unlinkability. The unlinkability of the issuing

and showing of a token t reduces to the blind-

ness property of the used blind signature scheme.

Hence, there is no way for the signer to relate

the issuing and showing of a token. Furthermore,

we need to look at the unlinkability of different

showings, which means that it cannot be decided

whether a set tokens was shown by the same user.

Therefore, our argumentation is similar to that

used for the transaction anonymity property. Let

us assume without loss of generality that we have

two tokens t and t

′

. Only e and e

′

contain infor-

mation about the user. However, as already dis-

cussed in context of transaction anonymity e and

′

are computationally hiding commitments.

6 FUTURE ASPECTS

One drawback of the approach presented in this paper

is that we cannot realize a ﬁne-grained access con-

trol for resources connected to services. However,

this can be solved by using partially blind signatures

(Abe and Fujisaki, 1996; Abe and Okamoto, 2000)

instead of blind signatures. Loosely spoken, in a par-

tially blind signature scheme, a receiver blinds a mes-

sage m, obtains m = B(m) and sends m to the signer.

The signer computes a partially blind signature σ =

(m,info), which includes a common information

info and sends σ to the receiver. The receiver unblinds

σ by computing σ = B

−1

(σ), can verify whether the

SECRYPT 2010 - International Conference on Security and Cryptography

140

common information info was included and obtains a

valid signature σ for the tuple (m, info). Note, that the

message m is entirely unknown to the signer. We can

use them as follows: The service-provider deﬁnes the

set of privileges P (which are connected to resources

of services) and during registration privileges are as-

signed to users. By choosing the anonymity-set ac-

cording to required privileges (users which have the

same privileges) an encoding of these privileges can

be integrated by means of common information info

into the blinded token. Hence, when presenting the to-

ken, the service-provider can decide whether a query

Q will be authorized or not. It should be noted, that

anonymity and unlinkability are preserved.

REFERENCES

Abe, M. and Fujisaki, E. (1996). How to Date Blind Sig-

natures. In ASIACRYPT ’96, volume 1163 of LNCS,

pages 244–251. Springer.

Abe, M. and Okamoto, T. (2000). Provably Secure Partially

Blind Signatures. In CRYPTO ’00, volume 1880 of

LNCS, pages 271–286. Springer.

Ateniese, G., Camenisch, J., Joye, M., and Tsudik, G.

(2000). A Practical and Provably Secure Coalition-

Resistant Group Signature Scheme. In CRYPTO ’00,

volume 1880 of LNCS, pages 255–270. Springer.

Bellare, M., Boldyreva, A., and O’Neill, A. (2007). De-

terministic and Efﬁciently Searchable Encryption. In

CRYPTO 2007, volume 4622 of LNCS, pages 535–

552. Springer.

Bellare, M., Namprempre, C., Pointcheval, D., and Se-

manko, M. (2003). The One-More-RSA-Inversion

Problems and the Security of Chaum’s Blind Signa-

ture Scheme. J. Cryptology, 16(3):185–215.

Blanton, M. (2008). Online Subscriptions with Anonymous

Access. In ASIACCS 2008, pages 217–227. ACM.

Boldyreva, A. (2003). Threshold Signatures, Multisigna-

tures and Blind Signatures Based on the Gap-Difﬁe-

Hellman-Group Signature Scheme. In PKC 2003, vol-

ume 2567 of LNCS, pages 31–46. Springer.

Boneh, D., Lynn, B., and Shacham, H. (2004). Short Sig-

natures from the Weil Pairing. Journal of Cryptology,

17(4):297–319.

Camenisch, J., Hohenberger, S., Kohlweiss, M., Lysyan-

skaya, A., and Meyerovich, M. (2006). How to Win

the Clone Wars: Efﬁcient Periodic n-Times Anony-

mous Authentication. In CCS ’06, pages 201–210.

ACM.

Camenisch, J. and Lysyanskaya, A. (2001). An Efﬁcient

System for Non-transferable Anonymous Credentials

with Optional Anonymity Revocation. In EURO-

CRYPT ’01, volume 2045 of LNCS, pages 93–118.

Springer.

Camenisch, J. and Lysyanskaya, A. (2002). A Signature

Scheme with Efﬁcient Protocols. In SCN’ 02, volume

2576 of LNCS, pages 268–289. Springer.

Camenisch, J. and Lysyanskaya, A. (2004). Signature

Schemes and Anonymous Credentials from Bilinear

Maps. In CRYPTO 2004, volume 3152 of LNCS,

pages 56–72. Springer.

Canard, S., Gouget, A., and Hufschmitt, E. (2006). A

Handy Multi-coupon System. In ACNS 2006, volume

3989 of LNCS, pages 66–81. Springer.

Chaum, D. (1982). Blind Signatures for Untraceable Pay-

ments. In CRYPTO’82, pages 199–203. Plemum

Press.

Chaum, D. (1985). Security without identiﬁcation: Trans-

action systems to make big brother obsolete. Com-

mun. ACM, 28(10):1030–1044.

Chen, L., Escalante, A. N., L¨ohr, H., Manulis, M., and

Sadeghi, A.-R. (2007). A Privacy-Protecting Multi-

Coupon Scheme with Stronger Protection Against

Splitting. In FC 2007, volume 4886 of LNCS, pages

29–44. Springer.

ElGamal, T. (1984). A Public Key Cryptosystem and a

Signature Scheme Based on Discrete Logarithms. In

CRYPTO ’84, volume 196 of LNCS, pages 10–18.

Springer.

Kiayias, A., Tsiounis, Y., and Yung, M. (2004). Trace-

able Signatures. In EUROCRYPT ’04, volume 3027

of LNCS, pages 571–589. Springer.

Libert, B. and Yung, M. (2009). Efﬁcient Traceable Signa-

tures in the Standard Model. In Pairing 2009, volume

5671 of LNCS, pages 187–205. Springer.

Lindell, Y. (2007). Anonymous Authentication - Preserving

Your Privacy Online. Black Hat 2007.

Lysyanskaya, A., Rivest, R. L., Sahai, A., and Wolf, S.

(2000). Pseudonym Systems. In SAC ’00, volume

1758 of LNCS, pages 184–199. Springer.

Rivest, R. L., Shamir, A., and Tauman, Y. (2001). How to

Leak a Secret. In ASIACRYPT ’01, volume 2248 of

LNCS, pages 552–565. Springer.

Schechter, S., Parnell, T., and Hartemink, A. (1999).

Anonymous Authentication of Membership in Dy-

namic Groups. In FC 1999, volume 1648 of LNCS,

pages 184–195. Springer.

Slamanig, D., Schartner, P., and Stingl, C. (2009). Practi-

cal Traceable Anonymous Identiﬁcation. In SECRYPT

2009, pages 225–232. INSTICC Press.

Stubblebine, S. G., Syverson, P. F., and Goldschlag, D. M.

(1999). Unlinkable Serial Transactions: Protocols and

Applications. ACM Trans. Inf. Syst. Secur., 2(4):354–

389.

Verheul, E. R. (2001). Self-Blindable Credential Certiﬁ-

cates from the Weil Pairing. In ASIACRYPT ’01, vol-

ume 2248 of LNCS, pages 533–551. Springer.

Xi, Y., Sha, K., Shi, W., Schwiebert, L., and Zhang, T.

(2008). Probabilistic Adaptive Anonymous Authen-

tication in Vehicular Networks. J. Comput. Sci. Tech-

nol., 23(6):916–928.

ANONYMOUS BUT AUTHORIZED TRANSACTIONS SUPPORTING SELECTIVE TRACEABILITY

141