HTEE: AN HMAC BASED TAMPER EVIDENT ENCRYPTION

Bradley Baker and C. Edward Chow†

Department of Computer Science, University of Colorado at Colorado Springs

1420 Austin Bluffs Parkway, Colorado Springs, CO 80918, U.S.A.

Keywords: Encryption, Integrity, Confidentiality, HMAC, Tamper Detection, Hash.

Abstract: This paper presents a HMAC based Temper Evident Encryption (HTEE) technique for providing

confidentiality and integrity of numeric data in a database environment through an encryption scheme based

on the keyed Hash Message Authentication Code (HMAC) function. The encryption scheme implemented

in this project extends and improves an existing HMAC based encryption scheme. The result is a symmetric

encryption process which detects unauthorized updates to ciphertext data, verifies integrity and provides

confidentiality. This encryption scheme provides an alternative to standard approaches that offer

confidentiality and integrity of data such as combining the Advanced Encryption Standard (AES) algorithm

with a hash digest. The purpose of the scheme is to provide a straightforward and efficient encryption that

supports data integrity, to investigate the use of HMAC for reversible encryption and key transformation,

and to improve upon an existing method.

1 INTRODUCTION

Databases are used to store a wide variety of

sensitive data ranging from personally identifiable

information to financial records and other critical

applications. The volume and importance of

sensitive data stored and processed electronically is

constantly growing, and this data must be protected

from unauthorized disclosure or modification.

Confidentiality and integrity of this sensitive data

must be maintained for legal or fiscal reasons

(Pavlou and Snodgrass, 2008), (Kher and Kim,

2005). Due to the wide range of problem domains, a

variety of solutions are of interest to suit particular

situations (Sivathanu et al., 2005).

This paper provides confidentiality and tamper

detection in a database environment. Existing work

supports tamper detection and integrity for database

systems using techniques such as access control,

auditing and other methods. Additional related work

includes forensic analysis of database tampering

(Pavlou and Snodgrass, 2008). Some techniques

apply encryption and authentication in parallel to

provide confidentiality and integrity (Torres et al.,

2006a), (Torres et al., 2006b). Unlike these

techniques, this paper uses an encryption scheme

based on the keyed Hash Message Authentication

Code (HMAC) (Bellare et al., 1996) (NIST, 2002)

for confidentiality and integrity. Existing work uses

HMAC for integrity but it is not typically used for

confidentiality. An exception is presented by Lee et

al. (2007), which investigates HMAC as an

encryption function.

The encryption scheme used for this paper offers

tamper detection and confidentiality directly in the

encrypted data field rather than externally or at the

system level. Cryptography provides standard

algorithms that also support confidentiality and

integrity in the encrypted data field, including

symmetric and asymmetric encryption algorithms

for confidentiality and hash digest or signature

algorithms for integrity. Combining these solutions

can require detailed processing by the end user and

may not be ideal for all problem domains.

1.1 Project Overview

In a database record sensitive data is paired with

information that uniquely identifies the record such

as primary key or hash digest. Each row in a

database table contains a combination of uniquely

identifying information and sensitive data, and this

relationship must be preserved from encryption

through decryption. The relationship can be

†: This research work was supported in part by two NISSSC AFOS

grant awards under numbers FA9550-06-1-0477 and FA9550-04-1-

0239.

196

Baker B. and Edward Chow C. (2010).

HTEE: AN HMAC BASED TAMPER EVIDENT ENCRYPTION.

In Proceedings of the International Conference on Security and Cryptography, pages 196-205

DOI: 10.5220/0002997301960205

 SciTePress

tampered with while data is encrypted, when this

occurs the integrity of the data is lost.

Typically encryption algorithms such as the

Advanced Encryption Standard (AES) provide

confidentiality but don’t provide integrity and hash

digest algorithms such as Secure Hash Algorithm

(SHA) provide integrity without confidentiality

(Forouzan, 2008). Traditional methods to obtain

both confidentiality and integrity involve combining

encryption and digest algorithms. Message

authentication codes such as HMAC provide an

alternative to traditional hash digests where the

digest is protected from unauthorized update with a

secret key.

This paper presents a HMAC based encryption

scheme that provides confidentiality and tamper

detection for positive integer data. This scheme is an

improvement in efficiency and tamper detection to

the HMAC integer encryption concept presented in

(Lee et al. 2007). The scheme is implemented in the

PostgreSQL database environment (PostgreSQL,

2009), and the developed process is named “HMAC

based Tamper Evident Encryption”, referred to as

HTEE in this paper. This process is simpler to use

than the standard AES with SHA solution, and more

efficient for encryption. However this process is

slower on decryption than AES with SHA, and the

security of this scheme is dependent on the security

of the underlying hash function.

The HTEE scheme is a symmetric encryption

process that relies on a secret key and processes

positive integer values. The integer plaintext values

are decomposed into components, or buckets, using

modulus arithmetic. The buckets have a fixed size of

1,000, so integer values are decomposed into the

value of the ones, thousands, millions, etc. places.

The plaintext buckets are encrypted using the

HMAC function, where the hash digest represents

the ciphertext. The secret key is modified for each

plaintext value and each bucket value using a

specific transformation process resulting in a

different key for every HMAC operation. The key

transformation process is based on a unique value

related to the sensitive data, such as a database

primary key. A primary goal of the HTEE process is

the detection of unauthorized updates or tampering

with ciphertext data, particularly when ciphertext

values are interchanged. The key transformation

process ensures ciphertext values can’t be changed

without detection.

The decryption process is similar to the

encryption process and uses the same key

transformation sequence. Because the HMAC

function produces a one-way hash digest, it is not

trivial to reverse the operation. In order to find the

correct plaintext for each bucket’s digest value a

search is performed across all 1,000 possible bucket

values, calculating the HMAC digest of each until a

match is found. The search is repeated for all

buckets and the modulus decomposition is reversed

to obtain the plaintext value. Any unauthorized

updates to ciphertext data are detected in the

decryption step by a failure to find a matching

HMAC digest.

2 BACKGROUND

2.1 Hash Message Authentication Code

HMAC is a symmetric process that uses a secret key

and a hash algorithm such as SHA to generate a

message authentication code, or digest. This

authentication code securely provides data integrity

and authenticity because the secret key is required to

reproduce the code. Digests for normal hash

functions can be reproduced with no such constraint.

HMAC can protect against man-in-the-middle

attacks on the message, but it is not designed to

encrypt the message itself. The HMAC function was

published by Bellare et al. (1996), which includes

analysis and a proof of the function’s security, and it

is standardized in FIPS PUB 198 (NIST, 2002). Any

hash algorithm can be used with HMAC including

MD5, SHA-1, SHA-256, etc.

The output of HMAC is a binary authentication

code equal in length to the hash function digest. The

security of HMAC is directly related to the

underlying hash function used, so it is weaker with

MD5 and stronger with SHA-512. Forgery and key

recovery attacks threaten HMAC, but typically

require a large number of message/digest pairs for

analysis. The HMAC functions used in the

implementation of the HTEE scheme are based on

the SHA-1 hash algorithm. The use of HMAC-

SHA1 specifies some data sizes that are important in

the HTEE implementation such as a 64 byte key size

20 byte digest output size.

2.2 HMAC Integer Encryption

The HTEE algorithm is based on an original HMAC

encryption scheme presented by Lee et al. (2007),

and provides several improvements. A detailed

analysis and discussion of this original scheme is

available in (Baker, 2009a). The original scheme

uses integer decomposition, HMAC for encryption,

and decryption with exhaustive search. Because the

HTEE: AN HMAC BASED TAMPER EVIDENT ENCRYPTION

197

original scheme does not combine related data with

the plaintext data it cannot be used for tamper

detection.

The original encryption scheme takes a positive

integer input as plaintext, and computes the

remainder of the plaintext and a predefined bucket

size. After calculating the remainder a bucket ID is

found as the quotient of division between plaintext

and bucket size.

Encryption uses a secret key, a seed value, the

plaintext bucket ID and the remainder. The

encrypted bucket ID is found by calculating the

HMAC function recursively N times, where N is

equal to the bucket ID. On the first iteration, the

secret key and a predefined seed value are input into

HMAC. For successive iterations, the output of the

previous HMAC is used as input into the next

iteration with the secret key. The bucket ID is not

directly encrypted, but the execution of recursive

HMAC is based on the value of the bucket ID.

The encrypted value for the remainder is found

in a similar operation differing only in the secret

key. When encrypting the remainder value the

corresponding bucket ID is appended to the

beginning of the secret key to form a new key. The

recursive HMAC operation is the same using the

new key. Beginning with the seed, the digest is

calculated N times where N is equal to the value of

the remainder.

Decryption uses an inverse transformation that

must search through potential bucket ID and

remainder values. The maximum bucket ID must be

defined to constrain the search process. The first step

for the decryption transformation is finding the

bucket ID of the ciphertext data. The same seed and

key value from encryption are used in the HMAC

operation, and this operation is executed N times for

the number of possible buckets. Each HMAC digest

is compared against the encrypted bucket ID for a

match. If a match is found, the bucket ID plaintext is

equal to the number of iterations executed.

A similar search is made for the remainder value

using a new key constructed by appending the

decrypted bucket ID to the beginning of the secret

key. Once the plaintext bucket ID and remainder

values are known, the modulus decomposition is

reversed to generate the original plaintext from the

decrypted bucket ID and remainder.

Issues identified with the original scheme

include the problem that two buckets decrease

efficiency for large integer values, the key

transformation only occurs on the remainder value

rather than the bucket ID, and the highly recursive

use of HMAC is inefficient (Baker, 2009a).

3 DESIGN

The HTEE process is similar to the original HMAC

encryption scheme in that positive integer values are

processed, these values are decomposed into

components, also called buckets, and the bucket

values are processed through HMAC for encryption.

The combination of HMAC output for all bucket

values creates the ciphertext. The decryption step

calculates the HMAC digest for all possible bucket

values, where a match between calculated digest and

ciphertext data indicates the correct plaintext result.

HTEE uses multiple smaller buckets to reduce

decryption search ranges, and it adds a key

transformation process that ensures each bucket of

each plaintext uses a different encryption key. The

key transformation process ensures tamper

detection.

3.1 Plaintext Decomposition

The first step of the encryption process is

decomposition of the integer plaintext input. In the

HTEE scheme, the integer plaintext value is

decomposed into multiple buckets of size 1,000 to

improve search efficiency. The number of buckets

used for a given plaintext is calculated with:

floor(log

1000

(Plaintext)) + 1 (1)

Because each bucket produces one HMAC digest

value, larger plaintext values will produce a larger

ciphertext. In order to avoid leaking information

about the plaintext’s order of magnitude, a domain

specific maximum number of buckets are defined

and small plaintext values are padded. Using more

buckets of smaller sizes allows the decryption

operation to be more efficient because a smaller

number of HMAC searches must be performed.

Additional improvements to performance can be

achieved if fewer buckets are needed in a problem

domain, such as storing nine digit values versus

sixteen digit values.

3.2 Key Transformation

The second step of the encryption process is key

transformation, which prepares distinct secret keys

for the encryption of each bucket value. The HTEE

scheme improves the original process and adds

tamper detection by defining two key transformation

functions, an element transformation and a bucket

transformation. The element key transformation

creates a new secret key for each plaintext value

SECRYPT 2010 - International Conference on Security and Cryptography

198

processed. This transformation is seeded with

information relating the plaintext data to its

environment, providing tamper detection. The

bucket key transformation produces a new secret key

used on each decomposed bucket value of a given

plaintext. The bucket key is the effective encryption

key because only decomposed bucket values are

encrypted. The method of key transformation used

for bucket values also contributes to tamper

detection because it is a continuation of the element

key process. Both the bucket and element

transformations use the HMAC function to generate

new secret key data. For its use here as a key

transformation function, HMAC is considered a

pseudo-random value generator. Research supports

HMAC as a pseudo-random function, as discussed

in (Bellare et al. 1996), (Bellare 2006), (Canetti

2007), (Kim et al. 2006). The key transformation

functions used for HTEE provide a critical security

feature that makes analysis of the ciphertext output

more difficult.

3.3 Element Key Transformation

The HTEE scheme transforms the element key based

on a unique value. This process constructs an

element key using the original secret key and

uniquely identifiable data related to the plaintext

value. Usually the unique value is the primary key of

the database record, but any data unique to the

plaintext can be used. The hash digest of the unique

value is found with the SHA-1 algorithm, and used

as input into the HMAC function alongside the

original secret key. The output of this HMAC

operation is used for the first 20 bytes of the element

key, and it is used as input into another HMAC

operation with the original secret key. The output of

the second operation is used for the second 20 bytes

of the element key, and it is processed through

HMAC again. This process repeats until four

recursive HMAC operations are executed, outputting

80 bytes of key data. The output is then truncated to

64 bytes, producing the element key. This process is

depicted graphically in Figure 1.

An attacker cannot reproduce the key if given the

unique value, because the process is secured with the

HMAC function and secret key. The key

transformation process is important for HTEE

tamper detection because it incorporates information

related to the plaintext value with the encryption of

the value. The result is that decryption of the

ciphertext is dependent on the unique value, and any

changes between ciphertext and unique value can be

detected.

Figure 1: Element key transformation.

3.4 Bucket Key Transform

The second key transformation function used by

HTEE is the bucket key transformation. The HTEE

process uses a different key for each bucket’s

HMAC function so that buckets with equal values

do not have equal digests. The bucket key

transformation is iterative, and 20 bytes of the

bucket key are replaced for each bucket processed in

a plaintext. The first bucket key is equal to the

element key generated for the plaintext value. Each

succeeding bucket key is generated by processing

the bucket’s HMAC encryption ciphertext through

HMAC again with the original secret key. The result

of this HMAC operation is appended to the

beginning of the bucket key, and the result is

truncated to 64 bytes resulting in the succeeding

bucket key.

The bucket key transformation is summarized

graphically in Figure 2. The function presented in

Figure 2 depicts both the calculation of the bucket

ciphertext as well as the transformation of the bucket

key. The bucket key transformation makes

encryption keys dependent on both the unique value

used to generate the element key, and the order of

processing for the bucket values. The combination

of element and bucket key transformations produces

distinct keys for each plaintext bucket value

provided that differing unique values are input.

HTEE: AN HMAC BASED TAMPER EVIDENT ENCRYPTION

199

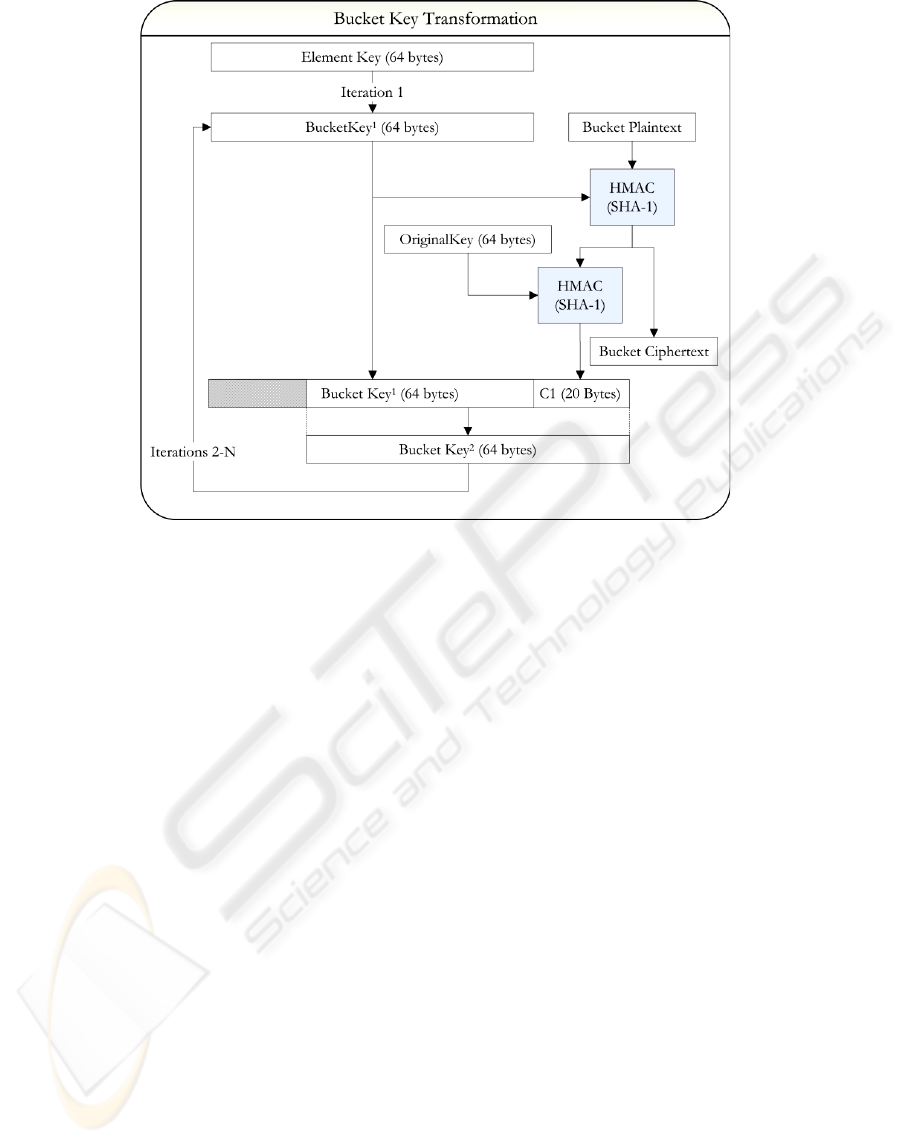
Figure 2: Bucket key transformation and encryption.

The only cases when the key generation process will

not result in distinct keys are for hash collisions of

the unique value data, which are extremely rare

cases.

3.5 Encryption

The encryption step of the process calculates the

HMAC digest using the key and plaintext values for

each bucket. The digests are concatenated to form

the ciphertext output.

The HTEE encryption operation is a very

efficient process regarding computation time,

because the HMAC function is executed a small

number of times. For example, when processing a

plaintext value using four buckets, HMAC will be

invoked twelve times. However, the decryption

process for HTEE presents a performance challenge

due to the need for exhaustive searching across

possible plaintext values. In the example of a four

bucket plaintext, HMAC could be executed up to

4,008 times.

3.6 Decryption

The HTEE decryption operation is similar to the

encryption operation, particularly with the key

transformation functions. The same progression of

element keys and bucket keys is calculated, except

these keys are used for a search across all plaintext

bucket values. The first step in the decryption

process is splitting the concatenated ciphertext string

into individual bucket digests. Then the key

transformation process is used with the unique value

data (which cannot be encrypted) to find the same

bucket key values used during encryption. The

process then iterates through all possible bucket

plaintext values, 0 through 999, calculating the

HMAC digest for each one with the bucket key. The

intermediate digest is compared with the stored

bucket digest, if the values match then the current

iteration is the bucket’s plaintext value. If no records

from 0 through 999 match the bucket digest, then

some corruption or tampering of the ciphertext has

occurred. This step is the critical tamper detection

operation for HMAC; the absence of a correct

decryption match indicates that the ciphertext data or

unique value has changed since encryption. Once all

bucket plaintext values are identified, the modulus

decomposition is reversed.

4 ANALYSIS

4.1 HMAC Security

The security of the HTEE scheme is primarily based

on the security of the HMAC function, because

SECRYPT 2010 - International Conference on Security and Cryptography

200

HMAC is used for both key transformation and

encryption. Existing work has established that the

security or cryptographic strength of the HMAC

function is directly related to the security of the

underlying hash function on which is it based

(Bellare et al. 1996), (Bellare 2005), (Bellare 2006).

Although recent findings on collision attacks have

invalidated the use of the MD5 hash algorithm and

decreased confidence in the SHA-1 algorithm, these

attacks have limited impact on HMAC security.

HMAC is proven to be secure provided that the hash

compression operation is a pseudo-random function

(Bellare 2006), (Contini et al. 2006 ). In addition the

secret key reduces the effect of collision based

attacks on the HMAC function (Bellare 2005),

(Bellare 2006), (Kim et al. 2006).

While the strength of HMAC security is based

on the compression operation of the underlying hash

function, the measure of security is the difficulty to

produce a forgery of the authentication code. There

are several methods researched to produce forgeries

in the HMAC function, the primary being the

birthday attack. Although collisions of the

underlying hash function are not a concern for the

HMAC, it is still the case the HMAC output is a

digest of a message and secret key input, and it can

produce its own collisions. It is possible for an

attacker to observe two different messages that have

the same digest output. The probability of this

occurrence is controlled by the birthday paradox,

where a HMAC collision becomes probable after 2

n/2

message pairs are observed, where n is the number

of bits in the output digest (Bellare 2005 ), (Kim et

al. 2006). A HMAC-SHA1 function would be

susceptible to a forgery based on the birthday

paradox after 2

message pairs are observed. When

attacking HMAC with the birthday paradox, the

attacker relies on a legitimate user to generate all 2

digests. Also the effect of a birthday attack is a

forgery, and does not yield the secret key so impact

is limited.

Full key recovery attacks are another threat to

the HMAC function. These attacks still appear

infeasible, although some methods have efficiency

improvements (Fouque et al. 2007), (Contini et al.

2006), (Sasaki 2009). These methods have an

underlying requirement of a very large number of

HMAC message/authentication code pairs for

analysis, more than are required for the birthday

attack.

4.2 HTEE Security

In the context of the HTEE scheme, the HMAC

operation is secure considering typical birthday and

key recovery attacks. In an environment with 2

records and six buckets of HMAC digest data for

each record, this is not close enough to the number

of messages required to perform key retrieval or

birthday attacks if HMAC-SHA1 is used (Bellare et

al. 1996), (Fouque et al. 2007), (Contini et al. 2006).

An additional consideration for security of the

HTEE scheme includes the input of unique value

and plaintext value as messages for the HMAC

function. The data ranges for unique value can vary

widely according to the problem domain, and the

plaintext value will always have a small range due to

the HTEE bucket decomposition limiting values to

integers (0-999). The key transformation process

provides a layer of protection for small values

because any analysis of the ciphertext data will be

challenged with constantly varying keys. However,

the key transformation process begins with the

unique value input which is known to the attacker

since it cannot be encrypted in the database. A likely

method for an attacker to pursue is attacking the key

transformation function using the unencrypted

unique values. The natural variation of the unique

value is masked by the hash and recursive HMAC

functions in the element key transformation.

Considering the use of HMAC as a pseudo-

random function, the variation in key values through

the transformation process should be unpredictable.

This is expected even if the unique value size is

small, due to the pseudo-random feature of the

underlying hash compression function. Additional

data could be provided for the unique related value,

thus expanding it beyond the range of small input

values.

The structure of the HTEE scheme provides

additional protection by obscuring internal values in

a similar way to the inner and outer hash operations

of the HMAC function. Consider that the attacker

knows two values: the ciphertext output from HTEE,

and the unique value input. The HTEE function can

be written in a short format as:

HTEE(P,K,U) = HMAC(P, f

(K,U)) (2)

Where P is the plaintext value, K is the original

secret key, U is the unique value, and f

is the key

transformation function. The f

function is a

combination of several HMAC steps as described

previously, and produces intermediate keys. It is

difficult for the attacker to generate the intermediate

key used with a plaintext value, based on the

HTEE: AN HMAC BASED TAMPER EVIDENT ENCRYPTION

201

analysis of HMAC key recovery attacks. It is also

difficult for the attacker to identify the secret key

using the unique input message because the result of

function f

is not known.

4.3 HTEE Tamper Detection

Tamper detection is an important feature of the

HTEE scheme and can be defined as the failure in

data integrity between the ciphertext and the

remainder of the database record. The data integrity

relationship can be defined at a minimum as the

record’s primary key and the plaintext/ciphertext

value.

An attacker can try to modify the data record in

three ways: Case 1) Make a random change to

ciphertext, Case 2) Interchange two ciphertext

values and Case 3) Make a change to the unique

value. The tamper detection feature of HTEE will

detect each of these changes through the decryption

viability test. If the modifications in Cases 1 or 2

were used, the unique value would be unchanged

and the key transformation sequence for decryption

would be identical to the encryption operation. Each

step in the decryption search would iterate through

possible plaintext values, but none of the HMAC

digests would match the stored value. The

probability of a false positive would be extremely

small, approximately 3.42 x 10

-43

, based on the

birthday attack with 1,000 values (Forouzan 2008).

This result is obtained with the formula:

P = 1 – e

(

)

(3)

Where k is the sample size, equal to 1,000 and N

is the number of possible values, equal to 2

160

for

SHA-1. If the modification in Case 3 was used, the

key transformation sequence would be changed

resulting in a similarly improbable collision. The

new key transformation and a value between (0-999)

would have to collide with the original transformed

key and a value between (0-999).

5 IMPLEMENTATION

The HTEE scheme was implemented to validate the

designed algorithm, evaluate performance, and

provide a tool that could be used for future

applications. The implementation is an add-on for

the PostgreSQL database management system and

provides encryption and tamper detection features.

The implementation uses the HMAC operation

with SHA-1 as underlying hash function and for the

element key transformation. The use of HMAC-

SHA1 specifies several parameter sizes that are

important during implementation including the key

size of 64 bytes and the digest size as a multiple of

20 bytes per bucket. The bucket size used for the

implementation is 1,000, which breaks numbers into

buckets by order of magnitude such as millions,

billions, etc.

Each bucket value is up to three plaintext digits

(values 0-999) which are encrypted into 28 base64

encoded characters. A six bucket HTEE ciphertext

would require 168 bytes of text data. This is a nine-

fold increase in storage space when the plaintext is

stored as a text string. However, the equivalent AES

ciphertext requires 116 bytes of base64 text data in

PostgreSQL, so HTEE is only a 44% increase over

the AES requirement. The large increase in storage

space is one of the costs of using the more efficient

small bucket solution employed by HTEE. The other

primary cost is decryption processing time.

5.1 Testing Summary

Several tests were performed on HTEE including

comparisons to AES based techniques. Three

encryption techniques were tested in a PostgreSQL

database system: 1) Raw AES encryption, 2) AES

encryption with unique value data and 3) the HTEE

encryption scheme. Method 1, the raw AES

encryption scheme, is straightforward and uses AES

with a secret key value. This method can detect

random changes to ciphertext data, but it cannot

detect other tampering. Method 2, using AES

encryption with unique value data is a solution that

adds tamper detection to the raw AES encryption.

The approach used for AES tamper detection

includes concatenating the unique value data with

the plaintext data, and encrypting the combined

string. On decryption, the unique value is separated

from the plaintext, and the plaintext is recovered. If

the decrypted unique value differs from the current

unique value, the data was tampered with. The

HTEE encryption scheme used the primary key as

unique value and managed tamper detection

internally.

The testing process used six datasets, each

composed of 20,000 randomly generated integers.

The datasets were each configured with a different

number of buckets, so one dataset had values

between 0 and 999 (one bucket), another dataset had

values between 1,000 and 999,000 (two buckets),

etc. up to the six buckets or 18 digits. Performance

was timed for the encryption, decryption and tamper

detection operations. The tamper detection dataset

SECRYPT 2010 - International Conference on Security and Cryptography

202

was built by interchanging half of the ciphertext

records.

5.2 Testing Results

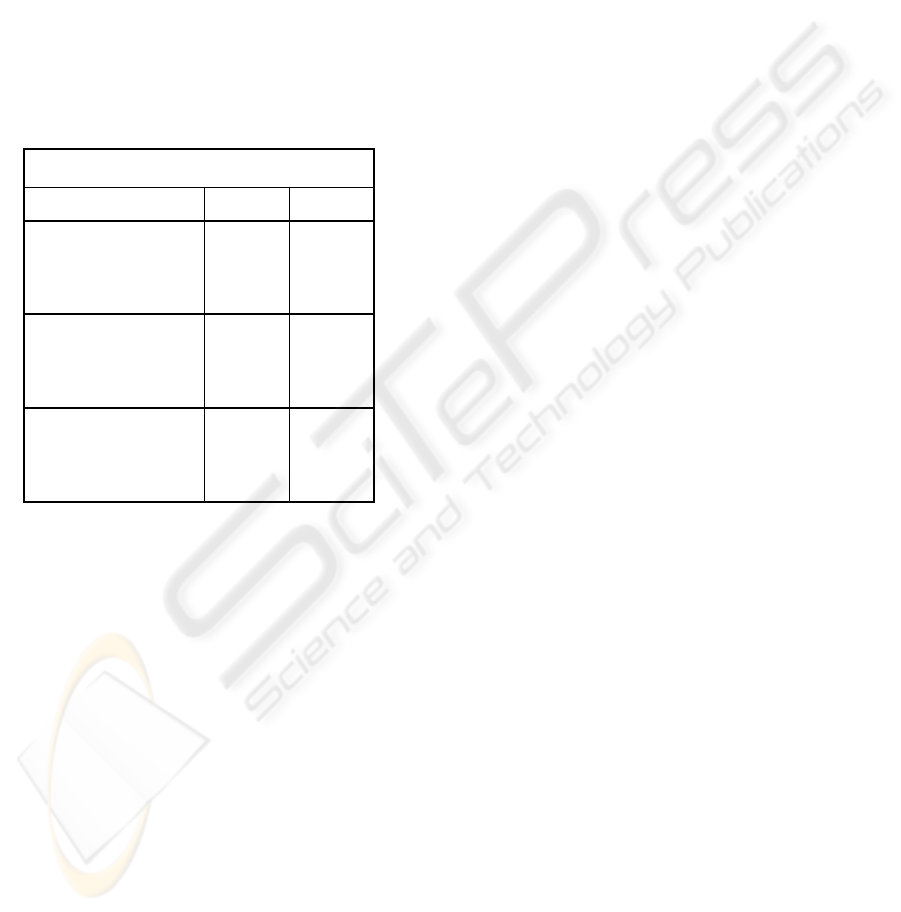
Performance results from testing are summarized in

Table 1. The average performance times

demonstrate the trade-off in efficiency between the

HTEE scheme and AES based schemes. The

encryption operation for AES with tamper detection

was about 4.5 times slower than the encryption

operation for HTEE. Conversely, the decryption

operation for HTEE was about 4.1 times slower than

the decryption operation for AES.

Table 1: Average performance across bucket sizes.

Average Performance

(time in seconds)

Encrypt Method Mode Time

Original AES encrypt 18.1

Original AES decrypt 15.3

Original AES tamper 18.3

Tamper Detect AES encrypt 15.8

Tamper Detect AES decrypt 18.2

Tamper Detect AES tamper 17.8

HTEE encrypt 3.5

HTEE decrypt 75.4

HTEE tamper 58.8

Performance of HTEE varies according to the

bucket size used. The number of buckets processed

affected HTEE encryption marginally, but more

buckets decreased performance of decryption and

tamper detection greatly. This was due to the

exhaustive search required for decryption, where

processing time increases with number of buckets.

Efficiency improved for tampered datasets because

the process could identify the tampering early in

processing. The AES methods provide consistent

performance for encryption and decryption - near

seventeen seconds for each run regardless of bucket

size. The HTEE scheme provides consistent fast

performance for encryption at less than five seconds

per run, but the processing time for decryption

increases to over two minutes depending on the

number of buckets processed.

5.3 Performance Analysis

The performance results from testing indicate a four-

fold decrease in encryption time and four-fold

increase in decryption time over AES. This would be

a reasonable trade-off for some encryption heavy

domains. The HTEE scheme also shows a

performance improvement over the original HMAC

encryption scheme (Lee et al. 2007) based on the

algorithmic structure of the methods. The

performance of the two schemes is generalized

based on the number of HMAC operations required

for encryption and decryption. The complexity of

the HTEE algorithm can be summarized as

approximately:

2*log

1000

(n) (4)

1001*log

1000

(n) (5)

Where (4) is the encryption complexity because

of the encryption and key transformation HMAC

functions, and (5) is the decryption complexity for

the exhaustive search and key transformation.

These performance expectations are compared

against the original HMAC encryption scheme.

Based on the analysis of the original scheme

presented in (Baker, 2009a), the encryption and

decryption operations are equal in efficiency if

processing a single plaintext value. For large

numbers the complexity can be summarized as

approximately:

2*n

0.5

(6)

For both encryption and decryption because of

the larger bucket sizes, ideally set to the square root

of the maximum plaintext value. HTEE has a

constant relative complexity, and the original

scheme has polynomial performance.

Performance testing verifies the improvement in

processing time with the HTEE scheme over the

original HMAC encryption method. As presented in

(Baker, 2009a), a test of the original scheme with

2,000 integer values took 2 minutes and decryption

took 3 minutes. These results are much slower than

the HTEE performance times seen with all of the

20,000 integer datasets, represented by the average

in Table 1.

6 CONCLUSIONS

The HTEE scheme provides a framework for tamper

detection and encryption of integers in a database

environment that can be useful in some applications.

Benefits to the approach include the simplicity of a

single-column confidentiality and integrity solution,

trustworthy tamper detection based on a hash

function, and efficient encryption speed. Drawbacks

HTEE: AN HMAC BASED TAMPER EVIDENT ENCRYPTION

203

to the approach include inefficient decryption and

increased volume of ciphertext.

The security analysis shows that the

cryptographic strength of HTEE is based on the

HMAC function and in turn the underlying hash

function, SHA-1. Recent work suggests that HMAC

is not affected by collision attacks against SHA-1

(Bellare, 2005). (Bellare, 2006). Key recovery

attacks are a threat to the HTEE scheme but these

are still considered infeasible, and require a very

large number of valid HMAC authentication codes

(Fouque et al. 2007), (Contini et al. 2006 ). Until a

complete mathematical proof is generated, HTEE is

considered not as secure as the AES encryption

standard, and applications bound by regulatory

requirements should continue to use AES methods.

The HTEE scheme is distinguished by plaintext

decomposition into multiple buckets and secret key

transformation functions. The multiple bucket

solution makes decryption feasible for large integers,

and key transformation functions increase security

through layering and provide tamper detection

through unique related values. The scheme can

detect changes between a stored ciphertext value and

other data related to it such as a record’s primary

key or hash digest value. The tamper detection

feature is only provided on decryption, in order to be

alerted to database tampering, the records must be

decrypted.

The performance of the HTEE scheme is faster

on encryption than AES, but slower on decryption.

The differences are a factor of four in each case. For

large numbers, the HTEE scheme is several orders

of magnitude faster than the HMAC based

encryption scheme it is based on. The HTEE scheme

produces 44% more ciphertext data than an

equivalent AES encryption scheme.

Applications for the HTEE scheme include areas

where integer data is used, fast encryption speed is

desired, slow decryption speed is not a significant

concern, and tamper detection is needed. An

example of this would be auditing systems or the

archival of financial transactions. In these cases, a

large number of records can be created on a daily

basis, but the records might be infrequently

referenced in the future. The HTEE method can

support regular insertions into archive tables as

opposed to a block encryption method that would

require re-encryption of the entire data column. In a

database that is write-only, or has little read access

of encrypted records, HTEE can provide efficient

tamper evident encryption as a supplementary

protection for the database system. The full paper

and project materials are presented in (Baker,

2009b).

6.1 Future Work

Some opportunities for future work related to the

HTEE scheme include support for expanded

plaintext values and a rigorous security proof. The

HTEE scheme improved the original HMAC

encryption concept to make encryption of larger

integers (up to 9x10

) feasible. However, the

scheme is still limited to positive integer values

because there is no way to encode negative or

floating point values. A future improvement to the

method could be a mechanism to process negative

numbers, floating point numbers, and potentially

ASCII-encoded text data.

This paper presented a conceptual argument for

HTEE security based on existing work for HMAC

security and key recovery. Based on the designed

structure of HTEE, this provides a reasonable

assurance of cryptographic strength because HMAC

is the underlying function used, and it is widely

considered to be a secure process. The security of

HTEE is based on the HMAC function as a pseudo-

random generator, both for key transformation and

encryption. Future work can present a proof of the

security for HTEE, which should focus on the

random-generation capability of HMAC with the

unique values used in the key transformation

process.

REFERENCES

Brad Baker, 2009a "Analysis of an HMAC Based

Database Encryption Scheme," UCCS Summer 2009

Independent study July. 2009

URL: http://cs.uccs.edu/~gsc/pub/master/bbaker/doc/

final_paper_bbaker_cs592.doc

Brad Baker, 2009b “Tamper Evident Encryption of

Integers using keyed Hash Message Authentication

Code” Project materials and documentation. December

2009 URL = http://cs.uccs.edu/~gsc/pub/master/

bbaker/

Forouzan, Behrouz A. 2008. Cryptography and Network

Security. McGraw Hill higher Education. ISBN 978-0-

07-287022-0

Mihir Bellare; Ran Canetti; Hugo Krawczyk; “Keying

Hash Functions for Message Authentication”, IACR

Crypto 1996 URL: http://cseweb.ucsd.edu/

users/mihir/papers/kmd5.pdf

Mihir Bellare, “Attacks on SHA-1,” 2005 URL:

http://www.openauthentication.org/pdfs/Attacks%20o

n%20SHA-1.pdf

SECRYPT 2010 - International Conference on Security and Cryptography

204

Mihir Bellare, “New Proofs for NMAC and HMAC:

Security without Collision-Resistance,” IACR Crypto

2006. URL: http://eprint.iacr.org/2006/043.pdf

Ran Canetti, “The HMAC construction: A decade later,”

2007. URL: http://people.csail.mit.edu/canetti/

materials/hmac-10.pdf

Scott Contini; Yiqun Lisa Yin, “Forgery and Partial Key-

Recovery Attacks on HMAC and NMAC using Hash

Collisions (Extended Version),” 2006 URI: http://

eprint.iacr.org/2006/319.pdf

Pierre-Alain Fouque; Gaëtan Leurent; Phong Q. Nguyen,

"Full Key-Recovery Attacks on HMAC/NMAC-MD4

and NMAC-MD5," IACR Crypto 2007

URL: ftp://ftp.di.ens.fr/pub/users/pnguyen/Crypto07.

pdf

Vishal Kher; Yongdae Kim, “Securing Distributed

Storage: Challenges, Techniques, and Systems”

Workshop On Storage Security And Survivability,

Nov. 2005 URL = http://doi.acm.org/10.1145/

1103780.1103783

Jongsung Kim; Alex Biryukov; Bart Preneel; and Seokhie

Hong, “On the Security of HMAC and NMAC Based

on HAVAL, MD4, MD5, SHA-0 and SHA-1”, 2006.

URL: http://eprint.iacr.org/2006/187.pdf

Dong Hyeok Lee; You Jin Song; Sung Min Lee; Taek

Yong Nam; Jong Su Jang, 2007 "How to Construct a

New Encryption Scheme Supporting Range Queries

on Encrypted Database," Convergence Information

Technology, 2007. International Conference on , vol.,

no., pp.1402-1407, 21-23 Nov. 2007. URL: http://

ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=44204

52&isnumber=4420217

NIST, March 2002. FIPS Pub 198 HMAC specification.

URL = http://csrc.nist.gov/publications/fips/fips198/

fips-198a.pdf

Kyriacos Pavlou; Richard Snodgrass, “Forensic Analysis

of Database Tampering,” ACM Transactions on

Database Systems (TODS), 2008. URL = http://

doi.acm.org/10.1145/1412331.1412342

PostgreSQL, October 2009. Server Documentation. URL=

http://www.postgresql.org/docs/8.4/static/index.html

Yu Sasaki, “A Full Key Recovery Attack on HMAC-

AURORA-512,” 2009 URL: http://eprint.iacr.org/

2009/125.pdf

Gopalan Sivathanu; Charles P. Wright; and Erez Zadok,

“Ensuring data integrity in storage: techniques and

applications,” Workshop On Storage Security And

Survivability, Nov. 2005 URL = http://doi.acm.org/

10.1145/1103780.1103784

Torres et al. 2006a

Elbaz, R.; Torres, L.; Sassatelli, G.; Guillemin, P.;

Bardouillet, M.; Rigaud, J.B., 2006a "How to Add the

Integrity Checking Capability to Block Encryption

Algorithms," Research in Microelectronics and

Electronics 2006, Ph. D. , vol., no., pp.369-372, 0-0 0

URI: http://ieeexplore.ieee.org/stamp/stamp.jsp?

arnumber=1689972&isnumber=35631

Torres et al. 2006b

Elbaz, R.; Torres, L.; Sassatelli, G.; Guillemin, P.;

Bardouillet, M., 2006b "PE-ICE: Parallelized

Encryption and Integrity Checking Engine," Design

and Diagnostics of Electronic Circuits and systems,

2006 IEEE, vol., no., pp.141-142, 0-0 0. URL: http://

ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=16495

95&isnumber=34591

HTEE: AN HMAC BASED TAMPER EVIDENT ENCRYPTION

205