
SEARCHING OPTIMAL SIGMA PARAMETER IN RADIAL
BASIS KERNEL SUPPORT VECTOR MACHINE FOR
CLASSIFICATION OF HIV SUB-TYPE VIRUSES
Zeyneb Kurt
Department of Computer Engineering, Yildiz Technical University, Yildiz, Istanbul, Turkey
Oguzhan Yavuz
Department of Electronics and Communications Engineering, Yildiz Technical University, Yildiz, Istanbul, Turkey
Keywords: Auto-regressive Model, HIV, Support Vector Machine, ROC Analysis.
Abstract: We propose intelligent methods to classify two different HIV virus types, i.e., R5X4 and R5 or X4 with low
computational complexity. Since R5X5 virus has same the features of R5 and X4 viruses, diagnosis of
R5X4 can not be determined easily. In this study, the statistical data of R5X4, R5 and X4 was obtained by
accessible residues and modelled by Auto-regressive (AR) model. After that the pre-processed data was
used for determining the optimal
value in Radial Basis Kernel of Support Vector Machine (SVM).
1 INTRODUCTION
In this work, the statistical data of R5X4, R5 and X4
HIV viruses was obtained by accessible residues and
modeled by Auto-Regressive (AR) model for
reducing dimension. Hereafter, SVM structures were
evolved to determine R5X4 viruses successfully by
using the pre-processed data.
In Bioinformatics, the several models have been
evolved by using gene sequences to determine HIV
sub-type viruses (Berger 1999). By using those
models, mostly the artificial neural network (ANN)
structures, which have high ability to classify, were
developed (Resch 2001, Wang 2003, Brumme 2004,
Milich 1993).
Lamers et. al. had used HIV-Base software to
obtain the data of R5X4, R5 and X4 viruses. By
using this data, ANNs had been evolved to classify
these viruses. However they had given the training
accuracy of ANNs as the classification results.
Obviously, the results could not show the real
performance of the ANNs. The data should be
separated two different datasets as training and
testing. Then the test data, which is not used in the
training process, should be used for determining the
real performance of ANNs (Lamers 2008).
The accessible residues of gene sequences had
been obtained to describe protein identity by Zhou
(Zhou 2006), whereas Kong et. al. had analyzed
accessible residues of HIV-1 genome to design
peptide (Kong 2005).
Many bioinformatics researchers have used AR
model to process gene data for spectral analyses of
short tandem in DNA sequences or for determining
period-3 behaviors (Akhtar 2007). G. Rosen had
reduced the dimension of gene sequence using AR
model (Rosen 2007).
In this work, HIV sequences were converted into
numeric data by using accessible residues. Since the
dimension of gene sequences was large and different
from each other, their dimensions were reduced and
equalized by AR model. This pre-processed data
was used for training and testing the SVM.
This paper consists of 4 sections. In Section 2,
data sets, AR model, SVM and ROC analysis are
described. In Section 3, the use of SVM in the
proposed scheme is described. The simulation
results are also given in this section. In the final
section, conclusion and future work are mentioned.
2 MATERIALS AND METHODS
In this section, we describe dataset and quantifying
163
Kurt Z. and Yavuz O. (2010).
SEARCHING OPTIMAL SIGMA PARAMETER IN RADIAL BASIS KERNEL SUPPORT VECTOR MACHINE FOR CLASSIFICATION OF HIV SUB-TYPE
VIRUSES.
In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 163-166
DOI: 10.5220/0002998101630166
Copyright
c
SciTePress

method. AR model is applied to dataset. SVM is
employed in classification process. The performance
of SVM is analyzed by ROC analysis.
2.1 Data Mining
77 R5 sequences, 31 R5X4 and 40 X4 sequences
(Lamers 2008) were downloaded from Los Alamos
National Laboratory HIV Sequence Database
(www.hiv.lanl.gov/content/hiv-db/main page.html).
These sequences were converted to numeric data
by using accessible residues. Since size of gene
sequences is different from each other, SVM could
not be applied to this dataset. That can be remedied
by AR model.
2.2 AR Model
AR model was chosen to model the gene data, since
that model represents energy of signals successfully
which is defined by all pole filters as follows:
1
()
1
M
k
k
k
G
Hz
az
(1)
where M is the dimension of AR model. Eq. 1 could
be written in time domain as,
1
M
kikik
i
x
ax w
(2)
where
k
x is the estimated signal,
i
a is the AR
coefficient,
k
w is the computational error, and M is
the number of AR coefficients (Haykin 2002).
In this work, 10-th AR model is applied to
dataset for reducing and equalizing size of sequence
due to their size is large and different from each
other. We tried to minimize M by maximizing the
classification accuracy. We have shown that if M is
chosen as 10, the performance of the algorithm is
satisfactory. As M increases, the computational
complexity of the classification scheme also
increases.
2.3 Evolving SVM
Numeric data of HIV sequences were obtained and
modeled by 10-th AR model to reduce size of HIV
sequences. In the next step, this pre-processed
dataset was used for training and testing SVM with
various sigma values to classify R5X4, R5 and X4.
SVM is a learning method introduced by V.
Vapnik (Vapnik 1999). The objective of SVM can
also be justified by structural risk minimization: the
empirical risk (training error), plus a term related
to the generalization ability of the classifier, is
minimized. In other words, the SVM loss function is
analogous to ridge regression.
Let m-dimensional inputs x
i
(i=1...m) belongs to
two classes y Є {-1,1}. The aim is finding the best
decision boundary hyperplane f(x) that maximizes
the sum of distances to the closest positive and
negative training examples. This hyperplane intents
to classify, not only train vectors but also the test
samples successfully. The hyperplane f(x) is defined
by the following transformation where k is kernel
function and b is bias value.
1
,
M
ii i
i
f
xykxxb
(3)
Kernel function can be linear as in Eq. 4, polynomial
as in Eq. 5 and radial basis as in Eq. 6.
,,
ii
kxx xx
(4)
(, ) (, )
d
ii
kxx xx
(5)
2
,exp
2
i
i
x
x
kxx
(6)
The sign of f(x) shows the class membership of x. x
i
with nonzero α
i
values are called support vectors of
the hyperplane.
2.4 ROC Analysis
Receiver Operating Characteristic Analysis (ROC
Analysis) is related in a direct and natural way to
cost/benefit analysis of diagnostic decision making.
It is originated from signal detection theory, as a
model of how well a receiver is able to detect a
signal in the presence of noise. Its key feature is the
distinction between hit rate (or true positive rate)
and false alarm rate (or false positive rate) as two
separate performance measures. ROC analysis has
also widely been used in medical data analysis to
study the effect of varying the threshold on the
numerical outcome of a diagnostic test (Kohavi
1995).
The limitations of diagnostic accuracy as a
measure of decision performance require
introduction of the concepts of the "sensitivity" and
"specificity" of a diagnostic test as shown in Table 1.
SIGMAP 2010 - International Conference on Signal Processing and Multimedia Applications
164
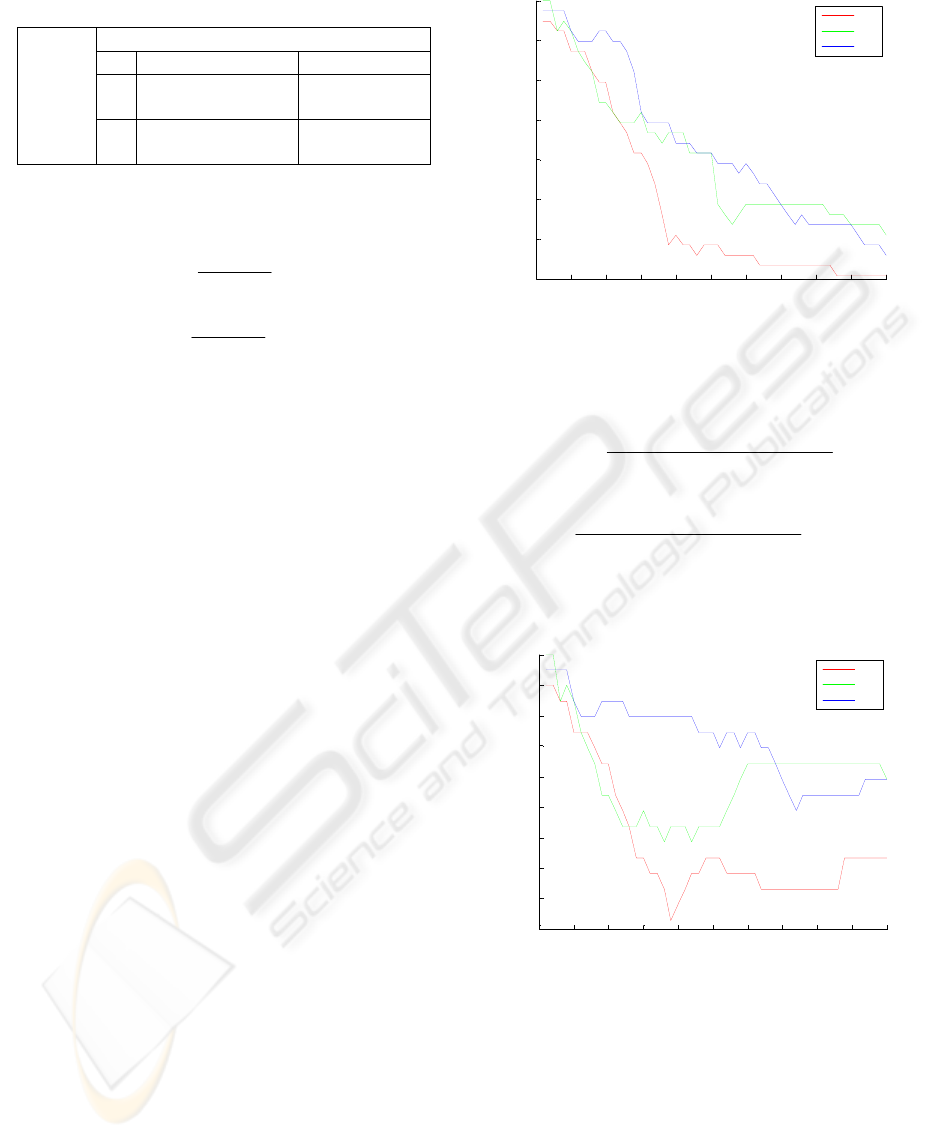
Table 1: ROC Block Diagram.
Predicte
d
Actual
T F
T True Positives (TP) False Positives
(FP)
F False Negatives (FN) True Negatives
(TN)
The sensitivity and specificity can be written as
follows:
FN
T
P
TP
ySensitivit
(7)
FP
T
N
TN
Specifity
(8)
3 EXPERIMENTAL RESULTS
SVM structure had 10-inputs and one-output. Radial
basis kernel function was used to determine the
optimal classification accuracy. The parameter
in
radial basis function was assigned 0.1; incremented
by 0.1; until 5.
The desired outputs of R5X4 and other genes
(R5 or X4) were chosen as -1 and 1 respectively.
In this study, an 3-fold cross validation was used.
There were 117 R5 or X4 samples and 31 R5X4
samples in the dataset. Due to one of the classes had
much more instances than other, instances of less
crowded class were cloned. Thus, both classes had
117 samples. Each class of HIV gene was
partitioned into three pieces which consists of 39 R5
or X4 data and 39 R5X4 data respectively. One of
the dataset was used for testing SVM, while the
remaining was used for training. The training and
test sets consisted of 156 and 78 data, respectively.
The results were given for 3-fold CV dataset which
are called CV1, CV2 and CV3.
The classification accuracy of test step according
to the parameter
was shown in Fig. 1.
The best result was obtained as 100% when the
parameter
was 0.1 for CV2. However, the
general sight of Fig. 1 illustrates that the best results
were obtained for CV3. Besides, while the parameter
was increasing, the classification accuracy was
decreasing for all datasets.
However, the classification accuracy is not
enough to analyze the performance of SVM.
Therefore, ROC analysis was applied to these
results.
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
65
70
75
80
85
90
95
100
Sigma values of RBF Kernel
Accuracy Level (%)
CV1
CV2
CV3
Figure 1: The classification accuracy of SVM.
In this study, "sensitivity" and "specificity" of
SVM could be defined as follows:
54
54 5 or 4
True
True
False
RX
Sensitivity
RX R X
(9)
5 or 4
5 or 4 5 4
True
False
True
RX
Specifiy
RX RX
(10)
Sensitivity and specificity are given Figs 2 and 3,
respectively.
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
0.55
0.6
0.65
0.7
0.75
0.8
0.85
0.9
0.95
1
Sigma values of RBF Kernel
Sensitivity Value
CV1
CV2
CV3
Figure 2: The sensitivity values of SVM
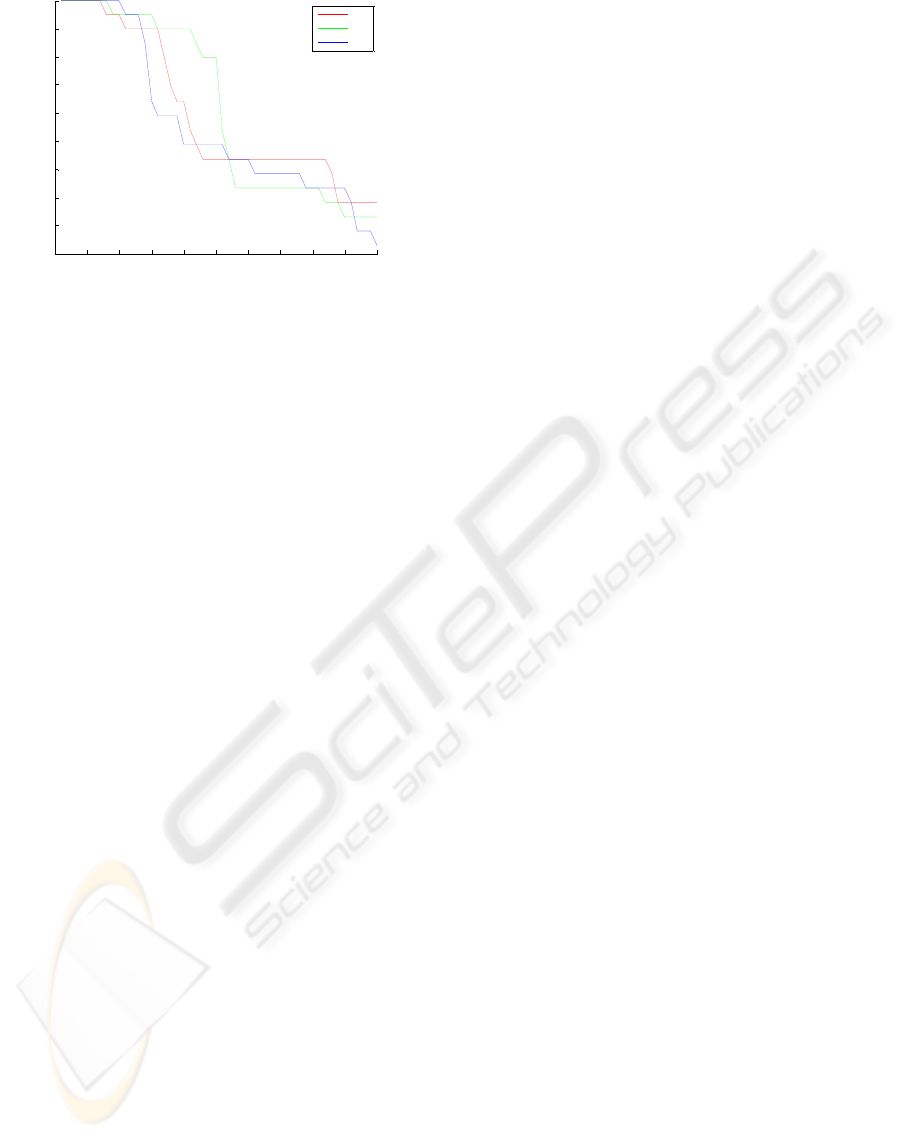
The best results of sensitivity for all datasets
were acquired while the parameter
was 0.1.
Beside, according to Fig. 2, the worst sensitivity
values were obtained while
was 1.9 for CV1, 1.8
for CV2 and 3.7 for CV3. Moreover, the minimum
specificity values were acquired when
was larger
than 4.4 for all datasets.
SEARCHING OPTIMAL SIGMA PARAMETER IN RADIAL BASIS KERNEL SUPPORT VECTOR MACHINE FOR
CLASSIFICATION OF HIV SUB-TYPE VIRUSES
165
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
0.55
0.6
0.65
0.7
0.75
0.8
0.85
0.9
0.95
1
Sigma values of RBF Kernel
Specificity Value
CV1
CV2
CV3
Figure 3: The specificity values of SVM.
4 CONCLUSIONS
In this study, the statistical data of HIV subtype
genes were obtained by accessible residues and
modeled by AR model to reduce the size of HIV
sequences. The SVM structure was used to classify
HIV sub-type viruses successfully. Thus, the
optimal parameter
in radial basis kernel of SVM
was searched by using the pre-processed data.
The training and test dataset were obtained by
using 3-fold cross-validation and these datasets were
used for training and testing the SVM.
The best classification accuracy was obtained
while the parameter
was 0.1 for all CVs.
Moreover, as the parameter
was increasing, the
accuracy levels were decreasing.
Since the classification accuracy is not enough to
analyze the performance of SVM, ROC analysis was
applied to these results. The sensitivity and
specificity were obtained as 1, when the parameter
was 0.1 for all CVs.
In future work, SVM structure and an
incremental Multilayer Perceptron implementation
will be compared and the results will be discussed.
REFERENCES
Berger, E. A., Murphy, P. M., and Farber, J. M. (1999)
Chemokine Receptors as HIV-1 Coreceptors: Roles in
Viral Entry, Tropism, and Disease. Ann. Rev.
Immunology. 17, 675-700.
Resch, W., Hoffman, N., and Swanstrom, R. (2001).
Improved Success of Phenotype Prediction of the
Human Immunodeficiency Virus Type 1 from
Envelope Variable Loop 3 Sequence Using Neural
Networks. Journal of Virology. 76, 3852-3864.
Wang, D., and Larder, B. (2003). Enhanced Prediction of
Lopinavir Resistance from Genotype by Use of
Artificial Neural Networks. J. Infectious Diseases.
188, 653-660.
Brumme, Z. L., Dong, W. W. Y., Yip, B., Wynhoven, B.,
Hoffman, N. G., Swanstrom, R., Jensen, M. A.,
Mullins, J. I., Hogg, R. S., Montaner, J. S. G., and
Harrigan, P. R. (2004). Clinical and Immunological
Impact of HIV Envelope V3 Sequence Variation after
Starting Initial Triple Antiretroviral Therapy. AIDS.
18, F1-F9.
Milich, L., Margolin, B., and Swanstrom, R. (1993). V3
Loop of the Human Immunodeficiency Virus Type 1
Env Protein: Interpreting Sequence Variability. J.
Virology. 67(9), 5623-5634.
Lamers, S., Susanna, L., Salemi, M., McGrath, M. S., and
Fogel, G. B. (2008). Prediction of R5, X4, and R5X4
HIV-1 Coreceptor Usage with Evolved Neural
Networks. Trans. On 1HComputational Biology and
Bioinformatics. 5, 291-300.
Zhou, H., and Yan, H. (2006). Autoregressive Models for
Spectral Analysis of Short Tandem Repeats in DNA
Sequences. IEEE Int. Conf. on Systems, Man and
Cybernetics. 2, 1286-1290.
Kong, R., Wang, C. X., Ma, X. H., Liu, J. H., and Chen,
W. Z. (2005). Peptides Design Based on the Interfacial
Helix of Integrase Dimer. 27th Annual Int. Conf. of the
Engineering in Medicine and Biology Society. 4743-
4746.
Akhtar, M., Ambikairajah, E., and Epps, J. (2007).
Detection of period-3 behavior in genomic sequences
using singular value decomposition. Proc. of
International Conference on Emerging Technologies.
13-17.
Rosen, G. (2007). Comparison of Autoregressive
Measures for DNA Sequence Similarity. IEEE
Genomic Signal Processing and Statistics Workshop
(GENSIPS). 13-17.
Haykin, S. (2002). Adaptive Filter Theory, New Jersey:
Prentice-Hall.
Kohavi, R. (1995). A study of cross-validation and
bootstrap for accuracy estimation and model selection.
Proceedings of the Fourteenth International Joint
Conference on Artificial Intelligence. 2, 1137–1143.
Vapnik, V. N. (1999). An overview of statistical learning
theory. IEEE Transactions on Neural Networks. 10(5),
988-999.
SIGMAP 2010 - International Conference on Signal Processing and Multimedia Applications
166
