CAWP

A Combinatorial Auction Web Platform

İbrahim Cereci and Hürevren Kılıç

Computer Engineering Department, Atılım University, İncek, Ankara, Turkey

Keywords: Online Auctions, Combinatorial Auctions, e-Commerce, Winner Determination Problem.

Abstract: Online auctions, including online Combinatorial Auctions, are important examples of e-commerce

applications. In this paper, a Combinatorial Auction Web Platform (CAWP) is introduced. The platform

enables both product selling and buying capabilities that can be realized in a combinatorial way. CAWP

supports a Sealed-Bid Single-Unit type of Combinatorial Auctions. Easy customization for any selected

problem domain is a distinguished feature of CAWP. Platform users are not expected to have any technical

knowledge about how to solve the Winner Determination Problem (WDP) known to be critical for profit

maximization of the auctioneers in Combinatorial Auctions.

1 INTRODUCTION

Auction is a trading process where auctioneer

provides goods or services and buyer bids to these

goods or services. At the end, the highest bidder

wins. Online auctions are the auctions which are

held over the internet. Rapid growth of internet

makes online auctioning important, as it reduces the

time and space cost of the offline auctioning

mechanisms. Combinatorial Auctions (CA) are the

auctions that bidders place bids on combinations of

items rather than a single item (Vries and Vohra,

2010). CAs are commonly used in application areas

like transportation (Kwon et.al., 2005), bus routes,

airport landing rights, power exchanges, carbon

permits, and radio spectrum for wireless

communications services (Milgrom, 2000) For

example, in 2002, Nigeria sold regional fixed

wireless access licenses on a sealed-bid

combinatorial auction (Koboldt et.al., 2003).

Similarly, allocation of web services via CAs is

possible. The requirement of more than one web

services to be elaborated at the same time implies a

form of bidding that supports web services

combinations (Lin et.al., 2008). CAs also used in

Supply Chain Formation. The supply chain

formation demands difficult coordination issues for

distributed negotiation of the protocols to be solved.

Parties must negotiate for multi level production

relationships with important interdependencies

among inputs and outputs of each level. CAs

addresses this problem by global optimization over

expressed offers to engage in compound exchanges

(Walsh et.al., 2000).

In practice, CAs are popular because they give

bidders a capability to express their complete

preferences. Especially, if the items in the auction

are complementary, set of items may be valued as

more than the sum of values for each individual

item. At the same time, the auctioneer may obtain

higher benefit by initiating a CA instance. This is

because of allowing bidders to express their

preferences in combinatorial way, which may results

in better auction revenues (Cramton et.al., 2007).

Automation of the CA is clearly important, because

sellers may want to maximize their revenues and let

their bidders flexibly express their preferences while

bidding for the items in the auction over the internet.

One of the main problems for the auctioneer in

an online CA is to decide about which bid(s) will be

allocated (or chosen as the winner(s)). CA allows

bidder to bid bundles of items in an auction while

these bundles may overlap. The aim is to find a

subset of all given bids that will maximize the

resulting revenue of the seller. In literature, this

problem is called as Winner Determination Problem

(WDP) known to be NP-complete (Gottlob and

Greco, 2007). Online CAs cannot perform well for

the unbounded large scale problems. But with giving

limitation to maximum number of items in an

auction, problem size can be reduced to a solvable

instances. To the best of author’s knowledge, there

Cereci Ä

r. and Kılıç H. (2010).

CAWP - A Combinatorial Auction Web Platform.

In Proceedings of the International Conference on e-Business, pages 82-88

DOI: 10.5220/0002998200820088

 SciTePress

is no CA platform realizing Consumer to Consumer

(C2C) auctions. In this paper, an online configurable

Combinatorial Auction Web Platform (CAWP) is

introduced (Cereci, 2009). The platform can be used

by consumers who want to sell or buy goods in a

combinatorial way. Basically, the consumers are not

required to know the details about how to solve the

WDP. CAWP is developed by using open source

tools and technologies. It is operating system

independent. The sellers and buyers can interact

with the system through a simple web browser

without any additional program installation.

The rest of the paper has the following

organization. In Section 2, a background information

about general auctions and their automation are

provided. In Section 3, combinatorial auctions and

the winner determination problem are explained.

Also, two alternative solutions to WDP are

discussed. In Section 4, technical details,

performance results and an example usage of CAWP

are given. The last section includes the conclusion

and future works.

2 ONLINE AUCTIONS

Emergence of the Internet has changed the way

people buy and sell goods. New types of electronic

marketplaces have been developed to create more

efficient markets (Bakos, 1998). Online Auctions

have been one of the most successful electronic

markets (Wolfram|Alpha, 2009). Success of the

online auctions comes from the capabilities that they

provide both to buyers and sellers. As a buyer, one

can bid on large number of items from different

sources and he/she has the potential to find goods in

lower prices. As a seller, you can reach great number

of potential buyers.

2.1 Auctions

There are four common auction types. Most of the

other auction types are derived from these basic four

auction types (Klemperer, 2004).

1. First-Price Sealed Bid Auction: All bidders

submit their valuations in sealed bids,

simultaneously. By this way it is guaranteed that

no bidder knows the bid of the others. The

highest bidder who pays the price gets the good.

2. English Auction (a.k.a. open-cry ascending price

auction): English auction is the most common

form of auction used today. In this form, bidders

bid openly against each other. Each bid should

be higher than the previous one. The auction

ends when no bidder is willing to raise the final

bid or bidding period is over. The highest bidder

gets the good.

3. Dutch Auction (a.k.a. open-cry descending price

auction): This auction type is similar to the

English auction. The auctioneer begins with

setting a high price to the good. Initial price is

gradually lowered until one bidder accepts to pay

that amount. Last announced amount is paid by

the bidder.

4. Vickrey Auction (a.k.a. sealed-bid second-price

auction): It is identical to the first-price sealed-

bid auction except that winning bidder pays not

his bid amount but the second highest bidder’s

amount.

2.2 Electronic Auctions

Electronic auctions became an important part of the

electronic trading. In general, complete trading

process of any online auction has the following steps

(Kumar and Feldman, 1998):

1. Initial buyer and seller registration: All parties

are authenticated.

2. Setting up a particular auction event: Goods are

described; auction rules are set and auction is

started.

3. Scheduling and advertising: Upcoming auctions

are notified to attract potential buyers.

4. Bidding: All the bids are collected. Bid validity

is verified during bidding period and bids are

placed until the bidding period is over.

5. Evaluation of bids, closing the auction: The

auction closing rules are applied and the winner

bids are determined. Winners and losers are

notified back.

6. Trade settlement: Payment and good delivery are

realized.

Furthermore, for the sake of standardization, every

electronic auction platform are also expected to

support the following properties (Omote, 2002):

1. Anonymity: Loser bidders should not be

identifiable.

2. Non-cancelability: A winner is always identified

that he cannot deny having bid to the auction.

3. Public verifiability: Anybody could publicly

verify the winning bid is really the highest value

and valid.

4. Unforgeability: Impersonation of sellers and

bidders should be prevented.

5. Robustness: Auction process should not be

interrupted, even due to invalid bids.

CAWP - A Combinatorial Auction Web Platform

6. Fairness: Every bid should have the same

priority; there should be no favor to any

individual’s bids.

7. Efficiency of bidding: The computation of

determining a winner bid and verifying that

should be practical.

In CAWP, most of the above processing steps are

realized together with the mentioned properties. The

details of them will be given in subsection 4.2.

3 COMBINATORIAL AUCTIONS

CAs can be categorized according to certain criteria

described below:

1. Categorization based on bidding style

• Open-Bid Combinatorial Auctions: Bidders are

aware of competing bidders’ bids. All bids are

publicly announced.

• Sealed-Bid Combinatorial Auctions: Each bidder

is only aware of his/her bids. After bidding

process is completed and winner is determined, it

can be announced. Hiding the bids is necessary

during bidding time.

2. Categorization based on the number of goods

• Single-Unit Combinatorial Auctions: Amount of

the each individual item is one. For example, if

there are five identical items, they must be

placed to the auction as different items which

have the same product information.

• Multi-Unit Combinatorial Auctions: Amount of

the individual items may be more than one.

3. Categorization based on pricing

• Reserve Combinatorial Auctions: Seller may put

a base acceptance price on each item during

auctioning. Since in CA bundles of items are bid

together, amount of bid should be more than the

sum of the items’ base prices in the bundle.

• Non-Reserve Combinatorial Auctions: Seller

cannot put a base acceptance price to their items

in the auction. Winner(s) pay the amount they

bid and get the items even they are below their

original value.

• Reverse Combinatorial Auctions: Buyers may

want series of items and sellers bid group of that

items. Least expensive bids are accepted.

CAWP implements a Sealed-Bid Single-Unit

Combinatorial Auction mechanism where items can

have reserved prices. They are set by the Auctioneer.

Every item put in an auction is single unit, if two

identical items is needed to be put in an auction, they

should be placed separately.

In CAs, bidders are allowed to express

themselves freely and place any combination of bid

items for the auction. However, this comes with an

explosion of the size of the solution space. Winner

Determination Problem is the problem of deciding

the allocation of winner bids, in a set of bids placed

to the auction, so that the revenue of the auctioneer

can be maximized.

Formally, let I be the set of items under

consideration and R

be the set of non-negative real

numbers. Then, we say that a bid b = (I

, P

,) is an

element of S = (2

- {Ø}) × R

. That means any

subset of power set of items I other than the empty

set may have an assigned value decided by its

bidder. Let B be a subset of S. A set F

⊆

B is said to

be feasible if

∀

b,c

∈

F, c

≠

b and I

∩ I

= Ø. That is

no two items in bidding subsets are the same. Also,

let Φ(B) be the set of all possible feasible allocations

for B. Further, let I(B)=

Bb∈

∪ I

be the set of goods

contained in the bids of B.

Definition 1

: Winner Determination Problem is to

find an allocation W

∈

Φ(B) such that

∀

∈

Φ(B) the

following should hold

∑

∈∈

≤

Such allocation is said to be optimal or revenue

maximizing (Brown et.al., 1999).

WDP is hard because one would need to check

all subset of the bids to identify whether they are

feasible (no conflict of items) and how much

revenue they may provide. A feasible subset of the

bids that has the maximum revenue is the optimal

solution. There are 2

subsets of bids where k being

the number of bids (Cramton et.al, 2006).

In general, there are three main factors affecting

the solution time for a given WDP instance. These

are the number of goods, number of bids and

distribution of the bids. If there are some dominant

bids in the system, solution can be found in

dramatically shorter time. This is because when a

solver accepts a dominant bid, it helps maximizing

the auctioneer revenue and reduces the solution

space, causing a solution to be found faster.

Combinatorial Auction Structured Search

(CASS) (Brown et.al., 1999) and Combinatorial

Auction Branch on Bids (CABOB) (Sandholm et.al.,

2001) are two known algorithms for efficient

solution of WDP:

1. Combinatorial Auction Structured Search

(CASS) Algorithm: CASS uses exhaustive search for

determining optimal solution. It suggests a simple

brute-force search approach supported by four

ICE-B 2010 - International Conference on e-Business

significant heuristic improvements. CASS structures

(or shapes) the search space in order to avoid

conflicting bids with some overlaping items. It keeps

the result of the searches done up to a point and

prunes the search tree. Together with CASS, a test

suite is developed to create sample auction setups

and to test the systems performance. This test suite

is known as CATS (Cramton et.al., 2007)(Brown

et.al., 2000).

2. Combinatorial Auction Branch on Bids

(CABOB) algorithm: CABOB is a tree search

algorithm where tree is branched on bids. It makes a

dept-first Branch&Bound search on the tree.

Branch&Bound search provides a systematic

enumeration of all possible solutions and it prunes

large subsets of fruitless candidate solutions by

using upper and lower bounding (Land and Doig,

1960). In CAWP, we prefered to use a solver that

supports the CASS algorithm.

4 COMBINATORIAL AUCTION

WEB PLATFORM

In this section CAWP will be introduced, with its

functionalities according to the system and the user

requirements. Technical details and performance

results and a comparison with another CA system

are also given.

4.1 General Properties of CAWP

Among the six steps describing complete trading

process (given in subsection 2.2), CAWP fully

supports the steps 1, 2, 4 and 5. Related to step 3,

there is no advertisement support but the users can

see and join directly to (or just observe) the product

sets open to bidding. Also, there is neither payment

nor good delivery tracking capabilities of the

system. The requirements for a typical online

auction system has also been given in subsection

2.2. Most of these requirements are satisfied by

CAWP as described below:

Loser bids are not made known to all bidders

(anonymity). Bidder logs in to the system before

bidding so a winner is always identified (non-

cancelability). Public verification of the winning bid

is really the highest value is not possible. This is

because the loser bids are not announced publicly.

Note that even this could be the case; such

verification would require re-solving the WDP under

consideration. The only mechanism against

impersonation is the username/password usage.

Impersonation of another bidder is not possible

without stealing their user name and password

(unforgeability). A person can impersonate another

person in the CAWP, and jeopardize the fairness of

the trade, but after single act this person can be

notified and receive bad comments, or it can go to

account suspension. CAWP prevents bidders to

place invalid bids, and keeps the auction process

uninterrupted (robustness). In CAWP bids or bidders

have no priority (fairness). Finally, because of the

algorithmic complexity of the WDP problem, for

some problem instances the computation of

determining and verifying a winner bid may not be

practical (efficiency of bidding). In CAWP, this

problem is tried to be handled by putting “at most 30

item per auction” rule for sellers. By this way, one

can get a response from the WDP solver in an

acceptable time.

Below is the list of implemented CAWP

properties based on system/user requirements that

are considered during development:

• Authentication of the users is a must for both

bidding and creating auctions.

• Any internet user can enter to the CAWP site and

view the products information and auctions.

However, user must be logged in to get bidding

and auctioning capabilities.

• There is no hierarchy or priority between users of

the system.

• The system provides its auctioneers to set some

parameters of the auction including auction

name, auction end time, items in the auction,

items’ base prices.

• Bidders can bid any bundle of items as long as

they are in the same auction.

• The system assists bidders with the minimum

acceptable amount of bid being the sum of base

prices of items in the bid.

• Users can withdraw their bids until bidding

session is over.

• Auctioneer can drop an auction if there are no

bids placed on any goods in the auction.

• Buyers and sellers can write comments about the

people they trade with.

• Platform has an internal messaging system.

Sellers and buyers can send private messages to

each other.

• Number of items that can be on a single auction

is maximum 30.

• Real procurement of the goods is realized

between seller and buyer. CAWP only gives

buyers and sellers capability to comment about

their actual trading experiences.

CAWP - A Combinatorial Auction Web Platform

4.2 Technical Details and Performance

Results

Technically, CAWP is constituted from four main

components. The first one is the web-component

using which users can create auctions, and make bid.

The winner determination problem is generated and

results are notified via this component. Second

component is the solver-component that gets the

problems generated by the web-component, solves

them and returns the solution. Third component is

the database-component which is used by the web

and solver components. Bid, auction, and bidder

information are all kept by database-component.

Solver-component gets necessary data from the

database-component to create the winner

determination problem file. After the solver’s

execution, results are put back into the database. The

last component is the customization- component.

This component is necessary to enable CAWP

without knowing web programming. Site

customization can be achieved by using this

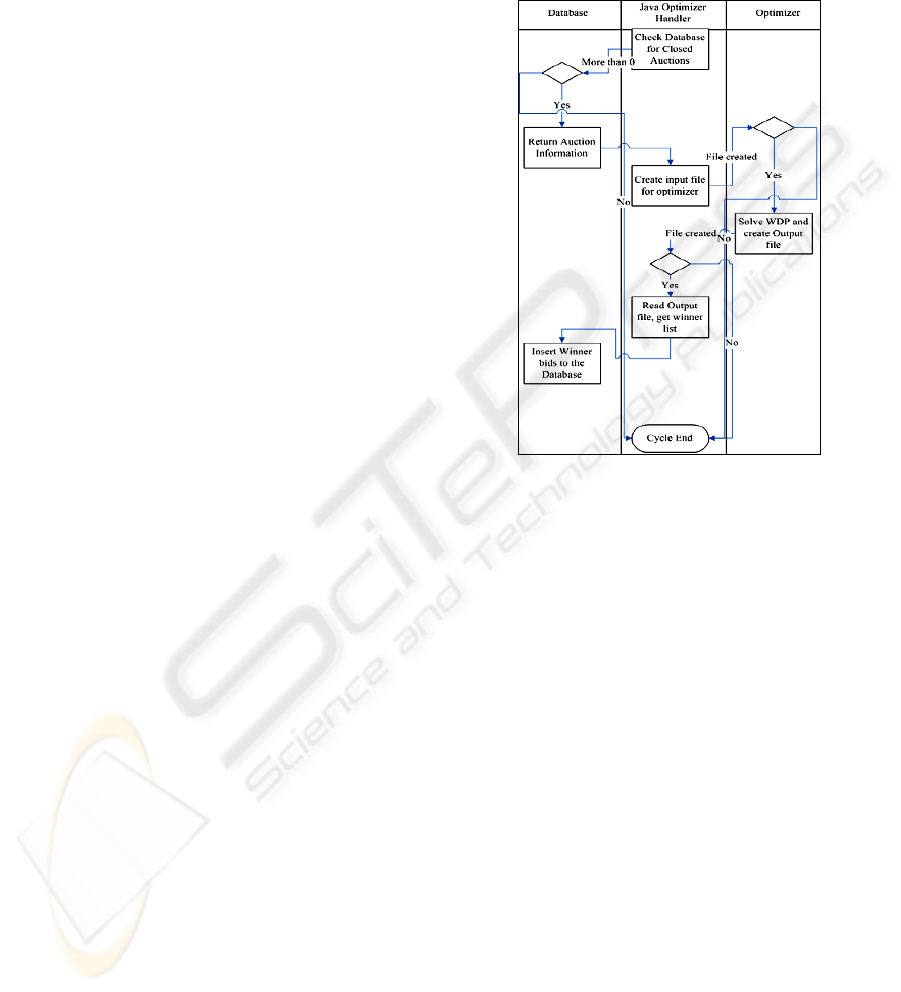
component. Figure 1 shows how WDP solver

program interacts with the remaining components of

the platform. Optimizer-handler seen in Figure 4

aims to provide interoperation of CAWP web

platform and the CASS solver. Throughout the

process, the handler plays the main control-unit role.

It first checks whether there exists a WDP to be

solved or not. If any, it translates the problem

description kept in the database to the acceptable

format of the CASS solver. Concurrently, it calls the

CASS solver. Consequently, the problem is solved,

the result is taken as generated output file, and put

back into the database.

All technologies used in CAWP are open source.

The overall system performance clearly depends on

the performance of the technologies used.

Performance issues related to the database system

and web server that are used can be found in

(MySQL, 2005) and (Apache, 2009), respectively.

Aside from these, the critical component that effects

the general performance is clearly the WDP solver.

The relative performance of the CASS solver has

been evaluated in (Brown and Shoham, 2009). In

order to be able to better tuning of the CAWP

system, we executed a series of performance test

scenarios on Intel® Core™2 Duo 2.66 GHz CPU,

4GB Ram, Windows XP Professional environment.

We created 10 different scenarios for every different

number of good and bid instances. The test scenarios

are generated with CATS tool (Brown et.al.,

2000).Table 1 shows the average completion time of

the executions in seconds. Even if there are 5000

bids to a single auction, the solver can still produce

an answer within minutes. Also, if the number of

bids is small even the auctions with greater number

goods can be solved quickly. But still the major

parameter that effects the solution time is the

number of goods.

Figure 1: WDP solver interaction schema.

When we keep the number of bids as 5000 and

increase the number of goods from 30 to 50 the

completion time of the problem increases from

151.860 seconds to 3713.246 seconds, dramatically.

Increasing number of concurrent CASS solvers

running on a single machine reduces the overall

performance of the system (see Table 2). If aim is to

increase the throughput of the system, concurrent

solvers should run on different machines. One solver

per processor gives the highest expected

performance. The results in Table 2 are obtained by

taking runs on a dual core machine where two or

more solvers run on different CPUs.

In Figure 2, the NPC aspect of the problem solving

operation can be seen. The completion time is

sensitive to the number of goods variable I

especially when I reaches to 50.Note that the CAWP

system is not evaluated by their users in terms of its

usability, yet.

ICE-B 2010 - International Conference on e-Business

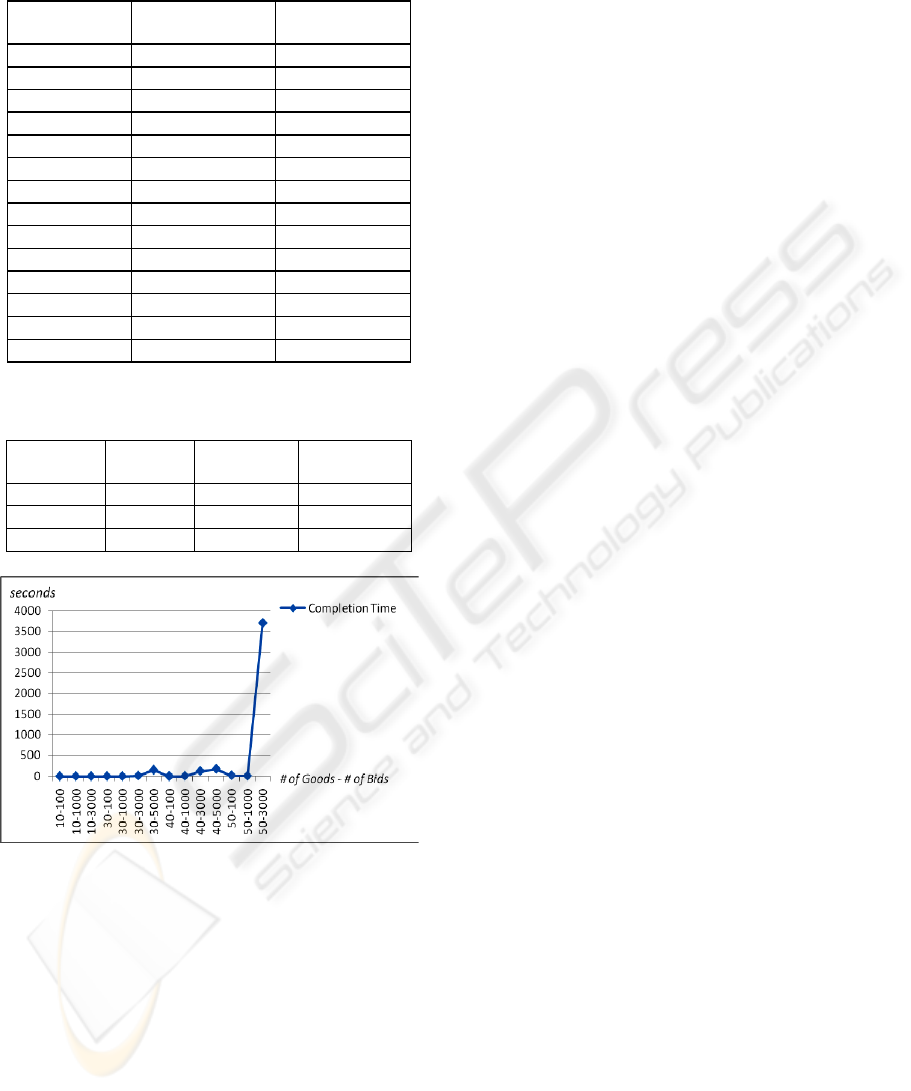
Table 1: Average completion time results for the system

tests.

Number of

Goods

Number of Bids

Results

(in seconds)

10 100 0.002

10 1000 0.016

10 3000 0.210

30 100 0.003

30 1000 0.047

30 3000 12.840

30 5000 151.860

40 100 0.015

40 1000 6.552

40 3000 126.017

40 5000 177.721

50 100 0.020

50 1000 8.424

50 3000 3713.246

Table 2: Performance results for many solvers running on

a two- processor machine.

# of

Solvers

# of

Goods

# of

Bids

Results

(in seconds)

2 30 3000 17.34

3 30 3000 23.87

4 30 3000 35.31

Figure 2: Completion time results for different instances of

number of goods and number of bids pairs.

Finally, for our comparative purpose, we considered

an example CA system namely Online Iterative

Combinatorial Auction System (OICAS) (Fang and

Wang, 2005). It is a prototype system implemented

using Visual Basic and Microsoft Access. OICAS

has following characteristics:

• The auctioneer can determine who can

participate in an auction.

• Only legitimate users (bidders) can participate in

an auction.

• Bidders can bid for any bundle of items with

acceptable price.

• The system tells bidders the required minimum

winning price for their bids automatically.

The main difference between OICAS and CAWP is

that OICAS is an offline prototype implemented in

Microsoft Visual Basic language and Microsoft

Access database. On the other hand, CAWP is a true

web application implemented using PHP for server

side scripting, MySql for database management,

Java for implementing optimizer handler, and C for

the WDP solver. These components can be deployed

and run on different machines. Also, although

OICAS permits its auctioneers to choose their

bidders, CAWP believes in the fairness for the

bidders and it does not allow an auction to be limited

for only a certain group of bidders.

4.3 An Example CAWP Usage For

Custom Built Furniture

Combinatorial Auctioning

A carpenter producing custom built furnitures can

sell combinations of his products via CAWP in order

to increase his revenue. However he needs a

technical assistance to deploy and public his

furniture combinatorial auction website, if otherwise

he can do it himself. As the first step each different

product categories are introduced to the system.

Then an auctioneer account for the carpenter should

be created. A list of available products to be

auctioned are entered to the system by giving

product name, category, description, picture, serial

number and reserve price. Following this, an auction

instance including auction name, duration and list of

target items is generated. The auctioneer can open

more than one auction. After this the bidding period

is started. Within the auction period the system

accepts bids from its registered users. For each bid

the bidders should give the list of items to bid on and

a valid price. By the end of auction period the

system automatically initiates the optimizer in order

to solve the generated WDP problem. The bidding

results are announced at the site in individual basis.

In other words a bidder is only informed about his

winning status, rather then the others. For the time

being the rest of the trading process is not supported

by the system. On the other hand the auctioneer or

the bidders can enter comments about their

experience with the trading process.

CAWP - A Combinatorial Auction Web Platform

5 CONCLUSIONS

In this paper, an online combinatorial auctioning

platform CAWP is introduced. The platform

provides its users to create and to participate in

combinatorial auctions without having to care about

either the complexity of the WDP or its efficient

solution. The performance requirement of the system

is clearly more higher than a typical online

auctioning system. This is mainly due to the required

involvement with an NP-Complete WDP problem.

In our solution different technologies combined

together and integrated under the platform. The

technologies include server side web scripting,

database management, solver handler, and the WDP

solver. All these technologies, except the WDP

solver have been created, originally. Using open

source technologies enabled us to build an operating

system independent platform.

In future, CAWP is planned to be supported by a

third party payment system in order to achieve better

trading opportunities. Also, the system may support

a realistic mechanism to reward and penalize its

users. A better WDP solver or a general purpose

solver package can be adapted to the system in order

to still increase the WDP solution performance.

REFERENCES

Vries S., Vohra R. 2010. Combinatorial Auctions: A

Survey. http://www.cis.upenn.edu/~mkearns/teaching/

cgt/combinatorial-auctions-survey.pdf. As of April

2010

Kwon R.H., Lee C., Ma Z., 2005. An Integrated

Combinatorial Auction Mechanism for Truckload

Transportation Procurement. In: Technical Report,

Mechanical and Industrial Engineering, the University

of Toronto.

Milgrom P., 2000. Putting Auction Theory to Work: The

Simultaneous Ascending Auction. In: Journal of

Political Economy, Vol. 108, No. 2.

Koboldt C., Maldoom D., Marsden R., 2003. The First

Combinatorial Spectrum Auction. In: DotEcon DP

http://www.dotecon.com/publications/dp0301.pdf. As

of April 2010

Lin S., Chen B., Liu C., Soo W., 2008. Web Service

Allocations Based on Combinatorial Auctions and

Market-based Mechanisms. In: Computer Supported

Cooperative Work in Design (CSCWD 2008), vol., iss.

Page(s):452 - 458

Walsh W.E., Wellman M., Ygge F., 2000. Combinatorial

Auctions for Supply Chain Formation. In: ACM

Conference on Electronic Commerce.

Cramton P., Shoham Y., Steinberg R., 2007. An Overview

of Combinatorial Auctions. In: ACM SIGecom

Exchanges, Vol. 7, No. 1.

Gottlob G., Greco G., 2007. On The Complexity of

Combinatorial Auctions: Structured Item Graphs and

Hypertree Decompositions. In: Electronic Commerce

archive: Proceedings of the 8th ACM conference on

Electronic commerce

San Diego, California, USA

Pages: 152 - 161

Cereci İ., 2009. CAWP: A Combinatorial Auction Web

Platform. MSc Thesis, Atılım University, Ankara,

Turkey.

Bakos Y., 1998. The Emerging Role of Electronic

Marketplaces on the web. In: Communications of the

ACM 41(9), pg 35–42.

Wolfram|Alpha, 2009. eBay as a financial entity. In Site:

”http://www02.wolframalpha.com/input/?i=eBay&a=*

C.eBay-_*Financial-“. As of August 2009.

Klemperer P., 2004. A Survey of Auction Theory. In

Book:

Auctions: Theory and Practice. Publisher:

Princeton University Press.

Kumar M., Feldman S., 1998. Internet Auctions. In:

Proceedings of the 3rd conference on USENIX

Workshop on Electronic Commerce - Volume 3 pp.5.

Omote K, 2002. A Study on Electronic Auctions. In: Japan

Advanced Institute of Science and Technology in

partial fulfillment of the requirements for the degree of

Doctor of Philosophy

Brown K.L., Fujishima Y., Shoham Y., 1999. Taming the

Computational Complexity of Combinatorial

Auctions: Optimal and Approximate Approaches. In:

Proceedings of the Sixteenth International Joint

Conference on Artificial Intelligence.

Cramton P., Shoham Y., and Steinberg R., 2006.

Combinatorial Auctions, The MIT press.

Sandholm T., Suri S., Gilpin A., Levine D., 2001. CABOB

A Fast Optimal Algorithm for Combinatorial

Auctions. In:

Seventeenth International Joint

Conference on Artificial Intelligence (IJCAI).

Brown K. L., Pearson M., Shoham Y., 2000. Towards a

Universal Test Suite for Combinatorial Auction

Algorithms. In:

ACM Conference on Electronic

Commerce.

Land A. H., Doig A. G., 1960. An automatic method of

solving discrete programming problems. In:

Econometrica 28

MySQL, 2005. MySQL Performance Benchmarks:

Measuring MySQL’s Scalability and Throughput. In:

A MySQL® Technical White Paper, March 2005.

Apache, 2009. Apache Performance Notes: In Site:

http://httpd.apache.org/docs/1.3/misc/perf-tuning.html

As of August 2009.

Brown K. L., Shoham Y., 2009 Empirical Hardness

Models: Methodology and a Case Study on

Combinatorial Auctions. In: Journal of the ACM, Vol.

56, No. 4, Article 22.

Fang L., Wang Y., 2005. OICAS: An Online Iterative

Combinatorial Auction System. In: IEEE

International Conference on Systems, Man and

Cybernetics.

ICE-B 2010 - International Conference on e-Business