Towards a Multi-camera Mouse-replacement Interface

John Magee, Zheng Wu, Harshith Chennamaneni, Samuel Epstein

Diane H. Theriault and Margrit Betke

Computer Science Department, Boston University

111 Cummington St, Boston, MA 02215 U.S.A.

Abstract. We present our efforts towards a multi-camera mouse-replacement

system for computer users with severe motion impairments. We have worked

with individuals with cerebral palsy or multiple sclerosis who use a publicly-

available interface that tracks the user’s head movements with a single video cam-

era and translates them into mouse pointer coordinates on the screen. To address

the problem that the interface can lose track of the user’s facial feature due to

occlusion or spastic movements, we started to develop a multi-camera interface.

Our multi-camera capture system can record synchronized images from multiple

cameras and automatically analyze the camera arrangement. We recorded 15 sub-

jects while they were conducting a hands-free interaction experiment. We recon-

structed via stereoscopy the three-dimensional movement trajectories of various

facial features. Our analysis shows that single-camera interfaces based on two-

dimensional feature tracking neglect to take into account the substantial feature

movement in the third dimension.

1 Introduction

Camera-based human-computer interaction via analysis of head movement has been

studied for many years (e.g. [1–3]). Early work has typically focused on single-camera

interfaces for entertainment, control of electronic devices (e.g., the remote control of

a TV), and support of automated speech analysis. Camera-based human-computer in-

teraction systems that serve as assistive communication tools have had an enormous

impact on the lives of individuals with severe motion impairments [4,5]. These systems

function as mouse-replacement software that allow users to control a computer mouse

pointer with head movements. The movements of the user’s head [6], nose [4,5,7] or

other features [4] are converted into movements of the mouse pointer on the screen. To

mimic the functionality of a left mouse click, a mouse replacement system typically

evaluates the length of time that the pointer dwells over an icon, button, or menu item

(or its surrounding region) and then issues a selection command.

Currently available video-based mouse-replacement systems for people with severe

disabilities process the input video captured by a single camera. We propose a multi-

camera approach to alleviate the problems with track failures that such systems en-

counter in practice. Track failures occur when facial features become occluded during

tracking, for example, when extreme head rotations result in self-occlusion of the fea-

ture. Track failures also occur due to involuntary rapid movements of users with spastic

cerebral palsy. In addition, multiple camera systems may be able to use information

Magee J., Wu Z., Chennamaneni H., Epstein S., H. Theriault D. and Betke M.

Towards a Multi-camera Mouse-replacement Interface.

DOI: 10.5220/0003001700330042

In Proceedings of the 10th International Workshop on Pattern Recognition in Information Systems (ICEIS 2010), page

ISBN: 978-989-8425-14-0

about the user’s motion in three dimensions to provide better control of the mouse

pointer.

Data from more than one camera allows for use of a conﬁdence measure computed

from detecting and tracking the objects in different images and evaluating if they are

consistent [8]. This may alleviate the problem of feature loss due to occlusion. For

example, when the feature movesout of the ﬁeld of vision of one of the cameras (the left

nostril is occluded because the user turns left), the tracking of the feature is continued

in another camera’s ﬁeld of view. We propose a camera placement that ensures that the

ﬁelds of views of the cameras partially overlap. With this setup, if the feature is lost in

one camera view, the tracker can use another camera view to continue tracking.

To facilitate research on multi-camera assistive technology, we developed a system

that allows processing of images that are captured simultaneously from multiple cam-

eras. Our Multi-Camera Capture (MCC) system provides the general framework for

working with n cameras and has been tested using up to four cameras simultaneously.

The scope of the current project is limited to the following contributions:

1. We provide a software system that enables images to be recorded from multiple

cameras.

2. We createda newdatabase of videos of 15 subjects that are simultaneously recorded

from three camera views while they were performing an interaction task.

3. We present a preliminary stereoscopic analysis of the three-dimensional trajectories

of facial features during interaction experiments.

Our system uses inexpensivewebcams, arranged on a desk in a typical human-computer

interaction environment (Fig. 1), in contrast to expensive calibrated multi-camera cap-

ture systems in controlled laboratory environments. There is a need in the computer

vision community to create data sets with which 3D face tracking systems can be eval-

uated [9]. This applies both to systems that use multiple cameras [9–12] or a single

camera [13]. We hope that other computer-vision research groups will make use of our

capture system and data, and help move forward the research on reliable communication

systems for people with disabilities.

Fig.1. A setup of the Multi Camera Capture system with three cameras. The cameras are the

three silver-colored spheres on top of the laptop display.

2 Methods

Our system divided into three modules, a multi-camera capturing module that provides

temporal calibration, a module that evaluates the geometric relationship between the

cameras and provides spatial calibration, and a third module that provides stereoscopic

reconstruction of three-dimensional (3D) coordinates.

The ﬁrst module, the Multi Camera Capture (MCC) program, records images from

the cameras simultaneously and stores them. The second module performs camera cal-

ibration, that is to recover each camera’s focal length, principal point, radial distortion

coefﬁcients (the “intrinsic parameters,” which make up the camera matrix K) and spa-

tial relationship between objects and cameras (the “extrinsic parameters” of rotation

R and translation t). To estimate the intrinsic parameters, we use a planar calibration

object chessboard with known physical size (Fig. 2). The use of a planar object allows

us to focus on just two coordinates of each three-dimensional object point and deter-

mine the homography H, which maps points (X, Y, 1)

on the object plane to points

(x, y, 1)

on the image plane, i.e., (x, y, 1)

= H · (X, Y, 1)

. We are interested in

estimating H because it encodes the camera matrix K, the rotation matrix R, and the

translation vector t:

H = s K[r

t], (1)

where s is a scale factor and r

and r

are ﬁrst two columns of the rotation matrix R.

With a sufﬁcient number of pairs of points on the chessboard and their correspond-

ing image points, the matrix H can be estimated using Singular Value Decomposition

(SVD). With several images of the chessboard, oriented differently towards the camera,

we can estimate multiple homography matrices H

for the same camera matrix K. The

fact that vectors r

and r

are orthonormal provides additional constraints. Matrix K is

then estimated by solving a system of linear equations [14].

The intrinsic parameters of each camera, given by matrix K, only need to be esti-

mated once and can then be used for stereoscopic reconstruction by our multi-camera

capture system. To estimate the extrinsic parameters, we reuse the chessboard images

to estimate the “fundamental matrix” that relates the coordinates of a feature in the

image of one camera to the coordinates of the feature in the corresponding image of an-

other camera. The program automatically estimates the positions of the corresponding

points of pattern corners in each camera view. In particular, given the two-dimensional

coordinates q

= (x

, y

)

of a point in the ith camera view and the two-dimensional

coordinates q

= (x

, y

)

of a corresponding point in the jth camera view, the funda-

mental matrix relates the two via the equation

= 0. (2)

The entries of the matrix F

can be estimated using the 8-point algorithm [15], whose

name comes from the number of corresponding point pairs (q

, q

) that are used as

input. Matrix F

can also be estimated by using signiﬁcantly more point pairs, incor-

porating the 8-point algorithm into a RANSAC framework [16]. It labels point pairs

that do not agree with the most probable result as outliers. These point pairs may have

been incorrectly identiﬁed as corresponding points. RANSAC is a non-deterministic al-

gorithm that iterates through the possibilities of matrix entries until a desired level of

accuracy is achieved. The desired level of accuracy is speciﬁed as a probability that the

computed matrix is the most likely among all possible matrices. The set of point pairs

used as input to the RANSAC algorithm may yield a number of all possible subsets of

8 corresponding points that is so large (e.g., order of millions) that it is computationally

expensive to compute all matrices exhaustively.

Fig.2. A screenshot of the Multi Camera Capture system while it is used to record images simul-

taneously from two cameras in an experiment. In the ﬁeld of view of the two cameras is a board

with a checker pattern, which is used for spatial calibration of the cameras.

Our spatial calibration module calls the RANSAC method on 40 point pairs and

uses an OpenCV function [14] to estimate the entries of the fundamental matrix. Our

method uses a 99%-probability level as the desired accuracy threshold. If this threshold

yields a number of outlier pairs that exceeds 12 (i.e., 12/40 ≈ 30% of the pairs), the

points collected for stereo calibration are deemed to be insufﬁciently accurate, and a

new calibration process is run.

Once the fundamental matrix F

is determined, we can estimate the “essential ma-

trix” E

that encodes the absolute position and orientation of the two cameras:

= K

. (3)

To obtain the coordinates of corresponding points in three-dimensional world coordi-

nates, we need to estimate the projection matrix P = K[R |t] of each camera. We

assign the origin of the world-coordinate system to the center of projection of our ﬁrst

camera, which means that P

= K

[I |0]. The projection matrices P

of the other

cameras can then be constructed through SVD factorization of the essential matrices

[15]. The projection matrices are stored by our calibration module and used for 3D

reconstruction through triangulation by the third module of our system.

Our program relies on the known calibration device, the chessboard, for the calibra-

tion procedure. As an alternative, we have tracked distinctive features such as a human

eye through several frames of each camera and used feature correspondences to per-

form self-calibration [15], that is, to estimate both intrinsic and extrinsic parameters for

all cameras at the same time. The unknown scale can be estimated by measuring the

physical distance between tracked features, e.g., the distance between a person’s eyes.

3 Experiments and Results

We used a three-camera version of our multi-camera interaction system to record 15

subjects while they were conducting a human-computer interaction experiment. The

Fig.3. Left: A screenshot of the Camera Mouse interface used in the experiments. Right: A

screenshot of the ClickTester program. The user was instructed to move the mouse pointer into the

target circle, highlighted in red, with head movements that were detected by the Camera Mouse.

The ClickTester program presented a sequence of target circles to the user that was designed so

that signiﬁcant mouse pointer movements and changes in movement directions were required.

group of subjects included 8 men and 7 women. Most subjects had dark hair. Two sub-

jects wore glasses. For each subject, we recorded three image sequences using three

Logitech Orbit MP cameras (Fig. 1). The cameras were not radiometrically calibrated

and each used automatic gain control. The recordings were synchronized by our tem-

poral calibration module so that temporally corresponding images were identiﬁable.

Prior to the hands-free human-computer interaction experiment, the fundamental

matrices for all pairs of cameras were estimated and stored using our spatial calibration

module. We numbered the cameras from left to right starting with 0. Our system then

provided an estimate of the fundamentalmatrices F

, F

and F

that relate the image

coordinatesof cameras 0 and 1, 1 and 2, and 0 and 2, respectively.The spatial calibration

module was executed before every subject test was performed in order to ensure spatial

calibration via the three fundamental matrices. The camera positions were not disturbed

during the recording.

We used the publicly-available assistive technology “Camera Mouse” [4,17] (Fig. 3

left), which is a single-camera mouse-replacement system for people with severe mo-

tion impairments. We initialized the Camera Mouse using the standard mouse by se-

lecting a facial feature (eyebrow corner) to track. The region around the corner of an

eyebrow contains signiﬁcant brightness changes, which makes it a reliable feature to

track.

Our system recorded three image streams while the test subjects were moving their

heads signiﬁcantly (Fig. 4). We developed test software, called “Click Tester,” that pro-

vided a movement protocol and ensured that all subjects were recorded with various

head positions and orientations.

The ClickTester software displays eight circles on the screen, one of which is high-

lighted (see Fig. 3, right). In our experiments, the subject was asked to move the mouse

pointer onto the highlighted circle using the Camera Mouse. When the subject had

Fig.4. Images collected at different points in time during the human-computer interaction exper-

iment. Each row shows the three simultaneously-recorded frames as captured by the left, center,

and right cameras. The subject’s head orientation differs signiﬁcantly from row to row and the

subject’s left eye is occluded in the right camera view in the second row. Similarly, the subject’s

right eye is occluded in the left camera view in the third row. The lack of radiometrical calibration

of the cameras and the use of separate automated gain controls resulted in images with different

intensity levels. This is particularly noticeable in the images recorded by the right camera, which

are darker than the images recorded by the left and center cameras.

moved the mouse pointer to the highlighted circle, a new circle was highlighted. The

subject was asked to repeat the process until all circles were visited. The software was

designed as a means to simulate a realistic use of a camera-based mouse-replacement

system that involved signiﬁcant head motions. It also records the trajectory of the mouse

pointer for further analysis.

Among the head motions that the subjects performed was a gesture in which the

subjects moved their heads ﬁrst upwards and then diagonally to the lower left. One of

the subjects performing this gesture is shown in Fig. 5. His gesture lasted about three

seconds, which corresponded to 17 frames. Ten of these 17 frames, as recorded by each

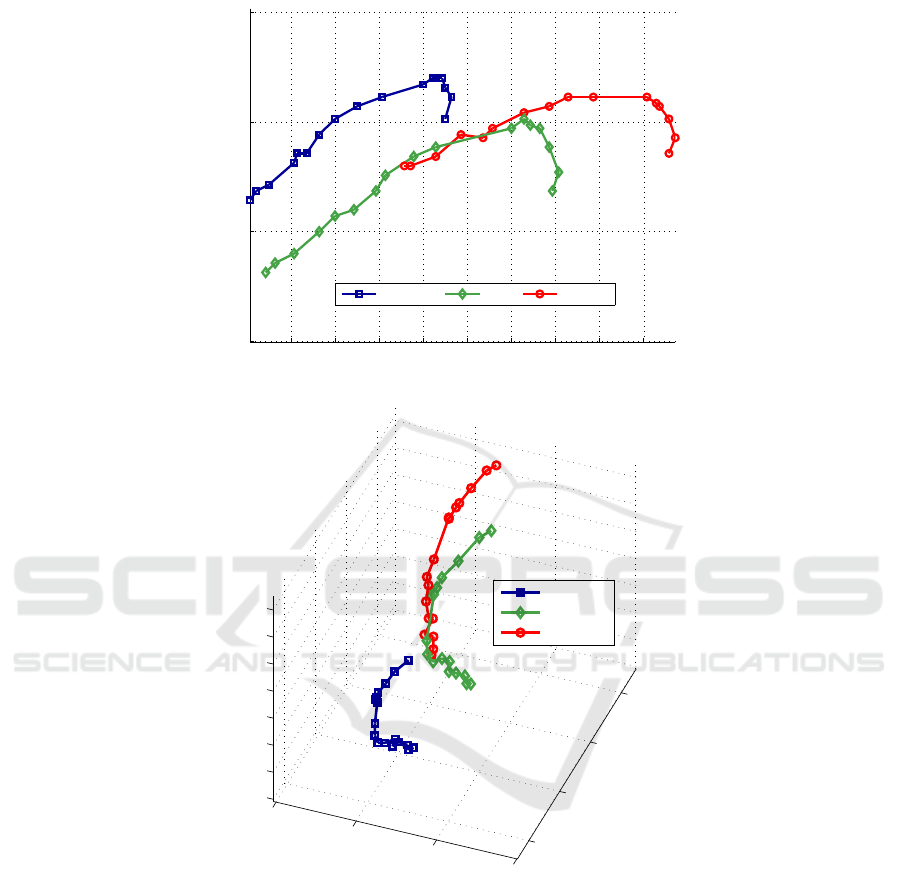
of the three cameras, are shown in Fig. 5. We reconstructed the 3D positions of the

outer corners of the subject’s eyes and his nose tip during the head gesture. The 3D

trajectories of the three features are shown in Fig. 6. We placed the 3D scene coordinate

system so that its x and y axes were aligned with the image plane of the left camera and

the z axis was normal to and pointed away from the image plane. The origin of the 3D

scene coordinate system was placed at the location of the nose tip in the ﬁrst frame of

the left camera view.

During the gesture, the features moved on average 18.5 cm in the 3D scene. It

is noteworthy that, during the head gesture, the features moved 4.6 cm in the direc-

tion away from the left camera when the user directed the mouse pointer to the top

of the computer screen. The features then moved back 3.0 cm towards the left camera

when the user moved the mouse pointer to a region near the left corner of the screen.

This component of a user’s head movement cannot be taken into account by a single-

camera mouse-replacement interface that is based on two-dimensional tracking of the

feature projected into the image plane. The conversion from image-feature coordinates

to mouse-pointer screen coordinates is typically implemented as a linear transforma-

tion in single-camera mouse-replacement systems. This means that the user is required

to exert more efforts to move the mouse pointer in the outer regions of the computer

screen than to move it within the center region of the screen. This may be particularly

signiﬁcant for individuals who have very limited head movements. It motivates imple-

mentations of nonlinear transfer functions [6], for example, based on distance to the

center of the screen.

4 Discussion and Conclusions

We presented our research efforts towards developing a multi-camera mouse-replace-

ment system for computer users with severe motion impairments. We have several

years of experience working with individuals who use the “Camera Mouse,” a publicly-

available interface system that tracks the computer user’s head movements with a single

video camera and translates them into the movements of the mouse pointer on the com-

puter screen. To address the problem that the Camera Mouse can lose track of facial

features due to occlusion or spastic movements, we started to develop a multi-camera

interface that provides (1) redundant input so that there is not a single point of tracking

failure and (2) additional stereoscopic information to improve system reliability.

Our current multi-camera capture system can record synchronized images from

multiple cameras showing different but, as typically desired, overlapping views of the

same scene. Our system also automatically analyzes the geometry of the camera ar-

rangement. It uses inexpensive webcams that can be placed on a desk in a typical

human-computer interaction arrangement.

We used a three-camera version of our system to record 15 subjects while they were

conducting a hands-free human-computer interaction experiment in real time. For this

experiment, we developed a testing program that guided the subjects in making various

head movements that resulted in signiﬁcant mouse pointer movements and changes in

movement directions. For each subject, we recorded three image sequences that were

synchronized so that corresponding images were identiﬁable.

Our system provided the information about the geometry of any pair of cameras rel-

ative to one another. We reconstructed via stereoscopy the three-dimensional movement

trajectories of various features such as the eyes and nose tip. Our analysis shows that

single-camera interfaces based on two-dimensional feature tracking neglect to take into

account the substantial feature movement in the third dimension.

1 3 5 7 8

10 12 14 16 17

Fig.5. Cropped images of a user during our human-computer interaction experiment with the

ClickTester program. Each column shows simultaneously recorded images from the left, center,

and right cameras with the corresponding frame number (time stamp) on top. During the exper-

iment, the user ﬁrst selected a target circle at the top of the screen, which resulted in a raising

of his head. He then moved the mouse pointer to a target circle near the lower left corner of the

screen, which resulted in a turning and lowering of his head.

30 32 34 36 38 40 42 44 46

X−Axis (cm)

Y−Axis (cm)

Right Eye Nose Left Eye

−12

−10

−8

−6

−4

−2

X−Axis (cm)

Y−Axis (cm)

Z−Axis Depth (cm)

Right Eye

Nose

Left Eye

Fig.6. Reconstructed 3D feature trajectories. Numbers indicate time stamps. Top: 3D points in

the x-y plane that is parallel to the left camera. Bottom: This viewing angle shows the signiﬁcant

feature movement in the z direction, ﬁrst away and then towards the camera.

Acknowledgements

We would like to thank the human subjects who spared time from their busy schedules

to participate in the experiments. Funding for this work was provided by the National

Science Foundation, HCC grant IIS-0713229.

References

1. A. H. Gee and R. Cipolla. Tracking faces. In R. Cipolla and A. Pentland, editors, Computer

Vision for Human-Machine Interaction, pages 113–122. Cambridge University Press, 1998.

2. W. T. Freeman, D. Anderson, P. Beardsley, C. Dodge, H. Kage, K. Kyuma, Y. Miyake,

M. Roth, K. Tanaka, C. Weissman, and W. Yerazunis. Computer vision for interactive com-

puter graphics. IEEE Computer Graphics and Applications, 18(3):42–53, May 1998.

3. M. Turk and R. George. Perceptual user interfaces. Comm. of the ACM, 43(3), 2000.

4. M. Betke, J. Gips, and P. Fleming. The camera mouse: Visual tracking of body features to

provide computer access for people with severe disabilities. IEEE Transactions on Neural

Systems and Rehabilitation Engineering, 10(1):1–10, 2002.

5. J. Varona, C. Manresa-Yee, and F. J. Perales. Hands-free vision-based interface for computer

accessibility. Journal of Network and Computer Applications, 31(4):357–374, 2008.

6. R. Kjeldsen. Improvements in vision-based pointer control. In 8th International ACM

SIGACCESS Conference on Computers and accessibility (Assets ’06), pages 189–196, 2006.

7. D. O. Gorodnichy and G. Roth. Nouse ’use your nose as a mouse’ perceptual vision tech-

nology for hands-free games and interfaces. Image and Vision Computing, 22(12):931–942,

2004.

8. E. A. Cansizoglu and M. Betke. An information fusion approach for multiview feature

tracking. In 20th International Conference on Pattern Recognition (ICPR 2010), Istanbul,

Turkey, 2010. 4 pp.

9. T. K. Marks, J. R. Hershey, and J. R. Movellan. Tracking motion, deformation, and texture

using conditionally Gaussian processes. IEEE Transactions on PatternAnalysis and Machine

Intelligence, 32(2):348–363, 2010.

10. C. John, U. Schwanecke, and H. Regenbrecht. Real-time volumetric reconstruction and

tracking of hands and face as a user interface for virtual environments. In VR 2009: IEEE

Virtual Reality Conference, pages 241–242, 2009.

11. M. R¨atsch, C. Blumer, G. Teschke, and T. Vetter. Coarse-to-ﬁne particle ﬁlters for multi-

object human computer interaction. In IEEE International Workshop on Intelligent Data Ac-

quisition and Advanced Computing Systems: Technology and Applications (IDAACS 2009),

pages 440–445, September 2009.

12. K. Sidorov, Y. Hicks, D. Marshall, S. Sanei, and J. Chambers. Real time multi camera 3D

tracking system. In 3rd European Conference on Visual Media Production (CVMP 2006),

page 191, London, UK, 2006.

13. F. Dornaika and B. Raducanu. Three-dimensional face pose detection and tracking using

monocular videos: Tool and application. IEEE Transactions on Systems, Man, and Cyber-

netics, Part B: Cybernetics, 39(4):935–944, 2009.

14. G. Bradski and A. Kaehler. Learning OpenCV, chapter 11-12. O’Reilly, 2008.

15. R. I. Hartley and A. Zisserman. Multiple View Geometry in Computer Vision. Cambridge

University Press, 2003.

16. M. A. Fischler and R. C. Bolles. Random sample consensus: a paradigm for model ﬁtting

with applications to image analysis and automated cartography. Communications of the

ACM, 24(6):381–395, 1981.

17. Camera Mouse – Innovative software for people with disabilities,

http://www.cameramouse.org, accessed April 2010.