GENETIC HEURISTICS FOR REDUCING MEMORY ENERGY

CONSUMPTION IN EMBEDDED SYSTEMS

Maha Idrissi Aouad

INRIA Nancy, Grand Est / LORIA, 615 Rue du Jardin Botanique, 54600 Villers-L

es-Nancy, France

Ren

e Schott

IECN, LORIA, Nancy-Universit

e, Universit

e Henri Poincar

e, 54506 Vandoeuvre-L

es-Nancy, France

Olivier Zendra

INRIA Nancy, Grand Est / LORIA, 615 Rue du Jardin Botanique, 54600 Villers-L

es-Nancy, France

Keywords:

Energy consumption reduction, Genetic heuristics, Memory allocation management, Optimizations.

Abstract:

Nowadays, reducing memory energy has become one of the top priorities of many embedded systems design-

ers. Given the power, cost, performance and real-time advantages of Scratch-Pad Memories (SPMs), it is not

surprising that SPM is becoming a common form of SRAM in embedded processors today. In this paper, we

focus on heuristic methods for SPMs careful management in order to reduce memory energy consumption.

We propose Genetic Heuristics for memory management which are, to the best of our knowledge, new origi-

nal alternatives to the best known existing heuristic (BEH). Our Genetic Heuristics outperform BEH. In fact,

experimentations performed on our benchmarks show that our Genetic Heuristics consume from 76.23% up

to 98.92% less energy than BEH in different conﬁgurations. In addition they are easy to implement and do not

require list sorting (contrary to BEH).

1 INTRODUCTION

Reducing energy consumption of embedded systems

is a topical and very crucial subject. Many sys-

tems are energy-constrained and, despite batteries

progress, these systems still have a limited auton-

omy. Numerous systems are concerned: small one

and large one. Small systems are mainly our daily

life objects, such as: cell phones, laptops, PDAs, MP3

players, etc. For the large systems, we have clusters,

mainframes, super computers, etc. These systems are

more and more energy greedy. Accordingly, memory

will become the major energy consumer in an embed-

ded system. In fact, trends in (ITRS, 2007) show that

Systems on Chip (SoC) consumption is dominated

by dynamic and static memory consumption and that

memory will occupy a larger place in SoC.

Thus, different options to save energy, hence in-

crease autonomy, exist. These various approaches can

be classiﬁed in two main categories: hardware opti-

mizations and software optimizations. Hardware

techniques fall beyond the scope of this paper, but a

large amount of literature about them is available (see

ﬁrst parts of (Graybill and Melhem, 2002)). In this

paper, we will focus on software, compiler-assisted

techniques in order to optimize energy consumption

in memory.

Most authors rely on Scratch-Pad Memories

(SPMs) rather than caches. The interested reader can

look at (Benini and Micheli, 2000) for a comprehen-

sive list of references. Cache memories, although they

help a lot with program speed, do not always ﬁt in

embedded systems. In fact, cache memory is ran-

dom access memory (RAM) that a computer micro-

processor can access more quickly than it can access

regular RAM. As the microprocessor processes data,

it looks ﬁrst in the cache memory and if it ﬁnds the

data there (from a previous reading of data), it does

not have to do the more time-consuming reading of

data from larger memory (Tanenbaum, 2005). But

caches increase the system size and its energy cost be-

cause of cache area plus managing logic. In contrast,

394

Idrissi Aouad M., Schott R. and Zendra O. (2010).

GENETIC HEURISTICS FOR REDUCING MEMORY ENERGY CONSUMPTION IN EMBEDDED SYSTEMS.

In Proceedings of the 5th International Conference on Software and Data Technologies, pages 394-402

DOI: 10.5220/0003002503940402

 SciTePress

SPMs have interesting features. SPM also known as

local store in computer terminology, is a high-speed

internal memory used for temporary storage of calcu-

lations, data, and other work in progress. It can be

considered as similar to an L1 cache in that it is the

memory next closest to the ALU’s after the internal

registers, with explicit instructions to move data from

and to main memory. Like cache, therefore, SPM

consists of small, fast SRAM, but the main difference

is that SPM is directly and explicitly managed at the

software level, either by the developer or by the com-

piler, whereas cache requires extra dedicated circuits.

Its software management makes it more predictable

as we avoid cache miss cases which is an important

feature in real-time embedded systems. Compared

to cache, SPM thus has several advantages (Idrissi

Aouad and Zendra, 2007). SPM requires up to 40%

less energy and 34% less area than cache (Banakar

et al., 2002). Further, the run-time with an SPM us-

ing a simple static knapsack-based (Banakar et al.,

2002) allocation algorithm is 18% better as compared

to a cache. Contrarily to (Banakar et al., 2002), (Ben

Fradj et al., 2005) distinguish between static and dy-

namic energy. They also show the effectiveness of us-

ing an SPM in a memory architecture where a saving

about 35% in energy consumption is achieved when

compared to a memory architecture without an SPM.

(Absar and Catthoor, 2006) use statistical methods

and the Independent Reference Model (IRM) to prove

that SPMs, with an optimal mapping based on ac-

cess probabilities, will always outperform the direct-

mapped cache, irrespective of the layout inﬂuencing

the cache behavior. Additionally, SPM cost is lower.

The rest of the paper is organized as follows. Sec-

tion 2 describes some existing heuristics and related

works for managing memory data allocation. Section

3 presents our approach based on Genetic Heuristics

to ﬁnd the optimized memory data allocation in order

to reduce energy consumption. Section 4 gives the

memory energy consumption model we used in or-

der to estimate the energy consumed by our different

heuristics. Section 5 shows the various experimen-

tal results obtained. Finally, Section 6 concludes and

gives some perspectives.

2 EXISTING HEURISTICS AND

RELATED WORKS

The approaches presented in this section try to help in

determining the optimized memory allocation in or-

der to reduce energy consumption according to mem-

ory type (access speed, energy cost, large number of

miss access cases, etc.) and application behavior. In

order to do so, these methods use proﬁle data to gather

memory access frequency information. This informa-

tion can be collected either statistically by analyzing

the source code of the application or dynamically by

proﬁling the application (number of times that data is

accessed, data size, access frequency, etc.).

In these techniques, because of the reduced size

of SRAM, one tries to optimally allocate data in it

in order to realize energy savings. An approach is to

place interesting data in memory with a low access

cost (SPM) whereas the other data will be placed in a

memory with low storage cost (DRAM). Thus, most

of the authors use one of the three following strate-

gies:

Allocate Data into SPM by Size. The smaller data

are allocated into SPM as there is space available else

they are allocated in DRAM. This method has the ad-

vantage of being simple to implement since it only

considers the size of the data but has the disadvan-

tage of allocating the largest data in the main memory

(DRAM). These largest data could be often accessed,

which will imply a very few energy economy.

Allocate Data into SPM by Number of Accesses.

The most frequently accessed/used data are allocated

into SPM as there is space available else they are al-

located in DRAM. This strategy is optimal than the

previous one, since the most frequently accessed/used

data will be allocated in a memory that consumes less

energy and therefore will achieve more savings as ex-

plained and demonstrated in (Sj

odin et al., 1998) and

(Steinke et al., 2002). However, we can note granular-

ity problems in some cases such as a structure which

only one part is often accessed/used.

Allocate Data Memory into SPM by Number of

Accesses and Size (BEH). This is somehow a com-

bination of the two previous strategies. The idea here

is to combine their advantages. If we consider the ex-

ample of a structure in which only a part is the most

frequently accessed/used, we take into account the av-

erage number of access to this structure. This avoids

granularity problems. Here, data are sorted according

to their ratio (access number/size) in descending or-

der. The data with the highest ratio is allocated ﬁrst

into SPM as there is space available. Otherwise it

is allocated in DRAM. This heuristic uses a sorting

method which can be computationally expensive for

a large amount of data. In addition to that, this sorting

method will not work very well in a dynamic perspec-

tive where the maximum capacity of the SPM is not

known in advance. This is, so far, the best known ex-

isting heuristic (BEH).

GENETIC HEURISTICS FOR REDUCING MEMORY ENERGY CONSUMPTION IN EMBEDDED SYSTEMS

395

In these techniques, most authors model the prob-

lem as a 0/1 integer linear programming (ILP) prob-

lem and then use an available IP solver to solve it.

The main trade-offs between these approaches re-

volve around the objects considered (arrays, loops,

global, heap or stack variables, etc.). In (Avissar et al.,

2002), because of the reduced SRAM size, the least

used variables are ﬁrst allocated to slower memory

banks (DRAM), while the most frequently used vari-

ables are kept in fast memory (SRAM) as much as pos-

sible. They consider global and stack variables and

choose between SPM and cache, while (Steinke et al.,

2002; Wehmeyer et al., 2004) consider global vari-

ables, functions and basic blocks and choose between

SPM banks. When (Udayakumaran et al., 2002) con-

sider static and global variables and choose between

SPM banks also. The previous techniques are all

based on the frequency of data accesses. In contrast,

another approach is to focus on data that is the most

cache-conﬂict prone (Panda et al., 1997), (Truong

et al., 1998). In the rest of this paper, we will refer

to the strategy BEH as a basis for our memory energy

optimizations.

3 OUR GENETIC APPROACH

Genetic algorithms (GAs) are adaptive methods which

may be used to solve search and optimization prob-

lems. They are based on the genetic processes of bio-

logical organisms (Sivanandam and Deepa, 2007).

By starting with a population of possible solutions

and changing them during several iterations, GAs

hope to converge to the ﬁttest solution. Each solution

is represented through a chromosome, which is just

an abstract representation. The process begins with a

set of potential solutions or chromosomes that are ran-

domly generated or selected. Over many generations,

natural populations evolve according to the principles

of natural selection and survival of the ﬁttest. For gen-

erating new chromosomes, GA can use both crossover

and mutation techniques. Crossover involves splitting

two chromosomes and then, for example, combining

one half of each chromosome with the other pair. Mu-

tation involves ﬂipping a single bit of a chromosome.

The chromosomes are then evaluated using a certain

ﬁtness criterion and the ones which satisfy the most

this criterion are kept while the others are discarded.

This process repeats until the population converges

toward the optimal solution. The basic genetic algo-

rithm is summarized in Figure 1.

There are several advantages to the Genetic Al-

gorithm such as their parallelism and their liability.

They require no knowledge or gradient information

SELECT random population of n chromosomes.

EVALUATE the fitness f(x) of each chromosome

x in the population.

LOOP

SELECT two parent chromosomes from a

population.

CROSS OVER the parents to form new children

with a crossover probability Pc.

MUTATE new children with a mutation

probability Pm.

Place new offspring in the new population.

Use new generated population for a further

sum of the algorithm.

EXIT if the end condition is satisfied and

return best solution.

END LOOP

Figure 1: A basic genetic algorithm.

about the response surface, they are resistant to be-

coming trapped in local optima and they perform

very well for large-scale optimization problems. GAs

have been used as heuristics to solve difﬁcult prob-

lems (such as NP-hard problems) for machine learn-

ing and also for evolving simple programs. Applica-

tions of Genetic Algorithms include: nonlinear pro-

gramming, stochastic programming, signal process-

ing and combinatorial optimization problems such as

the Traveling Salesman Problem, Knapsack Problem,

sequence scheduling, graph coloring (just to name a

few). For further applications, the interested reader

can see (Zheng and Kiyooka, 1999).

3.1 Our Optimization Problem

Our problem is a combinatorial optimization problem

like the famous knapsack problem (H. Kellerer and

Pisinger, 2004). Suppose memory is a big knapsack

and data are items. We want to ﬁll this knapsack that

can hold a total weight of W with some combination

of items from a list of N possible items each with

weight w

and value v

so that the value of the items

packed into the knapsack is maximized. This problem

has a single linear constraint, a linear objective func-

tion which sums the values of the items in the knap-

sack, and the added restriction that each item will be

in the knapsack or not.

If N is the total number of items, then there are 2

subsets of the item collection. So an exhaustive search

for a solution to this problem generally takes expo-

nential running time. Therefore, the obvious brute

force approach is infeasible. Some dynamic program-

ming techniques also have exponential running time,

but have proven useful in practice. Here, we take a

different approach, and investigate the problem using

genetic methods. In this paper, we propose a heuris-

tic based on GAs to solve the problem of optimizing

ICSOFT 2010 - 5th International Conference on Software and Data Technologies

396

the memory data allocation in order to reduce mem-

ory energy consumption. This heuristic outperforms

the best known existing heuristic (BEH) presented in

Section 2 and the Tabu Search heuristic presented in

(Idrissi Aouad et al., 2010).

3.2 Key Elements

In this section, we explain some basic terminologies

and operators we used with our Genetic Heuristics.

• Individual. An individual is a single solution.

• Population. A population is a collection of indi-

viduals. The two important aspects of population

used in GAs are the initial population generation

and the population size. For each problem, the

population size will depend on the complexity of

the problem. Ideally, the initial population should

have a gene pool as large as possible in order to

be able to explore the whole search space. Hence,

to achieve this, the initial population is, in most

of the cases, chosen randomly. In our case, we

randomly selected the initial population.

• Encoding. If N is the total number of data, then

a solution point is just a ﬁnite sequence s of N

terms such that s[n] is either 0 or the size of the

data. s[n] = 0 if and only if the n

data is

not selected in the solution point. This solution

must satisfy the constraint of not exceeding the

maximum SPM capacity (i.e.

∑

i=1

s[i] ≤ C).

• Fitness. The ﬁtness of an individual is the value

of an objective function. The ﬁtness not only in-

dicates how good the solution is, but also corre-

sponds to how close the chromosome is to the op-

timal one. In our Genetic Heuristic, at each stage

(generation), the solution points are evaluated for

ﬁtness (according to how much of the memory ca-

pacity they ﬁll), and the best and worst performers

are identiﬁed.

• Crossover. Crossover is the process of taking

two parent solutions and producing from them a

child. After the selection process, the population

is enriched with better individuals. Here, when

conditions are ripe for breeding, the best solution

mates with a random (non-extreme) solution, and

the offspring replaces the worst one. The child

inherits a part of each parent’s genes. In our Ge-

netic Heuristic, we used the following crossover

techniques and probability:

– Single Point Crossover. The two mating chro-

mosomes are cut once at a randomly selected

crossover point and the sections after the cuts

are exchanged.

– Two Points Crossover. In two points

crossover, two crossover points are chosen ran-

domly and the contents between these points

are exchanged between two mated parents.

– Crossover Probability. Crossover Probabil-

ity (P

) is a parameter to describe how often

crossover will be performed. If there is no

crossover, offspring are exact copies of par-

ents. If P

= 1, then all offspring are made by

crossover. If P

= 0, whole new generation is

made from exact copies of chromosomes from

old population. Crossover is made in hope that

new chromosomes will contain good parts of

old chromosomes and therefore the new chro-

mosome will be better.

• Mutation. Mutation prevents the algorithm to be

trapped in local optima. It is seen as a background

operator to maintain genetic diversity in the pop-

ulation by varying the gene pool. The genes of a

solution are just its sequence terms. In our Ge-

netic Heuristic, a mutation of a solution is a ran-

dom change of up to half of its current genes. A

gene change sets a term to 0 if the term is currently

nonzero, and sets a term to the corresponding data

size if the term is currently zero.

– Mutation Probability. The mutation proba-

bility (P

) decides how often parts of chromo-

some will be mutated. If there is no muta-

tion, offspring are generated immediately after

crossover without any change. If P

= 1, whole

chromosome is changed, if P

= 0, nothing is

changed. Mutation should not occur very often,

because then GA will in fact change to random

search.

• Search Termination. The termination or conver-

gence criterion brings the search to a halt. There

are various stopping conditions: the maximum

number of generations reached, after a speciﬁed

time has elapsed, if there is no change to the

population’s best ﬁtness for a speciﬁed number

of generations or during an interval of time, etc.

Here, we stop the Genetic Heuristic after a certain

amount of time.

4 MEMORY ENERGY

ESTIMATION MODEL

In order to compute the energy cost of the system

for each conﬁguration, we propose in this section an

energy consumption estimation model for our con-

sidered memory architecture composed by an SPM,

GENETIC HEURISTICS FOR REDUCING MEMORY ENERGY CONSUMPTION IN EMBEDDED SYSTEMS

397

a DRAM and an instruction cache memory. In our

model, we distinguish between the two cache write

policies: write-through and write-back. In a Write-

Through cache (WT), every write to the cache causes

a synchronous write to the DRAM. Alternatively, in a

Write-Back cache (WB), writes are not immediately

mirrored to the main memory. Instead, the cache

tracks which of its locations have been written over

and then, it marks these locations as dirty. The data in

these locations is written back to the DRAM when

those data are evicted from the cache (Tanenbaum,

2005). Our proposed energy consumption estimation

model is presented below:

E = E

tspm

+ E

tic

+ E

tdram

E = N

spmr

∗ E

spmr

(1)

+ N

spmw

∗ E

spmw

(2)

icr

∑

k=1

∗ E

icr

+ (1 − h

) ∗ [E

dramr

+ E

icw

+(1 −WP

) ∗ DB

∗ (E

icr

+ E

dramw

)]] (3)

icw

∑

k=1

[W P

∗ E

dramw

+ h

∗ E

icw

+ (1 −W P

) ∗

(1 − h

) ∗ [E

icw

+ DB

∗ (E

icr

+ E

dramw

)]](4)

+ N

dramr

∗ E

dramr

(5)

+ N

dramw

∗ E

dramw

(6)

Lines (1) and (2) represent respectively the total

energy consumed during a reading and during a writ-

ing from/into SPM. Lines (3) and (4) represent re-

spectively the total energy consumed during a read-

ing and during a writing from/into instruction cache.

When, lines (5) and (6) represent respectively the total

energy consumed during a reading and during a writ-

ing from/into DRAM. The various terms used in our

energy consumption estimation model are explained

in Table 1.

5 EXPERIMENTAL RESULTS

For our experiments, we consider a memory archi-

tecture composed by a Scratch-Pad Memory, a main

memory (DRAM) and an instruction cache mem-

ory. We make sure to take similar features for the

cache memory and the SPM in order to compare

their energy performance fairly. We performed ex-

periments with eleven benchmarks from six differ-

ent suites: MiBench (Guthaus et al., 2001), SNU-

RT, M

alardalen, Mediabenchs, Spec 2000 and Wcet

Benchs. Table 2 gives a description of these bench-

marks.

Table 1: List of terms.

Term Meaning

tspm

Total energy consumed in SPM.

tic

Total energy consumed in instruction

cache.

tdram

Total energy consumed in DRAM.

spmr

Energy consumed during a reading

from SPM.

spmw

Energy consumed during a writing

into SPM.

spmr

Reading access number to SPM.

spmw

Writing access number to SPM.

icr

Energy consumed during a reading

from instruction cache.

icw

Energy consumed during a writing

into instruction cache.

icr

Reading access number to instruction

cache.

icw

Writing access number to instruction

cache.

dramr

Energy consumed during a reading

from DRAM.

dramw

Energy consumed during a writing

into DRAM.

dramr

Reading access number to DRAM.

dramw

Writing access number to DRAM.

W P

The considered cache write policy:

WT or WB. In case of WT, W P

= 1

else in case of WB then W P

= 0.

Dirty Bit used in case of WB to

indicate during the access k if the

instruction cache line has been

modiﬁed before (DB

= 1) or

not (DB

= 0).

Type of the access k to the instruction

cache. In case of cache hit, h

= 1.

In case of cache miss, h

= 0.

In order to compute the energy cost of the sys-

tem for each conﬁguration, we used our developed en-

ergy consumption estimation model presented in Sec-

tion 4. This model is based on the OTAWA frame-

work (Cass

e and Rochange, 2007) to collect informa-

tion about number of accesses and on the energy con-

sumption estimation tool CACTI (Wilton and Jouppi,

1996) in order to collect information about energy

per access to each kind of memory. OTAWA (Open

Tool for Adaptative WCET Analysis) is a frame-

work of C++ classes dedicated to static analyses of

programs in machine code and to the computation

of Worst Case Execution Time (WCET). OTAWA is

freely available (under the LGPL license) and is de-

signed to support different architectures like Pow-

erPC, ARM or M68HC. In our case, we focus on

ICSOFT 2010 - 5th International Conference on Software and Data Technologies

398

Table 2: List of benchmarks.

Benchmark Suite Description

Sha MiBench The secure hash

algorithm that

produces a 160-

bit message digest

for a given input.

Bitcount MiBench Tests the bit

manipulation

abilities of a

processor by

counting the

number of bits

in an array

of integers.

Fir SNU-RT Finite impulse

response ﬁlter

(signal processing

algorithms) over

a 700 items

long sample.

Jfdctint SNU-RT Discrete-cosine

transformation on

8x8 pixel block.

Adpcm M

alardalen Adaptive pulse

code modulation

algorithm.

Cnt M

alardalen Counts non-

negative numbers

in a matrix.

Compress M

alardalen Data compression

using lzw.

Djpeg Mediabenchs JPEG decoding.

Gzip Spec 2000 Compression.

Nsichneu Wcet Benchs Simulate an

extended Petri net.

Automatically

generated code

with more than

250 if-statements.

Statemate Wcet Benchs Automatically

generated code.

PowerPC architectures. In our model, we distinguish

between the two cache write policies: Write-Through

(WT) and Write-Back (WB) as explained in Section

4. Our presented Tabu Search algorithm and the BEH

strategy have been implemented with the C language

on a PC Intel Core 2 Duo, with a 2.66 GHz proces-

sor and 3 Gbytes of memory running under Mandriva

Linux 2008.

5.1 Genetic Heuristics with Both

Crossover and Mutation

In this subsection, we investigate the performances of

our Genetic Heuristics using both genetic operators:

crossover and mutation. These genetic operators are

explained in Section 3.2. After making experiments

on the standard benchmarks presented in Table 2, we

ﬁnd that our Genetic Heuristics achieve the same en-

ergy savings as BEH. This is what we were expecting,

due to the fact that they both give the optimal solution

thanks to our developed backtracking algorithm. This

is true for the standard benchmarks we use as they

contain uniform data leading to a big number of lo-

cal minima. Thus, in order to put some trouble in the

BEH strategy and see if it still gives the best solution,

we decided to modify slightly our benchmarks. Con-

cretely, our modiﬁcation consists in adding one vari-

able to each benchmark. This variable is very com-

mon to all benchmarks as it performs an output (so

did not change the benchmarks features) and is big

enough to provide energy savings if it is chosen for an

SPM allocation. We refer to a modiﬁed benchmark as

benchmarkCE.

In these experiments, we generate 30 different ex-

ecutions for each of our Genetic Heuristics as the so-

lution given differs from an execution to another. Ge-

netic 1 represents the results obtained for P

= 0.1,

= 0.5 and for a single point crossover. Genetic 2

represents the results obtained for P

= 0.1, P

= 0.5

and for a two points crossover. When Genetic (1,2)

refers to the average results obtained on 30 executions

of Genetic 1 and 30 executions of Genetic 2. We mix

them that way, as the results obtained with Genetic 1

are equal to those obtained with Genetic 2.

Figure 2 presents the results obtained when com-

paring BEH and our Genetic Heuristics on our mod-

iﬁed benchmarks assuming the write-back cache pol-

icy. In the following, as the shapes of curves obtained

when comparing BEH and Genetic Heuristics on the

modiﬁed benchmarks assuming the Write-Through

cache policy (WT) or the Write-Back cache policy

(WB) are slightly the same, only the results obtained

with the write-back cache policy are plotted. One can

show that E

W T mode

6= E

W Bmode

As we can see from this ﬁgure, Genetic (1,2)

achieves better performances than BEH on energy

savings on our benchmarks. In fact, these results

show that Genetic (1,2) consumes from 78.18%

(StatemateCE) up to 98.92% (ShaCE) less energy

than BEH in the WT mode on one hand. On the

other hand, Genetic (1,2) consumes from 76.23%

(StatemateCE) up to 98.92% (ShaCE) less energy

than BEH in the WB mode.

GENETIC HEURISTICS FOR REDUCING MEMORY ENERGY CONSUMPTION IN EMBEDDED SYSTEMS

399

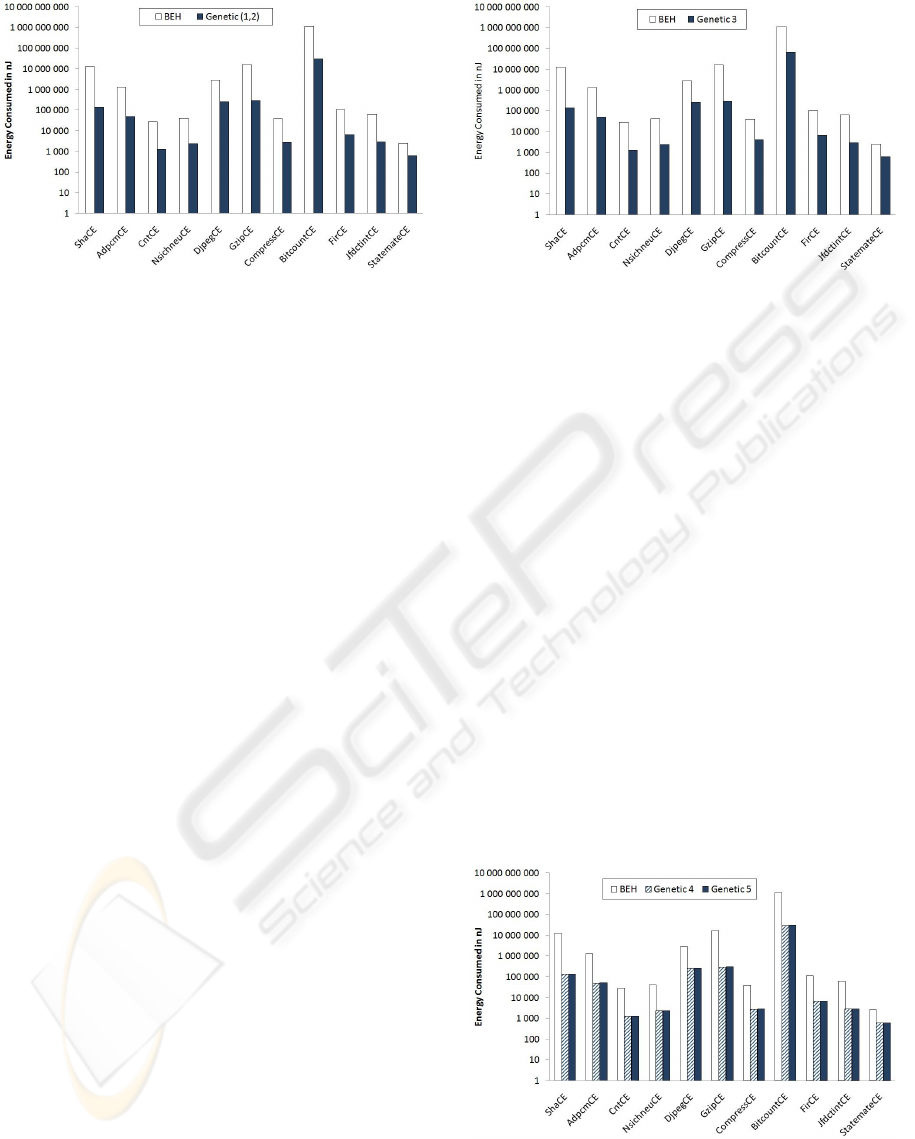
Figure 2: Energy consumed by modiﬁed benchmarks with

WB mode.

For BEH, although we used the modiﬁed bench-

marks, we still obtain the same energy savings as with

the standard benchmarks. The BEH strategy did not

give the optimal solution anymore as one could expect

as proven by our developed backtracking algorithm,

but Genetic (1,2) gives it. This is normal due to the

fact that BEH is a sort of access number/size of data as

we explain in Section 2. The variable we add in each

benchmark has a given access number/size (this ratio

depends on the data proﬁling of each benchmark) so

that this variable is not a priority in the sorting made

by the BEH method. This is done on purpose so that

when it will be the turn of this variable to be treated

by BEH, the remaining space in the SPM will not be

enough to take this variable and hence it will be allo-

cated in main memory. Whereas, an optimal solution

would be to start by allocating this variable ﬁrst into

the SPM. In contrast, our Genetic Heuristics are ro-

bust enough to overcome this problem and ﬁnd the

optimal solution as it can be noticed.

5.2 Genetic Heuristics with either

Crossover or Mutation

In this subsection, we look if removing mutation or

crossover operator has a real impact on the perfor-

mances of our Genetic Heuristics. Curious to know

more, we decided to make some additional experi-

ments. First, we start by omitting the crossover op-

eration. In these experiments, we generate 30 differ-

ent executions for our Genetic Heuristic as the solu-

tion given differs from an execution to another. These

results are average results obtained on 30 executions

of Genetic 3. Where: Genetic 3 represents the re-

sults obtained for P

= 0.5. Figure 3 presents the re-

sults obtained when comparing our Genetic Heuris-

tic to BEH on our modiﬁed benchmarks assuming the

write-back cache policy and without crossover. Re-

minding that E

W T mode

6= E

W Bmode

Figure 3: Energy consumed by modiﬁed benchmarks with

WB mode without crossover.

As we can see from this ﬁgure, Genetic 3 achieves

better performances than BEH on energy savings on

our benchmarks. In fact, these results show that Ge-

netic 3 consumes from 78.18% (StatemateCE) up to

98.92% (ShaCE) less energy than BEH in the WT

mode on one hand without crossover. On the other

hand, Genetic 3 consumes from 76.23% (Statem-

ateCE) up to 98.92% (ShaCE) less energy than BEH

in the WB mode without crossover.

Then, we continue by omitting the mutation oper-

ation. In these experiments, we generate 30 different

executions for each of our Genetic Heuristics as the

solution given differs from an execution to another.

Genetic 4 represents the results obtained for a single

point crossover. Genetic 5 represents the results ob-

tained for a two points crossover. These results are

average results obtained on 30 executions of Genetic

4 and 30 executions of Genetic 5. Figure 4 shows the

results obtained when comparing our Genetic Heuris-

tics to BEH on our modiﬁed benchmarks assuming

the write-back cache policy and without mutation.

Reminding that E

W T mode

6= E

W Bmode

Figure 4: Energy consumed by modiﬁed benchmarks with

WB mode without mutation.

As we can see from Figure 4, both Genetic 4 and

Genetic 5 achieve better performances than BEH on

ICSOFT 2010 - 5th International Conference on Software and Data Technologies

400

energy savings on our benchmarks. In fact, these re-

sults show that both Genetic 4 and Genetic 5 consume

from 78.18% (StatemateCE) up to 98.92% (ShaCE)

less energy than BEH in the WT mode on one hand

without mutation. On the other hand, both Genetic 4

and Genetic 5 consume from 76.23% (StatemateCE)

up to 98.92% (ShaCE) less energy than BEH in the

WB mode without mutation.

In some cases, it is not necessary to apply both

genetic operators (crossover and mutation) to achieve

good results. Thus, omitting one of the two genetic

operators still allows GAs to converge. In fact, we can

see that our Genetic Heuristics outperforms BEH on

the modiﬁed benchmarks. Regardless if we are using

either crossover or mutation operator or both of them,

we achieve the same energy savings on our modiﬁed

benchmarks.

6 CONCLUDING REMARKS

AND FURTHER RESEARCH

ASPECTS

In this paper, we have proposed a general energy con-

sumption estimation model able to be adapted to dif-

ferent memory architecture conﬁgurations. We also

have proposed new Genetic Heuristics for reducing

memory energy consumption in embedded systems

which are more efﬁcient than the best known existing

method (BEH). In fact, our Genetic Heuristics man-

age to consume nearly from 76% up to 98% less mem-

ory energy than BEH in different memory conﬁgura-

tions. In addition our Genetic Heuristics are easy to

implement and do not require list sorting (contrary to

BEH). Comparisons of execution times of BEH and

Genetic Heuristics will be included in the full ver-

sion of this paper. In future work, we plan to ex-

plore hybrid heuristics and other evolutionary heuris-

tics (Markov Decision Processes, Simulated Anneal-

ing, ANT method, Particle Swarm technique, etc.) for

solving the problem of reducing memory energy con-

sumption.

ACKNOWLEDGEMENTS

The authors are grateful to anonymous referees for

their comments and suggestions.

This work is ﬁnanced by the french national re-

search agency (ANR) in the Future Architectures pro-

gram.

REFERENCES

Absar, J. and Catthoor, F. (2006). Analysis of scratch-pad

and data-cache performance using statistical methods.

In ASP-DAC, pages 820–825.

Avissar, O., Barua, R., and Stewart, D. (2002). An opti-

mal memory allocation scheme for scratch-pad-based

embedded systems. Transaction. on Embedded Com-

puting Systems., 1(1):6–26.

Banakar, R., Steinke, S., Lee, B., Balakrishnan, M., and

Marwedel, P. (2002). Scratchpad memory: design al-

ternative for cache on-chip memory in embedded sys-

tems. In CODES, pages 73–78, New York, NY, USA.

ACM Press.

Ben Fradj, H., Ouardighi, A. E., Belleudy, C., and Auguin,

M. (2005). Energy aware memory architecture con-

ﬁguration. In MEDEA ’04: Proceedings of the 2004

workshop on MEmory performance, volume 33, pages

3–9. ACM.

Benini, L. and Micheli, G. D. (2000). System-level power

optimization: techniques and tools. IEEE Design and

Test, 17(2):74–85.

Cass

e, H. and Rochange, C. (2007). OTAWA, Open

Tool for Adaptative WCET Analysis. In De-

sign, Automation and Test in Europe (Poster ses-

sion ”University Booth”) (DATE), Nice, 17/04/07-

19/04/07, page (electronic medium), http://www.date-

conference.com/. DATE. Poster session.

Graybill, R. and Melhem, R. (2002). Power aware com-

puting. Kluwer Academic Publishers, Norwell, MA,

USA.

Guthaus, M. R., Ringenberg, J. S., Ernst, D., Austin, T. M.,

Mudge, T., and Brown, R. B. (2001). Mibench: A

free, commercially representative embedded bench-

mark suite. In WWC ’01: Proceedings of the Workload

Characterization, 2001. WWC-4. 2001 IEEE Interna-

tional Workshop, pages 3–14, Washington, DC, USA.

IEEE Computer Society.

H. Kellerer, U. P. and Pisinger, D. (2004). Knapsack Prob-

lems. Springer, Berlin, Germany.

Idrissi Aouad, M., Schott, R., and Zendra, O. (2010). A

Tabu Search Heuristic for Scratch-Pad Memory Man-

agement. In ICSET’2010: Proceedings of Interna-

tional Conference on Software Engineering and Tech-

nology. To appear, in press.

Idrissi Aouad, M. and Zendra, O. (2007). A Survey

of Scratch-Pad Memory Management Techniques for

low-power and -energy. In 2nd ECOOP Work-

shop on Implementation, Compilation, Optimization

of Object-Oriented Languages, Programs and Sys-

tems (ICOOOLPS’2007).

ITRS (2007). System drivers. http://www.itrs.net/Links/

2007ITRS/2007 Chapters/2007 SystemDrivers.pdf.

Panda, P. R., Dutt, N., and Nicolau, A. (1997). Efﬁcient

utilization of scratch-pad memory in embedded pro-

cessor applications. In DATE.

Sivanandam, S. N. and Deepa, S. N. (2007). Introduction

to Genetic Algorithms. Springer Publishing Company,

Incorporated.

GENETIC HEURISTICS FOR REDUCING MEMORY ENERGY CONSUMPTION IN EMBEDDED SYSTEMS

401

odin, J., Fr

oderberg, B., and Lindgren, T. (1998). Allo-

cation of global data objects in on-chip ram. In Work-

shop on Compiler and Architectural Support for Em-

bedded Computer Systems. ACM.

Steinke, S., Wehmeyer, L., Lee, B., and Marwedel, P.

(2002). Assigning program and data objects to

scratchpad for energy reduction. In DATE, page 409.

IEEE Computer Society.

Tanenbaum, A. (2005). Architecture de l’ordinateur 5e

edition. Pearson Education.

Truong, D. N., Bodin, F., and Seznec, A. (1998). Improving

cache behavior of dynamically allocated data struc-

tures. In International Conference on Parallel Archi-

tectures and Compilation Techniques (IEEE PACT),

pages 322–329.

Udayakumaran, S., Narahari, B., and Simha, R. (2002). Ap-

plication speciﬁc memory partitioning for low power.

In ACM COLP 2002 (Compiler and Operating Sys-

tems for Low Power). ACM Press.

Wehmeyer, L., Helmig, U., and Marwedel, P. (2004).

Compiler-optimized usage of partitioned memories.

In WMPI.

Wilton, S. and Jouppi, N. (1996). Cacti: An enhanced cache

access and cycle time model. IEEE Journal of Solid-

State Circuits.

Zheng, Y. and Kiyooka, S. (1999). Genetic algorithm appli-

cations. http://www.me.uvic.ca/∼zdong/courses/

mech620/GA App.PDF.

ICSOFT 2010 - 5th International Conference on Software and Data Technologies

402