
A GREEN DECISION SUPPORT SYSTEM FOR INTEGRATED
ASSEMBLY AND DISASSEMBLY SEQUENCE PLANNING
USING A PSO APPROACH
Yuan-Jye Tseng, Fang-Yu Yu and Feng-Yi Huang
Department of Industrial Engineering and Management, Yuan Ze University
135 Yuan-Tung Road, Chung-Li, Taoyuan 320, Taiwan
Keywords: Decision Support System, Product Life Cycle Management, Green Product Life Cycle, Assembly Sequence
Planning, Disassembly Sequence Planning, Particle Swarm Optimization.
Abstract: A green decision support system is presented to integrate assembly and disassembly sequence planning and
to evaluate the two costs in one integrated model. In a green product life cycle, it is important to determine
how a product can be disassembled before the product is planned to be assembled. For an assembled
product, an assembly sequence planning model is required for assembling the product at the start, whereas a
disassembly sequence planning model is needed for disassembling the product at the end. In typical
assembly and disassembly sequence planning approaches, the two sequences and costs are independently
planned and evaluated. In this research, a new integrated model is presented to concurrently generate and
evaluate the assembly and disassembly sequences. First, graph-based models are presented for representing
feasible assembly sequences and disassembly sequences. Next, a particle swarm optimization (PSO)
method with a new encoding scheme is developed. In the new PSO encoding scheme, a particle is
represented by a position matrix defining an assembly sequence and a disassembly sequence. The assembly
and disassembly sequences can be simultaneously planned with an objective of minimizing the total of
assembly costs and disassembly costs. The test results show that the presented method is feasible and
efficient for solving the integrated assembly and disassembly sequence planning problem. An example
product is implemented and illustrated in this paper.
1 INTRODUCTION
In a complete product life cycle of an assembled
product, both an assembly sequence and a
disassembly sequence are required. An assembly
sequence is required to locate and fix the
components in an ordered sequence to construct the
product at the start of the product life cycle. An
assembly sequence can be defined as an ordered
sequence of components and assembly operations
required to produce the final product. The purpose of
assembly sequence planning is to arrange the
assembly sequences based on the assembly
constraints and cost objectives.
On the other hand, a disassembly sequence is
required to disconnect the components of the
product at the end of the product life cycle. A
disassembly sequence can be defined as an ordered
sequence of components and disassembly operations
with which the product can be decomposed into
separated modules or components. The purpose of
disassembly sequence planning to arrange the
disassembly sequences based on the disassembly
constraints and cost objectives.
In a green product life cycle, it is essential to
plan how a product can be disassembled, reused, or
recycled, before the product is actually assembled
and produced. In a green product life cycle, although
the disassembly operations occur at the end, it is
important to plan in advance at the start. Therefore, a
green decision support system is required in a green
product life cycle management system to integrate
assembly sequence planning and disassembly
sequence planning.
In the traditional concept of sequential product
life cycle activities, the assembly sequence planning
and the disassembly sequence planning are
considered as two independent tasks. As a result, the
cost factors in the assembly sequence planning
model may sometimes contradict the cost factors in
444
Tseng Y., Yu F. and Huang F. (2010).
A GREEN DECISION SUPPORT SYSTEM FOR INTEGRATED ASSEMBLY AND DISASSEMBLY SEQUENCE PLANNING USING A PSO APPROACH
.
In Proceedings of the 5th International Conference on Software and Data Technologies, pages 444-449
DOI: 10.5220/0003005504440449
Copyright
c
SciTePress

the disassembly sequence planning model, or vice
versa. Therefore, a good assembly sequence for
constructing a product may result in adding more
costs in the corresponding disassembly sequence. In
this situation, if a product is assembled with an
assembly sequence with a low cost, it may cost more
to disassemble the product. Therefore, the assembly
and disassembly sequences must be concurrently
planned with an integrated model.
In this research, a green decision system is
proposed. The assembly and disassembly sequences
can be analyzed and evaluated with an integrated
planning model. A new PSO encoding scheme is
developed by defining the position of a particle
using a position matrix. The position matrix of a
particle defines an assembly sequence and a
disassembly sequence. In this way, the assembly
sequence and disassembly sequence can be
simultaneously planned by optimizing the position
matrix of a particle. The major contributions lie in
the new concept of integrated assembly and
disassembly sequence planning model and the new
PSO encoding and solution scheme to optimize the
two costs.
In this paper, Section 2 presents a literature
review Section 3 presents the graph-based
representation models for representing the assembly
and disassembly sequences. Section 4 presents the
PSO method for finding the solutions. Section 5
discusses the test results with an example. Finally,
section 6 concludes this study.
2 LITERATURE REVIEW
In the related research in assembly planning, it can
be summarized that assembly planning can be
performed in three stages: (1) assembly modelling
and representation, (2) assembly sequence
generation, and (3) assembly evaluation and
optimization. A recent review can be found in
Abdullah et al. (2003). The previous research in
assembly planning can be classified into three
categories. The first category uses rules or
knowledge bases to perform generation of different
assembly sequences. The second category presents
automatic generation of feasible assembly
sequences using graph representation forms
including the research presented in de Mello and
Sanderson (1991), Lin and Chang (1993), and Choi
et al. (1998). The third category focuses on
assembly analysis and evaluation for searching the
better or the optimal assembly sequence. The
research in this class includes Laperriere and
ElMaraghy (1996), Gottipolu and Ghosh (1997),
and Chen et al. (2004).
The recent research by Su (2007) introduced a
geometric constraint analysis method to generate
assembly precedence relations and evaluate feasible
assembly sequences. Dong et al. (2007) presented a
connection-semantics-based assembly tree hierarchy
to analyze geometric and non-geometric
information.
In the related research in disassembly sequence
planning, a review has been presented by Lambert
(2003). The concept of disassembly precedence
matrix has been applied by Huang and Huang
(2002) and Gungor and Gupta (2001) to evaluate
precedence relationships between components and
to generate disassembly sequences. Torre et al.
(2003) presented disassembly sequence planning
based on precedence relations among components,
sub-assemblies, and product. Kongar and Gupta
(2006) presented a disassembly sequence planning
method using GA.
The PSO has been successfully applied to many
continuous and discrete optimizations (Kennedy and
Eberhart, 1997). Banks et al. (2008) reviewed and
summarized the related PSO research in the areas of
hybridization, combinatorial problems, multiple
objectives and constrained optimization areas.
In this research, a green decision support system
for a complete life cycle management by integrating
assembly and disassembly planning is presented. A
PSO method is developed for finding the solutions
with an objective of minimizing the cost functions.
3 REPRESENTATION MODELS
Two graph-based models are presented to represent
the integrated assembly and disassembly sequences.
(1) Assembly precedence diagram (APD),
(2) Disassembly precedence diagram (DPD).
An assembly precedence diagram (APD) is a
directed graph showing the precedence of the
components and the associated assembly operations.
In this research, the concept of APD is applied to
represent the spatial connectivity relationship and
precedence between two components. The concept is
expanded for use in disassembly planning by
defining the disassembly precedence diagram (DPD).
An example product A is shown in Figure 1. The
APD and DPD of the product A are shown in Figure
2.
A GREEN DECISION SUPPORT SYSTEM FOR INTEGRATED ASSEMBLY AND DISASSEMBLY SEQUENCE
PLANNING USING A PSO APPROACH
445

Component Name
0 Screen cover plate
1 Top case
2 LCD panel
3 Side button
4 Keyboard
5 Front button
6 Frame
7 Printed circuit board
8 Battery
9 Bottom case
10 Battery case
Figure 1: Illustration of the example product A.
Two new matrices forms, assembly precedence
matrix (APM) and disassembly precedence matrix
(DPM), are developed for integrated assembly
planning and disassembly planning. The two matrix
models are shown as follows.
APM =
nnnn
ij
n
ni
i
i
njjj
aaa
a
aa
aaa
p
p
p
ppp
21
2221
12111
2
1
21
(1)
where p
i
and p
j
are components, and n is the number
of components, a value of a
ij
= 0 represents that
there is no precedence between two the components
p
i
and p
j
, a value of a
ij
= 1 indicates that component
p
j
must be assembled before component p
i
.
DPM =
nnnn
ij
n
ni
i
i
njjj
ddd
d
dd
ddd
p
p
p
ppp
21
2221
12111
2
1
21
(2)
where p
i
and p
j
are components, and n is the number
of components, a value of d
ij
= 0 represents that
there is no precedence between two components p
i
and p
j
, a value of d
ij
= 1 indicates that component p
j
must be disassembled before component p
i
.
4 SOLUTION USING PARTICLE
SWARM OPTIMIZATION (PSO)
The overall flow of the PSO method is illustrated in
Figure 2. The PSO algorithm is an evolutionary
computation method introduced by Kennedy and
Eberhard (1997). In PSO, each particle moves
around in the multi-dimensional space with a
position and a velocity. The velocity and position
are constantly updated by the particle’s own
experience and the experience of the whole swarm.
Given a problem, a particle can be encoded to
represent a solution. Each solution, called a particle,
flies in the search space towards the optimal
position.
Figure 2: The overall flowchart of the PSO method.
In a general form, a particle is defined by its
position and velocity. The position of a particle i in
the D-dimension search space can be represented as
X
i
=[x
i1
, x
i2
, …, x
id
, …, x
iD
]. The velocity of the
particle i in the D-dimension search space can be
represented as V
i
=[v
i1
, v
i2
, …, v
id
, …, v
iD
]. Each
particle has its own best position P
i
=[p
i1
, p
i2
, …, p
id
,
…, p
iD
] representing the particle’s personal best
ICSOFT 2010 - 5th International Conference on Software and Data Technologies
446

objective (pbest) at time t. The global best particle is
denoted as p
g
and the best position of the entire
swarm (gbest) is denoted as P
g
=[p
g1
, p
g2
, …, p
gd
, …,
p
gD
] at tie t. To search for the optimal solution, each
particle adjusts its velocity according to the velocity
updating equation and position updating equation.
idgdidid
old
idi
new
id
xprcxprcvwv
2211
,
(3)
where d =1, …, D, i =1, …, E (number of particles),
new
id
v
: the new velocity of i in the current iteration t,
old
id
v
: the velocity of i in the previous iteration (t - 1),
c
1
and c
2
: constants called acceleration coefficients,
w
i
: the inertia weight,
r
1
and r
2
: two independent random numbers with a
uniform distribution [0, 1],
p
id
: the best position of each individual particle i,
p
gd
: the best position of the entire swarm.
new
id
old
id
new
id
vxx
,
(4)
where
new
id
x is the new position in the current
iteration t,
old
id
x is in the previous iteration (t - 1).
4.1 Cost Function
A cost function by integrating the assembly costs
and disassembly costs is formulated and used as an
objective function. The cost items are described as
follows.
(1) Assembly and disassembly operation cost (AOC
and DOC).
(2) Assembly and disassembly instability cost (AIC
and DIC).
(3) Assembly and disassembly directional
accessibility cost (ADC and DDC).
(4) Assembly and disassembly tool setup cost (ATC
and DTC).
(5) Assembly and disassembly weight effect cost
(AWC and DWC).
The value of each of the cost functions is
measured on a consistent scale with a unit in dollars.
The total cost function (TC) is the sum of all the
operation cost functions and can be described using
the following equation:
TC = (AOC+AIC+ADC+ATC+AWC) +
(5)
(DOC+DIC+DDC+DTC+DWC)
4.2 Encoding
In the developed encoding scheme, a particle is
represented by a position matrix. A position matrix
presents an integrated assembly and a disassembly
sequence. The position of particle i, i = 1, …, E, is
represented by a position matrix, denoted as X
ijk
, j =
1, 2, and k = 1, …, N, where N is the number of
components.
The first row, where j = 1, represents an
assembly sequence. In the heuristic sequencing rule,
the values in the first row represent the ranked order
values of the N components in an assembly
sequence. The second row, where j = 2, represents a
disassembly sequence. In the heuristic sequencing
rule, the values in the second row represent the
ranked order values of the N components in an
assembly sequence.
X
ijk
=
11 12 13 1
21 22 23 2
n
n
x
xx x
x
xx x
,
(6)
where i = 1, …, E, j =1, 2, and , k =1, …, N.
In the heuristic rule for decoding an assembly
sequence, the values in the first row [X
11
, X
12
, …,
X
1n
] are sorted in an ascending order. The ranked
order values represent the ordered position of the
component in the assembly sequence. For example,
if the ranked order values of row 1 of (C
1
, C
2
, C
3
, C
4
,
C
5
) are [4.5 1.1 3.2 7.6 5.3], then the ordered
positions of (C
1
, C
2
, C
3
, C
4
, C
5
) are (third, first,
second, fifth, fourth). The assembly sequence is
decoded as (C
2
, C
3
, C
1
, C
5
, C
4
). The heuristic rule
for decoding a disassembly sequence can be
interpreted in the same way.
4.3 The PSO Method for
Integrated Assembly and
Disassembly Planning
The flowchart the PSO method is shown in Figure 3.
Step 1. Setup parameters.
(1) Set iteration t = 0.
(2) T
Number
: the iteration (generation) number.
(3) P
Size
: the number of particles.
Step 2. Initialize a population of particles i = 1, …,
E,with random positions and velocities.
(1) A particle i is defined by a multi-dimensional
position matrix of (2)*(N).
(2) The position of particle i is defined by X
ijk
.
(3) The velocity of particle i is defined by V
ijk
.
Step 3. Evaluate the fitness function.
(1) t = t + 1.
A GREEN DECISION SUPPORT SYSTEM FOR INTEGRATED ASSEMBLY AND DISASSEMBLY SEQUENCE
PLANNING USING A PSO APPROACH
447
(2) Fitness = TC.
Step 4. Update the velocity of each particle i.
idgdidid
old
idi
new
id
xprcxprcvwv
2211
,
new
id
v
is the new velocity in the current iteration t,
old
id
v is the velocity in the previous iteration (t-1),
Step 5. Move the position of each particle i.
new
id
old
id
new
id
vxx
,
where
new
id
x is the new position in the iteration t,
old
id
x is the position in the iteration (t - 1).
Step 6. Check the feasibility of the solution and the
number of iteration t.
(1) The precedence is checked by APM and
DPM.
(2) If (t
> T
Number
), then go to Step 7, else go to
Step 2.
Step 7. Decode the best particle position and
interpret the solution.
5 IMPLEMENTATION AND TEST
RESULTS
In the presented green decision support system, the
models were implemented and tested by developing
software on a personal computer. The example
product A is illustrated in Figure 1. There are 11
components, C
0
, C
1
, …, C
10
. The APD and DPD are
shown in Figure 3.
(a) APD (b) DPD
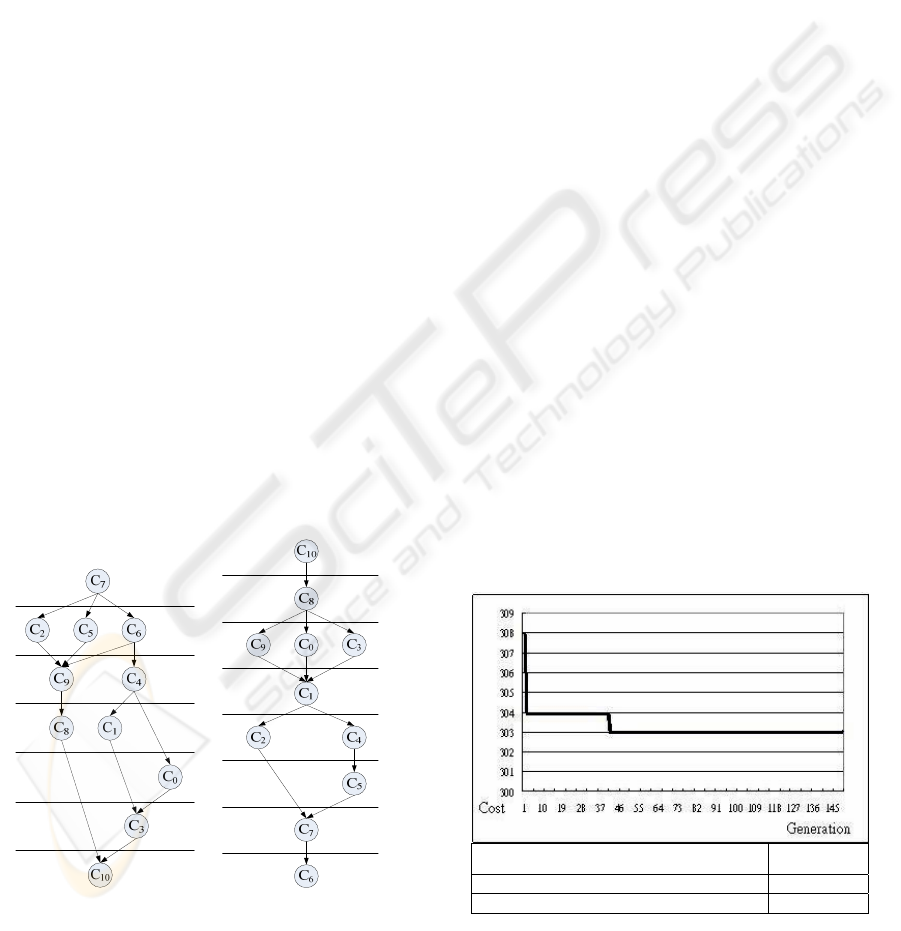
Figure 3: The APD and DPD of the example product A.
The APM and DPM are shown in the following
forms.
0123 45 6789 10
0
1
2
3
4
5
6
7
8
9
10
00001011000
00001011000
00000001000
11001011000
00000011000
00000001000
00000001000
00000000000
00100111010
00100111000
11111111110
CCCCCCCCCCC
C
C
C
C
C
APM C
C
C
C
C
C
0123 45 6789 10
0
1
2
3
4
5
6
7
8
9
10
00000000101
10010000111
11010000111
00000000101
11010000111
11011000111
11111101111
11111100111
00000000001
00000000101
00000000000
CCCCCCCCCCC
C
C
C
C
C
DPM C
C
C
C
C
C
Finally, the PSO method is applied for finding
the solutions. The test result is shown in Figure 4.
Figure 4 shows that the computation converges after
40 generations. After 150 generations, a solution
with the near optimized low cost of $302.968 can be
obtained. The numerical values of the position
matrix of the solution are shown in Figure 5. The
position matrix can be decoded to show the
integrated assembly and disassembly sequence.
Figure 6 describes the assembly and disassembly
sequence. The 11 components can be assembled and
disassembled with a near optimized low cost.
Cost (dollars) 302
Iterations (Generations) 150
Computer time (seconds) 1.281
Figure 4: The test result of the cost and generation number
of the PSO method.
ICSOFT 2010 - 5th International Conference on Software and Data Technologies
448

00 01 02 03 04 05 06 07 08 09 10
1.44 1.85 1.64 3.71 0.58 2.76 3.46 3.00 1.82 3.55 1.51
1.90 3.15 2.34 0.86 2.52 1.49 1.86 2.88 1.14 1.62 3.22
CCCCCCCCCCC
PM
Figure 5: The Numerical values of the position matrix of
the PSO solution.
Assembly
sequence
1 2 3 4 5 6 7 8 9 10 11
Component 7 2 5 6 4 1 0 9 8 3 10
Disassembly
sequence
1 2 3 4 5 6 7 8 9 10 11
Component 10 8 3 9 0 1 4 5 2 7 6
Figure 6: The final test results of the integrated assembly
and disassembly sequences.
It is observed that the combinatorial number of
sequences increases as the component number
grows. It can be concluded in general, the PSO
method can be considered an efficient and effective
method for find the solutions of integrated assembly
and disassembly sequences. Although the presented
methods can be useful for generating and evaluating
feasible sequences with good solutions, much
remains to be done to manage more complicated
products with a large number of components.
Further research on the complexity issues need to be
conducted.
6 CONCLUSIONS
In this research, a green decision support system is
presented to integrate assembly and disassembly
sequence planning models. First, graph-based
models are built by analyzing the spatial
relationships of the components and the operations.
Second, a solution method using a PSO approach is
applied to search for the good assembly sequence
and disassembly sequence. A new encoding scheme
of position matrix is developed for representing a
particle. A cost function by integrating the assembly
costs and disassembly costs is formulated. An
example product is illustrated in this paper. The test
results show that the PSO method converges within
a small number of generations with a near optimized
low cost. It can be generally concluded that the
developed model in the decision support system is
feasible and efficient for integrating assembly and
disassembly sequence planning. The green decision
support system is capable of finding complete
assembly and disassembly sequences with a near
optimized low cost. In further research, more
detailed assembly and disassembly cost functions
can be further explored. The solution method can be
refined to enhance the solution speed.
REFERENCES
Abdullah, T. A., Popplewell, K., and Page, C. J. (2003). A
review of the support tools for the process of assembly
method selection and assembly planning, International
Journal of Production Research, 41(11), pp. 2391–
2410.
Banks, A., Vincent, J., and Anyakoha, C. (2008). A review
of particle swarm optimization. Part II: hybridization,
combinatorial, multicriteria and constrained
optimization, and indicative applications, Natural
Computing, 7, 109-124.
Chen, R. S., Lu, K.-Y., and Tai, P. H. (2004). Optimizing
assembly planning through a three-stage integrated
approach, International Journal of Production
Economics, 88, pp. 243-256.
Gottipolu, R. B., and Ghosh, K. (1997). Representation
and selection of assembly sequences in computer-aided
assembly process planning, International Journal of
Production Research, 35(12), pp. 3447-3465.
Gungor, A., and Gupta, M. (2001). Disassembly sequence
plan generation using a branch-and-bound algorithm,
International Journal of Production Research, 39(1),
pp. 481-509.
Homem de Mello, L. S., and Sanderson, A. C. (1991).
Two criteria for the selection of assembly plans:
maximizing the flexibility of sequencing the assembly
tasks and minimizing the assembly time through
parallel execution of assembly tasks, IEEE Transactions
on Robotics and Automation, 7(5), pp. 626-633.
Huang, Y. M. and Huang, C. T. (2002). Disassembly
matrix for disassembly processed of products,
International Journal of Production Research, 40(2),
pp. 255- 273.
Kennedy, J., and Eberhart, R. C. (1997). A discrete binary
version of the particle swarm algorithm, Proceedings of
the International Conference on Systems, Man and
Cybernetics, Piscataway, NJ, 4104-4109.
Kongar, E., and Gupta, S. M. (2006). Disassembly
sequencing using genetic algorithm, International
Journal of Advanced Manufacturing Technology, 30,
pp. 497-506.
Lambert, A. J. D. (2003). Disassembly sequencing: a
survey, International Journal of Production Research,
41(16), pp. 3721- 3759.
Laperriere, L., and ElMaraghy, H. A. (1996). GAPP: A
Generative Assembly Process Planner, Journal of
Manufacturing Systems, 15(4), pp. 282-293.
Lin, A. C., and Chang, T. C. (1993). An integrated
approach to automated assembly planning for three-
dimensional mechanical products, International Journal
of Production Research, 31(5), pp. 1201-1227.
Torres, F., Puente, S. T., and Aracil, R. (2003).
Disassembly planning based on precedence relations
among assemblies, International Journal of Advanced
Manufacturing Technology, 21, pp. 317-327.
A GREEN DECISION SUPPORT SYSTEM FOR INTEGRATED ASSEMBLY AND DISASSEMBLY SEQUENCE
PLANNING USING A PSO APPROACH
449
