
TOWARDS A FASTER SYMBOLIC AGGREGATE
APPROXIMATION METHOD
Muhammad Marwan Muhammad Fuad and Pierre-François Marteau
VALORIA, Université de Bretagne Sud, Université Européenne de Bretagne, BP. 573, 56017, Vannes, France
Keywords: Time Series Information Retrieval, Symbolic Aggregate Approximation, Fast SAX.
Abstract: The similarity search problem is one of the main problems in time series data mining. Traditionally, this
problem was tackled by sequentially comparing the given query against all the time series in the database,
and returning all the time series that are within a predetermined threshold of that query. But the large size
and the high dimensionality of time series databases that are in use nowadays make that scenario inefficient.
There are many representation techniques that aim at reducing the dimensionality of time series so that the
search can be handled faster at a lower-dimensional space level. The symbolic aggregate approximation
(SAX) is one of the most competitive methods in the literature. In this paper we present a new method that
improves the performance of SAX by adding to it another exclusion condition that increases the exclusion
power. This method is based on using two representations of the time series: one of SAX and the other is
based on an optimal approximation of the time series. Pre-computed distances are calculated and stored
offline to be used online to exclude a wide range of the search space using two exclusion conditions. We
conduct experiments which show that the new method is faster than SAX.
1 INTRODUCTION
Similarity search is a hot topic in computer science.
This problem has many applications in multimedia
databases, bioinformatics, pattern recognition, text
mining, computer vision, and others. Small
structured databases can be handled easily. But
managing large unstructured, or weakly structured,
databases requires serious effort, especially when
they contain complex data types.
Time series are data types that appear in many
applications. Time series data mining includes many
tasks such as classification, clustering, similarity
search, motif discovery, anomaly detection, and
others. Research in time series data mining has
focussed on two aspects; the first aspect is the
dimensionality reduction techniques that can
represent the time series efficiently and effectively at
lower-dimensional spaces. Different indexing
structures are used to handle time series.
Time series are high dimensional data , so even
indexing structures can fail in handling these data
because of what is known as the “dimensionality
curse” phenomenon. One of the best solutions to
deal with this phenomenon is to utilize a
dimensionality reduction method to reduce the
dimensionality of the time series, then to use a
suitable indexing structure on the reduced space.
There have been different suggestions to
represent time series in lower dimensional spaces.
To mention a few; Discrete Fourier Transform
(DFT) (Agrawal et al . 1993) and (Agrawal et al.,
1995), Discrete Wavelet Transform (DWT) (Chan
and Fu 1999), Singular Value Decomposition
(SVD) (Korn et al., 1997), Adaptive Piecewise
Constant Approximation (APCA) (Keogh et al.,
2001), Piecewise Aggregate Approximation (PAA)
(Keogh et al., 2000) and (Yi and Faloutsos, 2000),
Piecewise Linear Approximation (PLA)
(Morinaka et al . 2001)
, Chebyshev Polynomials
(CP)
(Cai and Ng, 2004).
Among the different representation methods,
symbolic representation has several advantages,
because it allows researchers to benefit from text-
retrieval algorithms and techniques that are widely
used in the text mining and bioinformatics
communities (Keogh et al., 2001).
The other aspect of research in time series data
mining is similarity distances. There are quite a large
number of similarity distances; some of them are
305
Muhammad Fuad M. and Marteau P. (2010).
TOWARDS A FASTER SYMBOLIC AGGREGATE APPROXIMATION METHOD.
In Proceedings of the 5th International Conference on Software and Data Technologies, pages 305-310
DOI: 10.5220/0003006703050310
Copyright
c
SciTePress

applied to a particular data type, while others can be
applied to different data types.
Among the different similarity distances, there
are those that can be used on symbolic data types. At
first they were available for data types whose
representation is naturally symbolic (DNA and
proteins sequences, textual data…etc). But later
these symbolic similarity distances were extended to
apply to other data types that can be transformed
into sequences by using an appropriate symbolic
representation technique.
In time series data mining there are several
symbolic representation methods. Of all these
methods, the symbolic aggregate approximation
method (SAX) (Jessica et al . 2003) stands out as
one of the most powerful methods. The main feature
of this method is that the similarity distance that it
uses is easy to compute, because it uses statistical
lookup tables.
In this paper we present a new method that
speeds up SAX by adding a new exclusion condition
that increases the exclusion power of SAX. Our
method keeps the original features of SAX, mainly
its speed, since the new exclusion condition is pre-
computed offline.
The rest of this paper is organized as follows: in
section 2 we present background on dimensionality
reduction, and on symbolic representation of time
series in general, and SAX in particular. The
proposed method is presented in section 3. In section
4 we present some of the results of the different
experiments we conducted. The conclusion is
presented in section 5.
2 BACKGROUND
2.1 Representation Methods
Managing high-dimensional data is a difficult
problem in time series data mining. Representation
methods try to overcome this problem by embedding
the time series of the original space into a lower
dimensional space. Time series are highly correlated
data, so representation methods that aim at reducing
dimensionality by projecting the original data onto
lower dimensional spaces and processing the query
in those reduced spaces is a scheme that is widely
used in time series data mining community.
When embedding the original space into a lower
dimensional space and performing the similarity
query in the transformed space, two main side-
effects may be encountered; false alarms, also called
false positivity, and false dismissals. False alarms are
data objects that belong to the response set in the
transformed space, but do not belong to the response
set in the original space. False dismissals are data
objects that the search algorithm excluded in the
transformed space, although they are answers to the
query in the original space. Generally, false alarms
are more tolerated than false dismissals, because a
post-processing scan is usually performed on the
results of the query in the transformed space to filter
out these data objects that are not valid answers to
the query in the original space. However, false
alarms can slow down the search time if the
algorithm returns too many of them. False dismissals
are a more serious problem and they need more
sophisticated procedures to avoid them.
False alarms and false dismissals are dependent on
the transformation used in the embedding. If
f is a
transformation from the original space
),(
origorig
dS
into another space ),(
transtrans
dS then
in order to guarantee no false dismissals this
transform should satisfy:
),())(),((
2121
uudufufd
origtrans
≤
orig
Suu ∈∀
21
,
(1)
The above condition is known as the lower-
bounding lemma.
(Yi and Faloutsos 2000)
If a transformation can make the two above
distances equal for all the data objects in the original
space, then similarity search produces no false
alarms or false dismissals. Unfortunately, such an
ideal transformation is very hard to find. Yet, we try
to make the above distances as close as possible.
The above condition can be written as:
1
),(
))(),((
0
21
21
≤≤
uud
ufufd
orig
trans
(2)
A tight transformation is one that makes the above
ratio as close as possible to 1.
2.2 SAX
Symbolic representation of time series has attracted
much attention recently, because by using this
method we can not only reduce the dimensionality
of time series, but also benefit from the numerous
algorithms used in bioinformatics and text data
mining. However, first symbolic representation
methods were ad hoc and did not give satisfactory
results. But later more sophisticated methods
emerged. Of all these method, the symbolic
aggregate approximation method (SAX) is one of
the most powerful ones in time series data mining.
ICSOFT 2010 - 5th International Conference on Software and Data Technologies
306
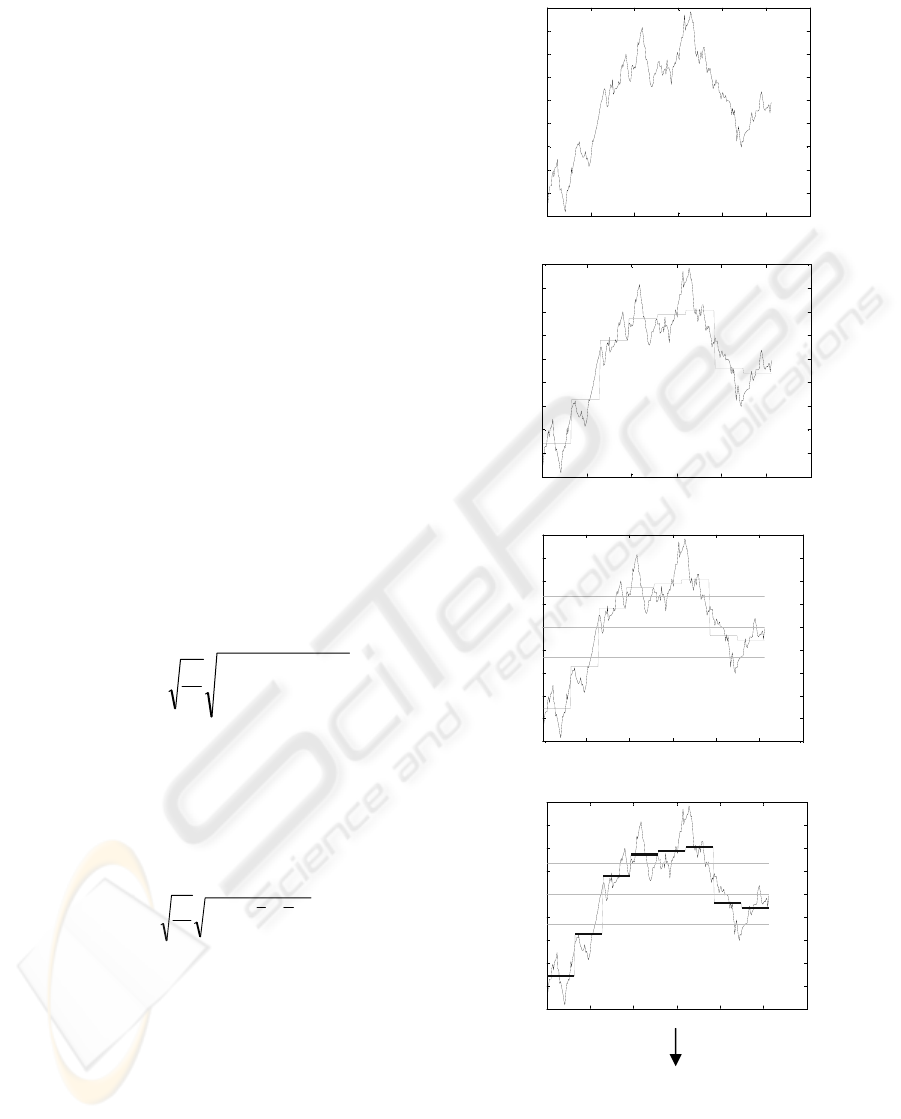
SAX is based on the fact that normalized time series
have highly Gaussian distribution (Larsen and Marx
1986), so by determining the breakpoints that
correspond to the chosen alphabet size, one can
obtain equal sized areas under the Gaussian curve.
SAX is applied in the following steps: in the first
step all the time series in the database are
normalized. In the second step, the dimensionality of
the time series is reduced by using the PAA. In PAA
the times series is divided into equal sized segments
or “frames” and the mean value of the points that lie
within the frame is computed. The lower
dimensional vector of the original time series is the
vector whose components are the means of all
successive frames of the time series. In the third
step, the PAA representation of the time series is
discretized. This is achieved by determining the
number and the location of the breakpoints. This
number is related to the desired alphabet size (which
is chosen by the user), i.e.
alphabet_size=number(breakpoints)+1 . Their
locations are determined by statistical lookup tables,
so that these breakpoints produce equal-sized areas
under the Gaussian curve. The interval between two
successive breakpoints is assigned to a symbol of the
alphabet, and each segment of the PAA that lies
within that interval is discretized by that symbol.
The last step of SAX is using the following
similarity distance:
2
1
))
~
,
~
(()
~
,
~
(
∑
=
≡
N
i
ii
tsdist
N
n
TSMINDIST
(3)
Where
n is the length of the original time series, N is
the number of the frames,
S
~
and
T
~
are the symbolic
representations of the two time series
S and
T
,
respectively, and where the function
(
)
dist is
implemented by using the appropriate lookup table.
We need to mention that the similarity distance
used in PAA is:
∑
=
−=
N
i
yx
N
n
YXd
1
2
)(),(
(4)
Where n is the length of the time series, N is the
number of frames. It is proven in
(Keogh, et al. 2000)
and (Yi and Faloutsos 2000) that the above
similarity distance is a lower bounding of the
Euclidean distance applied in the original space of
time series . This results in the fact that MINDIST is
also a lower bounding of the Euclidean distance,
because it is a lower bounding of the similarity
distance used in PAA. This guarantees no false
dismissals. Figure.1 illustrates the different steps of
SAX.
(1)The original time series.
0 50 100 150 200 250 300
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
(2) Converting the time series to PAA.
0 50 100 150 200 250 300
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
(3) Choosing the breakpoints.
0 50 100 150 200 250 300
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
(4) Discretizing PAA.
0 50 100 150 200 250 300
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
a
a
c
d
d
d
b
b
aacdddbb
Figure 1: The different steps of applying SAX.
TOWARDS A FASTER SYMBOLIC AGGREGATE APPROXIMATION METHOD
307

3 THE PROPSED METHOD
The basis of our method is to improve the
performance of SAX by combining it with an
exclusion condition that increases its pruning power,
and by using different reduced spaces, and not only
one.
We divide each time series into
N
segments.
Each segment is approximated by a polynomial. In
this paper we use a polynomial of the first-degree for
its simplicity, but other approximating functions can
be used as well.
Since this approximating function is the optimal
approximation of the corresponding segment, the
distance between this segment and this
approximating function is minimal. The time series
is also represented using SAX in the way indicated
in section 2.2. A polynomial of the same degree is
used to approximate all the segments of all the time
series in the database. So now each time series has
two representations: the first is a
n-dimensional
one, by using the approximating function, and the
second is a
N
-dimensional one, by using SAX. We
also have two similarity distances; the first one is the
Euclidean distance, which is the distance between a
time series and its approximating function, and the
other one is MINDIST, which is the distance in the
reduced space.
Given a query
),(
ε
q , let u , q be the projections
of the
u , q , respectively, on their approximating
functions, where
u
is a time series in the database.
By applying the triangular inequality we get:
),(),(),( qqduqduqd +≤ (5)
Taking into consideration that
u is the best
approximation of u , we get:
),(),( quduud ≤ (6)
By substituting the above relation in (5), we can
safely exclude all the times series that satisfy:
),(),( qqduud +>
ε
(7)
In a similar manner, and since
q
is the best
approximation of
q , we can safely exclude all the
time series that satisfy:
),(),( uudqqd +>
ε
(8)
Both (7), (8) can be expressed in one relation:
ε
>− ),(),( qqduud (9)
In addition to the exclusion condition in (9), since
MINDIST is lower bounding of the original
Euclidean distance, all the time series that satisfy:
ε
>),( uqMINDIST (10)
Should also be excluded, Relation (10) defines the
other exclusion condition.
The Offline Phase. The application of our method
starts by choosing the lengths of segments. We
associate each length with a level of representation.
The shortest lengths correspond to the lowest level,
and the longest lengths with the highest levels. Each
series in the database is represented by a first-degree
polynomial, which is the same approximating
function for all the time series in the databases. The
distances between the time series and their
approximating function are computed and stored. In
order to represent the time series, we choose the
alphabet size to be used. SAX appeared in two
versions; in the first one the alphabet size varied in
the interval (3:10), and in the second one the
alphabet size varied in the interval (3:20). We
choose the appropriate alphabet size for this
datasets. The time series in the database are
represented using SAX on every representation level
The Online Phase. The range query is represented
using the same scheme that was used to represent the
time series in the database. We start with the lowest
level and try to exclude the first time series using (9)
if this time series is excluded, we move to the next
time series, if not, we try to exclude this time series
using relation (10). If all the time series in the
database have been excluded the algorithm
terminates, if not, we move to a higher level. Finally,
after all levels have been exploited, we get a
potential answer set, which is linearly scanned to
filter out all the false alarms and get the true answer
set.
4 EXPERIMENTS
We conducted experiments on different datasets
available at UCR (UCR Time Series datasets) and
for all alphabet sizes, which vary between 3 (the
least possible size that was used to test the original
SAX) to 20 (the largest possible alphabet size). We
compared the speed of our method FAST_SAX,
with that of SAX as a standalone method. The
comparison was based on the number of operations
that each method uses to perform the similarity
search query. Since different operations take
different execution times, we used the concept of
latency time (Schulte et al. 2005). We report in
Tables 1 and in Figure 2 the results of (wafer). We
chose to present the results of this dataset because it
is the largest dataset in the repository. Also it is
shown in (Muhammad Fuad and Marteau 2008) that
the best results obtained with SAX were with this
dataset.
ICSOFT 2010 - 5th International Conference on Software and Data Technologies
308

The codes of SAX were optimized versions of the
original codes, since the original codes were not
optimized for speed
Table 1: Comparison of the latency time between SAX
and FAST_SAX for ε=1:4 and alphabet size=3, 10, 20.
α= 3 α= 10 α= 20
FAST_SAX
1.0592E6 3.7136E5
2.6734E5
SAX 5.1291E6 1.5764E6 1.2759E6
ε=1
(a)
α= 3 α= 10 α= 20
FAST_SAX
7.2062E6 3.3509E6
2.2255E6
SAX 1.567E7 4.8078E6 3.4253E6
ε=2
(b)
α= 3 α= 10 α= 20
FAST_SAX
1.3717E7 1.1444E7
9.5446E6
SAX 2.1944E7 1.4428E7 1.1144E7
ε=3
(c)
α= 3 α= 10 α= 20
FAST_SAX
2.2697E7 1.6928E7
1.6611E7
SAX 2.8287E7 2.2179E7 1.9877E7
ε=4
(d)
The results of testing our method on other datasets
are similar to the results obtained with (wafer)
The results shown here are for alphabet size 3
(the smallest alphabet size), 10 (the largest alphabet
size in the first version of SAX), and 20 (the largest
alphabet size in the second version of SAX)
The results obtained show that FAST_SAX
outperforms SAX for the different values of ε and
for the different values of the alphabet size.
5 CONCLUSIONS
AND PERSPECTIVES
In this paper we presented a method that speeds up
the symbolic aggregate approximation (SAX). We
conducted several experiments of times series
similarity search, with different values of the
alphabet size and different threshold values. The
results obtained show that the new method is faster
than the original SAX
1 2 3 4
0
0.5
1
1.5
2
2.5
3
x 10
7
ε
Latency Time
FAST SAX
SAX
(a)
1 2 3 4
0
0.5
1
1.5
2
2.5
x 10
7
ε
Latency Time
FAST SAX
SAX
(b)
1 2 3 4
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
x 10
7
ε
Latency Time
FAST SAX
SAX
(c)
Figure 2: Comparison of the latency time between SAX
and FAST_SAX for alphabet size=3 (a), alphabet size=10
(b) and alphabet size=20 (c).
The future work can focus on extending this method
to other representation methods, other than SAX,
also on using other approximating functions.
REFERENCES
Agrawal, R., Faloutsos, C., & Swami, A. 1993: Efficient
Similarity Search in Sequence Databases. Proceedings
of the 4th Conf. on Foundations of Data Organization
and Algorithms.
TOWARDS A FASTER SYMBOLIC AGGREGATE APPROXIMATION METHOD
309

Agrawal, R., Lin, K. I., Sawhney, H. S. and Shim. 1995:
Fast Similarity Search in the Presence of Noise,
Scaling, and Translation in Time-series Databases, in
Proceedings of the 21st Int'l Conference on Very
Large Databases. Zurich, Switzerland, pp. 490-501.
Cai, Y. and Ng, R. 2004: Indexing Spatio-temporal
Trajectories with Chebyshev Polynomials. In
SIGMOD.
Chan, K. & Fu, A. W. 1999: Efficient Time Series
Matching by Wavelets. In proc. of the 15th IEEE Int'l
Conf. on Data Engineering. Sydney, Australia, Mar
23-26. pp 126-133..
Jessica Lin, Eamonn J. Keogh, Stefano Lonardi, Bill
Yuan-chi Chiu. 2003: A Symbolic Representation of
Time Series, with Implications for Streaming
Algorithms. DMKD 2003: 2-11.
Keogh, E,. Chakrabarti, K,. Pazzani, M. & Mehrotra.
2000: Dimensionality Reduction for Fast Similarity
Search in Large Time Series Databases. J. of Know.
and Inform. Sys.
Keogh, E,. Chakrabarti, K,. Pazzani, M. & Mehrotra.
2001: Locally Adaptive Dimensionality Reduction for
Similarity Search in Large Time Series Databases.
SIGMOD pp 151-162 .
Korn, F., Jagadish, H & Faloutsos. C. 1997: Efficiently
Supporting ad hoc Queries in Large Datasets of Time
Sequences. Proceedings of SIGMOD '97, Tucson, AZ,
pp 289-300.
Larsen, R. J. & Marx, M. L. 1986. An Introduction to
Mathematical Statistics and Its Applications. Prentice
Hall, Englewood, Cliffs, N.J. 2nd Edition.
Morinaka, Y., Yoshikawa, M. , Amagasa, T., and
Uemura, S 2001: The L-index: An Indexing Structure
for Efficient Subsequence Matching in Time Sequence
Databases. In Proc. 5th PacificAisa Conf. on
Knowledge Discovery and Data Mining, pages 51-60 .
Muhammad Fuad, M.M. and Marteau, P.F. 2008: The
Extended Edit Distance Metric, Sixth International
Workshop on Content-Based Multimedia Indexing
(CBMI 2008) 18-20th June, 2008, London, UK.
Schulte,M. J. ,Lindberg, M. and Laxminarain, A. 2005:
Performance Evaluation of Decimal Floating-point
Arithmetic in IBM Austin Center for Advanced
Studies Conference, February
Yi, B. K., & Faloutsos, C. 2000: Fast Time Sequence
Indexing for Arbitrary Lp norms. Proceedings of the
26st International Conference on Very Large
Databases, Cairo, Egypt .
UCR Time Series datasets
http://www.cs.ucr.edu/eamonn/time_series_data/
ICSOFT 2010 - 5th International Conference on Software and Data Technologies
310
