MINING TIMED SEQUENCES TO FIND SIGNATURES

Nabil Benayadi and Marc Le Goc

LSIS Laboratory, University Saint Jerome, Marseille, France

Keywords:

Information-theory, Temporal knowledge discovering, Chronicles models, Markov processes.

Abstract:

We introduce the problem of mining sequential patterns among timed messages in large database of sequences

using a Stochastic Approach. An example of patterns we are interested in is : 50% of cases of engine stops

in the car are happened between 0 and 2 minutes after observing a lack of the gas in the engine, produced

between 0 and 1 minutes after the fuel tank is empty. We call this patterns “signatures”. Previous research

have considered some equivalent patterns, but such work have three mains problems : (1) the sensibility of

their algorithms with the value of their parameters, (2) too large number of discovered patterns, and (3) their

discovered patterns consider only ”after“ relation (succession in time) and omit temporal constraints between

elements in patterns. To address this issue, we present TOM4L process (Timed Observations Mining for

Learning process) which uses a stochastic representation of a given set of sequences on which an inductive

reasoning coupled with an abductive reasoning is applied to reduce the space search. A very simple example

is used to show the efﬁciency of the TOM4L process against others literature approaches.

1 INTRODUCTION

A ”MonitoringCognitiveAgent” (MCA) is a software

system that aims at monitoring, diagnosing and con-

trolling dynamic processes like manufacturing pro-

cesses, telecommunication networks or web servers.

The main task of an MCA is to analyze the sensor

data provided by the instrumentation to inform about

the observed behavior of the process with timed mes-

sages. Huge amounts of timed messages so collected

in temporal databases (so-called ”event log”). There

is an increasing interest in mining these timed mes-

sages to discover patterns that describe relations be-

tween the variables that govern the dynamic of the

process and so improving its management.

In this paper, we introduce the problems of mining

such a pattern: 50% of cases of engine stops in the car

are happen between 0 and 2 minutes after observing a

lack of the gas in the engine, produced between 0 and

1 minutes after the fuel tank is empty. We call this pat-

terns “signatures”. Finding signatures are valuable in

many ﬁelds, for example, when targeting markets us-

ing DM (Direct Mail), market analysts can use signa-

tures to learn what actions they should take and when

they should act to inform their customers to buy. We

propose in this paper the basis of the TOM4L pro-

cess (Timed Observations Mining for Learning pro-

cess) deﬁned to discover signatures among timed

messages in large database of sequences. TOM4L

process avoids also the two remains problems of

Timed Data Mining techniques: the sensitivity of the

Timed Data Mining algorithms with the value of their

parameters and the too large number of generated pat-

terns. TOM4L avoids these two problems with the

use of a stochastic representation of a given set of

sequences on which an inductive reasoning coupled

with an abductive reasoning is applied to reduce the

space search. In the literature, the common charac-

teristic of techniques that mine sequences is the dis-

covery of patterns that are frequents (Agrawal and

Srikant, 1995), (Mannila et al., 1997): the more fre-

quently a pattern occurs, the more likely a pattern is

important. Mining sequential patterns was originally

proposed for market analysis (Agrawal and Srikant,

1995) where the temporal relations between retail

transactions are mined with the AprioriAll algorithm.

This algorithm is based on a interestingness criteria

called the ”support” of a sequential pattern, deﬁned as

the number of time a pattern is observed at least one

time in a sequence. A pattern is then frequent when

its support is greater than a given arbitrary threshold.

Because this approach fails when there is only one

sequence, two principal solutions have been proposed

to gets around of this problem: the Maximal window

size constraint solution and the minimal occurrence

solution (Mannila et al., 1997). The Maximal win-

450

Benayadi N. and Le Goc M. (2010).

MINING TIMED SEQUENCES TO FIND SIGNATURES.

In Proceedings of the 5th International Conference on Software and Data Technologies, pages 450-455

DOI: 10.5220/0003007604500455

 SciTePress

dow size constraint solution devises the sequence in

set of sub-sequences so that a support can be com-

puted (Winepi algorithm). Because the cutting of the

sequence is arbitrary, Minepi algorithm is proposed

that uses the minimal occurrences solution to deﬁne

the windows. The problem with these ”Frequential

Approaches” is that the support allows to discover a

lot of frequently observed patterns that are not rep-

resentative of the relations between the process vari-

ables. So ”informativeness” criteria are required to

reduce the set of frequent patterns. The Stochastic

Approach proposes to reverse this sequence mining

process to ﬁrst identify the potential interesting pat-

terns before looking for frequently observed patterns.

The next section presents a simple illustrative ex-

ample to show the main problems of previous ap-

proaches. Section 3 introduces the basis of the

TOM4L process and the section 4 discusses and com-

pares the results obtained by TOM4L process and oth-

ers literature approaches on the illustrative example.

The section 5 makes a synthesis of the paper and in-

troduces our current works.

2 ILLUSTRATIVE EXAMPLE

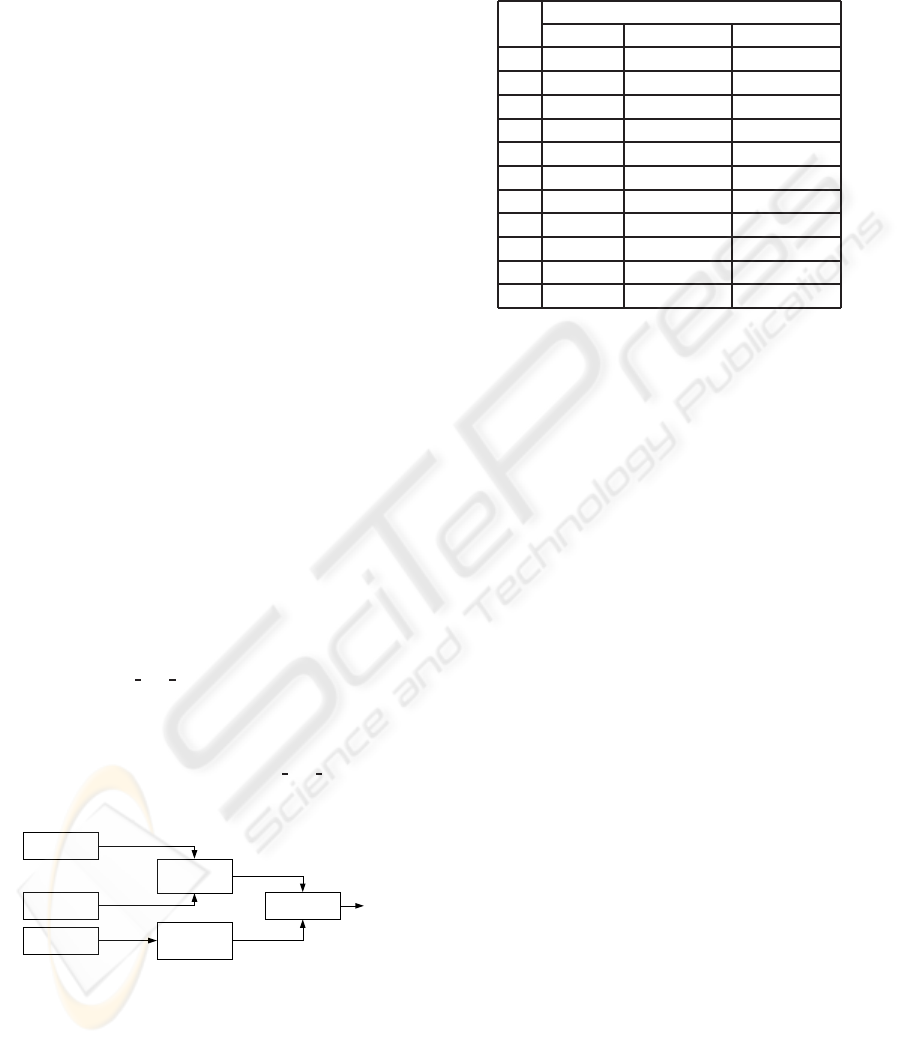
Consider a system that monitors the stopping problem

of a car. Figure 1 shows the structure of the monitored

variables that might affect the stopping of a car. There

are 6 variables (x1,x2,x3,x7,x8,x9) in the car system

that can be assigned to following constants: ∆= {x1 =

{Blown},x2 = {Low},x3 = {Empty},x7 = {Of f },x8 =

{False},x9 = {Does Not Start}}.

Let suppose that the car system was moni-

tored for 30 minutes, this leads to the following

sequence of 100 observations :

= (Low,t

(Empty,t

),(Empty,t

),(False,t

),(Does Not Start,t

·· ·, (O f f,t

), (Empty,t

), (Low,t

100

)}.

electric_

alimentation

gas_

alimentation

engine

fuse

battery

fuel_tank

x1t 

x2t 

x3 t 

x8 t 

x9 t 

x7 t 

Figure 1: Temporal evolution of variables.

To illustrate the sensibility of the ApprioriAll,

Winepi and the Minepi algorithms with the parame-

ters, we deﬁnes a set of parameters and apply the al-

gorithms to the sequence

. The window widths W

are set from 2 to 12, and for every window width W,

the window movement v is set to W/3.

The table 1 provides the number of patterns dis-

covered by each algorithm with the set of parameters.

Table 1: Number of discovered patterns.

Number of the discovered patterns

Winepi AprioriAll Minepi

2 16 16 27

3 28 28 41

4 51 51 57

5 79 79 74

6 133 133 111

7 211 211 145

8 293 293 197

9 282 282 256

10 381 381 329

11 494 494 464

12 825 825 593

These experimentationsshowthe sensibility of the

Winepi, AprioriAll and the Minepi algorithms with

the parameters: from the ﬁrst to the end experimen-

tation, the number of patterns increase of more than

5156% for Winepi and AprioriAll, and more than

21961% from Minepi. The main problem is the too

large number of discovered patterns. The paradox is

then the following: to ﬁnd the ideal set of parameters

that minimizes the number of discovered patterns, the

user must know the system while this is precisely the

global aim of the Data Mining techniques. There is

then a crucial need for another type of approach that is

able to provide a good solution for such a simple sys-

tem and provide operational solutions for real world

systems. The aim of this paper is to propose such an

approach: the TOM4L process which ﬁnd only 3 re-

lations with the example without any parameters.

3 STOCHASTIC APPROACH

FRAMEWORK

The TOM4L process is based on the Theory of Timed

Observations of (Le Goc, 2006) that deﬁnes an in-

ductive reasoning and an abductive reasoning on a

stochastic representation of a set of sequences Ω =

{

}, this set not necessarily a singleton. This theory

provides the mathematical foundations of four steps

that reverses the usual Data Mining process in order

to minimize the size of the set of the discovered pat-

terns.

Basic Deﬁnitions

A discrete event e

is a couple (x

) where x

the name of a variable and

is a constant. The

MINING TIMED SEQUENCES TO FIND SIGNATURES

451

constant

denotes an abstract value that can be

assigned to the variable x

. The illustrative exam-

ple allows the deﬁnition of a set E of six discrete

events: E = {e

≡ (x1, Blown), e

≡ (x2, Low), e

≡

(x3,Empty), e

≡ (x7,Of f), e

≡ (x8,False), e

≡

(x9,Does Not Start)}. A discrete event class C

} is an arbitrary set of discrete event e

= (x

Generally, the discrete event classes are deﬁned as

singletons because when the constants

are inde-

pendent, two discrete event classes C

= {(x

)}

and C

= {(x

)} are only linked with the vari-

ables x

and x

(Le Goc, 2006). The illustrative ex-

ample allows the deﬁnition of a set Cl of 6 discrete

event classes: Cl = {C

= {e

}, C

= {e

}, C

= {e

}, C

= {e

}, C

= {e

}}.

An occurrence o(k) of a discrete event classC

= {e

= (x

), is a triple (x

) where t

is the time

of the occurrence. When useful, the rewriting rule

o(k) ≡ (x

) ≡ C

(k) will be used in the follow-

ing. A sequence Ω = {o(k)}

k=1...n

, is an ordered

set of n occurrences C

(k) ≡ (x

). For exam-

ple, the illustrative example deﬁnes the following se-

quence: Ω = {(C

(1), C

(2), C

(3), C

(4), C

(5), ··· ,

(98), C

(99), C

(100)}. When the constants

∈ ∆

are independent, a sequence Ω = {o(k)} deﬁning a

set Cl = {C

} of m classes is the superposition of m

sequences

= {C

(k)} (Le Goc, 2006):

Ω = {o(k)} =

[

i=1...m

= {C

(k)} (1)

Where each sequence

= {C

(k)} contains only the

observations of the same class C

. For example, the Ω

sequence of the illustrative example is then the super-

position of six sequences

= {C

(k)}.

3.1 Step 1: Stochastic Representation

The stochastic representation transforms a set of se-

quences Ω in a Markov chain X = (X(t

);k > 0)

where the state space Q = {q

}, i = 1...m, of X is

confused with the set of m classes Cl = {C

} of Ω.

Consequently, two successive occurrences (C

(k− 1),

(k)) correspond to a state transition in X: X(t

k−1

) =

−→ X(t

) = q

. The conditional probability

P[X(t

) = q

|X(t

k−1

) = q

] of the transition from a

state q

to a state q

in X corresponds then to the

conditional probability P



(k) ∈ Ω|C

(k− 1) ∈ Ω



of observing an occurrence of the class C

at time t

knowing that an occurrence of a class C

at time t

k−1

has been observed:

∀i, j, ∀k ∈ K,



X(t

) = q

|X(t

k−1

) = q





(k) ∈ Ω|C

(k− 1) ∈ Ω



≡ p

∑

l,l6=i

The transition probability matrix P = [p

i, j

] of X

is computed from the contingency table N = [n

i, j

where n

i, j

∈ N is the number of couples (C

(k),C

(k+

1)) in Ω. The stochastic representation of a given

set Ω of sequences is then the deﬁnition of a set

R = {R

i, j

−

])} where each the condi-

tional probability p

i, j

= P



(k) ∈ Ω|C

(k− 1) ∈ Ω



of each binary relation R

i, j

−

]) is not

null. The timed constrains [

−

] is provided by a

function of the set D of delays D = {d

} = {(t

−

)} computed from the binary superposition of the

sequences

i, j

∪

−

= f

−

(D),

= f

(D).

For example, the authors of (Le Goc, 2006) use the

properties of the Poisson law to compute the timed

constraints:

−

= 0,

i, j

where

i, j

is the Pois-

son rate (i.e. the exponential intensity) of the expo-

nential law that is the average delay d

moy

∑

)

Card(D)

The set R of the illustrative example is a set of 26

binary relations : R = {R

i, j

−

i, j

])} where

i, j

> 0.

3.2 Step 2: Induction of Binary

Relations

Considering a binary relation R

i, j

−

]), a

sequence Ω deﬁning the set Cl of m classes with n

occurrences contains n − 1 couples (o(k), o(k + 1)).

Each of them is one of the four following types:

(k),C

(k + 1)), (C

(k),C

(k + 1)), (C

(k),C

(k +

1)), and (C

(k),C

(k + 1)), where C

(resp. C

) is

an abstract class denoting any classes of Cl except

(resp. C

). The n − 1 couples (o(k),o(k + 1))

can then be seen as n− 1 realizations of one of the

four relations linking two abstract binary variables X

and Y of a discrete binary memoryless channel in a

communication system according to the information

theory (Shannon, 1949), where X(t

) ∈ {C

} and

Y(t

k+1

) ∈ {C

} (Figure 2). To use this model, the

Figure 2: Two abstract binary variables connected by a dis-

crete memoryless channel.

ICSOFT 2010 - 5th International Conference on Software and Data Technologies

452

number of occurrences of the abstract classes C

and

can not be the number of the occurrences of the

classes Cl −C

and Cl −C

but an average value:

• n

i, j

is the number of couples (C

(k),C

(k+ 1)) in

Ω.

• n

i, j

is the average number of couples

(k),C

(k+ 1)) in Ω:

• n

i, j

m− 1

∑

∀C

∈C

i,l

• n

i, j

is the average number of couples

(k),C

(k+ 1)) in Ω:

• n

i, j

m− 1

∑

∀C

∈C

l, j

• n

i, j

is the average number of couples

(k),C

(k+ 1)) in Ω:

• n

i, j

(m− 1)

∑

∀C

∈C

,∀C

∈C

l, f

This leads to m·(m−1) binary contingency tables

of the form of the Table 2.

Table 2: Contingency table for X and Y.

∑

i, j

∑

y∈{ j, j}

i,y

i, j

∑

y∈{ j, j}

i,y

∑

x∈{i,i}

x, j

∑

x∈{i,i}

x, j

N =

∑

x∈{i,i},y∈{ j, j}

x,y

These contingency tables allow computing

two conditional probabilities matrix P

(i.e.

P(Y(t

k+1

)|X(t

))) and P

(i.e. P(X(t

)|Y(t

k+1

)).

These two matrix allow the deﬁnition of the BJ-

measure to build a criterion to evaluate the interest of

a binary relation R

i, j

−

]).

3.2.1 Interestingness of Binary Relations

The idea for deﬁning an efﬁcient interestingness

criterion to induce binary relations is that if know-

ing C

(k) increases the probability of observing

(k + 1) (i.e. p(C

) > p(C

)), then the ob-

servation C

(k) provides some information about

an observation C

(k + 1) (Blachman, 1968). We

propose then to use the distance of Kullback-Leibler

D(p(Y|X = C

)kp(Y)) to evaluate the relation

between the a priori distribution p(C

) of an observa-

tion C

(k) and the conditional distribution p(C

D(p(Y |X = C

)kp(Y)) =

p(Y = C

|X = C

) ×log



p(Y=C

|X=C

)

p(Y=C

)



p(Y = C

|X = C

) ×log



p(Y=C

|X=C

)

p(Y=C

)



(2)

In order to remove the symmetry introduced when

evaluating the relation R

i, j

) and R

i, j

) ,

we propose to use an oriented Kullback-Leibler dis-

tance, called BJL.

Deﬁnition 1. The BJL-measure BJL(C

) of binary

relation R(C

) is the right part of the Kullback-

Leibler distance D(p(Y|X = C

)kp(Y)):

• p(Y = C

|X = C

) < p(Y = C

) ⇒ BJL(C

) =

• p(Y = C

|X = C

) ≥ p(Y = C

) ⇒ BJL(C

) =

D(p(Y|X = C

)kp(Y))

The BJL(C

) is the information brought by the

occurrences of the class C

about the occurrences of

the class C

. The Kullback-Leibler distance can be

written as the sum of two BJL as follow:

D(p(Y|C

)kp(Y)) = BJL(C

) + BJL(C

) (3)

Contrary to Kullback-Leibler distance,

BJL(C

) is an asymmetric measure which

differently evaluates the binary relations R

i, j

)

and R

i, j

) . The same reasoning can be done

when considering the information distribution be-

tween the predecessors X(t

) = C

or X(t

) = C

the assignation Y(t

k+1

) = C

Deﬁnition 2. The BJW-measure BJW(C

) of

binary relation R(C

) is the right part of the

Kullback-Leibler distance D(p(X|Y = C

)kp(X)):

• p(X = C

|Y = C

) < p(X = C

) ⇒ BJW(C

) =

• p(X = C

|Y = C

) ≥ p(X = C

) ⇒ BJW(C

) =

D(p(X|Y = C

)kp(X))

Both the BJL(C

) and BJW(C

) measures

are combined in a single measure called BJM(C

Deﬁnition 3. The BJM-measure BJM(C

) of a

binary relation R(C

) is the norm of the vector



BJL(C

)

BJW(C

)



• (p(C

) ≥ p(C

)) ∨ (p(C

) ≥ p(C

)) ⇒

BJM(C

) =

BJL(C

)

+ BJW(C

)

• (p(C

) < p(C

)) ∨ (p(C

) < p(C

)) ⇒

BJM(C

) = −

BJL(C

)

+ BJW(C

)

MINING TIMED SEQUENCES TO FIND SIGNATURES

453

The minus sign is used to build a monotonous

measure that distinguishes the position of a relation

R(C

) around the independence point. The BJM-

measure BJM(C

) of a relation R(C

) is then

simply:

BJM(C

) =

BJL(C

)

+ BJW(C

)

−

BJL(C

)

+ BJW(C

)

The maximum value BJM(C

)

max

(obtained

when n

i, j

= min(n

,nj)) and the minimum value of

BJM(C

)

min

(obtained when n

i, j

= 0) depend on

the ratio

i, j

. The comparison of two BJM-

measures is not possible. To avoid this problem, the

BJM-measure BJM(C

) is made linear with a M-

measure M(C

) deﬁned as follows:

Deﬁnition 4.

M(C

) =











BJM(C

)

BJM(C

)

max

if p(C

) > p(C

)

−

BJM(C

)

BJM(C

)

min

else

Whatever is the ratio

i, j

, the M-measure M(C

)

as the following properties:

• M(C

) = 1 ⇔ BJM(C

) = BJM(C

)

max

(ideal crisscross)

• M(C

) = 0,5 ⇔ BJM(C

) = 0 (C

and C

are independent)

• M(C

) = 0 ⇔ BJM(C

) = BJM(C

)

min

and C

are not linked)

For example, the values of the M-measure of the 26

binary relations of R of the illustrative example are

given in table 3. The measure M can ﬁnally used as

Table 3: Matrix M.

M C

0.56 0 0 0.8 0 0

0 0 0 0.64 0 0

0 0.52 0.49 0 0.54 0

0 0 0.501 0 0 0.59

0 0.501 0.51 0 0 0.59

0 0.51 0.54 0 0.51 0

interestingness criterion for inducing binary relations

as follows :

M(C

) > 0.5 ⇒ R

i, j

) ∈ I (4)

For example, the set I of binary relations that

can be induced from R of the illustrative ex-

ample contains 13 binary relations : I =

{R(C

−

1,1

]),R(C

−

1,7

]),·· · }.

3.3 Step 3: Deduction of n-ary Relations

The set I of binary relations contains then the minimal

subset of R where each relation R

i, j

) presents

a potential interest. From this set, we can build a

set of n-ary relations having some potential to be ob-

served in the initial set Ω of sequences. To this aim,

an heuristic h(m

i,n

) can be used to guide an abduc-

tive reasoning to build a minimal set M = {m

k,n

} of

n-ary relations of the form m

k,n

= {R

i,i+1

i+1

)},

i = k, · · · ,n− 1, that is to say paths leading to a partic-

ular ﬁnal observation class C

. The heuristic h(m

i,n

)

makes a compromise between the generality and the

quality of a path m

i,n

h(m

i,n

) = card(m

i,n

) × BJL(m

i,n

) × P(m

i,n

) (5)

In this equation, card(m

i,n

) is the number of relations

in m

i,n

, BJL(m

i,n

) is the sum of the BJL-measures

BJL(C

k−1

) of each relation R

k−1,k

k−1

) in

i,n

and P(m

i,n

) corresponds to the Chapmann-

Kolmogorovprobability of a path in the transition ma-

trix P = [p(k−1,k)] of the Stochastic Representation.

The interestingness heuristic h(m

i,n

) being of the form

· ln(

), it can be used to build all the paths m

i,n

where h(m

i,n

) is maximum (Benayadi and Le Goc,

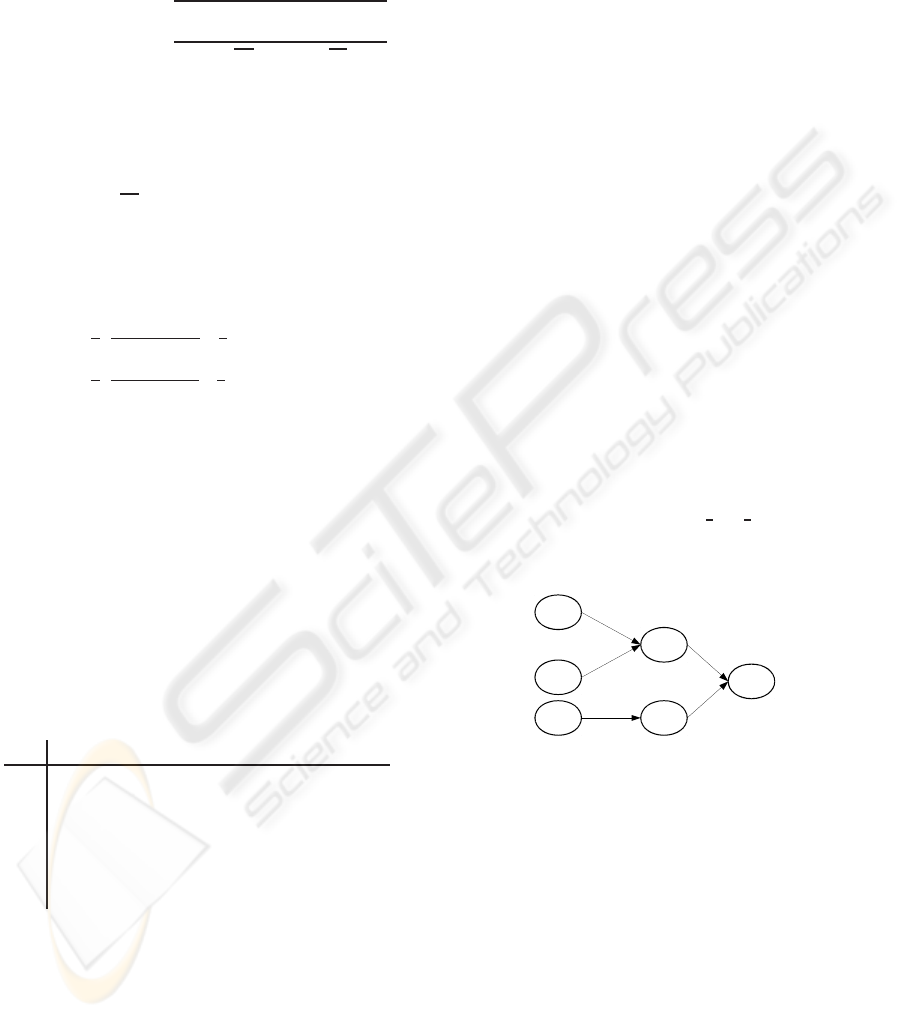
2008a). For the illustrative example, let suppose that

we are interested by explaining observations of the

class C

= {e

≡ (x9,Does Not Start)}). So, the

deduction step found three n-ary relations leading to

the class C

(Figure 3).

[

7,9



, 

7,9



]

[

8,9



, 

8,9



]

[

3,8



, 

3,8



]

[

2,7



,

2,7



]

[

1,7



, 

1,7



]

Fuse= blown

Battery= low

Power= off

Gas in Engine= false

Engine behavior =does not start , stops

Fuel Tank =empty

Figure 3: The discovered three n-ary relations.

3.4 Step 4: Find Representativeness

n-ary Relations

Given a set M = {m

k,n

)} of paths m

k,n

i,i+1

i+1

)}, i = k,·· · ,n − 1, the TOM4L

process uses two representativeness criteria to build

the subset S ⊆ M containing the only paths m

k,n

being representative according the initial set Ω of

sequences. These criteria are a timed version of

support and conﬁdence notions:

Deﬁnition 5. Anticipation Rate. The anticipation

rate Ta(m

i,n

) of a n-ary relation m

i,n

is the ratio

between the number of instances of m

i,n

in Ω with

ICSOFT 2010 - 5th International Conference on Software and Data Technologies

454

the number of occurrences of the m

i,n−1

(i.e. the

n-ary relation m

i,n

without the last binary relation

n−1,n

n−1

)).

Deﬁnition 6. Cover Rate. The cover rate Tc(m

i,n

) of

a n-ary relation m

i,n

is the ratio between the number

of occurrences of m

i,n

with the number of occurrences

of the ﬁnal class C

of the n-ary relation m

i,n

When an n-ary relation m

i,n

satisﬁes these crite-

ria, m

i,n

is called a signature (Benayadi and Le Goc,

2008b). For Ta = 25% and Tc = 20%, all the n-ary

relations of the set M of the illustrative example are

signatures (S = M). These signatures are the only re-

lations (patterns) that are linked with the car system.

4 DISCUSSION

To evaluate the performance of TOM4L process, we

will report on the results obtained on the car exam-

ple (section 2) by TOM4L process and the three pop-

ular timed data mining algorithms Winepi(Mannila

et al., 1997), AprioriAll (Agrawal and Srikant, 1995)

and Minepi (Mannila et al., 1997). It shows that the

TOM4L process outperforms Winepi, AprioriAll and

Minepi in terms of the number of discovered patterns

and theirs accuracy. As we can see from the table

1 and the ﬁgure 3, TOM4L process outperforms the

three algorithms Winepi, AprioriAll and Minepi in

terms of number of the discovered patterns. Further-

more, TOM4L discovers patterns witch are consis-

tent with the structural model of the car system, while

most of the patterns discovered by Winepi, AprioriAll

and Minepi contradict this structural model.

Also, the three algorithms Winepi, AprioriAll and

Minepi require the setting of a set of parameters, so

the discovered patterns depend therefore on the val-

ues of this parameters (Mannila, 2002). To obtain an

interesting patterns, we must found the ideal set of pa-

rameters witch need to have some a priori knowledge

about the car system while this is precisely the global

aim of the Data Mining techniques.

Others experiments were made on sequences gen-

erated by complex dynamic process as blast furnace

process where they show that TOM4L approach con-

verges towards a minimal set of operational relations

and outperforms Winepi, AprioriAll and Minepi.

5 CONCLUSIONS

This paper presents the basis of the TOM4L process

for discovering temporal knowledge from timed mes-

sages generated by monitored dynamic process. The

TOM4L process is based on four steps: (1) a stochas-

tic representation of a given set of sequences from

which is induced (2) a minimal set of timed binary

relations, and an abductive reasoning (3) is then used

to build a minimal set of n-ary relations that is used to

ﬁnd (4) the most representativen-ary relations accord-

ing to the given set of sequences. The induction and

the abductive reasoning are based on an interesting-

ness measure of the timed binary relations that allows

eliminating the relations having no meaning accord-

ing to the given set of sequences. Our experiment

on a very simple illustrative process, the car system

shows that TOM4L process outperforms literature ap-

proaches.

REFERENCES

Agrawal, R. and Srikant, R. (1995). Mining sequential pat-

terns. Proceedings of the 11th International Confer-

ence on Data Engineering (ICDE95), pages 3–14.

Benayadi, N. and Le Goc, M. (2008a). Discovering tempo-

ral knowledge from a crisscross of observations timed.

The proceedings of the 18th European Conference on

Artiﬁcial Intelligence (ECAI’08). University of Patras,

Patras, Greece.

Benayadi, N. and Le Goc, M. (2008b). Using a measure of

the crisscross of series of timed observations to dis-

cover timed knowledge. In Proceedings of the 19th

International Workshop on Principles of Diagnosis

(DX’08), Blue Mountains, Australia.

Blachman, N. M. (1968). The amount of information that

y gives about x. IEEE Transcations on Information

Theory IT, 14.

Le Goc, M. (2006). Notion d’observation pour le diagnostic

des processus dynamiques: Application `a Sachem et `a

la d´ecouverte de connaissances temporelles. HDR,

Facult´e des Sciences et Techniques de Saint J´erˆome.

Mannila, H. (2002). Local and global methods in data min-

ing: Basic techniques and open problems. 29th In-

ternational Colloquium on Automata, Languages and

Programming.

Mannila, H., Toivonen, H., and Verkamo, A. I. (1997). Dis-

covery of frequent episodes in event sequences. Data

Mining and Knowledge Discovery, 1(3):259–289.

Shannon, C. E. (1949). Communication in the presence of

noise. Institute of Radio Engineers, 37.

MINING TIMED SEQUENCES TO FIND SIGNATURES

455