
CONSTRAINT REASONING IN FOCALTEST
Matthieu Carlier, Catherine Dubois
ENSIIE,
´
Evry, France
Arnaud Gotlieb
INRIA, Rennes, France
Keywords:
Software testing, Automated test data generation, MC/DC, Constraint reasoning.
Abstract:
Property-based testing implies selecting test data satisfying coverage criteria on user-specified properties.
However, current automatic test data generation techniques adopt direct generate-and-test approaches for
this task. In FocalTest, a testing tool designed to generate test data for programs and properties written in
the functional language Focal, test data are generated at random and rejected when they do not satisfy se-
lected coverage criteria. In this paper, we improve FocalTest with a test-and-generate approach, through the
usage of constraint reasoning. A particular difficulty is the generation of test data satisfying MC/DC on the
precondition of a property, when it contains function calls with pattern matching and higher-order functions.
Our experimental results show that a non-naive implementation of constraint reasoning on these constructions
outperform traditional generation techniques when used to find test data for testing properties.
1 INTRODUCTION
Property-based testing is a general testing technique
that uses property specifications to select test cases
and guide evaluation of test executions (Fink and
Bishop, 1997). It implies both selecting test inputs
from the property under test (PUT) and checking the
expected output results in order to evaluate the con-
formance of programs w.r.t. its property specifica-
tions. Applying property-based testing to functional
programing is not new. Claessen and Hugues pio-
nneered the testing of functional programs with the
Quickcheck tool (Claessen and Hughes, 2000) for
Haskell programs. Koopman et al. proposed a generic
automated test data generation approach called GAST
for functional programs (Koopman et al., 2002). The
tool GAST generates “common border values” and
random values from variable types. More recently,
Fisher et al. (Fischer and Kuchen, 2007; Fischer and
Kuchen, 2008) proposed an original data-flow cover-
age approach for the testing of Curry programs. This
approach is supported by the tool Easycheck (Chris-
tiansen and Fischer, 2008). In 2008, FocalTest (Car-
lier and Dubois, 2008), a tool that generates random
test data for Focalize programs was proposed. Focal-
ize (Dubois et al., 2006) is a functional language that
allows both programs and properties to be imple-
mented into the same environment. It also integrates
facilities to prove the conformance of programs to
user-specified properties. FocalTest is inspired by
Quickcheck as it implements a generate-and-test ap-
proach for test data generation: it automatically gen-
erates test inputs at random and reject those inputs
that do not satisfy the preconditions of properties
(Carlier and Dubois, 2008). This approach does not
perform well when strong preconditions are specified
and strong coverage criteria such as MC/DC are re-
quired on the preconditions. As a trivial example,
consider the generation of a couple (X,Y) where X
and Y stand for 32-bit integers, that has to satisfy the
precondition of property X = Y ⇒ f(X) = f(Y). For
a random test data generator, the probability of gener-
ating a couple that satisfies the precondition is
1
2
32
.
In this paper, we improve FocalTest with a test-
and-generate approach for test data selection through
the usage of constraint reasoning. The solution we
propose consists in exploring very carefully the pre-
condition part of the PUT and more precisely the def-
inition of the involved functions in order to produce
constraints upon the values of the variables. Then
it would remain to instantiate the constraints in or-
der to generate test cases ready to be submitted. The
82
Carlier M., Dubois C. and Gotlieb A. (2010).
CONSTRAINT REASONING IN FOCALTEST.
In Proceedings of the 5th International Conference on Software and Data Technologies, pages 82-91
DOI: 10.5220/0003009800820091
Copyright
c
SciTePress

underlying method to extract the constraints is based
on the translation of the precondition part of the PUT
and the body of the different functions involved in it
into an equivalent constraint logical program over fi-
nite domains - CLP(FD). Constraint solving relies on
domain filtering and constraint propagation, resulting,
if any, in solution schemes, that once instantiated will
give the expected test inputs.
The extraction of constraints and their resolution
have required to adapt the techniques developed in
(Gotlieb et al., 1998) to the specification and imple-
mentation language of Focalize, which is a functional
one, close to ML. In particular, an important technical
contribution of the paper concerns the introduction in
CLP(FD) of constraints related to values of concrete
types, i.e. types defined by constructors and pattern-
matching expressions, as well as constraints able to
handle higher-order function calls.
In this paper, we describe, here, the constraint rea-
soning part of FocalTest that permits to build a test
suite that covers the precondition with MC/DC (Mod-
ified Condition/Decision Coverage). This involves
the generation of positive test inputs (i.e. test inputs
that satisfy the precondition) as well as negative test
inputs. We evaluated our constraint-based approach
on several Focalize programs accompanied with their
properties. The experimental results show that a non-
naive implementation of constraint reasoning outper-
form traditional generation techniques when used to
find test inputs for testing properties.
The paper is organized as follows. Sec.2 pro-
poses a quick tour of the environment Focalize and
briefly summarises the background of our testing en-
vironment FocalTest which includes the subset of the
languageconsidered for writing programs and proper-
ties. Sec.3 details our translation scheme of a Focal-
ize program into a CLP(FD) constraint system. Sec.4
presents the test data generation by using constraints.
Sec.5 gives some indications about the implementa-
tion of our prototype and gives the results of an exper-
imental evaluation. Lastly we mention some related
work before concluding remarks and perspectives.
2 BACKGROUND
2.1 A Quick Tour of Focalize
Focalize is a functional language allowing the devel-
opment of programs step by step, from the specifica-
tion phase to the implementation phase. In our con-
text a specification is a set of algebraic properties de-
scribing relations over inputs and outputs of the Fo-
calize functions. The Focalize language is strongly
typed and offers mechanisms inspired by object-
oriented programming, e.g. inheritance and late bind-
ing. It also includes recursive (mutual) functions, lo-
cal binding (let x = e
1
in e
2
), conditionals (if e then
e
1
else e
2
), and pattern-matching expressions (match
x with pat
1
→ e
1
| ...| pat
n
→ e
n
). It allows higher-
order functions to be implemented but does not permit
higher-order properties to be specified for the sake of
simplicity. As an example, consider the Focalize pro-
gram and property of Figure1 where app (append)
and rev (reverse) both are user-defined functions. The
property called rev prop simply says that reversing a
list can be done by reversing its sub-lists.
let rec
app(L, G) =
match
L
with
|[] → G
|H :: T → H :: app(T, G);
let rec
rev aux(L, LL) =
match
L
with
|[] → LL
|H :: T → rev aux(T, H :: LL);
let
rev(L) = rev aux(L, []);
property
rev prop :
all
L L1 L2
:list(int),
L = app(L1, L2) → rev(L) = app(rev(L2), rev(L1));
Figure 1: A Focalize program.
In Focalize, variables can be of integer type (in-
cluding booleans) or of concrete type. Intuitively, a
concrete type is defined by a set of typed constructors
with fixed arity. Thus values for concrete type vari-
ables are closed terms, built from the type construc-
tors. For example, L in the rev prop of Focalize pro-
gram of Figure1 is of concrete type
list(int)
with
constructor [] of arity 0 and constructor :: of arity 2.
We do not detail further these features (details in
(Dubois et al., 2006)). We focus in the next section
on the process we defined to convert MC/DC require-
ments on complex properties into simpler requests.
2.2 Elementary Properties
A Focalize property is of the form P(X
1
, . . . , X
n
) ⇒
Q(X
1
, . . . , X
n
) where X
1
, . . . , X
n
are universally quan-
tified variables and P stands for a precondition while
Q stands for a post-condition. P and Q are both
quantifier free formulas made of atoms connected by
conjunction (∧), implication (⇒) and disjunction (∨)
operators. An atom is either a boolean variable B
i
,
the negation of a boolean variable ¬B
i
, a predicate
(e.g. X
i
= X
j
) holding on integer or concrete type
variables, a predicate involving function calls (e.g.
L = app(L1, L2)), or the negation of a predicate. Fo-
calize allows only first order properties, meaning that
properties can hold on higher order functions but calls
CONSTRAINT REASONING IN FOCALTEST
83

to these functions must instantiate their arguments
and universal quantification on functions is forbid-
den. Satisfying MC/DC on the preconditions of Fo-
calize properties requires building a test suite that
guarantees that the overall precondition being
true
and
false
at least once and, additionally requires
that each individual atom individually influences the
truth value of the precondition. The coverage crite-
rion MC/DC has been abundantly documented in the
literature, we do not detail it any further in this paper.
It is worth noticing that covering MC/DC on the pre-
conditions of general Focalize properties can be sim-
ply performed by decomposing these properties into a
set of elementary properties by using simple rewriting
rules. Assuming there is no coupling conditions (two
equivalent conditions), this rewriting system ensures
that covering MC/DC on the precondition of each de-
composed elementary property implies the coverage
of MC/DC on the original general property. More de-
tails on a preliminary version of this rewriting system
can be found in (Carlier and Dubois, 2008). An ele-
mentary property is of the form:
A
1
⇒ . . . ⇒ A
n
⇒ A
n+1
∨ . . . ∨ A
n+m
(1)
where the A
i
s simply denote atoms in the sense de-
fined below. For an elementary property P, the pre-
condition Pre(P) denotes A
1
∧ . . . ∧ A
n
while the con-
clusion Con(P) denotes A
n+1
∨ . . . ∨ A
n+m
. Property
rev prop of the Focalize program of Figure1 is an el-
ementary property of the form A
1
⇒ A
2
.
Covering MC/DC on the precondition Pre(P) of
an elementary property is trivial since Pre(P) is
made of implication operators only (⇒). Assuming
there are no coupling conditions in Pre(P), covering
MC/DC simply requires n + 1 test data: a single test
data where each atom evaluates to
true
and n test
data where a single atom evaluates to
false
while all
the others evaluate to
true
. In the former case, the
overall Pre(P) evaluates to
true
while in the latter it
evaluates to
false
. It is not difficult to see that such
a test suite actually covers MC/DC on Pre(P).
2.3 Test Verdict
A test data is a valuation which maps each integer or
concrete type variable X
i
to a single value. A posi-
tive test data for elementary property P is such that
Pre(P) evaluates to
true
while a negative test data is
such that Pre(P) evaluates to
false
. When test data
are selected, Con(P) can be used to assess a test ver-
dict which can be either OK, KO, or defined by the
user noted TBD (To Be Defined). The test verdict is
OK when a positive test data is selected and Con(P)
evaluates to
true
. The test verdict is KO when a
positive test data is selected and Con(P) evaluates to
false
. In this case, assuming that property P is cor-
rect, the selected test data exhibits a fault in the Focal-
ize PUT. Finally, the test verdict is TBD when a nega-
tive test data is selected. When the precondition of the
PUT evaluates to
false
, then the user has to decide
whether its Focalize program is correct or not in this
case. For example, if P is a safety property specify-
ing robustness conditions, then TBD should indeed be
KO. Conversely if P is a functional property specify-
ing an algebraic law (e.g. X + (Y +Z) = (X +Y)+Z),
then TBD should be inconclusive when negative test
data are selected.
In the paper, we only consider elementary proper-
ties (except in Sec.5.2) without coupling conditions
and focus on the problem of covering MC/DC on
these properties. Our test data generation method in-
volves the production of positive, as well as negative
test data. In both cases, each atom of the elemen-
tary property takes a predefined value (either
true
or
false
) and test data are required to satisfy constraints
on integer and concrete type variables. The rest of the
paper is dedicated to the constraint reasoning we im-
plemented to handle function calls that can be found
in atoms of precondition (such as L = app(L1, L2)).
Note that these function call involves constraints from
all the constructions that can be found in Focalize pro-
grams, including pattern-matching and higher-order
functions.
3 CONSTRAINT GENERATION
Each elementary property resulting from the rewriting
of PUT, more precisely its precondition, is translated
into a CLP(FD) program. When translating a precon-
dition, each Focalize function involved directly or in-
directly (via a call) in the precondition are also trans-
lated into an equivalent CLP(FD) program.
Our testing method is composed of two main
steps, namely constraint generation and constraint-
based test data generation. Figure2 summarizes our
overalltest data generationmethod with its main com-
ponents. A Focalize program accompanied with a
general property is first translated into an intermedi-
ate representation. The purpose of this transformation
is to remove all the oriented-object features of the Fo-
calize program by normalizing the code into an inter-
mediate language called MiniFocal. Normalization is
described in Sec.3.1. The second step involves the
construction of CLP(FD) programs, which are con-
straint programs that can be managed by a Constraint
Logic Programmingenvironment. As explained in the
previous section, the general property is dispatched
ICSOFT 2010 - 5th International Conference on Software and Data Technologies
84

into elementary properties and for each of them, a
single CLP(FD) program is generated. This process
is described in Sec.3.2. Finally, the FD solver coming
from our Constraint Logic Programming environment
is extended with specific constraint operators (namely
apply
and
match
) in order to solve requests, the solv-
ing of which guarantees the MC/DC coverage of each
individual elementary property. As a result, our test
data generation method produces a compliant MC/DC
test suite for the general property specified within the
Focalize PUT.
Focalize program + Property
MiniFocal program (intermediate representation)
CLP(FD) program
FD Solver +
apply
/
match
extension
MC/DC compliant test suite
Figure 2: Constraint solving procedure.
3.1 Normalization of Function
Definition
Each expression extracted from a function definition
is normalized into simpler intermediate expressions,
designed to ease the translation into a set of con-
straints. Figure3 gives the syntax of the intermediate
language MiniFocal.
expr ::= let x = expr in expr |
match x with
pat → expr; ... ; pat → expr;
[ → expr] |
op(x, ... , x) |
f(x, .. ., x) |
x(x, .. ., x) |
n | b | x | constructor(x, .. ., x)
pat ::= constructor | constructor(x, x)
Figure 3: Syntax of the MiniFocal language.
In MiniFocal, each expression used as an argu-
ment of a function call is assigned a fresh variable.
The same arises for decisions in conditional expres-
sions and pattern-matching operations. Furthermore,
patterns are linear (a variable occurs only once in
the pattern) and they cannot be nested. High-order
functions can be defined but the language cannot
cope with creation of closures and partial application.
Moreover, MiniFocal does not include if x then e
1
/else e
2
as this expression is translated into a match
expression match x with | true → e
2
| false → e
3
.
Such automatic normalization procedures are usual
in functional programming, Another less-usual nor-
malization procedure required by our method is the
so-called lambda-lifting transformation, described in
(Johnsson, 1985). It consists in eliminating free vari-
ables from function definitions. The purpose of these
transformations is to ease the production of CLP(FD)
programs.
3.2 Production of CLP(FD) Programs
The function definition (recursive or not) let [rec]
f(X
1
, . . . , X
n
) = E is translated into the CLP(FD) pro-
gram f(R, X
1
, . . . , X
n
) :- E. Thus a function is trans-
lated into a logical predicate with one clause that sets
the constraints derived from the body of the function.
R is a fresh output variable associated to the result of
f. E denotes the constraint resulting from the transla-
tion of E, according to the rules described below. In
the following we omit the overlines on objects in the
constraint universe when there is no ambiguity.
The translation of arithmetic and boolean expres-
sions is straightforward. A functional variable is
translated into a CLP(FD) variable. Next section ex-
plains what exactly a CLP(FD) variable is. The trans-
lation of the binding expression let X = E
1
in E
2
re-
quires first translating the output variable X and then
second translating expressions E1 and E2. For ex-
ample, let X = 5 ∗ Y in X + 3, is translated into the
constraint X = 5 ∗ Y ∧ R = X + 3, assuming the ex-
pression is itself bound to variable R. A function
call f(X
1
, . . . , X
n
), bound to variable R, is translated
into f(R, X
1
, . . . , X
n
). In the case of recursive func-
tion, this is the natural recursion of Prolog that han-
dles recursion of MiniFocal functions. A higher-order
function call X(X
1
, . . . , X
n
) where X denotes any un-
known function is translated into the specific con-
straint combinator
apply
with the following pattern
apply
(X, [X
1
, . . . , X
n
]). The constraint
apply
is de-
tailed in Sec.4. Similarity, the pattern-matching ex-
pression is translated into a constraint combinator
match
. This constraint takes the matched variable as
first argument, the list of pattern clauses with their
body as second argument, and the default case pat-
tern as third argument (
fail
when there is no default
case). As an example, consider a pattern-matching
expression of Figure1:
match L with [] → G; H :: T → H :: app(T, G);
is translated into
match
(L, [ pattern([], R = G),
pattern(H :: T, app(R1, T, G), R = H :: R1)],
fail
).
CONSTRAINT REASONING IN FOCALTEST
85

4 CONSTRAINT-BASED TEST
DATA GENERATION
Constraint-based test data generation involves solv-
ing constraint systems extracted from programs. In
this section, we explain the key-point of our ap-
proach consisting in the implementation of the con-
straint combinators we introduced to model faithfully
higher-order function call and pattern-matching ex-
pressions. First we briefly recall how CLP(FD) pro-
gram are handled by a Prolog interpreter (Sec.4.1),
second we explain our new dedicated constraint com-
binators (Sec.4.2), third we present the test data label-
ing process (Sec.4.3) and finally we discuss the cor-
rection of our constraint model (Sec.4.4).
4.1 Constraint Solving
A CLP(FD) program is composed of variables, built-
in constraints and user-defined constraints. There are
two kinds of variables: free variables that can be uni-
fied to Prolog terms and FD variables for which a
finite domain is associated. The constraint solving
process aims at pruning the domain of FD variables
and instantiating free variables to terms. Built-in con-
straints such as +, −, ∗, min, max . . ., are directly en-
coded within the constraint library while user-defined
constraints can be added by the user either under the
form of new Prolog predicate or new constraint com-
binators. Unification is the main constraint over Pro-
log terms. For example, t(r(1, X), Z) = t(H, r(2)) re-
sults in solutions H = r(1, X) and Z = r(2).
Intuitively, a CLP(FD) program is solved by
the interleaving of two processes, namely constraint
propagation and labeling. Roughly speaking, con-
straint propagation allows reductions to be propa-
gated throughout the constraint system. Each con-
straint is examined in turn until a fixpoint is reached.
This fixpoint corresponds to a state where no more
pruning can be performed. The labeling process tries
to instantiate each variable X to a single value v of its
domain by adding a new constraint X = v to the con-
straint system. Once such a constraint is added, con-
straint propagation is launched and can refine the do-
main of other variables. When a variable domain be-
comes empty, the constraint system is showed incon-
sistent (that is the constraint system has no solution),
then the labeling process backtracks and other con-
straints that bind values to variables are added. To ex-
emplify those processes, consider the following (non-
linear) example: X,Y in 0..10∧X ∗Y = 6∧X +Y = 5.
First the domain of X and Y is set to the interval 0..10,
then constraint X ∗Y = 6 reduces the domain of X and
Y to 1..6 as values {0, 7, 8, 9, 10} cannot be part of so-
lutions. Ideally, the process could also remove other
values but recall that only the bounds of the domains
are checked for consistency and 1∗6 = 6∗ 1 = 6. This
pruning wakes up the constraint X + Y = 5, that re-
duces the domain of both variables to 1..4 because
values 5 and 6 cannot validate the constraint. Finally
a second wake-up of X ∗ Y = 6 reduces the domains
to 2..3 which is the fixpoint. The labeling process
is triggered and the two solutions X = 2,Y = 3 and
X = 3,Y = 2 are found.
4.2 Dedicated Constraint Combinators
In CLP(FD) programming environments, the user can
define new constraint combinators with the help of
dedicated interfaces. Defining new constraints re-
quires to instantiate the following three points:
1. A constraint interface including a name and a set
of variables on which the constraint holds. This is
the entry point of the newly introduced constraint;
2. The wake-up conditions. A constraint can be
awakened when either the domain of one of its
variables has been pruned, or one of its variables
has been instantiated, or a new constraint related
to its variables has been added;
3. An algorithm to call on wake-up. The purpose
of this algorithm is to check whether or not the
constraint is consistent
1
with the new domains of
variables and also to prune the domains.
The CLP(FD) program generated by the transla-
tion of MiniFocal expressions (explained in Sec.3) in-
volves equality and inequality constraints over vari-
ables of concrete types, numerical constraints over
FD variables, user-defined constraints used to model
(possibly higher-order) function calls and constraint
combinators
apply
and
match
.
The domain of FD variables is generated from
MiniFocal variables using their types. For example,
MiniFocal 32-bits integer variable are translated into
FD variables with domain 0..2
32
− 1. Variables with
a concrete type are translated into fresh Prolog vari-
ables that can be unified with terms defined upon
the constructors of the type. For example, the vari-
able L of concrete type list(int) has infinite domain
{[], 0 :: [], 1 :: [], . . . , 0 :: 0 :: [], 0 :: 1 :: [], . . .}.
4.2.1 apply Constraint
The constraint combinator
apply
has interface
apply
(F, L) where F denotes a (possibly free) Prolog
variable and L denotes a list of arguments. Its wake-
up condition is based on the instantiation of F to the
1
If there is a solution of the constraint system.
ICSOFT 2010 - 5th International Conference on Software and Data Technologies
86

name of a function in the MiniFocal program. The en-
coding of
apply
follows the simple principle of sus-
pension. In fact, any
apply
(F, L) constraint suspends
its computation until the free variable F becomes in-
stantiated. Whenever F is bound to a function name,
then the corresponding function call is automatically
built using a specific Prolog predicate called =... This
higher-order predicate is able to build Prolog terms
dynamically. To make things more concrete, consider
the following simplified implementation of
apply
:
apply
(F, L)
:- freeze
(F,CALL =.. F::L, CALL)
If L represents a list of arguments X
1
:: X
2
:: [], this
code just says that when F will be instantiated to a
function name f, the term f(X
1
, X
2
) will be created
and called. This is a simple but elegant way of dealing
with higher-order functions in CLP(FD) programs.
4.2.2 match Operator
The
match
constraint combinator has interface
match
(X, [pattern(pat
1
, C
1
), .. ., pattern(pat
n
, C
n
)],
C
d
) where C
1
, . . . ,C
n
,C
d
denote FD or Prolog con-
straints. The wake-up conditions of the combinator
include the instantiation of X or just the pruning of the
domain of X in case of FD variable, the instantiation
or pruning of variables that appear in C
1
, . . . ,C
n
,C
d
.
The algorithm launched each time the combinator
wakes up is based on the following rules:
1. if n = 0 then
match
rewrites to default case C
d
;
2. if n = 1, and C
d
=
fail
, then
match
rewrites to
X = pat
1
∧ C
1
;
3. if ∃i in 1..n such that X = pat
i
is entailed by the
constraint system, then
match
rewrites to C
i
;
4. if ∃i in 1..n such that ¬(X = pat
i
∧ C
i
) is
entailed by the constraint system then
match
rewrites to
match
(X, [pattern(pat
1
,C
1
), ...,
pattern(pat
i−1
,C
i−1
), pattern(pat
i+1
,C
i+1
), . ..,
pattern(pat
n
,C
n
, C
d
)], C
d
).
The two former rules implement trivial terminal
cases. The third rule implements forward deduction
w.r.t. the constraint system while the fourth rule im-
plements backward reasoning. Note that these two
latter rules use nondeterministic choices to select the
pattern to explore first. To illustrate this combinator,
consider the following example:
match
(L, [ pattern(
[]
, R = 0), pattern(H :: T, R =
H + 10)],
fail
) where R is FD variable with domain
6..14 and L is of concrete type list(int). As con-
straint ¬(L =
[]
∧ R = 0) is entailed by current do-
mains when the fourth rule is examined (R = 0 and
R ∈ 6..14 are incompatible), the constraint rewrites to
match
(L, [ pattern(H :: T, R = H + 10)],
fail
)
and the second rule applies as it remains only a single
pattern: L = H :: T ∧R = H + 10. Finally, pruning the
domains leads to R ∈ 6..14, H ∈ −4..4, and L = H :: T
where T stands for any list(int) variable.
4.3 Test Data Labeling
As mentioned below, constraint solving involves vari-
able and value labeling. In our framework, we give
labels to variables of two kinds: FD variables and
Prolog variables representing concrete types coming
from MiniFocal programs. As these latter variables
are structured and involve other variables (such as in
the above example of list(int)), we prefer to instanti-
ate them first. Note that labeling a variable can awake
other constraints that hold on this variable and if a
contradiction is found, then the labeling process back-
tracks to another value or variable. Labeling FD vari-
ables requires to define variable and value to enumer-
ate first. Several heuristics exist such as labeling first
the variable with the smallest domain (first-fail prin-
ciple) or the variable on which the most constraints
hold. However, in our framework, we implemented an
heuristic known as random iterative domain-splitting.
Each time a non-instantiated FD variable X is se-
lected, this heuristic picks up at random a value v into
the current bound of the variable domain, and add the
following Prolog choice points (X = v;X < v;X > v).
When the first constraint X = v is refuted, the pro-
cess backtracks to X < v and selects the next non-
instantiated variable while adding X to the queue of
free variables. This heuristic usually permits to cut
down large portions of the search space very rapidly.
It is worth noticing that once all the variables have
been instantiated and the constraints verified then we
hold a test input that satisfies the elementary PUT.
4.4 Correctness, Completeness and
Non-termination
Total correctness of our constraint model implies
showing correctness, completeness and termination.
If we make the strong hypothesis that CLP(FD) pred-
icates correctly implement arithmetical MiniFocal op-
erators and that the underlying constraint solver is
correct, then the correctness of our model is guaran-
teed, as the deduction rules of
match
directly follow
from the operational semantics of conditional and pat-
tern matching in Focalize. Completeness comes from
the completeness of the labeling process in CLP(FD).
In fact, as soon as every possible test data is possi-
bly enumerated during the labeling step, any solution
will be eventually found. But completeness comes
at the price of efficiency and preserving it may not
be indispensable in our context. A proof of the cor-
CONSTRAINT REASONING IN FOCALTEST
87

rectness and the completeness has been written (Car-
lier, 2009). It required to specify the formal semantics
of the Focalize functional language, the semantics of
constraints, to define formally the translation and the
notion of solution of a constraint system derived from
a Focalize expression. We have formally proved that
if we obtain a solution of the CLP(FD) program, i.e.
an assignment of variables of this program, then the
evaluation of the precondition, according to the Focal-
ize operational semantics yields the expected value.
Our approach has no termination guarantee as
we cannot guarantee the termination of any recursive
function and guarantee the termination of the label-
ing process. Hence, it is only a semi-correct proce-
dure. To leverage the problems of non-termination,
we introduced several mechanisms such as time-out,
memory-out and various bounds on the solving pro-
cess. When such a bound is reached, other label-
ing heuristics are tried in order to avoid the problem.
Note however that enforcing termination yields losing
completeness as this relates to the halting problem.
5 IMPLEMENTATION AND
RESULTS
5.1 Implementation
We implemented our approach in the FocalTest tool
(Carlier and Dubois, 2008). It takes a Focalize pro-
gram and a (non-elementary) property P as input and
produces a test set that covers MC/DC on the pre-
condition of P as output. The tool includes a parser
for Focalize, a module that breaks general proper-
ties into elementary ones, a preprocessor that normal-
izes function definitions and the elementary proper-
ties, a constraint generator, a constraint library that
implements our combinators and a test harness gener-
ator. FocalTest is mainly developed in SICStus Pro-
log and makes an extensive use of the CLP(FD) li-
brary of SICStus Prolog. This library implements sev-
eral arithmetical constraints as well as labeling heuris-
tics. The combinator
match
is implemented using the
SICStus global constraint interface; It is considered
exactly as any other FD constraint of the CLP(FD)
library. Our experiments have been computed on a
3.06Ghz clocked Intel Core 2 Duo with 4Gb 1067
MHz DDR3 SDRAM. Integer are encoded on 16 bits.
5.2 Experimental Evaluation
Firstly, we wanted to evaluate if constraint reasoning
brought something to the test data generation process
in FocalTest. Second, we wanted to evaluate sev-
eral possible implementations of our constraint com-
binators. In particular, we wanted to evaluate a “full
constraint reasoning” approach against two naive ap-
proaches: using Prolog choice points to explore the
branches of
match
constraints, using only forward
constraint reasoning rules (e.g. only rules 1-2-3 of the
implementation of
match
). This last experience was
designed to evaluate the advantage of using backward
reasoning rule (e.g. rule 4 of
match
). For the eval-
uation of “constraint reasoning” w.r.t. a random test
data generation approach, we compared FocalTestnot
only with the previous implementation (Carlier and
Dubois, 2008), but also with QuickCheck (Claessen
and Hughes, 2000) the mainstream tool for test data
generation of Haskell programs.
Context of the Experiment. We evaluated Focal-
Test as follows on 6 examples (listed below) and
asked FocalTest to generate 10 MC/DC-compliant
test suite for each property. For all examples and
strategies, we measured CPU runtime with the Unix
time command and computed the average time. The
time required to generate the CLP(FD) program, to
produce test harness, to execute Focalize program
with the generated test data have not been computed
in order to fairly evaluate our distinct versions. We
also dropped trivial test data only based on empty lists
or singletons, which are of limited interest for a tester.
Focalize Programs.
Avl
is an implementation of
AVL trees. The PUT says that inserting an element
into an AVL (of integers) still results in an AVL:
is avl
(t) →
is avl
(
insert avl
(e,t))
Three properties hold on lists:
sorted list
(2) is
similar to
insert avl
but holds over sorted lists;
min max
(3) is a simple property on integer optima
from lists; and
sum list
(4) speaks of the sum of in-
teger elements of a list.
∀t ∈
list(int)
, ∀e ∈
int
,
sorted
(t) →
sorted
(
insert list(e,t)
)
(2)
∀l ∈
list(int)
, ∀min, max, e ∈
int
,
is min
(min, l) →
is max
(max, l) →
(
min list
(e :: l) =
min int
(min, e) ∧
max list
(e :: l) =
max int
(max, e))
(3)
s1 =
sum list
(l1) → s2 =
sum list
(l2) →
s1+ s2 =
sum list
(
append
(l1, l2))
(4)
The
triangle
function takes three lengths as in-
puts and returns a value saying whether if the
corresponding triangle is
equilateral
,
isocele
,
ICSOFT 2010 - 5th International Conference on Software and Data Technologies
88

Table 1: Random/Constraint test data generation time comparison (in milliseconds).
Programs Properties QuickCheck Random FocalTest constraint reasoning Speedup
time nb generated FocalTest factor
avl
See Sec.5.2 48,007 10,288,259 22,531,719 10,061 5.8
sorted list
See Sec.5.2 515 2 1,090 54 9.5
min max
See Sec.5.2
Fail
147,202 20,007,999 264 557.6
sum list
See Sec.5.2
Fail
133,139 13,444,919 55 2,420.7
Triangle
equilateral
Fail
70,416 12,710,142 113 623.2
Voter
range c1 2,863 708 136,537 87 32.9
range c2 3,556 742 142,387 80 44.5
partial c1
Fail Fail
- 486 +∞
partial c2
Fail Fail
- 430 +∞
scalene
or
invalid
. For example, property
tri correct equi
:
triangle
(x, y, z) =
equilateral
→ x = y ∧ y = z
Voter
is a component used in the industry for
computing a unique value from data obtained via
three sensors (Ayrault et al., 2008). The func-
tion
vote
takes three integers as inputs and re-
turns a pair composed of an integer and a value in
{
Match
,
Nomatch
,
Perfect
}.
Perfect
means that
the difference between two inputs is less than 2
while other tags describe similar properties. Property
vote perfect
) says:
compatible
(v1, v2) →
compatible
(v2, v3) →
compatible
(v1, v3) →
compatible
(
fst
(
vote
(v1, v2, v3)), v1) ∧
snd
(
vote
(v1, v2, v3)) =
Perfect
These properties contain recursive functions with
heavy use of pattern matching and combination of
structures of concrete types (lists and trees over nu-
merical values), as well as conditionals.
The last property executed aims at evaluating con-
straint reasoning in presence of higher order fea-
tures. The property is : l
2
=
map
(
successor
, l
1
) →
sigma
(l
2
) =
map
(
successor
,
sigma
(l
1
)). The sec-
ond order function
map
takes f and a list l as inputs
and returns a list obtained by applying f on each el-
ement of l.
sigma
implements a permutation. Our
results show that FocalTest can generate 10 test cases
(where (l1, l2) is made of two 1,000-elements lists) in
less than five seconds.
5.3 Results
Tab. 1 shows the results obtained with the ran-
dom based approach, more precisely the first column
presents the time required for QuickCheck to generate
the test suite. The two next columns represent random
in FocalTest(CPU time and number of test data gener-
ated until we obtain 10 adequate test data). The fourth
column contains the CPU time required for FocalTest
with constraint reasoning to generate the test cases.
The last column highlights the gain factor between
QuickCheck (or random FocalTest when QuickCheck
fails) and FocalTest with constraint reasoning.
Firstly, note that two properties of
triangle
are
easily covered with both random test data genera-
tors. This is not astonishing since these properties
require the three lengths to form a scalene triangle or
an invalid triangle. The
sorted list
example is also
tractable with the random approaches as small lists
are generated (4 elements) and the probability to gen-
erate sorted lists in this case is high. In general, the
results of QuickCheck fits the results obtained with
the random test data generator of FocalTest (without
constraint reasoning) but QuickCheck is usually more
efficient. Secondly, note that for most of the other
examples, both random approaches fail to find any
test data (failure is reported when more than 10 mil-
lions of consecutive non-adequate test data are gen-
erated). Nevertheless, FocalTest with constraint rea-
soning finds MC/DC-compliant test suites with an av-
erage speed up factor of 23 w.r.t. QuickCheck (when
QuickCheck does not fail).
Thirdly, Tab.2 compares the CPU time required by
three distinct implementations of the
match
operator.
full
denotes “full constraint reasoning” such as de-
scribed in the paper,
noback
denotes an implemen-
tation without backward reasoning rules, and
choice
denotes an implementation with Prolog choice points.
Thus,
match
(x, [pattern(pat
1
, C
1
), .. ., pattern(pat
n
,
C
n
)], C
d
) is implemented with (x = pat
1
,C
1
);. . . ;(x =
pat
n
,C
n
);(x 6= pat
1
, . . . , x 6= pat
n
,C
d
).
For some examples,
choice
and
full
give simi-
lar results which was unexpected (triangle and some
properties of Voter). In fact, these examples con-
tain few execution paths and our
choice
implemen-
tation of
match
makes the corresponding CLP(FD)
programs having few choice points. Thus, these ex-
amples are less sensitive to constraint reasoning. On
the contrary, for all other examples, we got a speedup
factor in between 3.7 and 2789. This is not surprising
as constraint reasoning can capture disjunctive infor-
mation while choice points cannot.
For the triangle example,
noback
fails because
CONSTRAINT REASONING IN FOCALTEST
89

constraint inconsistency is detected only when all
the variables are instantiated. In some examples,
backward reasoning is not used for improving the
time required to generate test data (
sorted list
and
Voter
). However, on these examples, one can see that
backward reasoning does not slow down the process.
On other example, backward reasoning is useful and
improve the CPU time required to generate test data.
In conclusion, these experiments show firstly, that
constraints helps to find test data for testing proper-
ties, especially when random generation fails. Sec-
ondly, the choice of using operators like
match
to-
gether with forward and backward reasoning rules
speeds up the computation of a solution. An Pro-
log choice points implementation is ineffective when
there are numerous execution paths in a program.
6 RELATED WORK
Using constraint solving techniques to generate test
cases is not a new idea. (Dick and Faivre, 1993) and
(Marre, 1991) were among the first to introduce Con-
straint Logic Programming for generating test cases
from specification models such as VDM or algebraic
specifications. These seminal works yield the devel-
opment of GATEL, a tool that generates test cases for
reactive programs written in Lustre. In 1998, Gotlieb
et al. proposed using constraint techniques to gen-
erate test data for C programs (Gotlieb et al., 1998).
This approach was implemented in tools InKa and
Euclide (Gotlieb, 2009). In (Legeard and Peureux,
2001) set solving techniques were proposed to gen-
erate test cases from B models. These ideas were
pushed further through the development of the BZ-
TT and JML-TT toolset. In 2001, Pretschner devel-
oped the model-based test case generator AUTOFO-
CUS that exploited search strategies within constraint
logic programming (Pretschner, 2001) and recently,
PathCrawler introduced dynamic path-oriented test
data generation (Williams et al., 2005). This method
was independently discovered in the DART/CUTE
approach (Godefroid et al., 2005; Sen et al., 2005).
In the case of testing functional programs,
most approaches derive from the QuickCheck tool
(Claessen and Hughes, 2000) which generates test
data at random. GAST is a similar implementation
for Clean, while EasyCheck implements random test
data generation for Curry (Christiansen and Fischer,
2008). QuickCheck and GAST implement function
generators for higher-order function since they deal
with higher-order properties while this is not neces-
sary in our approach because such properties are not
allowed in Focalize. Easycheck resembles to FocaTe-
st because it takes advantage of the original language
features such as free variable and narrowing to gen-
erate automatically test cases w.r.t. a property. These
features could be related to clause definition, back-
tracking and labeling in CLP(FD) program without
constraint aspects. FocalTest originally takes inspira-
tions from these tools, that is, to test a functional pro-
gram against a property. As far as we know, FocalTest
is the first application of constraint solving in the area
of test data generation for functional programs.
The development of SAT-based constraint solver
for generating test data from declarative models also
yields the development of Kato (Uzuncaova and
Khurshid, 2008) that optimizes constraint solving
with (Alloy) model slicing. Like some of the above
tools such as GATEL, AUTOFOCUS or EUCLIDE,
FocalTest relies on finite domains constraint solving
techniques. But, it has two main differences with
these approaches. Firstly, it is integrated within a
environment which contains naturally property that
could be used for testing. Secondly, it uses its ownop-
erators implementation for generating test data in the
presence of conditionals and pattern-matching opera-
tions and concrete type. This allows various deduc-
tion rules to be exploited to find test data that satisfy
properties. Unlike traditional generate-and-test ap-
proaches, this allows one to exploit constraints to in-
fer new domain reductions and then helps the process
to converge more quickly towards sought solutions.
7 CONCLUSIONS
The constraint-based approach we proposed is a gen-
eral one that allows us to obtain an MC/DC compli-
ant test suite that satisfies the precondition part of Fo-
calize properties. This approach is based on a sys-
tematic translation of Focalize program into CLP(FD)
programs and relies on the definition of efficient con-
straint combinators to tackle pattern-matching and
higher-order functions. We integrated this constraint-
reasoning to FocalTest and relieves it from using in-
efficient generate-and-test approaches to select test
data satisfying given preconditions. Our experimen-
tal evaluation shows that using constraint reasoning
for this task outperforms traditional random test data
generation by a factor of 23.
Furthermore this work can be reused for test gen-
eration in other functional languages, for example to
extend test selection in QuickCheck-like tools (that
rely on random or user-guided generation). Further-
more exploring how the constraint model of the over-
all properties and programs could be used to formally
prove the conformance of the program to its specifica-
ICSOFT 2010 - 5th International Conference on Software and Data Technologies
90
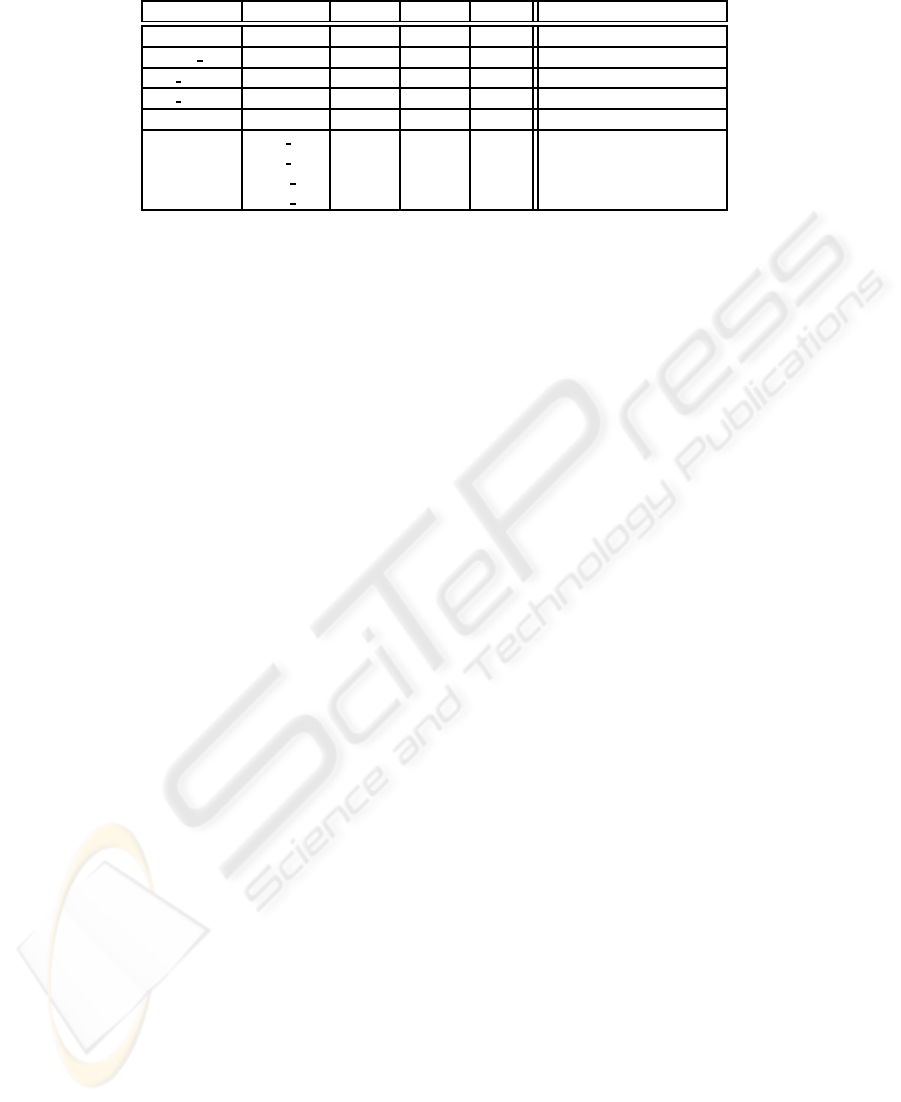
Table 2: CPU time required by distinct implementations of match in FocalTest (in milliseconds).
Programs Properties noback choice full Speedup factor (choice/full)
avl
See Sec.5.2 149,131 37,302 10,061 3.7
sorted list
See Sec.5.2 68 150,612 54 2,789.1
min max
See Sec.5.2 1,466 120,318 264 455.8
sum list
See Sec.5.2 137 38,924 55 707.7
Triangle
equi
Fail
112 113 1.0
Voter
range c1 40 23 87 0.3
range c2 36 986 80 12.3
partial c1 103 2,590 486 5.3
partial c2 304 22 430 0.5
tions needs further investigation. Exploiting con-
straint solving in software verification is likely to be
an important topic able to enlight the convergence of
proofs and tests.
REFERENCES
Ayrault, P., Hardin, T., and Pessaux, F. (2008). Develop-
ment life cycle of critical software under focal. In Int.
Workshop on Harnessing Theories for Tool Support in
Software, TTSS.
Carlier, M. (2009). Constraint Reasoning in Focal-
Test. CEDRIC Technical report, available on
http://cedric.cnam.fr.
Carlier, M. and Dubois, C. (2008). Functional testing in the
focal environment. In Test And Proof, TAP.
Christiansen, J. and Fischer, S. (2008). Easycheck – test
data for free. In 9th Int. Symp. on Func. and Logic
Prog, FLOPS.
Claessen, K. and Hughes, J. (2000). QuickCheck: a
lightweight tool for random testing of Haskell pro-
grams. ACM SIGPLAN Notices, 35(9):268–279.
Dick, J. and Faivre, A. (1993). Automating the generation
and sequencing of test cases from model-based spec-
ifications. In First Int. Symp. of Formal Methods Eu-
rope, FME, pages 268–284.
Dubois, C., Hardin, T., and Vigui´e Donzeau-Gouge, V.
(2006). Building certified components within focal.
In Fifth Symp. on Trends in Functional Prog., TFP’04,
volume 5, pages 33–48.
Fink, G. and Bishop, M. (1997). Property-based testing:
a new approach to testing for assurance. SIGSOFT
Softw. Eng. Notes, 22(4):74–80.
Fischer, S. and Kuchen, H. (2007). Systematic generation
of glass-box test cases for functional logic programs.
In Conf. on Princ. and Practice of Declarative Pro-
gramming (PPDP’07), pages 63–74.
Fischer, S. and Kuchen, H. (2008). Data-flow testing of
declarative programs. In Proc. of ICFP’08), pages
201–212.
Godefroid, P., Klarlund, N., and Sen, K. (2005). Dart: di-
rected automated random testing. In ACM Conf. on
Prog. lang. design and impl., PLDI, pages 213–223.
Gotlieb, A. (2009). Euclide: A constraint-based testing
platform for critical c programs. In Int. Conf. on Soft-
ware Testing, Validation and Verification, ICST.
Gotlieb, A., Botella, B., and Rueher, M. (1998). Au-
tomatic test data generation using constraint solving
techniques. In Int. Symp. on Soft. Testing and Analy-
sis, ISSTA, pages 53–62.
Johnsson, T. (1985). Lambda lifting: Transforming pro-
grams to recursive equations. In Conference on Func-
tional Programming Languages and Computer Archi-
tecture, pages 190–203. Springer-Verlag.
Koopman, P., Alimarine, A., Tretmans, J., and Plasmeijer,
R. (2002). Gast: Generic automated software testing.
In Workshop on the Impl. of Func. Lang., IFL02, pages
84–100. Springer.
Legeard, B. and Peureux, F. (2001). Generation of func-
tional test sequences from B formal specifications -
presentation and industrial case-study. In Int. Conf.
on Automated Soft. Eng., ASE01, pages 377–381.
Marre, B. (1991). Toward Automatic Test Data Set Se-
lection using Algebraic Specifications and Logic Pro-
gramming. In K. Furukawa, editor, Int. Conf. on Logic
Programming, ICLP, pages 202–219.
Pretschner, A. (2001). Classical search strategies for test
case generation with constraint logic programming. In
Formal Approaches to Testing of Soft., FATES, pages
47–60.
Sen, K., Marinov, D., and Agha, G.(2005). Cute: a concolic
unit testing engine for c. In ESEC/FSE-13, pages 263–
272. ACM Press.
Uzuncaova, E. and Khurshid, S. (2008). Constraint prioriti-
zation for efficient analysis of declarative models. In
15th Int. Symp. on Formal Methods, FM.
Williams, N., Marre, B., Mouy, P., and Roger, M. (2005).
Pathcrawler: Automatic generation of path tests by
combining static and dynamic analysis. In Depend-
able Computing, EDCC, pages 281–292.
CONSTRAINT REASONING IN FOCALTEST
91
