
MUTATION TESTING STRATEGIES
A Collateral Approach
Mike Papadakis, Nicos Malevris and Marinos Kintis
Department of Informatics Athens University of Economics and Business, Patission Street 76, 10434, Athens, Greece
Keywords: Mutation testing, Weak mutation, Higher order mutation, Collateral coverage.
Abstract: Mutation Testing is considered to be one of the most powerful techniques for unit testing and at the same
time one of the most expensive. The principal expense of mutation is the vast number of imposed test
requirements, many of which cannot be satisfied. In order to overcome these limitations, researchers have
proposed many cost reduction techniques, such as selective mutation, weak mutation and a novel approach
based on mutant combination, which combines first order mutants to generate second order ones. An
experimental comparison involving weak mutation, strong mutation and various proposed strategies was
conducted. The experiment shows that all proposed approaches are quite effective in general as they result
in high collateral coverage of strong mutation (approximately 95%), while recording remarkable effort
savings. Additionally, the results suggest that some of the proposed approaches are more effective than
others making it possible to reduce the mutation testing application cost with only a limited impact on its
effectiveness.
1 INTRODUCTION
The software testing activity forms one of the most
widely used methods for both revealing software
faults and establishing confidence about the normal
behaviour of the software products. This activity
requires the generation and execution of the software
under test with actual test data. Their quality is
measured by their ability to exercise certain program
features. Based on the necessity and importance of
exercising specific program features various test
adequacy measures have been proposed. Measures
of this kind give rise to the definition of various
testing criteria usually referred to as coverage
criteria. Given one such criterion say branch
coverage the tester is required to produce test cases
until they satisfy-cover all the test elements defined
by the criterion i.e. all program branches.
Mutation testing is a fault based technique used
for producing high quality test cases. It injects
specific faults into the software under test and
requires from the tester to produce test cases able to
reveal them. By requiring the production of mutation
adequate test cases it is believed that a high level of
testing thoroughness can be achieved. This is
supported by the recent experiments of (Andrews et
al., 2006) which provide evidence that the mutation
technique can produce faults similar to real ones and
can thus provide a good estimate of the fault
revealing ability of the candidate test case sets.
Despite its effectiveness, mutation often requires
unacceptable (unlimited) computational resources.
This is a direct consequence of the vast number of
faulty program versions that it introduces. To bypass
these shortcomings researchers have proposed a
number of techniques aiming at reducing the cost
involved (Offutt and Untch, 2001) while keeping its
effectiveness at a high level. Recently, a new
mutation testing alternative approach has been
suggested, based on the notion of higher order
mutants (Polo et al., 2009), which consists of
combining pairs of first-order mutants to obtain a set
of second-order ones.
In this study various second order mutation
testing strategies are proposed and their behaviour in
providing collateral coverage (Malevris and Yates,
2006) with respect to strong mutation is
investigated. Additionally a comparison with
another mutation alternative technique namely weak
mutation was also undertaken. The results indicate
that second order mutation testing strategies form a
viable alternative of mutation as they can achieve
considerable effort savings, without significant loss
of test effectiveness.
325
Papadakis M., Malevris N. and Kintis M. (2010).
MUTATION TESTING STRATEGIES - A Collateral Approach.
In Proceedings of the 5th International Conference on Software and Data Technologies, pages 325-328
DOI: 10.5220/0003012903250328
Copyright
c
SciTePress

2 BACKGROUND
Mutation testing is a well known fault-based
technique which was established and introduced by
(Hamlet, 1977) and (DeMillo et al., 1978). Mutation
induces syntactic faults into the software’s under test
code by creating many versions of the original
program (mutants). Test cases are used to execute
the generated mutants with the goal of distinguishing
(killing) them from the original one, by causing them
to result in incorrect output. A mutant is called
equivalent if the inexistence of such test cases holds.
Measuring the testing quality based on the ratio of
killed mutants results in a mutation based metric.
This metric is usually called mutation score and it is
defined as the ratio of killed mutants over the total
number of non-equivalent mutants.
Various approaches have been proposed in order
to make mutation testing more practical. Weak
mutation (Howden, 1982) reduces the computational
expense of mutation by avoiding the complete
execution of the generated mutants. It suggests
stopping the program execution immediately after
the execution of the mutated statements. Based on
this, execution savings rely on the reduced execution
traces. In the present study it was decided to use
weak mutation for comparison between the methods,
since it has proved to be more cost-effective than
strong mutation e.g. (Offutt and Lee, 1994).
Recently a new mutation testing alternative
approach has been proposed (Polo et al., 2009),
based on the notion of second order mutants.
According to this, based on a set of candidate
mutants, a reduced set of second order mutants is
formed by combining them into pairs. Various
strategies of how and which mutant statements
should be combined can be conducted. In the study
of (Polo et al., 2009) three strategies were proposed
and their experimental results showed high reduction
on the number of generated and equivalent mutants.
Additionally, evidence about the cost-effectiveness
of the use of second order strategies was provided by
(Papadakis and Malevris, 2010). It is this conclusion
that is investigated in the present study by using
partly some of the originally proposed and partly
some newly proposed strategies. This is done in
order to determine the impact on the testing quality
of the second order mutation strategies in
comparison to that of strong and weak mutation.
3 SECOND ORDER MUTATION
Besides the investigation of the cost and benefits of
using second order mutation an additional goal was
to propose new strategies able to provide better
results than the initially ones. To achieve this, a set
of six new strategies was developed. Due to lack of
space only a brief description of these strategies is
given. Their full details can be found in (Kintis, 2010).
The proposed strategies fall into three general
categories: a) The Dominator category denoted as
Dom, b) the Relaxed Dominator denoted as RDom
and c) the Strict Dominator denoted as SDom. These
three categories are based on the dominator analysis
(Agrawal, 1994) of the programs under test. The
idea behind their use was to increase the coupling
chances between the introduced mutants. To achieve
this, the mutant pairs were forced to be selected
from node pairs that were found to have a
domination relation.
The Dominator strategy category starts by
constructing the sets of pre and post dominating
nodes say pre-n and post-n for each node, say n, of
the program’s control flow graph. Then it selects
mutants from node n and combines them with those
from pre-n and post-n nodes by selecting at least one
mutant from either of the two. It must be noted that
this category guarantees the equal contribution of the
pre and post dominating nodes at the second order
mutant generation process. Figure 1 illustrates the
sequence of node pairs, generated for node 4, from
which the second order mutants will be created. The
sequence shown will be repeated until all mutants of
node 4 are combined.
Figure 1: The sequence of node pairs, for node 4, from
which the first order mutants will be combined.
The way of combining the pre-n and post-n mutants
defines the two strategies under this category. The
DomF strategy combines the first mutant of node n
ICSOFT 2010 - 5th International Conference on Software and Data Technologies
326

with the first unselected mutant of the first post-n
node, the second with the first unselected of the first
of the pre-n node etc. The process continues until all
mutants of node n have been used at least once and
one mutant from every pre-n and post-n nodes has
also been selected. The strategy DomDiff selects the
mutants in a similar fashion with an additional
restriction of selecting mutants produced by different
mutation operators only.
The Relaxed Dominator category selects mutant
pairs with the same scheme with the Dominator
strategy but in a relaxed way. That is, without
requiring the selection of at least one mutant from
every pre-n and post-n nodes. Thus, the strategies of
this category select one mutant pair for each mutant
belonging to node n and use each mutant as few
times as possible. This means that node pairs shown
in Figure 1, will be generated only if both their
nodes have unused mutants. In a different case the
next available pair that meets the above requirement
will be used.
The strategies RDomF and RDomDiff are the
relaxed versions of the DomF and DomDiff
strategies respectively.
The Strict Dominator category restricts the
selection of mutants among dominated node pairs.
That way it is expected that both or none of the
mutants will be executed by the test cases. The
developed strategies SDomF, SDomDiff use the
same selection approach applied only on the
dominated node sets as described above. It has been
found that by using such a technique many mutants
remain unused as they refer to nodes not being
dominated. For these mutants the appropriate
relaxed dominator strategy has also been used, i.e. if
the SDomF strategy is applied then the unused
mutants will be combined with the RDomF strategy.
4 EXPERIMENT
In the present study we investigated the
effectiveness of various second order strategies and
weak mutation as opposed to strong mutation.
Furthermore the ability of fulfilling strong mutation
while aiming at second order on the one hand and
also similarly when aiming at weak mutation on the
other is analysed.
For the purposes of the experiment a set of 15
Java program test units was used, which were
chosen from those used in (Papadakis et al., 2010)
and (Polo et al., 2009) and an automated framework
was implemented for producing second order and
weak mutation mutants for java. The framework
uses the mujava mutation testing tool (Ma et al.,
2005) for the generation of first order mutants. The
experiment was initiated by independently applying
each one of the second order and weak mutation
testing strategies on all test subjects. Then a
comparison was made based on strong mutation,
which was done by recording the collateral strong
mutation score achieved by the constructed test sets
per each strategy. To eliminate any bias introduced
by a particular test case set, we generated 10
separate test sets for each unit and for each variant.
5 RESULTS
The conducted study tries to unveil details about the
benefits of either using second order mutation
testing strategies or weak mutation instead of strong
mutation.
Table 1 summarizes the achieved equivalent
mutant reduction for all considered strategies (table
columns) and selected units with respect to strong
mutation. The most interesting aspect of this table is
that both second order and weak mutation testing
strategies produce by far less equivalent mutants
than what strong mutation does. The strong mutation
collateral scores for the produced tests of the
considered strategies are shown in Figure 2. It is
obvious that strict category strategies are more
effective than the Dom and RDom strategies.
Additionally, it can be observed that strategies based
on different operators are less effective but as they
produce less equivalent mutants (Table 1) they may
be a good choice.
Conclusively, the experiment suggests that
considerable savings can be achieved by both second
order and weak mutation strategies as opposed to
strong mutation. Weak mutation achieves on average
a score of 97.05% thus, recording approximately an
effectiveness loss of 3% with an achieved reduction
of 27.03% of equivalent mutants (reducing their
number by 73%). This being a very important
observation as it indicates that a 73% less manual
effort (equivalent mutant identification) can be
gained. According to the SDomF strategy a similar
conclusion can be argued as 3.5% of effectiveness
loss, the gain of less equivalent mutants rises to
87%. These results suggest that it is possible to
perform mutation with reasonable resources.
MUTATION TESTING STRATEGIES - A Collateral Approach
327
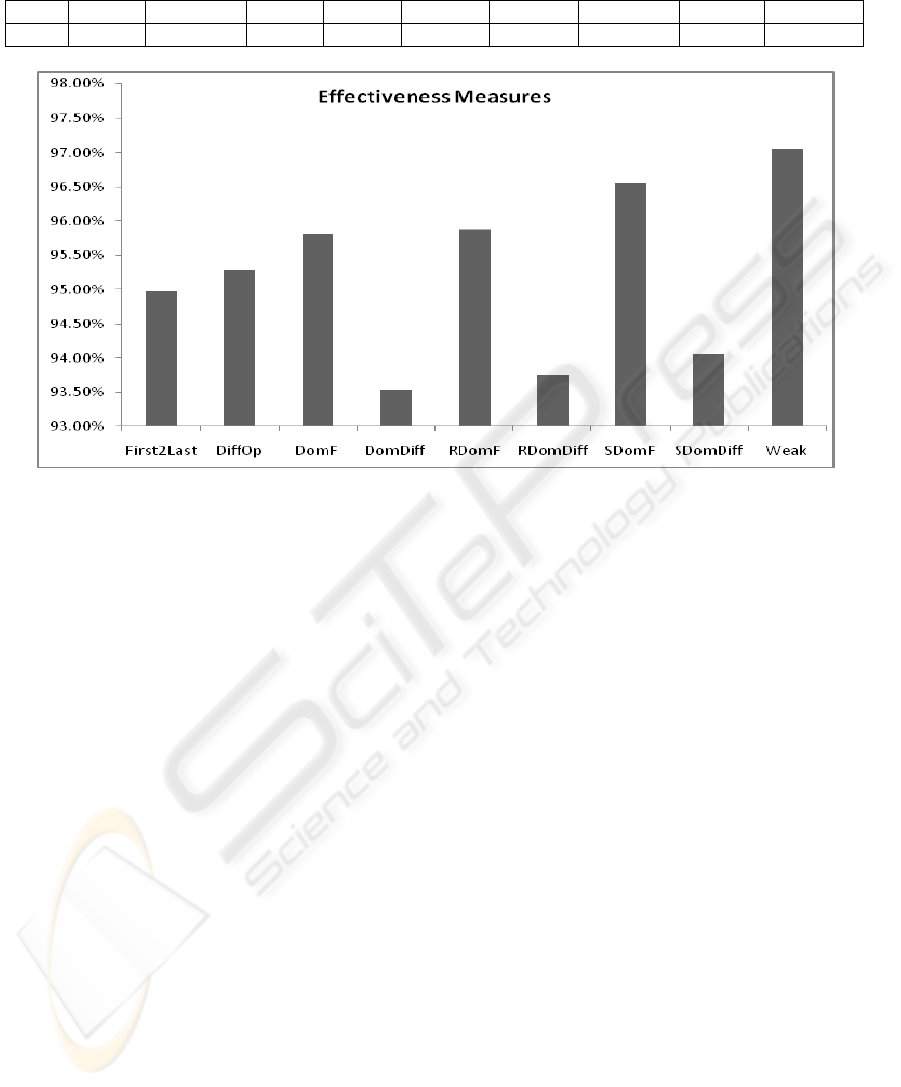
Table 1: Achieved equivalent mutant reduction per strategy with respect to strong mutation.
Unit Weak First2Last DiffOp DomF DomDiff RDomF RDomDiff SDomF SDomDiff
Total 72,97% 91,22% 92,91% 83,78% 92,23% 85,47% 91,89% 86,82% 94,93%
Figure 2: Achieved collateral strong mutation scores of the considered strategies.
6 CONCLUSIONS
This paper presents an experiment on mutation
testing strategies. The conducted experiment tried to
empirically examine the advantages and
disadvantages of using second order and weak
mutation testing strategies. The results indicate that
second order mutation testing strategies form a
viable alternative to strong mutation as they can
achieve considerable effort savings, without a
significant loss on their collateral coverage.
REFERENCES
Agrawal, H. 1994. Dominators, super blocks, and program
coverage. Proceedings of the 21st ACM SIGPLAN-
SIGACT symposium on Principles of programming
languages. Portland, Oregon, United States: ACM.
Andrews, J. H., Briand, L. C., Labiche, Y. & Namin, A. S.
2006. Using Mutation Analysis for Assessing and
Comparing Testing Coverage Criteria. IEEE Trans.
Softw. Eng., 32, 608-624.
Demillo, R. A., Lipton, R. J. & Sayward, F. G. 1978. Hints
on Test Data Selection: Help for the Practicing
Programmer. Computer, 11, 34-41.
Hamlet, R. G. 1977. Testing Programs with the Aid of a
Compiler. IEEE Trans. Softw. Eng., 3, 279-290.
Howden, W. E. 1982. Weak Mutation Testing and
Completeness of Test Sets. IEEE Trans. Softw. Eng.,
8, 371-379.
Kintis, M. 2010. Mutation testing and its approximations.
Master Thesis (in Greek), Athens University of
Economics and Business.
MA, Y.-S., Offutt, J. & Kwon, Y. R. 2005. MuJava: an
automated class mutation system: Research Articles.
Softw. Test. Verif. Reliab., 15, 97-133.
Malevris, N. & Yates, D. F. 2006. The collateral coverage
of data flow criteria when branch testing. Information
and Software Technology, 48, 676-686.
Offutt, A. J. & Lee, S. D. 1994. An Empirical Evaluation
of Weak Mutation. IEEE Trans. Softw. Eng., 20, 337-
344.
Offutt, A. J. & Untch, R. H. 2001. Mutation 2000: uniting
the orthogonal. Mutation testing for the new century.
Kluwer Academic Publishers.
Papadakis, M. & Malevris, N. 2010. An Empirical
Evaluation of the First and Second Order Mutation
Testing Strategies. Proceedings of the 5th
International Workshop on Mutation Analysis
(MUTATION'10). Paris, France.
Papadakis, M., Malevris, N. & Kallia, M. 2010. Towards
Automating the Generation of Mutation Tests. AST
2010. Cape Town.
Polo, M., Piattini, M. & García-Rodríguez, I. 2009.
Decreasing the cost of mutation testing with second-
order mutants. Software Testing, Verification and
Reliability, 19, 111-131.
ICSOFT 2010 - 5th International Conference on Software and Data Technologies
328
