
The Analysis of Resource Constrained Workflows
using Petri Nets
Oana Otilia Prisecaru
Faculty of Computer Science, ”Al. I. Cuza” University
Gen. Berthlot St, No 16, 740083 Iasi, Romania
Abstract. A workflow describes a complex process that takes place inside an
organization. A workflow can be structured into several perspectives. In order to
model both the process and the resouce perspective of workflows, a Petri net
model based on nested Petri nets has been proposed: resource workflow nets
(RWF-nets). Unlike other models, RWF-nets permit a clear distinction between
the perspectives, modelling efficiently their interaction, and ensure the flexibility
of the system. A case (or workflow instance) is the subject of the operations in
the workflow. RWF-nets permit the handling of one case at a time. This paper ex-
tends the definition of RWF-nets in order to allow the handling of multiple cases
at a time, defines a notion of behavioural correctness for RWF-nets, k-soundness,
and proves the decideability of this property for a special class of RWF-nets.
1 Introduction
A workflow is a complex process, consisting of activities organized in order to accom-
plish some goal. A workflow is structured into several perspectives, among which we
mention: the process perspective - specifies which tasks need to be executed and in
what order; the resource perspective - specifies the population in which the workflow
is executed (the resources) and the existing roles (resource classes based on organiza-
tional or functional aspects). A workflow management system (WFMS) is a software
system that supports the modelling and execution of workflows. WFMS’s can use dif-
ferent modelling languages for the definition of workflows. A formal method which
has been successfully used for workflow modelling is Petri nets. Most of the current
research has focused on the modelling of the process perspective of workflows. A Petri
net model for workflows, which includes resources, can be found in [3,4] where special
places are used for representing resources in the process perspective. While no alloca-
tion mechanisms are represented, this approach defines and studies a soundness notion
for workflows. A more detailed view on the resource perspective is offered in papers
like [10,14], where coloured Petri nets are used in order to model a work distribution
system. The approach in [7] allows the modelling of resources and the handling of sev-
eral cases; In [13], resource-extended stochastic workflow nets allow the performance
analysis of the workflows. None of these approaches study the logical correctness of
the workflows. Thus, the existing approaches either model the resource perspective in a
simplistic manner, or they fail to solve verification problems for workflows. Also, there
Otilia Prisecaru O.
The Analysis of Resource Constrained Workflows using Petri Nets.
DOI: 10.5220/0003014900500059
In Proceedings of the 8th International Workshop on Modelling, Simulation, Verification and Validation of Enterprise Information Systems (ICEIS 2010), page
ISBN: 978-989-8425-12-6
Copyright
c
2010 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

is an unclear mixture of perspectives, which can make workflow specifications difficult
to understand, analyze and work with. In order to tackle these problems, in [11, 12], we
proposed a special class of nested Petri nets - Resource Workflow Nets (RWF-nets), for
the integrated modelling of the process and of the resource perspective of workflows.
Nested Petri nets ([8]) are a special class of the Petri net model, in which tokens may
be nets themselves (object-nets). RWF-nets are defined as a special case of two-level
nested Petri nets, in which the two perspectives are modelled as two separate object-
nets: one object-net is a Petri net which models the resource perspective and the other is
a Petri net which models the process perspective. The process perspective is modelled
using extended workflow nets, an extension of workflow nets, introduced in [1]. The
resource perspective is modelled using resource nets, a Petri net model which describes
the existing resources and roles, the allocation of resources to specific roles (accord-
ing to predefined rules) and the release of resources from roles. The two object-nets
synchronize whenever a task from the workflow net uses a role of the resource net and
they behave independently otherwise. A RWF-net describes the handling of one case
at a time, where a case is the subject of the operations in the workflow . A notion of
behavioural correctness was defined and proved decidable for RWF-nets.
In workflow management systems several instances of a workflow (cases) are exe-
cuted simultaneously, hence it is important to verify if the soundness criteria are also
met in this situation. In this paper we extend the definition of RWF-nets in order to
allow the handling of several cases at a time and we define the notion of k-soundness
in order to describe the correct behaviour of RWF-nets for this situation. We prove that
in the case the resource net is live, the k-soundness of the RWF-net is equivalent with
the k-soundness of the extended workflow net and thus, decidable.
The remainder of the paper is organized as follows: Section 2 introduces the def-
inition of resource nets and RWF-nets, Section 3 defines and studies the k-soundness
property for RWF-nets and Section 4 concludes the paper.
2 The Modelling of the Resource Perspective using Petri Nets
2.1 Preliminaries
In what follows we will give the basic terminology and notation concerning workflow
nets, a Petri net formalism which has been used for modelling the process perspective
of workflows (for details the reader is referred to [1]). We assume the reader is familiar
with the Petri net terminology and notation. A workflow net (WF-net) is a Petri net
which has two special places: one source place, i, and one sink place, o. The marking in
which there are k tokens in the source place represents the beginning of the processing
for k cases (the initial marking of the net, denoted by i.k). The marking in which there
are k tokens in the sink place, represents the end of the processing for the k cases (and
the final marking of the net, denoted by o.k). An additional requirement is that every
element of the workflow net should be on a path from i to o.
A Petri net PN=(P,T,F) is a WF-net iff: (1) PN has a source place i and a sink place
o such that •i = ∅ and o• = ∅. (2) If we add a new transition t
∗
to PN such that
•t
∗
= {o} and t
∗
• = {i}, then the resulting Petri net is strongly connected.
51

A marking of a Petri net (and of a WF-net) is a multiset m : P → IN (where IN
denotes the set of natural numbers). We write m = 1
′
p
1
+ 2
′
p
2
for a marking m with
m(p
1
) = 1, m(p
2
) = 2 and m(p) = 0, ∀p ∈ P − {p
1
, p
2
}. The empty marking is
denoted by 0.
We will present the Petri net model used for describing the resource perspective,
defined in [11, 12]. The resource perspective defines the existing resources and their
interaction with the process perspective. A task that needs to be executed for a specific
case is called a work item. Each work item should be performed by a resource suited
for its execution. In order to facilitate the better allocation of resources to work items,
resources are grouped into roles. Thus, instead of assigning work items directly to re-
sources, work items will be assigned to certain roles. This way (pattern) of representing
and using resources is called ”role-based allocation” ([6,9, 14]).
A role, also referred to as a resource class, is a group of resources with similar
characteristics. We consider that each resource has a general type. A resource can have
more roles (at different moments in time) and each role can be performed by several
resources of different types ([6]).
In our model, for each role one must specify the set of resource types that can be
mapped onto that role. Based on these rules (which are specified at design time), the
system will be able to allocate dynamically resources to the appropriate roles. Thus, a
specification for the resource perspective consists in the following elements:
- A set of resource basic types: RT = {T ype
1
, . . . , T ype
n
}. For each type T ype
i
, i ∈
{1, 2, . . . , n} there is a number n
i
of resources of that type.
- A set of roles, RO = {Rol e
1
, Role
2
, . . . , Role
m
}.
- For each role r ∈ RO, res(r) represents the resource types which can be assigned to
the role (res(r) ⊆ RT ).
Given the elements above, a resource net RN = (P
RN
, T
RN
, F
RN
) can be defined
as follows:
– P
RN
= P
RT
∪ P
ROLE
∪ P
′
where: P
RT
= RT , P
ROLE
= RO and P
′
= {R
ki
|Role
i
∈
RO, T ype
k
∈ res (Role
i
)}.
– T
RN
= {assign
ki
, release
ik
|Role
i
∈ RO, T ype
k
∈ res(Role
i
)} ∪ T
Rem
, where T
Rem
is a set of transitions which can remove resources.
– F
RN
= {(T ype
k
, assign
ki
), (assign
ki
, Role
i
), (assign
ki
, R
ki
), (R
ki
, release
ik
),
(Rol e
i
, release
ik
), (release
ik
, T ype
k
)|Role
i
∈ RO, T ype
k
∈ res(Role
i
)} ∪ F
Rem
,
where F
Rem
⊆ P
RT
× T
Rem
.
In the resource net, P
RT
corresponds to the set of resource types and P
ROLE
corre-
sponds to the set of roles. For each role Role
i
and for each resource type T yp e
k
∈
res (Role
i
) the following elements are added to the net (see Fig. 1): a place R
ki
, which
will be used for the proper release of resources; a transition assign
ki
which moves a
resource from T ype
k
to role Role
i
; a transition release
ik
which releases the resources
of type T ype
k
, assigned to Role
i
, when they are not needed any longer. In the initial
marking of the net, in every place T ype
i
, there will be a number of tokens equal to
the number of resources of that type. The transitions in the set T
Rem
can model the
situation in which certain resources become permanently unavailable in the workflow.
One can notice that the Petri net model we propose abstracts from the interaction
with the process perspective. In the Petri net model which integrates both perspectives,
52
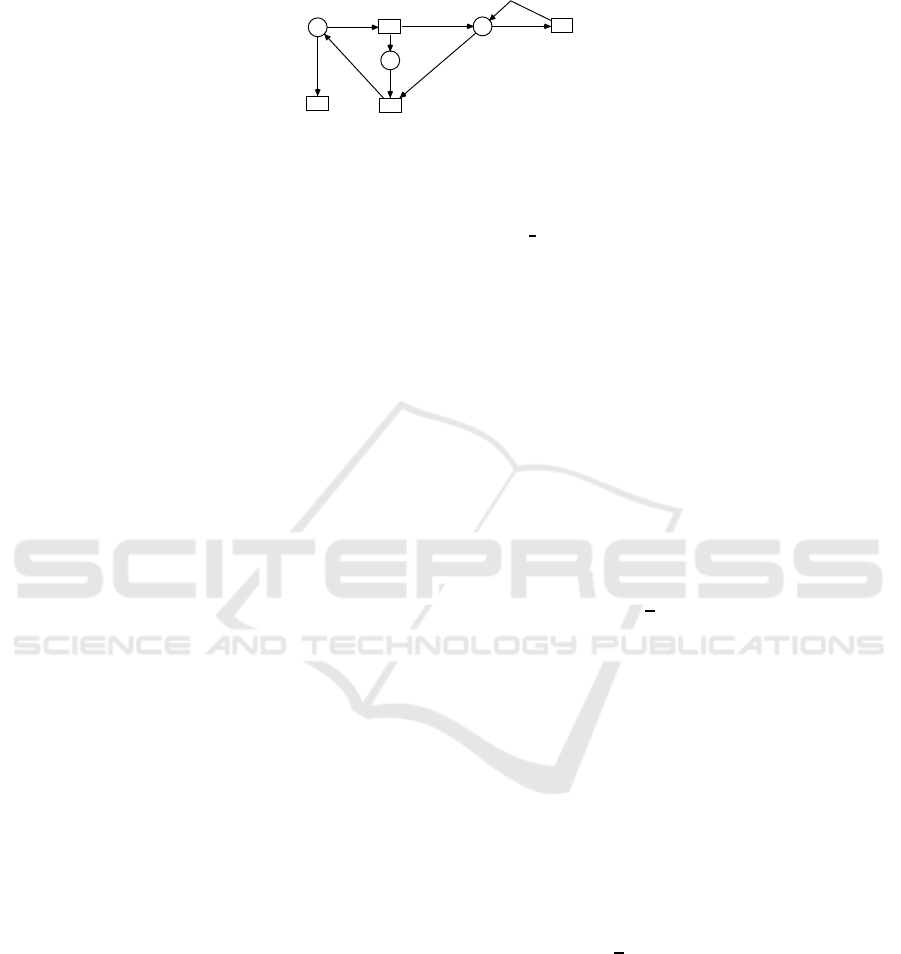
Type_k
release_ik
R_ki
exec_task
Role_iassign_ki
t_rem
Fig.1. A resource workflow net in its initial marking.
for every task in the workflow that needs the role Role
i
for its execution, a new transi-
tion will be added to the resource net (transition exec task in Fig. 1).
Let W F = (P, T, F ) be a WF-net. The extended WF-net is W F
′
= (P, T
′
, F
′
),
where: T
′
= T ∪ {t
′
} and F
′
= F ∪ {(o, t
′
)}.
2.2 Resource Workflow Nets
In what follows we will define resource workflow nets (RWF-nets). We will extend our
approach from [11, 12], in order to allow the handling of several cases simultaneously
in the workflow. RWF-nets will be defined as a special class of nested Petri nets, in
which there exist only two object-nets, together with a function Role. Nested Petri nets
are Petri nets which can have as tokens ordinary Petri nets. A nested Petri net consists
of a system net (a high level Petri net with expressions on arcs) and object Petri nets.
Definition 1. A Resource Workflow Net is a two-level nested Petri net together with a
function Role: RW F N = (V ar, Lab, (W F
′
, i.k), (RN, rm
0
), SN, Λ, Role):
1. V ar = {x, y} is a set of variables.
2. Lab = Lab
h
∪ Lab
v
is a set of net labels such that Lab
v
= {e, e}.
3. (W F
′
, i.k), (RN, rm
0
) are object-nets: (W F
′
, i.k) is an extended WF-net with its
initial marking and (RN, m
0
) is an extended resource net with its initial marking.
4. SN = (N, W, M
k
0
) is the system net of RWFN, such that:
- N= (P
N
, T
N
, F
N
) is a high level Petri net such that:
- P
N
= {I, p, O} , where O is a place such that O• = ∅ and I
is a place such that •I = ∅.
- T
N
= {end}.
- F
N
= {(I, end), (p, end), (end, p), (end, O)}.
- M
k
0
is the initial marking of the net, in which there exist k atomic tokens in place
I, place p contains the pair ((W F
′
, i.k), (RN, m
0
)) and place O is empty.
- W is the arc labelling function: W (I, end) = 1, W (p, end) = W (end, p) =
(x, y), W (end, O) = 1.
5. Λ is a partial function which assigns to certain transitions from the nets W F
′
, RN,
SN, a label from the set Lab, and: Λ(end) = e, Λ(t
′
) = e. For any transition t
in W F
′
, t 6= t
′
, such that Λ(t) is defined, there is a transition t
r
∈ T
RN
such that
Λ(t) = Λ(t
r
) ∈ Lab
h
.
6. Role is a partial function which assigns to every labelled transition t from W F
′
(t 6= t
′
) a role from RN such that: if Λ(t) = l and Role(t) = Role
i
then there
exists t
∗
in RN with Λ(t
∗
) = l and (t
∗
, Role
i
), (Role
i
, t
∗
) are arcs in RN .
53

There are two object-nets in a RWFN-net: (W F
′
, i.k) is an extended WF-net which
models the process perspective and (RN, rm
0
) describes the resource perspective: RN
is a resource net to which some labelled transitions are added in order to ensure the
interaction with the process perspective. Variables x and y will be assigned certain
values at runtime: the possible values for these variables are the object-nets (in certain
markings). x has the net type W F
′
and y has the net type RN . In SN, the places I
and O will hold atomic tokens, while p will hold a pair of net-tokens. There is only
one constant, 1, for the arcs (I, end), (end, O), which is interpreted as an atomic token.
Role is a partial function which assigns to every task (labelled transition) t in W F , a
role Role
i
from RN . This function designates the role that can execute this task. Λ is
a partial function which labels the transitions of the object-nets and of the system-net.
If t is a labelled transition in W F
′
, t 6= t
′
and t needs a role Role
i
for its execution
(i.e. Role(t) = Role
i
), then there exists a corresponding transition in RN , connected
to Role
i
with the same label as t. Also, t
′
and end have complementary labels.
A workflow is modelled using RWF-nets in the following manner: first, the pro-
cess perspective is modelled using an extended WF-net. The resource perspective is
modelled separately using a resource net. For each task that needs a certain role for its
execution, a new transition is connected with the place corresponding to that role, in the
resource net. The task and the added transition have the same label.
We denote by A
net
the set of net-tokens (marked object-nets): A
net
= {(EN, m)|
EN ∈ {W F
′
, RN }, m is a marking of EN}. A marking of a resource workflow net
can be represented as a vector M = (M (I), M (p), M(O)), where M (I), M (O) ∈ N
and M(p) ∈ N
A
2
net
. A binding b for the transition end is a function b : {x, y} → A
net
.
b assigns net-tokens to the variables of the net. Transition end from the system net SN
of a RWF-net is enabled in a marking M w.r.t. a binding b if I contains at least an
atomic token and W (p, end)(b) = (x, y)(b) = (b(x), b(y)) ∈ M(p).
The steps that can occur in resource workflow nets are those defined for two-level
nested nets ([8]): The firing of am unlabelled transition, which is enabled in the mark-
ing of RN or of W F
′
, represents an object-autonomous step; A labelled transition
enabled in the marking of W F
′
should fire at the same time with a transition with
the same label enabled in the marking of RN . The simultaneous firing of these two
transitions represents a horizontal synchronization step. In the resulting marking of the
RWF-net, both the marking of W F
′
and R N will change; If end is enabled in SN w.r.t.
a binding b and t
′
is enabled in W F
′
, the synchronous firing of end and t
′
represents
a vertical synchronization step. The firing of the vertical synchronization step in a cer-
tain binding b (b(x) = (W F
′
, m), b(y) = (RN, rm)) removes the pair of net-tokens
((W F
′
, m), (RN, rm)) from place p and then adds back to p the pair of net-tokens :
((W F
′
, m
′
), (RN, rm)), where m
′
is the marking obtained in W F
′
by firing the tran-
sition t
′
. An atomic token will be added to place O.
The set of all steps in a RWF-net is denoted by Y.
The example in Fig. 2 presents a RWF-net modelling a workflow which processes
admission applications for a college. There are two types of resources (assistants and
professors) and two possible roles: secretary (S) and commission member (CM). A S
role can be performed by an assistant and a CM role can be performed by a profes-
sor. The specification for the resource perspective is: RT = { assistants ,professors},
54

l1
l2
R2
release_CM
l1
l3
l4
t’
end
e
p1
p2
send_answer
l3
o
l2
assign_CM
SN
exec2
exec3
exec1
R1
assign_S
exec4
( )
I
O
reject
RN
l4
WF’
accept
e
CM
S
assistants
release_S
register_application
p
(x,y)
(x,y)
i
professors
Fig.2. A resource workflow net in its initial marking.
RO = {S, CM }, res(S)={assistants}, res(CM)={professors}. The function Role de-
scribes which roles must execute the tasks of the workflow and it is defined as follows:
Role(register application)=S,Role(accept)=CM, Role(reject)=CM, Role(send answer)
=S. The marking m
0
for RN is: m
0
= 1
′
assistants + 1
′
prof essors. In the initial
marking of the RWF-net, M
0
(I) = 1, M
0
(p) = ((W F
′
, i.1), (RN, m
0
)). In M
0
, tran-
sition register application from W F
′
cannot fire, although it is enabled in (W F
′
, i.1):
it can only fire simultaneously with transition exec1 in RN , which is not enabled. As-
sume the object-autonomousstep (; as sign S) fires first. The new marking of the RWF-
net is M
1
= (1, ((W F
′
, i.1), (RN, m
1
)), 0), where m
1
= 1
′
S +1
′
R
1
+1
′
prof essors.
The step (register application, e xec 1) is enabled in M
1
, producing a new marking
(see Fig. 2) M
2
= (1, ((W F
′
, m
′
1
), (RN, m
2
)), 0), where m
′
1
= 1
′
p
1
and m
2
=
m
1
. The system remains blocked (no other task in the process is executed) until re-
sources (assistants) are allocated for the CM role. Transition assign CM can fire in-
dependently in RN. The resulting marking is M
3
= (1, ((W F
′
, m
′
1
), (RN, m
3
)), 0),
where m
3
= 1
′
S + 1
′
CM + 1
′
R
2
+ 1
′
R
1
. In M
3
, the step (accept,exec2) can fire
and the resulting marking is M
4
= (1, ((W F
′
, m
′
2
), (RN, m
4
)), 0) where m
′
2
= 1
′
p
2
and m
4
= m
3
. Next, the step (send answer,exec4) can fire producing the marking
M
5
= (1, ((W F, m
′
3
), (RN, m
5
)), 0) where m
5
= m
4
and m
′
3
= 1
′
o. The verti-
cal synchronization step Y = (end; t
′
) is enabled in marking M
5
with the binding b:
b(x) = (W F, m
′
3
), b(y) = (RN, m
5
) and the firing of this step produces the marking
(0, ((W F
′
, 0 ), (RN, m
5
), 1)) which corresponds to the correct processing of the case.
3 The k-Soundness of Resource Workflow Nets
In this section we will introduce a notion of k-soundness for RWF-nets.
A notion of k-soundness was defined for WF-nets, expressing the minimal condi-
tions a correct workflow should satisfy ([3,5]). We consider that an extended workflow
net W F
′
is sound if the underlying WF-net is sound.
A workflow net W F = (P, T, F ) is k-sound iff: (1) for every marking m reach-
able from the initial marking i.k, there exists a firing sequence leading from m to the
55

final marking o.k (termination condition): (∀m)((i[∗im) =⇒ (m[∗io)); (2) All the
transitions in W F are quasi-live:(∀t ∈ T )(∃m, m
′
)(i.k[∗im[tim
′
).
It was proven ([5]) that, if W F is k-sound: (m ∈ [i.ki) ∧ m ≥ o.k) ⇒ (m = o.k).
The following result can be easily proven:
Lemma 1. Let RW F N be a RWF-net and M ∈ [M
k
0
i a reachable marking. Then
M = (k
1
, ((W F
′
, m), (RN, rm)), k
2
), where m is a reachable marking in W F
′
and
rm is a reachable marking in RN .
Let RW F N be a RWF-net. If the initial marking is M
k
0
, the set of final markings for
RW F N is: M
f
k
= {(0, ((W F
′
, 0 ), (RN, rm)), k)|rm is a reachable marking of RN}.
We will consider that a RWF-net is k-sound if: (1) W F
′
is k-sound, (2) for any
reachable marking of the RWF-net, M ∈ [M
k
0
i, there is a firing sequence that leads to
a final marking M
f
(the termination property) and (3) all the steps in the RWF-net are
quasi-live.
Definition 2. A RWF-net RW F N is k-sound if and only if:
1. (W F
′
, i.k) is a k-sound extended workflow net.
2. For every marking M reachable from the initial marking M
k
0
, there exists a firing
sequence leading from M to a final marking M
f
:
(∀M)((M
k
0
[∗iM ) =⇒ (M[∗iM
f
, M
f
∈ M
f
k
).
3. RW F N is quasi-live: ∀Y ∈ Y, there exists a marking M ∈ [M
0
i such that M [Y i.
First, we consider the workflow is k-sound if the WF-net describing the process is k-
sound (abstracting from resources). A final marking of the RWF-net is reached if the
vertical synchronization step fires k times. This implies that transition t
′
can fire k times
in W F
′
, which happens if and only if the final marking of the WF-net can be reached.
Thus, condition (2) states that the workflow is k-sound if the termination condition still
holds in the WF-net, when the firing of tasks is restricted by the resource perspective.
Lemma 2. Let RW F N be a RWF-net such that W F
′
is k-sound. The markings in
M
f
k
are the only markings reachable from M
k
0
which contain k tokens in place O:
(∀M)((M
k
0
[∗iM ) ∧ M (O ) = k) =⇒ (M ∈ M
f
k
)).
Proof. Let M ∈ [M
k
0
i with M(O) = k. Tokens can be added to place O only by the
firing of the vertical synchronizationstep (end; t
′
). In order to produce k tokens in place
O, this step has to fire k times. Since M
0
[∗iM , then m ∈ [i.ki
W F
′
and rm ∈ [rm
0
i
(Lemma 1). Thus, ∃ σ ∈ T
′∗
such that i.k[σim. t
′
has k occurrences in σ. Since
o• = {t
′
}, the order in which the transitions t
′
appears in σ is not important. Thus, we
can write σ = σ
′
(t
′
)
k
, σ
′
∈ T
∗
. Hence, i.k[σ
′
im
′
[(t
′
)
k
im. m
′
(o) = k. Since W F
is k-sound, the only reachable marking with k tokens in o is o.k . If o.k[(t
′
)
k
im, then
m = 0. Also, because M(I) + M(O) = k and M(O) = k, it results that M (I) = 0.
Thus, M ∈ M
f
k
.
Lemma 3. Let RW F N = (V ar, Lab, (W F
′
, i.k), (RN, rm
0
), SN, Λ, Role) be a RWF-
net such that W F
′
is k-sound and (RN, rm
0
) is live. Then, for every reachable mark-
ing m ∈ [i .ki in W F
′
, there is a reachable marking M ∈ [M
k
0
i in RW F N such that
M = (k
1
, ((W F
′
, m), (RN, rm)), k
2
), where rm ∈ [rm
0
i.
56

Proof. Let m ∈ [i.ki be a reachable marking in W F
′
. Then, there is a sequence of tran-
sitions in W F
′
, σ ∈ T
′∗
, such that i.k[σim. Let |σ| = n. We will prove, by induction
on n, that there exists a sequence of steps in RW F N , σ
′
∈ Y
∗
, such that M
k
0
[σ
′
iM
and M = (k
1
, ((W F
′
, m), (RN, rm)), k
2
), where rm is a reachable marking in RN.
Base. If n = 0, then m = i.k. If we consider σ
′
the empty sequence of steps in
RW F N , then M
k
0
[σ
′
iM
k
0
, M
k
0
= (k, ((W F
′
, i.k), (RN, rm
0
)), 0).
Step. Assume the property holds for n and we prove it for n + 1: If i.k[t
1
. . . t
n
i
m
′
[t
n+1
im, for the sequence i.k[t
1
. . . t
n
im
′
, there is a sequence of steps in RW F N
such that M
k
0
[Y
1
. . . Y
s
iM
′
, where M
′
= (k
′
1
, ((W F
′
, m
′
), (RN, rm
′
)), k
′
2
) and rm
′
∈
[rm
0
i.
(1) If t
n+1
is an unlabelled transition in W F
′
: the result follows easily, considering
then the object-autonomous step Y = (; t
n+1
) in RW F N from the marking M
′
.
(2)If t
n+1
6= t
′
is a labelled transition in W F
′
, then there exists t
′
n+1
in RN
such that λ(t
n+1
) = λ(t
′
n+1
). If t
′
n+1
is not enabled in rm
′
in RN , because t
′
n+1
is live, there exists rm
′′
∈ [rm
′
i such that: rm
′
[t
′
1
. . . t
′
m
irm
′′
[t
′
n+1
irm. We can as-
sume there are no labelled transitions in this sequence (the labelled transitions do not
have any effect on markings so they can be removed from the sequence). We can con-
sider the following steps: Y
′
1
= (; t
′
1
), . . . , Y
′
m
= (; t
′
m
). Thus, M
′
[Y
′
1
. . . Y
′
m
iM
′′
,
where M
′′
= (k
′
1
, ((W F
′
, m
′
), (RN, rm
′′
)), k
′
2
). Y = (t
n+1
; t
′
n+1
) is enabled in M
′′
:
M
k
0
[Y
1
. . . Y
s
i M
′
[Y
′
1
. . . Y
′
m
i M
′′
[Y iM , where M = (k
′
1
, ((W F
′
, m), (RN, rm)), k
′
2
)
and rm ∈ [rm
0
i.
(3) If t
n+1
= t
′
, t
′
is enabled in marking m
′
in W F
′
. We prove that the verti-
cal synchronization step Y = (end[b]; t
′
) is enabled in M
′
with the binding b(x) =
(W F
′
, m
′
), b(y) = (RN, rm
′
). In order to show that transition end is enabled in M
′
,
we will prove that M
′
(I) > 0. Assume M
′
(I) = 0. Then, it results that M
′
(O) = k.
From Lemma 2, it results that m
′
= 0, which contradicts the fact that t
′
is enabled in
W F
′
. Thus, M
k
0
[Y
1
. . . Y
s
i(k
′
1
, ((W F
′
, m
′
), (RN, rm
′
)), k
′
2
)[(end[b]; t
′
)i
(k
′
1
− 1, ((W F
′
, m), (RN, rm
′
)), k
′
2
+ 1).
Let (W F
′
, i.k) be a k-sound extended WF-net together with its initial marking. It
can be easily proven that all the transitions in W F
′
are quasi-live.
Lemma 4. Let RW F N be a RWF-net such that W F
′
is k-sound and (RN, rm
0
) is
live. All the steps in RW F N are quasi-live: ∀Y ∈ Y, ∃M ∈ [M
k
0
i such that M[Y i.
Proof. W F
′
is k-sound, so all the transitions in W F
′
are quasi-live. (RN, m
0
) is live
hence, all the transitions in RN are quasi-live. Let Y be a step in R W F N . We consider
the following cases:
(1)Y is an object-autonomous step: then Y = (; t) and t is an unlabelled transition
from W F
′
or RN. If t is an unlabelled transition from RN: since t is live in RN , there
is rm ∈ [rm
0
i such that: rm
0
[t
1
. . . t
m
irm[ti. We can consider that t
1
, . . . , t
m
are
unlabelled in RN . The following object-autonomous steps can fire in RW F N from
the initial marking: Y
1
= (; t
1
), . . . , Y
m
= (; t
m
): M
k
0
[Y
1
. . . Y
m
iM, where M =
(k, ((W F
′
, i.k), (RN, rm)), 0). The step Y = (; t) is enabled in M , because rm[ti in
RN . If t is an unlabelled transition from W F
′
: similar to the previous case.
(2)Y is a horizontal synchronization step: similar to (1).
57

(3) If Y is the vertical synchronization step: Y = (end; t
′
). t
′
is quasi-live in
W F
′
, so there is m ∈ [i.ki such that m[t
′
i. For m ∈ [i.ki, there exists M ∈ [M
k
0
i,
M = (k
1
, ((W F
′
, m), (RN, rm)), k
2
). Also, M (I) 6= 0 (otherwise, from Lemma 2,
M ∈ M
f
k
and m = 0 ). Now, if we consider the binding b with b(x) = (W F
′
, m) and
b(y) = (RN, rm), then end is enabled in marking M w.r.t. binding b and M[en d(b); t
′
i.
The following theorem shows that in a RWF-net in which the resource net RN is
live, the k-soundness is equivalent with the k-soundness of its workflow net, which is a
decidable property ([3,4]):
Theorem 1. LetRW F N = (V ar, Lab, (W F
′
, i), (RN, rm
0
), SN, Λ, Role) be a RWF-
net such that (RN, rm
0
) is a live resource net. Then, RW F N is k-sound if and only if
W F
′
is k-sound.
Proof. (=⇒) If RW F N is k-sound, W F
′
is k-sound.
(⇐=) If W F
′
is k-sound, the first condition in the definition of soundness for RWF-
net takes place.Also, RW F N is quasi-live: because (RN, rm
0
) is live and W F
′
is
k-sound, using Lemma 4, it results that RW F N is quasi-live.
We will show that the second condition in the definition of RWF-nets also takes
place: Assume M ∈ [M
k
0
i, M = (k
1
, ((W F
′
, m), (RN, rm)), k
2
). There exists τ ∈
Y such that M
0
[τiM . k
2
is the number of ocurrances of the vertical step (end; t
′
)
in τ . k
1
+ k
2
= k. We can write τ = τ
′
(end; t
′
)
k
2
and M
0
[τ
′
iM
′
[(end; t
′
)
k
2
iM.
M
′
= (k, ((W F
′
, m
′
), (RN, rm)), 0) and m = m
′
− o.k
2
. Using Lemma 1, it results
that there exists a transition sequence σ in W F
′
such that i.k[σim
′
(σ does not contain
the transition t
′
). Because W F
′
is k-sound, there is a transition sequence σ
′
such that
m
′
[σ
′
io.k. σ
′
does not contain t
′
and σ
′
can also fire from m = m
′
− o.k
2
(o does not
haveoutput transitions in σ
′
). m[σ
′
i(o.k−o.k
2
). Let σ
′
= t
1
. . . t
k
and t
i
6= t
′
. We show
there exists a sequence of steps such that M
′
= (k, ((W F
′
, m
′
), (RN, rm)), 0)[∗ i
(k, ((W F
′
, o.k), (RN, rm)), 0). Let Y = (t, t
∗
), with λ(t) = λ(t
∗
). If t
∗
is not en-
abled in r m , since (RN, rm
0
) is live, there exists a sequence of transitions rt
1
. . . rt
k
such that rm[rt
1
. . . rt
k
irm
′
[t
∗
irm
1
. The steps Y
1
= (; rt
1
), . . . Y
k
= (; rt
k
) are
enabled in M
′
and M
′
[Y
1
. . . Y
k
iM
′′
[Y i. Thus, for every transitions t
i
∈ σ
′
from
W F we can obtain a corresponding sequence of steps in RW F N. Finally, we can
obtain a sequence of transitions π such that M
′
[πi (k, ((W F
′
, o.k), (RN, rm
∗
)), 0).
No vertical synchronization step fires in π and π does not remove tokens from o. Also,
no transitions remove tokens from o except t
′
. Thus, π can fire from M and M =
(k
1
, ((W F
′
, m
′
−o.k
2
), (RN, rm)), k
2
)[πi(k
1
, ((W F
′
, o.k −o.k
2
), (RN, rm
∗
)), k
2
).
Now, the vertical synchronization step can fire k − k
1
times producing the final marking
(0, ((W F
′
, 0 ), (RN, rm)), k).
4 Conclusions
This paper presented a special class of nested Petri nets used to model both the re-
source perspective and the process perspective for a workflow, allowing the handling
of k cases at a time. The two perspectives are represented as two independent object-
nets. The advantage of this approach is that it integrates both perspectives but it keeps
58

a clear difference between them: unlike other approaches that use Petri nets ([3, 4,10,
14,7, 13]), resources and roles are not represented in the same Petri net as the process.
A notion of k-soundness was introduced in order to study the logical correctness of
workflows: even if the workflow is 1-sound, when k cases are processed, it is possi-
ble that some cases could not be handled due to insufficient resources. We proved that
k-soundness is decidable for a special class of RWF-nets.
References
1. W. M. P. van der Aalst: The Application of Petri nets to Workflow Management, The journal
of Circuits, Systems and Computers, 8(1): pp. 21- 66, Eindhoven University of Technology,
The Netherlands, 1998.
2. W. M. P. van der Aalst: Verifications of Workflow Nets. P. Azema and G. Balbo, editors,
Application and Theory of Petri nets 1997, volume 1248 of Lecture Notes in Computer
Science, pp. 407-426, SpringerVerlag, Berlin, 1997.
3. K. Barkaoui, L. Petrucci: Structural analysis of workflow nets with shared resources. Work-
flow management: Net-based Concepts, Models, Techniques and Tools (WFM’98), volume
98/7 of Computing science reports, pp. 82-95, Eindhoven University of Technology, 1998.
4. K. van Hee, N. Sidorova, M. Voorhoeve: Resource-Constrained Workflow Nets. Lindemann,
Burkhard, Czaja, Skowron, Schlingloff, Suraj (Eds.): Proc. of the International Workshop
on Concurrency, Specification and Programming (CS & P) 2004, pp. 166-177, Informatik-
Berichte der Humboldt-Universitat zu Berlin, Nr. 170, September 2004.
5. K. Hee, N. Sidorova and M. Voorhoeve: Generalised Soundness of Workflow Nets Is Decid-
able. In Application and Theory of Petri Nets 2004, vol. 3099 of Lecture Notes in Computer
Science, pages 8295. Springer-Verlag, Berlin, 2004 .
6. A. Kumar, W.M.P. van der Aalst, H.M.W. Verbeek: Dynamic Work Distribution in Workflow
Management Systems: How to balance quality and performance?. Journal of Management
Information Systems, 18(3), pp.157-193, 2002.
7. J. Li, Y. Fan, and M. Zhou. Performance modeling and analysis of workflow. IEEE Transac-
tions on Systems, Man, and Cybernetics, Part A: Systems and Humans, 34:229242, 2004
8. I.A. Lomazova: Nested Petri Nets - a Formalism for Specification and Verification of Multi -
Agent Distributed Systems. Fundamenta Informaticae 43 pp. 195-214, 2000.
9. M. zur M¨uhlen. Resource modeling in workflow applications. Proceedings of the 1999 Work-
flow Management Conference (November 1999), pp. 137-153, 1999.
10. M. Netjes, W.M.P. van der Aalst, H.A. Reijers. Analysis of resource-constrained processes
with colored petri nets. In K. Jensen, Proc. of the 6th Workshop and Tutorial on Practical
Use of Coloured Petri nets and the CPN Tools (CPN’05), pp. 251-265, 2005
11. O. Prisecaru. Resource workflow nets:a Petri Net Formalism for Workflow Modelling. In
Proc. of MSVVEIS 2007, pages 1121, 2007.
12. O. Prisecaru. Resource workflow nets: an approach to workflow mod- elling and analysis.
Enterprise Information Systems, 2:101120, 2008.
13. H. A. Reijers. Design and Control of Workflow Processes. Business Process Management for
the Service Industry, volume 2617 of LNCS. Springer-Verlag, Berlin, 2003.
14. I.T.P. Vanderfeesten, W.M.P. van der Aalst, H.A. Reijers. Modelling a product based work-
flow system in CPN Tools. In K. Jensen, Proc. of the 6th Workshop and Tutorial on Practical
Use of Coloured Petri Nets and the CPN Tools, pp. 99-118, Aarhus, Denmark: University of
Denmark, 2005.
59
