PROCESS MODEL VALIDATION

Transforming Process Models to Extended Checking Models

Elke Pulverm¨uller

Department of Computer Science, University Osnabr¨uck, Albrechtstr. 28, D-49076 Osnabr¨uck, Germany

Andreas Speck, Sven Feja, S¨oren Witt

Department of Computer Science, Christian-Albrechts-University Kiel, Olshausenstr. 40, D-24098 Kiel, Germany

Keywords:

Process model validation, Model checking, Model translation and speciﬁers for temporal logic operators.

Abstract:

Process and workﬂow models are typical means to describe the dynamic activities of a system. Therefore,

it is of high interest to validate these models. Many kinds of (business) rules, best practices, patterns, legal

regulations may serve as speciﬁcations which the models have to fulﬁll.

An already established technique to validate models of dynamic activities is model checking. In model check-

ing the requirements are expressed by temporal logic. Temporal logic allows describing temporal depen-

dencies. The models to be veriﬁed by model checkers are automata. In this context the question is how to

transform process or workﬂow models into automata and how to specify the temporal logic in the way that the

semantic of the process models is considered sufﬁciently.

In our paper we present three approach to transform process models to checkable automata. We use the exam-

ple of ARIS Event-driven Process Chains. In particular, the third approach introduces specializers enabling

semantic-rich requirement speciﬁcations. This reduces the gap between process models (consisting of different

model element types) and veriﬁcation models.

1 INTRODUCTION

Workﬂows and processes are fundamental concepts in

computer-based systems. For example real-time sys-

tems as well as large scale business systems are based

on process execution. All the systems have in com-

mon that their dynamic behavior is the essential ele-

ment. Even a simple purchase system has to realize a

selling process.

There exist different modeling concepts for the

different types of systems, e.g. SDL or the model-

ing language Z for time-critical systems or business

process models for commercial systems. These pro-

cess and workﬂow models are potentially subject of

automated veriﬁcation (B´erard et al., 2001). With the

paper we propose a step to close the gap between pro-

cess models and veriﬁcation models to overcome the

loss of semantics due to surjective mappings and, in

consequence, to support the veriﬁcation and testing

(with partial veriﬁcation) in a way which is closer to

the world of the software develop

In the paper we use the business process model

of the modeling concept ARIS (Architecture of inte-

grated Information Systems): the EPCs (Event-driven

Process Chains) (Scheer, 1998) (Scheer and N¨uttgens,

2000). EPCs are mainly used to model commer-

cial and administrative systems. The real application

models we use to demonstrate our approach is a high-

performance e-commerce system: Intershop Enﬁnity

(Intershop Communications AG) (Breitling, 2002).

This e-commerce system is used in large scale sys-

tems of retailers (e.g. Otto), in the automotive branch

(Volkswagen, MAN, BMW) or in e-procurement sys-

tems (run by the German Federal Ministry of the In-

terior or governments of other countries or large com-

panies). Besides the modeling of e-commerce sys-

tems ARIS EPCs are used to model almost all kinds

of commercial information systems, e.g. enterprise

resource planning systems (ERP) like SAP R/3. Orig-

inally ARIS has been developed in cooperation with

SAP AG to support the modeling of the ERP system.

Another interesting application of EPC models is the

description of processes in the administration. Specif-

ically data privacy protection problems are modeled

214

Pulvermüller E., Speck A., Feja S. and Witt S. (2010).

PROCESS MODEL VALIDATION - Transforming Process Models to Extended Checking Models.

In Proceedings of the Fifth International Conference on Evaluation of Novel Approaches to Software Engineering, pages 214-220

DOI: 10.5220/0003016602140220

 SciTePress

in EPCs and then checked. Some alternative models

are the Business Process Modeling Notation (BPMN)

(OMG, 2006) or UML Activity Diagrams.

1.1 EPC Model Elements

As already mentioned the EPC model type is part

of the modeling concept ARIS. The basic elements

of an EPC model are shown in ﬁgure 1: The con-

trol ﬂow is symbolized by a sequence of

events

(ma-

genta hexagons) and

functions

(green rectangles with

rounded edges) which are connected by arrows repre-

senting the control ﬂow. Branches in the control ﬂow

are deﬁned by the Boolean logic operators: AND, OR

and XOR. In the ﬁgure an XOR is depicted. AND re-

quires that all paths of the branches are active. OR in-

dicates that at least one path is used. XOR allows that

one and only one path is chosen. The element type

organizational unit

(rectangle with double line on the

left) is an example for a further element type.

Figure 1: Example of an EPC Model.

1.2 Gap in Checking Models

Our approach is based on the model checking tech-

nology (Clarke et al., 2001a). This kind of veriﬁca-

tion typically takes ﬁnite state automata models and

checks if these models fulﬁll speciﬁcations. The spec-

iﬁcations are expressed in temporal logic languages,

e.g. LTL (for linear time) and CTL (for branching

time). The checking is usually realized by search al-

gorithms on the modelgraphs and automata inclusion.

Like other process models EPC models provide

a more speciﬁc semantic than the automata models

of model checkers. This additional semantic is ex-

pressed by the various types of elements supported by

the EPC model: functions and events as well as orga-

nizational units and many more. These different ele-

ments have to be transformed into the automata mod-

els which serve as input for model checkers.

The problem is that our requirements speciﬁca-

tions (in temporal logic) should consider these spe-

ciﬁc model elements. Alternatively, the speciﬁcations

have to be transformed resulting in a surjective map-

ping and thus loss of information.

2 STRAIGHT FORWARD

TRANSFORMATIONS

There are different possibilities to transform EPC

models to automata which are the input to model

checkers. These automata are represented as Kripke

structures or Kripke models, respectively, which de-

ﬁne the formal framework of models in a model

checking approach. These are ﬁnite state automata in

the form of a 4-tuple consisting of a ﬁnite set of states,

a set of initial states (a subset of the set of all states), a

transition relation and a labeling function. The latter

marks states with certain properties or propositions,

respectively, which hold in the respective states.

A straight forward transformation would be just to

transform functions and states directly into automata

states. We call this a direct transformation. A sec-

ond approach is the selective transformation. This

transformation considers only some selected model

element types.

An alternative is to use a more elaborate automata

model (we call it Extended labeled Kripke Structure,

ELKS1) supporting different types of elements. We

introduce this in section 3.

We use a typical problem in e-commerce systems

in order to illustrate the functionality of these three

different concepts. The modeling of a price alert pro-

cess which checks (in a loop) all current offers as long

as there is none within a given price limit (i.e. as long

as the price threshold is not achieved). If the thresh-

old is met the system does something, in our case it

purchases.

2.1 Direct Transformation

Figure 2 depicts an EPC transformation to a format

which can be processed by current model checking

technology. Events, functions and their connection to

each other are transformed to the only means a model

checking environment provides: states and transitions

(cf. the model on the right of ﬁgure 2).

In this straight-forward mapping approach we ne-

glect the differences of the model elements and map

all notation elements to states of a Kripke structure

(for the moment we ignore the organizational unit).

We assume that the names of the events and func-

tions in the EPC model are assigned to the states as

properties by means of the labeling function within

the Kripke structure. The straight-forward mapping

PROCESS MODEL VALIDATION - Transforming Process Models to Extended Checking Models

215

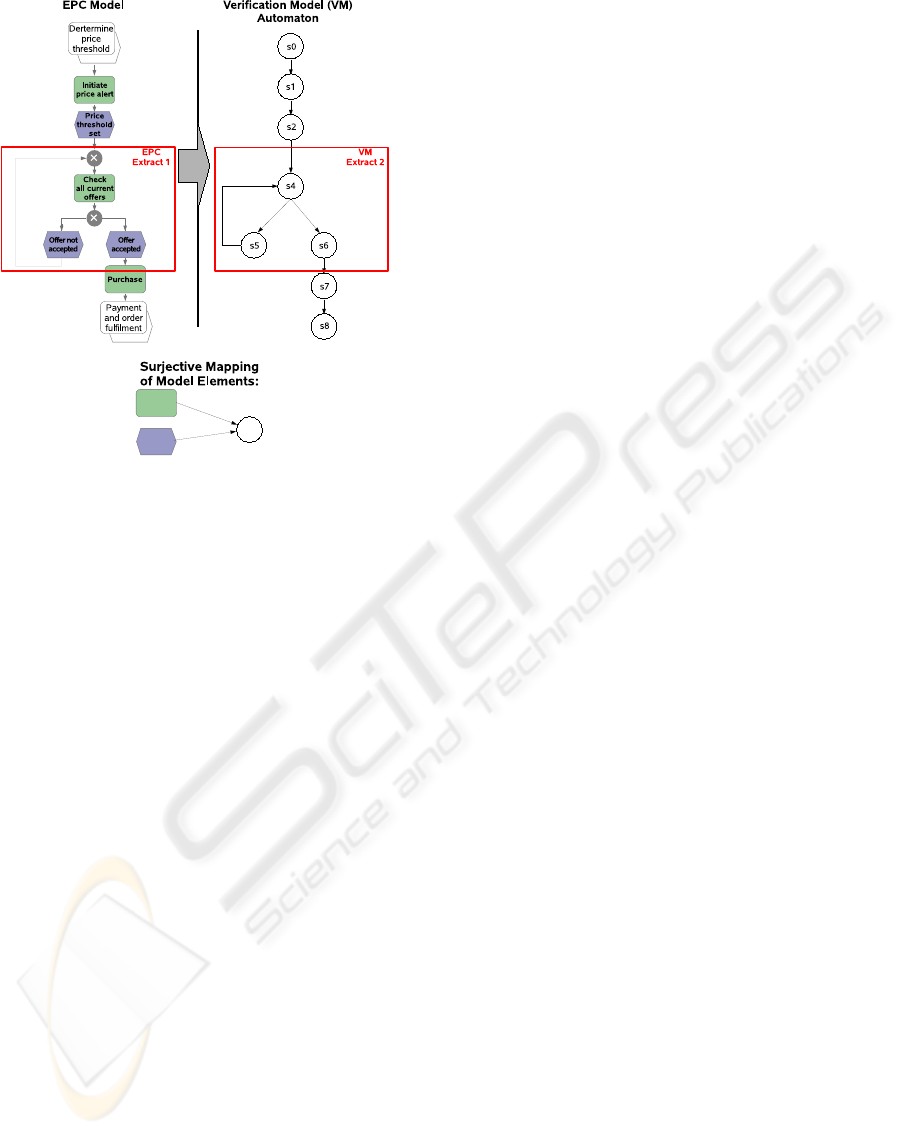
Figure 2: Example of an EPC Model.

reveals a surjective mapping. This means, in partic-

ular, that multiple elements of the domain (here the

EPC language elements for both, events and func-

tions) are mapped to one and the same element in the

co-domain (here to the notation element representing

a state). Therefore, the surjective mapping leads to a

loss of information which becomes obvious as soon

as we try to verify given requirements.

The direct transformation is easy to realize and

moreover is supported by the standard model check-

ing approaches. This means that this approach does

not require the modiﬁcation of model checking tools

and may be applied as is. The disadvantage is the

lack of detail. There is no suitable mechanism to dis-

tinguish between different element types. Hence, it

is not possible to check speciﬁc model element types

and their relations as presented in the following sec-

tion 3.

A more detailed report on this direct transforma-

tion may be found in (Speck, 2006).

2.2 Selective Transformation

The selective transformation allows skipping the

transformation of certain types of model elements.

For example only all EPC events are transformed into

the automata (ignoring all function elements). This is

comparatively coarse-grained. Nevertheless, if only a

few types of the model elements are of interest this

approach is sufﬁcient.

The resulting automata model may be processed

by an ordinary model checker or the extended check-

ing concept (as presented in the following section 3).

The latter is only reasonable if more than one model

element type should be considered.

3 EXTENDED CHECKING

CONCEPT

In this section we present the two components of

the extended checking: The transformation to an ex-

tended automata model (focusing on the model exten-

sion) and the extended algorithm for checking. This

is the third way to deal with the semantic gap as men-

tioned in section 2.

3.1 Extended Checking Model

In an extended Kripke structure we separate different

types of model elements (Pulverm¨uller, 2009). In our

case these are events and functions (c.f. ﬁgure 3). By

means of transition states (event states) the transitions

become ﬁrst-order objects. This approach is similar

to association classes in UML. Transition states play a

double role: On the one hand theyrepresent the transi-

tion in the traditional way and, on the other hand, the

transition state is treated equally to traditional states

in a model checking approach. This has an impact

on the properties which may be assigned to transition

states, as well. Furthermore, upgrading a transition

to a ﬁrst-order object opens enhanced possibilities to

their veriﬁcation. In ﬁgure 3 the transition states are

depicted with rectangles.

The distinction of different kinds of elements in

the automata (and the Kripke structures) is the base

of improved checking algorithms. These algorithms

are able to distinguish between the different types of

elements and to support a more detailed speciﬁcation

as described in the following subsection.

The transformation to an extended model requires

a more elaborated transformation mechanism. The

ordinary Kripke structure has to be modiﬁed as de-

scribed in (Pulverm¨uller, 2009). However, now we

may formulate speciﬁcations which are not supported

within the direct transformation. We illustrate this

problem by checking the models in ﬁgures 2 and 3

by the following sample CTL speciﬁcation:

Always

Check all current offers

Until

Offer accepted

With the direct transformation we cannot distinguish

between different model elements (

functions

and

events

). Hence, the checker would present an error.

We propose to use the specializer operators

Function

and

Event

which means that we distinguish between

the model elements within our speciﬁcation and also

within the extended model checking algorithm. With

ENASE 2010 - International Conference on Evaluation of Novel Approaches to Software Engineering

216

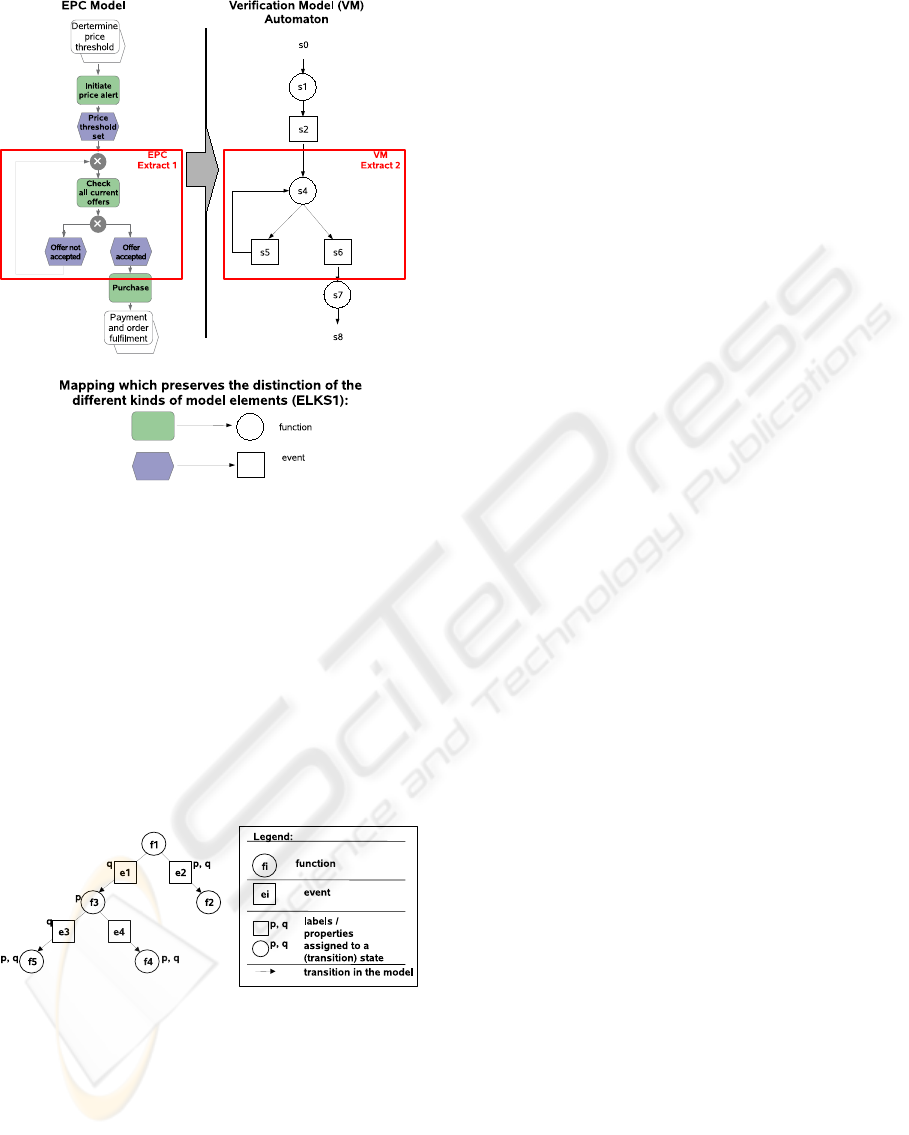
Figure 3: EPC Transformation to Extended Automaton.

our extended speciﬁcation the above mentioned ex-

ample requirement looks as follows: Always (Func-

tion [

Check all current offers

] Until Event [

Offer ac-

cepted

]). It means: We check that the function

Check

all current offers

is true and do not consider other

events unless the event

Offer accepted

(and no other

function) becomestrue. This speciﬁcation using func-

tions and events specializers is true which we expect

as result. We want to be able to select speciﬁc el-

ement types and focus on these in the speciﬁcation.

This is an extension of the temporal logic CTL we

call ECTL1 (Extended CTL).

Figure 4: EPC Transformation to Extended Automaton.

3.2 Checking ECTL1 Models

Our extended speciﬁcation and model checking is

based on CTL (model checking). With our exten-

sion we can specify more semantic information over

a semantically extended veriﬁcation model thus be-

ing more ﬁne-grained and more precise in our require-

ments.

Figure 4 depicts an abstract example for an

ELKS1 (an extended Kripke structure). We ignore

the requirement of a total relation to simplify the ex-

ample. In the example model the propositions p and

q hold in s4, for instance. The events in the result set

fulﬁll the given ECTL1 formula if chosen as starting

state. The ﬁrst of the examples below means: If s is

one of the states in the set R and if s is taken as the

starting state in the system model M then the prop-

erty (or requirement, respectively) p is fulﬁlled in the

model (M, s |= p).

ECTL1 examples (based on CTL):

(1.) M, s |= p, result set R: s ∈ R = { e2, f3, f4, f 5 }

(2.) M, s |= Function[p], result set R: s ∈ R = { f3, f4, f 5 }

(3.) M, s |= Event[ p], result set R: s ∈ R = { e2 }

(4.) M, s |= p∧ q, result set R: s ∈ R = { e2, f 4, f5 }

(5.) M, s |= Function[p] ∧ Function[q], result set R: s ∈ R = { f4, f5 }

(6.) M, s |= Function[p] ∧ Event[q], result set R: s ∈ R = { }

(7.) M, s |= Event[ p] ∨ Event[q], result set R: s ∈ R = { e1, e2, e3 }

(8.) M, s |= EX p, result set R: s ∈ R = { f 1, e1, f3, e3, e4 }

(9.) M, s |= AX Function[ p], result set R: s ∈ R = { e1, f 3, e3, e4 }

(10.) M, s |= Function[AX Function[p]], result set R: s ∈ R = { f3 }

(11.) M, s |= E[p U q], result set R: s ∈ R = { e1, e2, f 3, e3, f4, f5 }

(12.) M, s |= Function[E[pU q]], result set R: s ∈ R = { f 3, f4, f5 }

(13.) M, s |= E[Function[p] U Function[q]], result set R: s ∈ R = { e1, f3, e3, e4, f4, f 5 }

(14.) M, s |= E[Event[q] U Function[p]], result set R: s ∈ R = { f 1, e1, f 3, e3, f 4, f5 }

(15.) M, s |= A[Event[p] U Function[ p]], result set R: s ∈ R = { f4, f5 }

(16.) M, s |= A[Event[q] U Function[p]], result set R: s ∈ R = { e3, f 4, f5 }

(17.) M, s |= AF p, result set R: s ∈ R = { f 1, e1, e2, f 3, e3, e4, f 4, f5 }

The example point to some special aspects. The

following explanations refer to the example numbers

given above.

The formulas in (1.) and (4.) are trivial and not

very different to traditional CTL. Examples (2.) and

(3.) demonstrate the specializers in their work as ﬁl-

ters over the result set of example (1.).

In (8.), for instance, state f3 (which is a function

state) is in the result set although it does not fulﬁll

EX p in the traditional CTL logic. In ECTL1, how-

ever, we consider half-steps. In a next step f3 reaches

a function state (here even two, f5 and f4) in which

p holds. Due to these function states f5 and f4, both,

the function state f3 as well as the event states e3 and

e4 are in the result set.

State f1 is not contained in the result set of (9.)

since there is a path ( f1, e2, f2) on which the next

function state does not fulﬁll Function[p]. In other

words, AX Function[p] does not hold in f1 due to

the fact that p does not hold in f2. This is different

for the formula EX Function[p] as only one path is

needed. This is fulﬁlled by the path (f1, e2, f3, . . . ).

As opposed to Function[AX p] the result set in (9.)

also contains function states. In (10.) we ﬁlter the

result set of (9.) eliminating all function states.

PROCESS MODEL VALIDATION - Transforming Process Models to Extended Checking Models

217

Example (11.) to (16.) give several variants of the

Until-operator with focus on the effect of the addi-

tional specializers. While example 11. may be trans-

lated to CTL by mapping function states and event

states to states (loosing the distinction between the

two) this is not generally the case for the successive

examples. Example (12.) ﬁlters the outcome of (11.)

and just eliminates all event states from the result set.

As opposed to that, the variant in example (13.) con-

tains both, function states and event states. Example

(13.) starts in all function states in which q holds and

walks backwards until a function state is reached in

which p holds. The event states are just collected and

inserted in the result set if they are on the path. There

is no evaluation performed on them. Even event state

e1 is in the result set although neither the formula

Function[p] nor Function[p] nor p hold in it. Event

state e1 is only in the result set due to f3. The result

set is maximized and therefore, we traverse the graph

backwards until we reach a function state in which the

formula does not hold. On our way back from f3 we

just collect e1 and do not evaluate any formula in it.

This is different for example (14.). Function state f4

is in the result set as it directly fulﬁlls Function[p].

Still we do not collect e4 into the result set on our

way backwards through the graph because the ﬁrst

part of the formula Event[q] enforces an evaluation

on event states. However, Event[q] or q, respectively,

does not hold in e4. On the other hand, f1 is in the re-

sult set which is due to the fact that it is just collected

(as it was the case for e1 in example (13.)). Event[p]

does not apply to function states and as the result set

is maximized f1 is inserted into it. Due to the fact

that there might start a branch in a function state (as

it is true for f1) we have to take care for the Always-

quantiﬁer. If we substitute E by A in example (14.)

function state f1 is eliminated from the result set due

to the second branch. The second branch ( f1, e2, f2)

has (in the given excerpt) no function state in which

Function[p] or p, respectively, holds. As in CTL

we could insert a Weak Until-operator (WU). As

opposed to A[Event[q] U Function[p]] the formula

A[Event[q] WU Function[p]] would contain f1 in the

result set due to Event[q] in event state e2. Proposi-

tion q holds inﬁnitely in all event states on the path

starting in f1. In our example ECTL1 model this is

only the case because we limit to an excerpt and ig-

nored that real models have to be total (i.e. in a real

model f2 would have at least one successor which

could change all our statements of the previous sen-

tences).

Example (16.) demonstrates again the difference

of the Always-operator. While f 3 is in the result set

of example (14.) this is not the case in example (16.)

because starting in f3 there is only one path on which

q holds in all event states until a function state is

reached in which p holds.

4 RELATED WORK

Our approach is based on the model checking technol-

ogy (Grumberg and Veith, 2008; Clarke et al., 2001b)

which itself is already a push-button veriﬁcation ap-

proach. This allows automating many steps releasing

the developer and end-user of tedious mathematical

tasks. In model checking the veriﬁcation of process

models and software has always been a research issue.

Already early approaches like (Emerson and Clarke,

1980) or (McMillan, 1993) are about the veriﬁcation

of models. However, all approaches imply a gap be-

tween the models and the checked automata.

A new alternative path to decrease the gap to ver-

iﬁcation models is to provide veriﬁcation environ-

ments making the veriﬁcation or compliance check-

ing more convenient (El Kharbili and Pulverm¨uller,

2009). Tools to simulate and generate or export veri-

ﬁcation models ease the task of a developer. This of-

ten embraces an automatic transformation of higher-

level models to a model format the checker under-

stands (F¨otsch et al., 2005). Though this closes some

gap between the user and the veriﬁcation level it does

not consider the information loss which comes with

the (automatic) mapping to the low-level veriﬁcation

models.

In logics there are further approaches to improve

this semantic expressiveness (however, often without

clear relation to software development models and

their different kinds of model elements). Such ap-

proaches may be found in the µ-calculus (Bradﬁeld

and Stirling, 2001; Kozen, 1983) or the multi-valued

logic research, e.g. (Chechik et al., 2003). In the lat-

ter, the logic is extended from the Boolean TRUE and

FALSE to further values (e.g. DON

′

T KNOW in a

three-valued logic). Extensions to the temporal logic

for LTL have been proposed in (Sagar Chaki et al.,

2004) or (Jonsson et al., 1990) and in (De Nicola

et al., 1993; De Nicola and Vaandrager, 1990). How-

ever, a link to software development models is miss-

ing as well as the general idea of specializers for dif-

ferent model elements. As opposed to (Sagar Chaki

et al., 2004; Jonsson et al., 1990; Giannakopoulou

and Magee, 2003; Kindler and Vesper, 1998) we

are able to explicitly distinguish and mix specializers

(and thus views) for different model elements.

ENASE 2010 - International Conference on Evaluation of Novel Approaches to Software Engineering

218

5 CONCLUSIONS

The paper presents three approachesfor checking pro-

cess or workﬂow models.

The initial problem is the gap between the process

or workﬂow models with their various model element

types on the one hand and on the other hand the au-

tomata models serving as input for model checkers.

The ﬁrst approach is a direct transformation map-

ping multiple model element types to one single ver-

iﬁcation model element type (surjective mapping).

The second approach supports the selection of spe-

ciﬁc model element types and transforms these while

ignoring the others. The extended model checking

approach results in the least loss of semantic infor-

mation. It extends the speciﬁcation language as well

as the veriﬁcation modeling language. It introduces

specializers, e.g.

Function

and

Event

for EPC check-

ing. In this way it enables a more precise require-

ments speciﬁcation.

A further improvement may be the support by a

graphical representation of the model and the speciﬁ-

cation to ease the use for domain experts.

REFERENCES

B´erard, B., Bidoit, M., Finkel, A., Laroussinie, F., Petit, A.,

Petrucci, L., and Schnoebelen, P. (2001). Systems and

Software Veriﬁcation – Model-Checking Techniques

and Tools. Springer, Berlin, Germany.

Bradﬁeld, J. and Stirling, C. (2001). Modal logics and mu-

calculi: an introduction. In Bergstra, J. A., Ponse,

A., and Smolka, S. A., editors, Handbook of Process

Algebra, pages 293–330. Elsevier Science Publishers

B.V., Amsterdam, The Netherlands.

Breitling, M. (2002). Business Consulting, Service Pack-

ages & Beneﬁts. Technical report, Intershop Customer

Services, Jena, Germany.

Chechik, M., Devereux, B., Easterbrook, S., and Gurﬁnkel,

A. (2003). Multi-Valued Symbolic Model-Checking.

ACM Transactions on Software Engineering Method-

ology, 12(4):371–408.

Clarke, E. M., Grumberg, O., and Peled, D. A. (2001a).

Model Checking. The MIT Press, Cambridge, Mas-

sachusetts; London, England, 3 edition.

Clarke, E. M., Grumberg, O., and Peled, D. A. (2001b).

Model Checking. The MIT Press, Cambridge, Mas-

sachusetts; London, England, 3 edition.

De Nicola, R., Fantechi, A., Gnesi, S., and Ristori, G.

(1993). An action based framework for verifying log-

ical and behavioural properties of concurrent systems.

Computer Networks and ISDN Systems, 25(7):761–

778.

De Nicola, R. and Vaandrager, F. (1990). Action versus

state based logics for transition systems. In Guessar-

ian, I., editor, Proceedings of the LITP Spring School

on Theoretical Computer Science on Semantics of Sys-

tems of Concurrent Processes, volume 469 of Lecture

Notes in Computer Science, pages 407–419. Springer-

Verlag New York, Inc.

El Kharbili, M. and Pulverm¨uller, E. (2009). A Semantic

Framework for Compliance Management in Business

Process Management. In Proceedings of the 2nd Inter-

national Conference on Business Process and Service

Computing (BPSC’09) as Part of Software, Agents

and Services for Business, Research, and E-Sciences

(SABRE), pages 60–80.

Emerson, E. A. and Clarke, E. M. (1980). Characteriz-

ing Correctness Properties of Parallel Programs Us-

ing Fixpoints. In ICALP 1980, Automata, Languages

and Programming, 7th Colloquium, pages 169–181.

Springer LNCS 85.

F¨otsch, D., Speck, A., Rossak, W., and Krumbiegel, J.

(2005). A Concept of Modelling and Validation of

Web based Presentation Templates. In 17. Interna-

tionale Tagung Wirtschaftsinformatik 2005 (WI2005),

pages 391–406. Physika Verlag.

Giannakopoulou, D. and Magee, J. (2003). Fluent Model

Checking for Event-based Systems. In Proceedings

of the 9th European Software Engineering Conference

(ESEC) held jointly with 10th ACM SIGSOFT Inter-

national Symposium on Foundations of Software En-

gineering (FSE), pages 257–266. ACM Press.

Grumberg, O. and Veith, H., editors (2008). 25 Years of

Model Checking - History, Achievements, Perspec-

tives, volume 5000 of Lecture Notes in Computer Sci-

ence. Springer.

Jonsson, B., Khan, A. H., and Parrow, J. (1990). Implement-

ing a Model Checking Algorithm by Adapting Exist-

ing Automated Tools. In Sifakis, J., editor, Proceed-

ings of the International Workshop on Automatic Veri-

ﬁcation Methods for Finite State Systems, volume 407

of Lecture Notes in Computer Science, pages 179–

188, New York, USA. Springer-Verlag.

Kindler, E. and Vesper, T. (1998). ESTL: A Temporal Logic

for Events and States. In Proceedings of the 19th In-

ternational Conference on Application and Theory of

Petri Nets (ICATPN), pages 365–384. Springer LNCS

1420.

Kozen, D. (1983). Results on the propositional mu-calculus.

Theoretical Computer Science, 27(3):333–354.

McMillan, K. L. (1993). Symbolic Model Checking. Kluwer

Academic Publishers.

OMG (2006). Business process modeling notation (bpmn)

speciﬁcation. Technical report, Object Management

Group (OMG). http://www.omg.org/docs/dtc/06-02-

01.pdf.

Pulverm¨uller, E. (2009). Reducing the Gap between Ver-

iﬁcation Models and Software Development Mod-

els. In The 8th International Conference on Software

Methodologies, Tools and Techniques (SoMeT 2009),

pages 297–313. IOS Press.

Sagar Chaki, S., M., C. E., Ouaknine, J., Sharygina, N.,

and Sinha, N. (2004). State/Event-Based Software

PROCESS MODEL VALIDATION - Transforming Process Models to Extended Checking Models

219

Model Checking. In Proceedings of the 4th Inter-

national Conference on Integrated Formal Methods

(IFM), volume 2999 of Lecture Notes in Computer

Science, pages 128–147. Springer-Verlag.

Scheer, A.-W. (1998). ARIS - Modellierungsmethoden,

Metamodelle, Awendungen. Springer, Berlin, Ger-

many.

Scheer, A.-W. and N¨uttgens, M., editors (2000). ARIS Ar-

chitecture and Reference Models for Business Process

Management., volume 1806 of Lecture Notes in Com-

puter Science. Springer.

Speck, A. (2006). Modelling and Verifying of e-Commerce

Systems. In Proceedings of International Work-

shop on Regulations Modelling and their Validation

and Veriﬁcation (REMO2V’06) in conjunction with

CAiSE’06, pages 857–863.

ENASE 2010 - International Conference on Evaluation of Novel Approaches to Software Engineering

220