
Using Model Transformation to Facilitate Dynamic
Context Adaptation
Sylvain Degrandsart
12
, Serge Demeyer
1
and Tom Mens
2
1
Department of Mathematics and Computer Science, Universiteit Antwerpen
Universiteitsplein 1, B-2610 Antwerpen, Belgium
2
University of Mons – UMONS, Place du Parc 20, 7000 Mons, Belgium
Abstract. The widespread adoption of mobile computing opens the path for
more user-centric applications, that need to be continuously and dynamically
adapted to different contexts of use. Dealing with such dynamic context adap-
tation requires a significant amount of effort, due to the high number of con-
texts that need to be dealt with, as well as the widespread impact that a context
change may have. In this article, we propose a change-based approach to context
adaptation that reduces the effort and redundancy of dynamic context adaptation
through the use of semi-automated and formally specified model transformations.
We provide a proof-of-concept using graph transformation, and show how trans-
formation analysis helps to explore the space of reachable contexts.
1 Introduction
A context-sensitive software system is a software system that should adapt gracefully
to different contexts of use. A well-known example is the mobile museum guide that
displays general information about the current exposition, as well as detailed informa-
tion about a particular piece of art depending on the distance between the visitor and
this piece of art [1]. Moreover, the mobile guide adapts to its context by dynamically
modifying the type of user interface in function of the type of visitor.
Dynamic context adaptation is difficult to manage in traditional, code-centric, soft-
ware development, as the notion of context varies a lot from system to system [2]. In
addition, there are many different ways in which a system should be able to adapt to
different contexts of use. These problems can be address using a model-driven software
development. Models enable us to define appropriate abstractions to isolate and specify
the different contexts of use.
Several attempts have been made in research literature to use model-driven ap-
proaches for specifying context-sensitive applications [3, 4]. They all have in common
that they provide different models of the application for every possible context of use,
the context-specific models. This leads to several scalability issues related to the num-
ber of contexts that increases rapidly due to the combinatorial explosion of context
variables and their possible values. First, the number of context-sensitive models di-
rectly follows the number of contexts, leading to a high redundancy in the specification.
A second scalability problem is related to context adaptations. In order to explore and
Degrandsart S., Demeyer S. and Mens T.
Using Model Transformation to Facilitate Dynamic Context Adaptation.
DOI: 10.5220/0003016900070019
In Proceedings of the 2nd International Workshop on Future Trends of Model-Driven Development (ICEIS 2010), page
ISBN: 978-989-8425-10-2
Copyright
c
2010 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

specify how to change from one context to another, potentially all possible pairs of
contexts need to be considered.
Because of the aforementioned problems, alternative solutions need to be consid-
ered. We propose to solve the scalability issues by adopting a model transformation
point of view. Model transformations allow us to specify context adaptations at an ap-
propriate level of abstraction. Taking the analogy with versioning approaches [5], one
could say that we propose to explore a change-based (or delta-based) approach as op-
posed to a state-based approach. Instead of specifying a model of the entire application
for every possible context of use, we propose a novel approach in which the application
is entirely modeled only once according to an initial context. Model transformations
specifying precisely how to adapt a context-specific model to obtain the model corre-
sponding to another context, are grafted to this model to form a specification of the
context-sensitive application. Such an explicit representation of context changes allows
us to remove redundancy as the context-specific models can be generated automatically
from these model transformations.
A theoretical approach towards model transformation enables reasoning about for-
mal properties of dynamic context adaptation. For example, it enables us to determine
the space of contexts covered by a specification (i.e., context coverage), as well as the
set of dynamic adaptations covered by a specification (i.e., context change coverage).
This information can be used to determine whether a given set of model transformations
is sufficient to cover the required set of contexts. It can also guide the developer in spec-
ifying additional model transformations if this would be needed in order to reach more
context-specific models. As a proof-of-concept illustrating these ideas, we carry out a
small case study using graph transformation theory, implemented in the AGG tool [6].
The remainder of this article is structured as follows. We start by a study of related
work in section 2. We continue by motivating our work through a running example
introduced in section 3. Section 4 presents our change-based model for dynamic context
adaptation. In section 5 we perform a feasibility study using the graph transformation
formalism. Finally, we discuss the advantages, shortcomings and future work of our
approach in section 6.
2 Related Work
Since the widespread adoption of mobile computing devices integrating context sen-
sors (such as light sensors, global positioning systems, pressure sensors, . . . ) there is
an increasing interest for context-sensitive applications that use these data sources to
enhance the user experience.
The majority of the attempts to handle the complexity introduced by the notion of
context have been focusing on models of the human-computer interaction domain [3, 4].
For example, Souchon et al. [7] describe how multi-context task models can be used to
represent context-sensitive application user interfaces. Such a multi-context task model
is composed of a collection of context-specific task models describing the interaction
between the application and the user in a particular context. To avoid redundancy, the
commonalities between the context-specific task models are factored out into a context-
independent task model. But as the number of context increase, the number of common-
8

alities between all the context-specific models will drastically decrease, concluding to
scalability suffering state-based model.
Another example is CUP 2.0 [8], a UML profile
3
for high-level modeling of context-
sensitive interactive applications. It was mainly created to ease the communication be-
tween human-computer interaction specialists and software designers, but it can also
be used for semi-automatic generation of low fidelity user interface prototypes. The
UML profile supports five different kinds of model: application model, context model,
system interaction model, abstract user interface model and user interface deployment
model. This profile has been developed to specify a context-specific model and so has
no mechanism to deal with the scalability problem we are facing.
With our change-based approach, we go beyond the human-computer interaction
domain, its specific modeling languages and its specific goals. We concentrate our ef-
fort on the model-driven engineering process necessary to support dynamic context
adaptation when the number of considered context increase.
3 Running Example
As a running example to illustrate our ideas, we present a fictitious context-sensitive
application called ‘Mobilessence’. It is designed to run on a mobile computing device
such as a smartphone, equipped with a GPS. The default functionality is very simple: the
application only displays the current time. The display interface is dynamically adapted
according to user preferences and space available on the small-sized screen. For this
specific application, context is specified using two variables: the owner of the mobile
phone on which Mobilessence runs (i.e., user-specific preferences); and the means of
transportation with two possible values: car and hand. The former indicates that the
device is being used in a car (i.e., connected to its docking station), the latter indicates
that the device is hand-carried by its owner. The object structure of Mobilessence is
specified in the class diagram of Figure 1. The System uses a Frame to display the time
via a Clock, that is characterised by a size and a colour. Clock is an abstract class that
is specialised into AnalogClock and DigitalClock. A Frame has a size, that is relative
to the computing device’s screen size, a background colour (bgColour) and a closable
boolean value. The Frame can use as background an Image that has a target location on
the device memory and an encoding type. Finally, a GPS function can be displayed in a
Frame. The GPS also requires to specify a destination address and the required screen
size.
In our current example, three different (types of) owners will use the application:
Alice, Bob and Charlie. Alice being a ‘The Matrix’ movie fan, she likes green
and black colours and would therefore like Mobilessence to display a green clock on a
black background. Whenever she takes her mobile phone out of her bag, she typically
only wants to see the time, so the clock display will use up all screen estate to facili-
tate reading the time. The context-specific model M
(alice,hand)
of Figure 2 (which is
an object diagram that is an instance of the class diagram of Figure 1) shows the spec-
ification of Mobilessence for that particular context. When Alice plugs her mobile
3
UML is a standardised general-purpose modeling language created and maintained by the
Object Management Group http://www.uml.org/
9
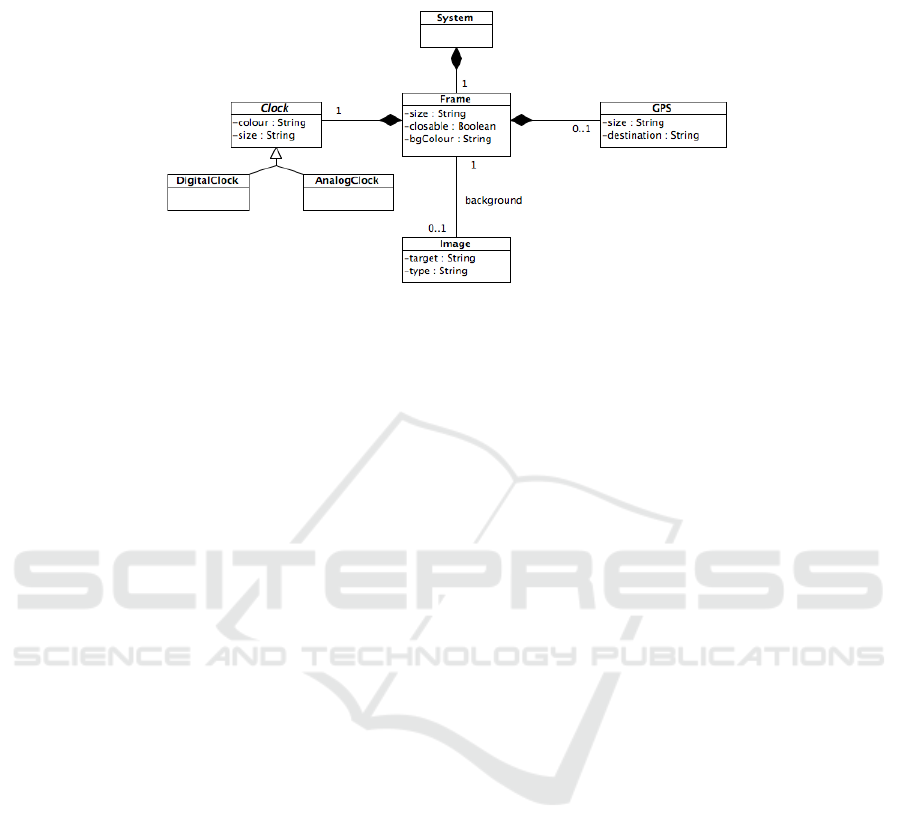
Fig. 1. Mobilessence class diagram.
phone in her car, she needs the GPS function but is still interested by the time as well.
The context-specific model M
(alice,car )
of Figure 2 therefore requires the application
to use a different display interface in that particular context: the time is displayed using
a digital clock (in order to reduce its size), and the GPS function occupies the rest of
the screen.
Bob prefers to have his mobile device display a picture of his wife on the back-
ground, and he wants the clock hands to be displayed in black on top of this picture.
Context-specific model M
(bob,hand)
of Figure 2 specifies the application interface and
properties when Bob carries his mobile phone in his hand or pocket. When he is in
his car, as was the case for Alice, the GPS function requires space on the frame to
be displayed, so a digital clock is used to gain space. Bob’s wife’s picture remains on
the background of the clock display as he prefers it. The specification of this context-
specific model M
(bob,car)
is given in Figure 2.
Charlie, our third user, has visual disabilities, which makes it difficult for him to
distinguish the hands of an analog clock. He therefore prefers to display a black digital
clock on a white display to enhance readability when taking his mobile phone out of
his pocket. Context-specific model M
(charlie,hand)
of Figure 2 reflects that situation.
When Charlie is in his car, GPS information and time are both displayed, following
context-specific model M
(charlie,car)
of Figure 2.
As we can see from Figure 2, this context-sensitive specification for Mobilessence
is composed of six models, one for each supported context of use. It is clear that the
differences between all of these context-specific models are relatively small compared
to the size of the models. This will become more apparent for bigger models, where
the size of the context change will represent only a fraction of the size of the context-
specific model being dynamically adapted.
Our approach aims to remove unnecessary redundancy by specifying only the chan-
ges between context-specific models. In other words, we propose to represent only the
modifications needed to dynamically adapt to a different context. For example, if Bob
plugs his mobile device in his car, the dynamic context adaptation is composed of two
operations: the device needs to switch from an analog to a digital clock display; and
we have to add the GPS function into the frame. Most of the other properties, such as
10
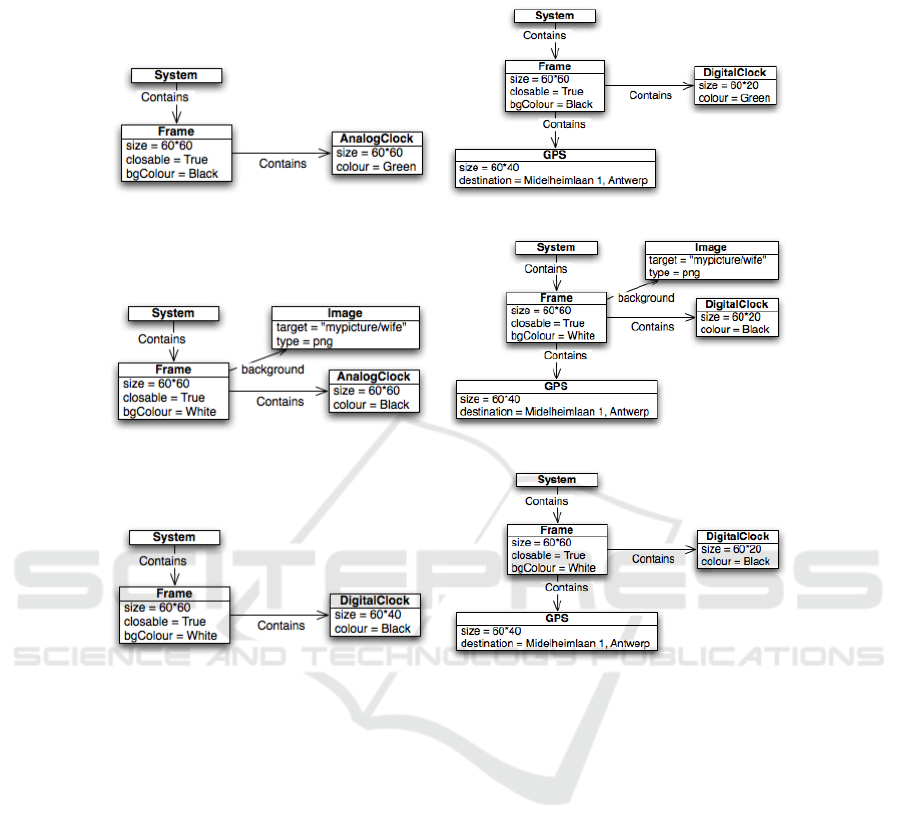
M
(alice,hand)
M
(alice,car)
M
(bob,hand)
M
(bob,car)
M
(charlie,hand)
M
(charlie,car)
Fig. 2. Context-specific object models for the six possible contexts of the Mobilessence applica-
tion.
colour, frame size and background image are not modified during the context change
from hand to car.
4 A Change-based Approach for Dynamic Context Adaptation
A context-sensitive application is a software application whose functionality can be
dynamically adapted depending on the context in which it is used. To formalise these
notions, let us introduce the following definitions:
Definition 1 (Context and Context Domain). A context-sensitive application can
have a finite number n ∈ N of variabilities. For all i ∈ 1 . . . n, each variability is
11

defined by a finite set V
i
that represents all possible variations.
4
The context domain is
defined by C = V
1
× V
2
× . . . × V
n
. A context c = (v
1
, v
2
, . . . v
n
) ∈ C is thus a tuple
composed of n values, one for each variability V
i
.
For our simple running example, there are two variabilities Ow ner = {alice, bob,
charlie} and T ransportation = {hand, car }, so the context domain is C = Owner×
T ransportation. This defines six possible contexts (alice, hand), (alice, car), (bob,
hand), (bob, car), (charlie, hand) and (charlie, car).
Given a particular context c ∈ C, we denote a context-specific model (i.e., a model
belonging to this context) as M
c
. Typically, such a context-specific model will be com-
posed of a variety of different diagrams. For example, if we use UML as modeling
language, a model could be specified as a combination of object diagrams, sequence di-
agrams, state machine diagrams, use case diagrams and many more. For reasons of clar-
ity and compactness, however, our running example only uses object diagrams. They
are shown in Figure 2 for each of the six possible contexts.
Definition 2 (Context Change). A context change is a pair (c, d) ∈ C × C.
Given a context-specific model M
c
belonging to context c, the impact of the context
change (c, d) on the model can be described by a model transformation T
c,d
. Applying
this model transformation to M
c
will result in a context-specific model M
d
belonging
to context d. In our running example, given the context-specific model M
(alice,hand)
,
the model transformation for the context change ((alice, hand), (alice, car)) can be
expressed formally by the model transformation T
3
of Figure 3.
5
Similarly, the context
change ((alice, hand), (bob, hand)) can be described by the model transformation T
1
of Figure 3.
Let us now define the context coverage as the set of all possible contexts of C reach-
able from an initial context-specific model. We distinguish between a weak and a strong
(symmetrical) notion of context coverage:
Definition 3 (Context Coverage). Let T = {T
1
, . . . , T
m
} be a finite set of model
transformations, c ∈ C an initial context, and M
c
a context-specific model belonging to
context c.
weakCoverage
C
(c, M
c
, T ) = {d ∈ C | ∃ model transformation sequence S of model
transformations ∈ T
such that applying S to M
c
results in a model M
d
belonging to context d }
coverage
C
(c, M
c
, T ) = {d ∈ weakCoverage
C
(c, M
c
, T ) | ∃M
d
belonging to d such
that c ∈ weakCoverage
C
(d, M
d
, T )}
Based on these two notions of context coverage we can define, for each of them, the
corresponding notion of context-change coverage as the set of context changes gener-
ated by a context coverage.
4
We assume in our approach that variabilities are discrete, as we are not aware of any related
work that requires to deal with an infinite number of contexts.
5
See section 5 for a more detailed explanation of the formalism used to specify model transfor-
mations.
12

Definition 4 (Change Coverage). weakChangeCoverage
C
(c, M, T ) = {(c
1
, c
2
) ∈
C × C | c
1
, c
2
∈ weakCoverage
C
(c, M, T )
and c
2
∈ weakCoverage
C
(c
1
, M
1
, T ), with M
1
a context-specific model belong-
ing to context c
1
}
changeCoverage
C
(c, M, T ) = {(c
1
, c
2
) ∈ C × C | c
1
, c
2
∈ coverage
C
(c, M, T )
and c
2
∈ coverage
C
(c
1
, M
1
, T ), with M
1
a context-specific model belonging to
context c
1
}
Property 1.
weakChangeCoverage
C
(c, M, T ) is a transitive relation over context domain C.
changeCoverage
C
(c, M, T ) is a symmetric and transitive relation over context domain
C.
The notion of context change coverage is very useful to reason about the set of pos-
sible context changes that are applicable from an initial context-specific model, as well
as the set of context-specific models that are reachable from the initial model. Visu-
ally, the change coverage relation can be represented as a graph. Analysing this graph
allows us to determine easily which contexts are not reachable from the initial context-
specific model using the set of transformations T . Such analysis is very useful, as it
allows us to verify whether the design of a context-sensitive application conforms to
its specification. By adding more transformations to the set T , we can make more con-
texts reachable from the initial context-specific model. Another advantage of the change
coverage relation is that it facilitates reasoning about the formal properties of the trans-
formations belonging to T (such as critical pair analysis, applicability, reversibility, and
so on), and exploit these properties to reduce the effort of developing context-sensitive
applications. We explain how this can be done in the next section, after having shown
how model transformations can be specified formally using the notion of graph trans-
formation.
Let us conclude this section with one final remark. The notion of context change
coverage is not only useful to analyse context changes. Another crucial feature is its
ability to generate context-specific models for each context that is reachable from the
initial context (by applying sequences of model transformations belonging to T ). It
is exactly this feature that allows us to remove redundancy in the specification of a
context-sensitive application, as this relieves us from the need to store all context-
specific models explicitly.
5 Feasibility Study
As a proof of concept, we show how our change-based approach can be used to specify
context-sensitive applications, and how context change coverage can be used to explore
the space of contexts supported by such a specification. We will use the Attributed
Graph Grammar system (AGG) [6]. Models and model transformations can be for-
mally specified in AGG by graphs and graph transformations, respectively. Moreover,
AGG offers the possibility to apply transformations and to verify several formal proper-
ties (e.g. syntactical well-formedness, type conformance, transformation applicability,
13
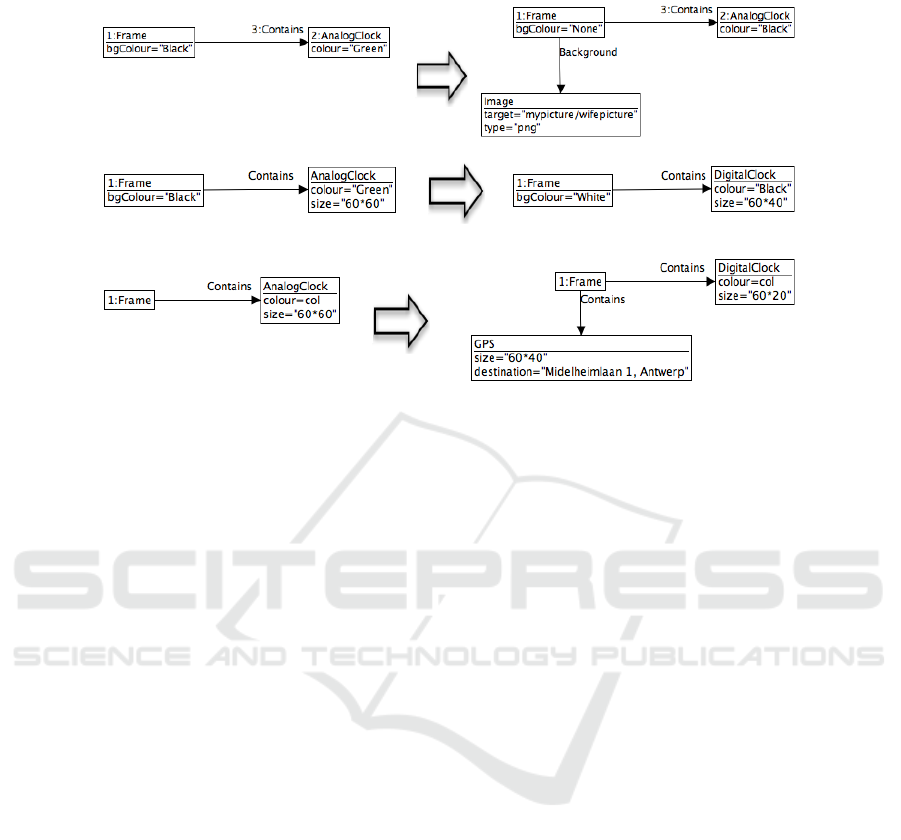
T
1
T
2
T
3
Fig. 3. Mobilessence’s set of model transformations T = {T
1
, T
2
, T
3
}.
critical pair analysis). In this section, we revisit the running example Mobilessence in-
troduced in section 3 to illustrate the concepts defined in section 4.
As initial context we will use (alice, hand). The corresponding initial context-
specific model M
(alice,hand)
is represented as a typed, attributed, directed graph in
Figure 2. In other words, the model is represented as a set of typed nodes, connected by
typed directed edges, and the nodes may contain multiple attribute values.
The model transformations of T are expressed as graph transformations. In our
running example, the set T contains three graph transformations, displayed in Figure 3.
T
1
describes the transformation for the ((alice, hand), (bob, hand)) context change,
T
2
describes the ((alice, hand), (charlie, hand)) context change and T
3
describes the
((alice, hand), (alice, car)) context change.
Each graph transformation is composed of a left-hand-side and a right-hand-side.
The former represents a subgraph that needs to be matched in the host graph we want
to transform. The latter describes how this subgraph will be replaced by a different sub-
graph (for the given match in the host graph). Elements belonging to the left-hand-side
that are absent from the right-hand-side are deleted by the transformation, elements of
the right-hand-side that are absent from the left-hand-side are created by the transfor-
mation, and node attributes with a differing left and right value will be modified by the
transformation.
For instance, graph transformation T
1
of Figure 3 can be used to specify the context
change ((alice, hand), (bob, hand)). By applying this graph transformation to graph
M
(alice,hand)
, the initial context-specific model will be modified as follows. Firstly, the
value of background colour attribute bgColour of Frame is modified from “Black” to
“None”. Secondly, the value of the colour attribute of AnalogClock is modified from
“Green” to “Black”. Thirdly, an Image node is created with two corresponding values
for its attributes target and type. Finally, a Background edge is created between the
14

Frame node and the Image node. The final result of this graph transformation applica-
tion will be the context-specific model M
(bob,hand)
of Figure 2.
Given c = (alice, hand) as initial context with corresponding initial context model
M
c
. If we compute the weak coverage using our set of three model transformations,
then we obtain the following results:
weakCoverage(c, M
c
, T ) = {(alice, hand), (alice, car), (bob, hand), (bob, car ),
(charlie, hand)}
weakChangeCoverage(c, M
c
, T ) =
{((alice, hand ), (alice, car)), ((alice, hand), (bob, hand)), ((alice, hand),
(charlie, hand)), ((bob, hand), (bob, car )), ((alice, hand), (bob, car))}
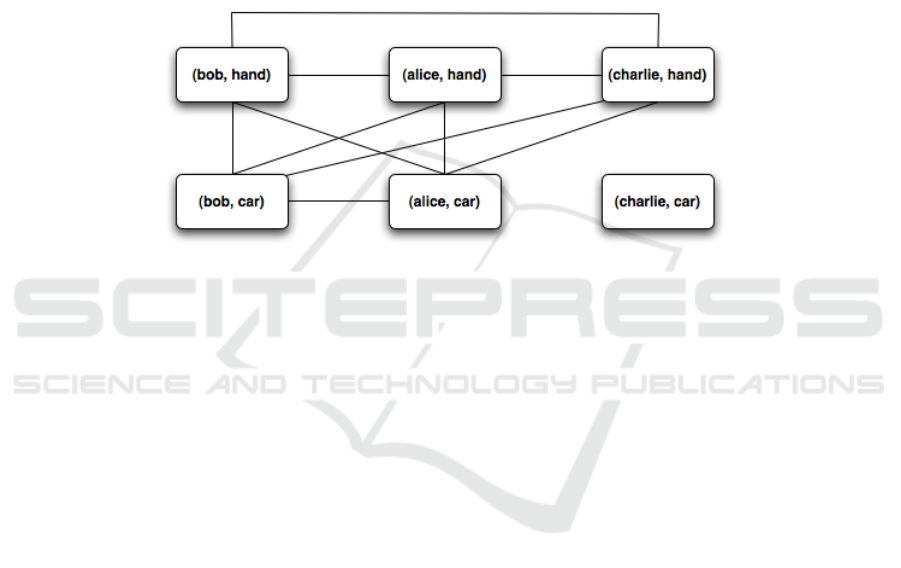
The weak change coverage graph shown in Figure 4.
Fig. 4. Coverage graph for weakChangeCoverage(c, M
c
, T ) with c = (alice, hand).
Observe that context (charlie, car) is not reachable, because it cannot be obtained
by applying any of the transformations belonging to T . Also observe that the transfor-
mation T
3
, that was originally defined to specify the context change from (alice, hand)
to (alice, car) can also be applied to change from context (bob, hand) to (bob, car).
T
1
, however, cannot be used to change from context (alice, car) to (bob, car).
We were able to derive this information by exploiting AGG’s ability to detect con-
flicts between graph transformations, based on the formal notion of critital pair anal-
ysis (CPA) [9]. Essentially, CPA enables detection of parallel conflicts between graph
transformations. Informally, a parallel conflict simply means that a given pair of graph
transformations T
a
and T
b
cannot be serialised in a particular order. More precisely,
if T
a
and T
b
can both be applied to the same host graph (with matches m
a
and m
b
,
respectively), after applying T
a
with match m
a
it is no longer possible to apply T
b
with
match m
b
. Parallel conflicts can be detected by comparing the left-hand sides of T
a
and
T
b
. An overlap between these left-hand sides implies that both transformations make
a change that is in conflict with the other one. For a more formal treatment of parallel
conflicts we refer to [10].
Coming back to our example, we observe that T
3
is applicable after T
1
, while the
opposite is not true: there is a parallel conflict between T
1
and T
3
that prevents T
1
from
being applied after T
3
for the same match. Indeed, T
3
replaces AnalogClock by Digital-
Clock while T
1
requires the presence of AnalogClock as an applicability precondition.
If we use the strong (i.e., transitive and symmetric) notion of coverage, then the
results of computing coverage(c, M
c
, T ) and the corresponding changeCoverage(c,
M
c
, T ) are shown in Figure 5.
6
It shows that the set of all contexts excluding (charlie,
6
Observe that we do not put directions on the edges because they can be followed bidirection-
ally.
15
car) forms a complete graph, implying that all dynamic context changes between these
contexts are possible. To realise this context adaptations in practice, we require that se-
quences of transformations are composable (i.e., a sequence of two context adaptations
is again a valid context adaptation), and we require that transformations are inversible
(i.e. each context adaptation can also be applied in the opposite direction). The first
property (sequential composition of parallel independent graph transformation) is au-
tomatically verified by AGG’s CPA algorithm. The second property (inversibility) is
not valid, in general, for graph transformations, and hence is not supported by AGG.
In our particular case, due to the specific way in which we have expressed our graph
transformations, their inverse can be computed directly by switching the left-hand side
and right-hand side of each graph transformation.
Fig. 5. Coverage graph for changeCoverage(c, M
c
, T ) with c = (alice, hand).
Our approach does not only allow us to verify whether a given set of contexts can
be “covered”. In addition, thanks to the fact that the context changes have been “oper-
ationalised” as sequences of graph transformations, we are also able to execute these
context changes by applying the corresponding transformation sequence. For example,
if we want to change from context (charlie, hand) to (bob, hand), we can apply the
transformation sequence T
−1
2
; T
1
. To go from (bob, car) to (alice, car ) we can ap-
ply the sequence T
−1
3
; T
1
; T
3
. A similar reasoning can be made for all other context
changes, that can be defined as a finite sequence containing only transformations con-
tained in T or their inverse.
Let us try to understand why the context (charlie, car) is not reachable, and hence
not covered by the current change-based specification of our context-sensitive applica-
tion. To this extent, we again resort to AGG’s critital pair analysis. As shown in Figure 4
we could, in principle, attain context (charlie, car) by following two possible paths
(i.e., sequences of graph transformations) starting from M
(alice,hand)
: either by apply-
ing T
2
followed by T
3
, or by applying T
3
followed by T
2
. Unfortunately, AGG’s critical
pair analysis reveals us that both sequential compositions are not allowed because their
is a critical pair conflict (of type delete-use) in both cases: the transformation T
2
(re-
spectively T
3
) deletes an AnalogClock whose presence is required as a precondition for
being able to apply the other transformation T
3
(respectively T
2
).
The only way to solve this unreachability of (charlie, car) is to manually specify an
additional fourth graph transformation T
4
that captures the ((charlie, hand), (charlie,
car)) context change. The specification of T
4
is given in Figure 6. Adding this new
16

transformation to T and computing the resulting change coverage graph will now lead
to a complete coverage graph, in which each context is reachable from each other con-
text.
Fig. 6. Additional model transformation T
4
representing the context change
((charlie, hand), (charlie, car)).
Our change-based approach provides a considerably more compact specification
of a context-sensitive application than the state-based approach. Indeed, the state-based
version of the Mobilessence specification required six context-specific models, together
with five different context changes for each of them (so 30 context changes in total). Our
change-based approach reduces this specification to only one context-specific model
and four model transformations that represent the context changes (or eight if we also
take into account the inverse transformations).
6 Discussion
It is clear from our feasibility study using graph transformation, and using AGG in
particular, that our change-based approach to dynamic context adaptation can be made
to work. However, we are aware of the fact that we have only scratched the surface
of this promising new research avenue. A lof of further work is required in order to
actually put this change-based approach into industrial practice.
A first question is what is the most appropriate approach to express context-specific
models and model transformations that represent dynamic context adaptations. The ap-
proach we presented in section 4 is independent of a particular choice of transformation
technology. The approach based on graph transformation has as its main advantage
that it provides the ability of formal reasoning. However, other formal approaches with
formal reasoning abilities, such as logic for example, could also be a good choice. A
comparison between logic-based approaches and graph transformations for the purpose
of transformation dependency analysis has been presented in [11].
A lot of formal questions remain open, such as: Which other formal properties of
graph transformation can be exploited? To which extent can the reversibility of transfor-
mations be automated? Is it possible to generate a minimal change-based specification
(consisting of an initial model and a set of model transformations) from a state-based
specification?
A disadavantage of graph transformation in particular, and formal approaches in
general, tends to be their scalability when it comes to modeling large context-sensitive
applications. For this reason, more mainstream model transformation languages such
as ATL, QVT, and Kermeta, could be used instead [12]. A comparative study of the
benefits and shortcomings of each of these languages would be needed in order to assess
their respective limitations.
17

In order to study the scalability issue in practice, we need to perform case studies
with significantly bigger context-sensitive applications. In that case, there will be a
significant number of variability dimensions (in the formal sense of Definition 1) that
we have to deal with. In addition, it is not certain that all of these dimensions will be
orthogonal, in the sense that the values in each variability are completely unrelated. If
this is not the case, it may have an important influence on the ability to sequentially
compose transformations.
7 Conclusions
In this article we presented a novel approach to model context-sensitive applications,
by relying on a change-based approach as opposed to a state-based approach. The main
idea is to reduce redundancy in the specification by expressing the context changes as
first-class model transformations. As a side effect, we get for free the ability to apply
these context changes, as well as the ability to determine the set of context-specific
models that are covered by the specification.
We motivated the potential advantages of our approach by using a small but, hope-
fully, convincing example. We provided a proof-of-concept of our approach by means
of graph transformations implemented in the AGG tool. Our proposed approach paper
opens the path for lots of further research.
Acknowledgements
We thank Mathieu Goeminne, Michael Hoste, Jorge Pinna Puissant, Alexandre Decan
and Amelie Schatteman for proofreading this article.
This work has been partially financed by (i) the Interuniversity Attraction Poles
Programme - Belgian State – Belgian Science Policy, project MoVES; (ii) the Research
Foundation – Flanders (FWO) through project G.0296.08; (iii) the research project
“Model-Driven Software Evolution”, an Action de Recherche Concert
´
ee financed by
the Minist
`
ere de la Communaut
´
e franc¸aise - Direction g
´
en
´
erale de l’Enseignement non
obligatoire et de la Recherche scientifique, Belgium; (iv) the sponsorship of the sabbat-
ical leave of Prof. Serge Demeyer.
References
1. Giuseppe Ghiani, Fabio Patern
`
o, Carmen Santoro, and Lucio Davide Spano. UbiCicero: A
location-aware, multi-device museum guide. Interacting with Computers, 21(4):288–303,
2009.
2. Gregory D. Abowd, Anind K. Dey, Peter J. Brown, Nigel Davies, Mark Smith, and Pete
Steggles. Towards a better understanding of context and context-awareness. In Proc. 1st
Int’l Symp. Handheld and Ubiquitous Computing (HUC ’99), pages 304–307, London, UK,
1999. Springer-Verlag.
3. Kris Luyten, Chris Vandervelpen, and Karin Coninx. Task modeling for ambient intelligent
environments: design support for situated task executions. In Proc. 4th Int’l Workshop on
Task Models and Diagrams (TAMODIA ’05), pages 87–94, New York, NY, USA, 2005.
ACM.
18

4. Jan Van den Bergh and Karin Coninx. Contextual concurtasktrees: Integrating dynamic
contexts in task based design. IEEE Int’l Conf. Pervasive Computing and Communications
Workshops, 0:13, 2004.
5. Reidar Conradi and Bernhard Westfechtel. Version models for software configuration man-
agement. ACM Comput. Surv., 30(2):232–282, 1998.
6. Gabriele Taentzer. AGG: A graph transformation environment for modeling and validation
of software. In Proc. AGTIVE 2003, volume 3062 of Lecture Notes in Computer Science,
pages 446–453. Springer-Verlag, 2004.
7. Nathalie Souchon, Quentin Limbourg, and Jean Vanderdonckt. Task modelling in multiple
contexts of use. In Proc. 9th Int’l Workshop on Interactive Systems. Design, Specification,
and Verification (DSV-IS’02), pages 59–73, London, UK, 2002. Springer-Verlag.
8. Oscar Nierstrasz, Jon Whittle, David Harel, and Gianna Reggio, editors. Proc. 9th Int’l Conf.
Model-Driven Engineering Languages and Systems (MoDELS’06), volume 4199 of Lecture
Notes in Computer Science. Springer, 2006.
9. Tom Mens, Gabriele Taentzer, and Olga Runge. Analysing refactoring dependencies using
graph transformation. Software and Systems Modeling, pages 269–285, September 2007.
10. Reiko Heckel. Algebraic graph transformations with application conditions. Master’s thesis,
Technische Universit
¨
at Berlin, 1995.
11. Tom Mens, G
¨
unter Kniesel, and Olga Runge. Transformation dependency analysis - a com-
parison of two approaches. S
´
erie L’objet - logiciel, base de donn
´
ees, r
´
eseaux, 2006.
12. Tom Mens. Model transformation: A survey of the state-of-the-art. In Proc. Summer School
on Model-Driven Development for Distributed Realtime Embedded Systems. ISTE, 2009.
19
