DEALING WITH IMBALANCED PROBLEMS

Issues and Best Practices

Rodica Potolea and Camelia Lemnaru

Technical University of Cluj-Napoca, Cluj-Napoca, Romania

Keywords: Imbalanced data, Sampling, Classification.

Abstract: An imbalanced problem is one in which, in the available data, one class is represented by a smaller number

of instances compared to the other classes. The drawbacks induced by the imbalance are analyzed and

possible solutions for overcoming these issues are presented. In dealing with imbalanced problems, one

should consider a wider context, taking into account the imbalance rate, together with other data-related

particularities and the classification algorithms with their associated parameters.

1 INTRODUCTION

Data mining has emerged from the practical need of

extracting useful information from large volumes of

raw data. Even if initially triggered by concrete

demands, it was quickly established as a theoretical

science, with numerous and valuable achievements.

At present, the focus is starting to shift back to the

particularities of real world problems, as data mining

moves from the status of theoretical to that of a truly

applied science. One such issue is mining

imbalanced problems, like medical diagnosis, the

detection of oil spills from satellite data or that of

fraudulent phone calls.

When dealing with imbalance problems the

traditional methods fail to achieve a satisfactory

performance, due to insufficient representation of

the minority class and because most methods focus

on maximizing the overall accuracy, to which the

minority class contributes very little (Visa, 2005).

2 PROBLEM OVERVIEW

In this paper we focus on two-class problems. The

positive class is the interest (minority) class,

containing much fewer instances than the negative

class. Initially, the difficulty of dealing with

imbalance problems was thought of coming from its

imbalance rate (IR), i.e. the ratio between the

number of negative and positive instances in the data

set.

More recent studies suggest that the nature of the

imbalance problems is actually manifold. In (Weiss,

2004), for example, two issues are considered as

being crucial: (1) between-class rarity (rare class):

insufficient data to build a model, in case the

minority class has only a few examples (similar

circumstances as in the case of small samples/small

data sets), (2) within-class rarity (rare case): too

many “special cases” in the minority class, so that in

the class itself, some kind of sub-clustering occurs,

which might lead again to insufficient examples for

correctly identifying such a sub-cluster.

For the within class imbalance, a special case is

represented by the small disjuncts problem (Holte,

1989) – the existence of “isolated” subsets of only a

few instances in the minority class, surrounded by

instances from the other class(es) (Weiss, 2004).

Another study which suggests that the origin of

the imbalance problem does not reside solely in the

rate of the data imbalance is (Japkowicz, 2002),

showing that the difficulties encountered by decision

tree learners when handling imbalanced problems

are also associated with other data characteristics,

such as data set size, or the complexity of the

problem.

Another data characteristic correlated with the

imbalance problem which affects performance is IA,

the ratio between the data set size and the number of

features. In (Potolea, 2010) we observed that a

smaller IA improves the performance of several

traditional classifiers.

443

Potolea R. and Lemnaru C. (2010).

DEALING WITH IMBALANCED PROBLEMS - Issues and Best Practices.

In Proceedings of the 12th International Conference on Enterprise Information Systems - Artiﬁcial Intelligence and Decision Support Systems, pages

443-446

DOI: 10.5220/0003019604430446

 SciTePress

3 APPROACHES FOR IDS

Out of the existing methods, some have been shown

to be affected more by the imbalance problem:

decision trees perform the worst when the data is

imbalanced ((Visa, 2005), (Weiss, 2004)), support

vector machines (SVMs) are strongly affected by the

imbalance problem, while the artificial neural

networks (ANN) are not (Potolea, 2010). Our

experimental results are in disagreement with

(Japkowicz, 2000) with respect to the behavior of

SVMs in imbalanced problems. These observations

entail an evident requirement of either adapting

algorithms to specific situations or design new ones.

The alternative solution is to alter the data

distribution such as to provide a more appropriate

distribution in the training set.

One natural solution for dealing with an

imbalance problem is to rebalance it via sampling.

Sampling techniques are grouped into two major

categories: oversampling and undersampling.

Oversampling attempts to tackle IDS by reducing

the imbalance rate in favor of the minority class, by

adding examples but this may lead to overfitting,

increase the time required to build the classifier, or

harm the learning process ((Chawla, 2004),

(Japkowicz, 2002)). Undersampling performs

rebalancing by removing examples from the

majority class which helps narrowing the search

space but may result in loss of information (García,

2009). A comprehensive study of sampling

techniques can be found in (Batista, 2004). Several

efficiently guided oversampling and undersampling

techniques are compared but none of them

dominates all the other on all data sets.

A very important issue regarding sampling

techniques refers to the appropriate volume of

over/under sampling required (Hall, 2005). A natural

question arises: is there an optimal distribution?

(Hall, 2005) suggests performing a guided search for

the correct percentage of undersampling the majority

class or synthetic oversampling the minority class.

(Weiss, 2003) proves that if there is a best

distribution for the training set, it needs more

positive examples as the dimension of the training

set decreases. (Chan, 1998) suggests we should use a

sampling technique which generates a 50-50%

distribution on several folds of the training set, in

which the minority class contains the same examples

in every fold.

Feature selection is one of the most effective pre-

processing method in enhancing the data mining

process. It not only reduces the data dimensionality,

by discarding attributes, thus reducing the search

space, but it also improves the knowledge extraction

task most of the time (Vidrighin, 2008). Moreover, it

proves to be valuable when dealing with IDS as

well, since a large number of features is most

usually accompanied by skew in the class

distribution. Feature selection could be beneficial in

such cases, by selecting the features which “can

capture the high skew in the class distribution”

(Chawla, 2004). The benefits of feature selections

have been also acknowledged in (Visa, 2005), where

it is concluded that feature selection in imbalanced

domains “is even more important than the choice of

the learning method”. Also, we have performed a

series of experiments which have shown that data

sets with a large number of instances per number of

attributes ratio (IA) behave better when faced with

the imbalanced problem (Potolea, 2010).

A step in adapting the existing algorithms to the

new conditions is to choose the most appropriate

metric for attaining the novel objective. This could

be done by analyzing the particularities of the data

and the specific problem requirements. Some

problems could require a large TP (true positives),

while others, most often require a higher

penalization for the errors which fail to identify a

positive example (i.e. false negatives). Changing the

algorithm so that examples at the boundary of the

domain are classified as belonging to the positive

class (Weiss, 2004) fosters the identification of the

positive class.

One-class learning is beneficial for imbalanced

data sets as it avoids overfitting on the majority class

(Chawla, 2004). A good method could be to

generate a model for each single class, rather than

generating a complete model with a unique strategy.

Taking this proposal further, different inducers could

be employed for learning different classes.

4 EXPERIMENTAL WORK

We have performed evaluation of the imbalance

effect on various classifiers. The performance

degradation has been traced on 9 benchmark data

sets from UCI (UCI, 2010) with 6 classifiers (k

Nearest Neighbor - kNN, decision trees – C4.5,

support vector machines – SVM, artificial neural

networks – MLP, Bayesian learning – NB and

AdaBoost ensemble learning – AB) from Weka

(Hall, 2009) with their default settings. We

performed the evaluations in a 10 fold cross

validation, by starting with the original data set and

altering the IR up to 100 by undersampling the

positive class. We measured 9 different metrics to

ICEIS 2010 - 12th International Conference on Enterprise Information Systems

444

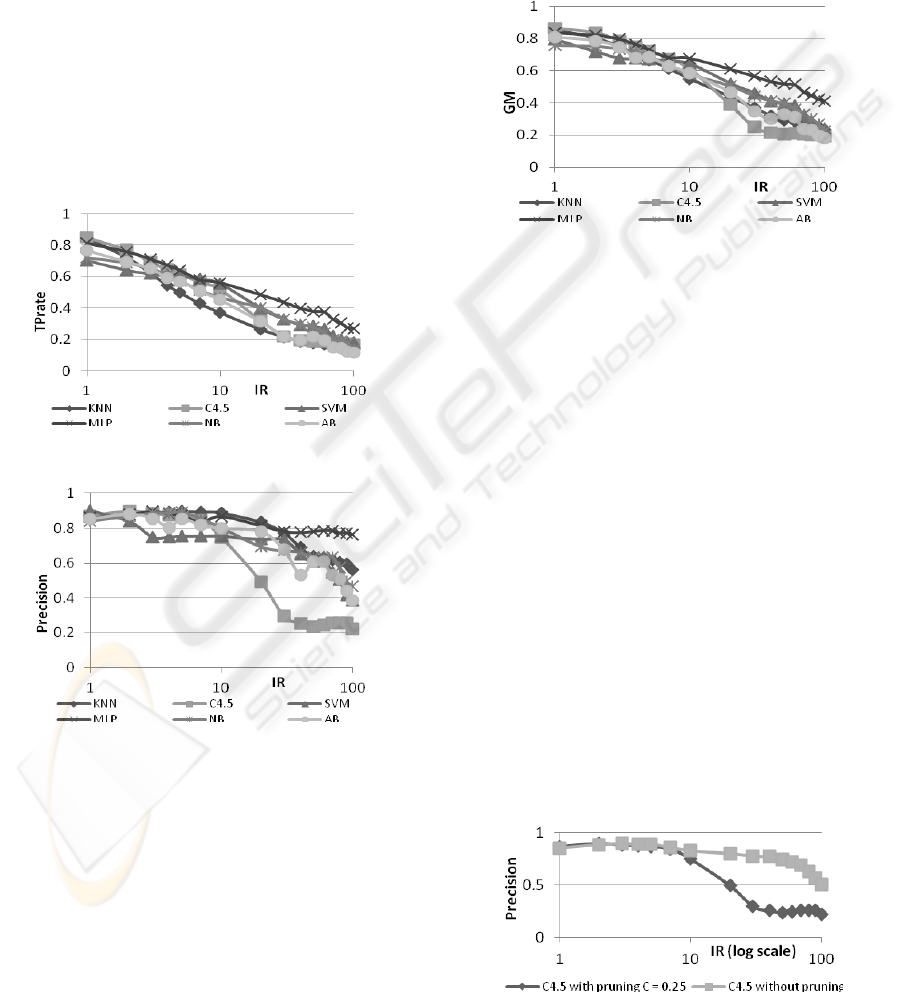
assess their suitability in the imbalance context. The

representative results are shown in Figures 1–3,

where for the x axis (IR) we chose the logarithmic

scale to better differentiate between the curves at

small IRs. Accuracy is not a good performance

indicator in case of IDS, as the degradation of

performance is much more severe than revealed by

the Accuracy. What truly interests us (Chawla,

2006) is keeping recall (TPrate) as large as possible

without degrading too much precision. Figure 1

shows a fast drop on TPrate with a recognition rate

between 0.1 and 0.3, depending on learner. This

shows that the minority class tends to become

unrecognizable. On the other hand, almost all

learners perfectly identify the majority class in case

of large imbalance (TNrates=1). This is in

accordance with (Grzymala-Busse, 2005) that

specificity doesn't work as a good indicator for IDS.

Figure 1: TPrate relative to IR.

Figure 2: Precision relative to IR.

Precision is less affected by the imbalance; however,

it degrades decision tree learners’ performance. A

good metric in case of IDS is geometric mean (GM),

capturing important aspects within a single value.

Figure 3 shows the evolution of GM while IR

increases. Similar evaluation could be done via F-

value, while in case more emphasis is put on recall,

F2-value is a better indicator. The metric we

proposed keeps the GM as main estimator,

penalizing a large difference between its

components. Our BGM metric (BGM=GM*(1-

abs(TPR-TNR)), where TPR and TNR are the true

positive and true negative rates) is important when

both classes are of interest. For all metrics evaluated

we noticed a more severe performance degradation

on C4.5 and AB, which makes them the least robust

learners when dealing with the imbalance problem.

In the same trend, yet with a smoother descend are

KNN, SVM and NB, while MLP seem to be quite

robust when dealing with imbalance.

Figure 3: GM relative to IR.

In the attempt to identify factors which affect the

most different learners, we started with the

evaluation of the decision trees. While the positive

class decreases in dimension, the number of

instances dramatically drops. In these situations,

some branches of the decision tree are characterized

by only a few instances; in such a case, the pruning

mechanism (which tends to find the most general

hypothesis) might hurt, the model generated this

way being unable to identify small subclusters

within the minority class (dealing this way with

small sample rather than the imbalance issue).

Therefore, for imbalanced problems, using the

decision tree learner without pruning could be

beneficial. We have evaluated such a possibility, by

comparing the results obtained by the C4.5 classifier

with and without pruning. According to Figure 4 the

pruning mechanism is not a beneficial one at large

IR. As C4.5 is the most affected learner when

precision is the chosen metric (Figure 2), a

specialized pruning mechanism, in accordance with

the IR is expected to generate important

improvements.

Figure 4: Precision descent on C4.5.

DEALING WITH IMBALANCED PROBLEMS - Issues and Best Practices

445

We propose intelligent pruning, which prunes

branches differently according to the number of

instances they cover. At the data level, our main

focus is on generating a combined strategy for

acquiring the best knowledge we can from the

available data: for a given data set, identify the

optimal distribution in a similar manner as (Weiss,

2003). The second step of the strategy generates

several folds out of all available data, with the

optimal distribution for each. In each fold, all the

instances from the minority class are the same (all

minority instances from the entire data set), while

for the majority class(es), we generate partitions to

reach the optimal distribution and assign one

partition per fold, so that each majority instance

occurs in a single fold. Then a model is generated

from each fold and a voting criterion is applied in

order to classify a new instance. Another point of

interest at the data level is the identification of the

appropriate IA which ensures the best performance

for a given classifier and apply a feature selection

strategy, as preprocessing step, in order to reach the

suggested IA.

5 CONCLUSIONS

To properly analyze the imbalance problem, the

relation between the imbalance and other features of

the problem, like its size and complexity

(Japkowicz, 2000), or size and IA (Potolea, 2010)

should be investigated. Secondly, since the

performance is not expected to improve significantly

with a more sophisticated sampling strategy, more

focus should be allocated to algorithm related

improvements, rather than to data improvements.

Finally, starting from the observation that there is no

winner (neither in terms of sampling, nor algorithm)

for all data sets, special attention should be paid to

the particularities of the data at hand. That is, to

apply various tuning strategies for finding the

appropriate combination of learning technique and

sampling strategy, while in a following step, finding

the best settings for them: parameter values, function

selection, threshold, distribution, and many others,

specific to the technique.

ACKNOWLEDGEMENTS

This work was supported by the IBM Faculty Award

received in 2009 by Rodica Potolea from the CS

Department of TUCN Romania.

REFERENCES

Batista, G., Prati R., and Monard M., 2004, A Study of the

Behavior of Several Methods for Balancing Machine

Learning Training Data. SIGKDD Explorations, 6:20-

24, Volume 6, Issue 1, pp. 20-29.

Chan, P., and Stolfo, S., 1998, Toward scalable learning

with non-uniform class and cost distributions: a case

study in credit card fraud detection. In Proceedings of

the Fourth International Conference on Knowledge

Discovery and Data Mining, Menlo Park, CA: AAAI

Press, pp. 164-168

Chawla, N.V., Japkowicz, N. and Kolcz, A., 2004,

Editorial: special issue on learning from I imbalanced

data sets, SIGKDD Explorations Special Issue on

Learning from Imbalanced Datasets 6 (1), pp. 1–6.

Chawla, N. V., 2006 Data Mining from Imbalanced Data

Sets, Data Mining and Knowledge Discovery

Handbook, chapter 40, Springer US, pp. 853-867.

Grzymala-Busse, J. W., Stefanowski, J., and Wilk, S.,

2005, A comparison of two approaches to data mining

from imbalanced data, Journal of Intelligent

Manufacturing, 16, 2005 Springer Science+Business

Media, Inc. Manufactured in The Netherlands, pp.

565–573.

Hall, L. O., and Joshi, A., 2005, Building Accurate

Classifiers from Imbalanced Data Sets, IMACS’05.

Hall, M., et.alt., 2009, The WEKA Data Mining Software;

SIGKDD Explorations, Volume 11, Issue 1.

Holte, R. C., Acker, L. E., and Porter., B. W., 1989,

Concept learning and the problem of small disjuncts.

In Proceedings of the Eleventh International Joint

Conference on Artificial Intelligence, pp. 813-818.

Japkowicz, N., 2000, The Class Imbalance Problem:

Significance and Strategies, in Proceedings of the

2000 International Conference on Artificial

Intelligence (IC-AI'2000), pp. 111-117.

Japkowicz, N., and Stephen, S., 2002, The Class

Imbalance Problem: A Systematic Study, Intelligent

Data Analysis Journal, Volume 6, Number 5,

November 2002, pp. 429 – 449.

Potolea, R., and Lemnaru, C, 2010, The class imbalance

problem: experimental study and a solution, paper

submitted for ECMLPKDD 2010.

UCI Machine Learning Data Repository, 2010,

http://archive.ics.uci.edu/ml/, last accessed Jan. 2010.

Vidrighin Bratu, C., Muresan T., and Potolea, R., 2008,

Improving Classification Accuracy through Feature

Selection, in Proceedings of the 4th IEEE

International Conference on Intelligent Computer

Communication and Processing, ICCP 2008, pp. 25-

32.

Visa, S., and Ralescu, A., 2005, Issues in mining

imbalanced data sets -a review paper, in Proceedings

of the Sixteen Midwest Artificial Intelligence and

Cognitive Science Conference, pp. 67–73.

Weiss, G., and Provost, F., 2003, Learning when Training

Data are Costly: The Effect of Class Distribution on

Tree Induction. Journal of Artificial Intelligence

Research 19, pp. 315-354.

Weiss, G., 2004, Mining with rarity: A unifying

framework, SIGKDD Explorations 6(1), pp. 7–19.

ICEIS 2010 - 12th International Conference on Enterprise Information Systems

446