Metamodels Matching: Issue, Techniques and

Comparison

Lamine Lafi

, Wajih Alouini

, Slimane Hammoudi

and

Mohamed Mohsen Gammoudi

ISSAT, Université de Sousse, Sousse, Tunisia

FST, Faculté des Sciences de Tunis, Tunis, Tunisia

ESEO, Ecole supérieure de l’Ouest Angers, France

Abstract. Research and practice for Model Driven Engineering (MDE) have

significantly progressed over the last decade for dealing with the increase of

complexity within systems during their development and maintenance

processes by raising the level of abstraction using models as information

storage. New significant approaches, mainly Model Driven Architecture

(MDA) defined at the OMG (Object Management Group), “Software Factories”

proposed by Microsoft and the Eclipse Modeling Framework (EMF) from IBM,

are born and have been experimented. As models grow in use for developing

systems, transformation between models grow in importance. University and

industry are seeking for effective and efficient ways to treat transformation as

first-class assets in MDE. In order to produce new and more powerful

transformations, we argue that the semi-automatic generation of transformation

rules is an important challenge in future MDE development to make it easier,

faster, and cost-reduced process. In this paper we propose to discuss

metamodels matching as a key technique for a semi-automatic transformation

process. We review, compare, and discuss the main approaches that have been

proposed in the state of the art for metamodels matching.

1 Introduction

The special interest behind model driven engineering (MDE) is on the promise of

tackling the increase of complexity within the software and its development process

by raising the level of abstraction using models as information storage. With the aim

of making models as the available internal information, academy and industry have

provided several MDE based approaches, among which the most well known are

MDA [1] by OMG , “Software factories” by Microsoft [2] and the Eclipse Modeling

Framework (EMF) from IBM [3]. MDE has transferred the focus of work from

programming to modeling by treating models as first class entities and consequently

the primary artifacts of development. As a consequence, models had to be handled

and therefore opened new axis of research on the model transformation even if

transformation existed in research fields prior to MDE [4]. In the literature, several

issues around MDE have been studied and subject of intensive research, e.g. modeling

Laﬁ L., Alouini W., Hammoudi S. and Mohsen Gammoudi M.

Metamodels Matching: Issue, Techniques and Comparison.

DOI: 10.5220/0003026300200034

In Proceedings of the 2nd International Workshop on Future Trends of Model-Driven Development (ICEIS 2010), page

ISBN: 978-989-8425-10-2

languages [4] [5], model transformation languages [6] [7], mapping between

metamodels [8] [9], Scalability and reuse of model transformations [10], Maintenance

and evolution of model transformations [11] and Model-driven development

methodologies, approaches, and languages with a focus on transformations [12]. Of

particular interest to transformation among these issues, are model transformation

languages that allow defining how a set of elements from a source model are analyzed

and transformed into a set of elements of a target model, the output of transformation

being a set of rules involving, and in the same time merging mapping and

transformation techniques between two metamodels. Now that the treated information

becomes available as models, the problem of a manual transformation still exists, and

is one of the main barriers to tackle avoiding making transformation fastidious and

error-prone task, and therefore an expensive process. The semi-automatic generation

of transformation rules is an important challenge in future MDE development to make

it easier, faster, and cost-reduced process with the decrease of errors that may occur.

Matching techniques between metamodels are the centerpieces for a semi-automatic

transformation process in MDE and particularly in MDA. In fact, metamodels

matching allows discovering mappings between two metamodels and the mappings

allow in turn generating transformation rules between two metamodels. However,

there has been little research in metamodel matching. In the database domain, the

corresponding term for metamodel matching is schema matching. In this paper, we

discuss the problem of schema matching that has been extensively studied in the

database area, and then we review the main different approaches that have been

proposed for metamodel matching in the context of MDA/MDE. We will start by

stressing the role of matching techniques in the semi-automatic process of model

transformation.

This paper is organized as follows: section 2 introduces the main concepts and

techniques for a semi-automatic transformation process, presents schema matching

techniques and situates it in the context of metamodel matching. Section 3, reviews

and compares five approaches that have been proposed for metamodel matching in

the context of MDA. Finally, section 4 concludes our work and presents some final

remarks and perspectives.

2 Metamodels Matching for Model Transformation

2.1 Metamodels Matching for Model Transformation: Overview

It is well recognized today that model transformation is one of the most important

operations in MDA [13]. The following definition of model transformation, largely

consensual, is proposed in [14]:

“A Transformation is the automatic generation of a target model from a source

model, according to a transformation definition. A transformation definition is a set

of transformation rules that together describe how a model in the source language

can be transformed into a model in the target language. A transformation rule is a

description of how one or more constructs in the source language can be transformed

into one or more constructs in the target language”.

However, we point out two main problems concerning the MDA transformation

process.

• The first problem concerns the manual creation of “transformation rules” between

metamodels. Generally, this task is tedious and error-prone, and therefore

expensive in terms of efficiency [15]. Moreover, writing the transformation rules

requires a good mastery of both the transformation language and the source and

target metamodels, in order to express the correspondence both from a structural

and a semantic point of view.

• The second problem concerns the specification of these “transformation rules”,

which merge together techniques of mapping and transformation without an

explicit distinction between them. That is to say, the specification of

correspondences between elements of two metamodels and the transformation

between them are grouped in the same component at the same level.

In the MDA context, and according to previous works [10, 16], the concepts of

mapping and transformation should be explicitly distinguished, and together could be

involved in the same process that we call transformation process. In fact, in the

transformation process, the mapping specification precedes the transformation

definition. A mapping specification is a definition of the correspondences between

metamodels (i.e. a metamodel for building a PIM (Platform Independent Model) and

another for building a PSM (Platform Specific Model)). This definition is largely

obtained by a matching process between two metamodels, and completed by an

expert. Transformation definitions contain an explicit description of how to transform

a model into another using a transformation language. Transformation definitions are

a set of rules that are obtained automatically from all the mappings between two

metamodels. Hence, in our approach the transformation process of a PIM into a PSM

can be structured in two stages: a mapping specification obtained by a matching

process and completed by an expert, and a transformation definition derived

automatically from the mappings.

The figure 1 illustrates the main concepts and techniques involved in a semi-

automatic transformation process. The matching operation is the process that

produces the potential mappings between two metamodels. Generally, this task

implies a search of equivalent or similar elements between two metamodels. Given

that no generic matching solution exists for different metamodels and application

domains, it is recommended to give the human expert the possibility to check the

obtained mappings, and, if necessary, update or adapt it. This is one of the steps in

the whole process, in which the expert intervenes to complete and validate the

obtained results. Finally, a transformation model (a program: a set of rules), is derived

automatically from a mapping model. A transformation model is basically represented

by a set of rules that states how elements from source metamodel are transformed into

elements of target metamodel. A transformation model (program) takes a source

model defined by designers or and produces an equivalent target model on a specific

platform.

Two important operations (dashed arrows) adaptation (1) and derivation (2) allow

linking and completing the two main operations (matching and transformation) in the

whole process of transformation. Adaptation is the responsibility of the expert user

who should accept, discard or modify the obtained mappings, furthermore, to specify

the correspondences which the matcher was unable to find. Loosely speaking, the

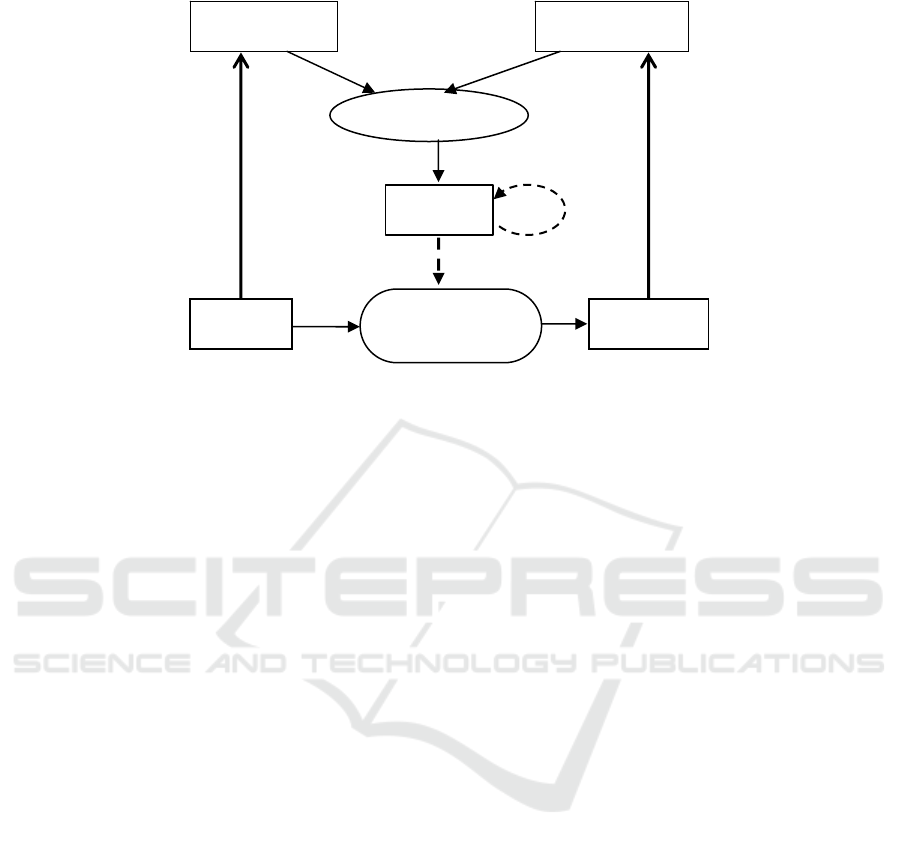
Fig. 1. Semi-automatic transformation process.

mapping and matching techniques (models) could be defined with the following

intuitive formula:

Mapping = Matching + Adaptation

The mapping model obtained in the previous step after adaptation by the expert user

should be completely defined allowing an automatic generation of transformation

model. This operation is called derivation and, in the same way as above,

transformation and mapping models can be defined with the following intuitive

formula:

Transformation = Mapping + Derivation

2.2 From Schema Matching to Metamodel Matching

Matching between metamodels are the centerpieces for a semi-automatic

transformation process in MDE, particularly in MDA. Matching techniques have been

studied in various research domains, including digital libraries, ontologies, agent

matchmaking, schema integration and evolution in databases [16] [17]. In the context

of MDE, we can find few works in the literature that address the problem of

metamodels matching. Schemas in the context of databases and metamodels in our

context of MDE are closely related, hence, we propose to review the different

approaches of schema matching, and after that we situate these approaches in our

context of metamodeling matching.

2.2.1 Classification of Schema Matching Approaches

In the literature, several schema matching approaches have been proposed [16] [17].

Each schema matching approach has its own characteristics that were grouped in a

taxonomy illustrated bellow in figure 2 [15] [18]. In addition, each approach has been

Source

Metamodel

Target

Metamodel

Matching Techniques

Mapping

Model

Transformation

Model

(program)

Source

model

Target

model

(1)

(2)

Fig. 2. Classification of schema matching approaches.

evaluated through match quality measures discussed in the next section 2.2.2.

• Individual matcher approaches use only one matching criterion. They are

classified in:

– Schema-only based, when they consider only metamodels. They can be classified in:

9 Element level, the mapping is realized for each individual element. It can be

classified in linguistic and constraint-based. Linguistic are based on name

similarity, description, global namespace, while constraint-based are based on

type similarity and key properties.

9 Structure-level, the mapping is realized considering the combinations of

elements related in a structure. It is only classified in constraint-based that use

graph matching.

– Instance/contents-based, when they consider only instances (or models). It can also

be classified in element-level. This last can be classified in linguistic and

constraint-based. In this case, linguistic is based on word frequencies and key terms

present in the element instances, while constraint-based is based on value pattern

and ranges of the element instances.

• Combining matchers use multiple matching criteria. They can be classified in:

– Hybrid, they combine multiple approaches to create only one matcher in order to

produce a result, i.e. the creation of mapping between elements.

– Composite, they combine many results obtained from different approaches in

order to produce the mapping between elements. This combination of results can

be manual or automatic.

2.2.2 Matching Quality Measure

The interrelationships between metamodels can be organized in sets which can be

manually or automatically created. A set created manually can contain all needed

matches (i.e. matched elements); while a set created automatically can contain valid

and non valid matches. The first set is denominated real matches, and the later derived

matches (cf. Figure 3).

Schema Matching Approaches

Individual matcher

approaches

Combining

matchers

Schema-only

base

Instance

contents-base

Hybrid

matchers

Composite

matchers

Element-

level

Structure-

level

Element-

level

Manually:iterative

user feedback

Structure-

level

Fig. 3. Comparing real matches and automatically derived matches.

In addition, other subsets are defined as follows [16] [18]:

- A (false negatives) are matches needed but not automatically identified.

- B (true positives) are matches which are needed and have also been correctly

matched by the automatic match operation.

- C (false positives) are matches falsely proposed by the automatic match operation.

- D (true negatives) are false matches which have also been correctly discarded by

the automatic match operation.

Based on the cardinalities of these sets, the following match quality measures are

provided as parameters for benchmarks:

Precision =

reflects the share of real correspondences among all found

ones.

Recall =

specifies the share of real correspondences that are found.

F-Measure = 2 *

Pr *Re

Pr Re

ecision call

ecision call+

Overall = Recall * (1 -

ecisionP

)

All these measures were developed specifically in the schema matching context [15]

[18]. We can notice that F-Measure represents the harmonic mean of Precision and

Recall. The main underlying idea of Overall is to quantify the post-match effort

needed for adding missed matches and removing false ones.

2.2.3 Metamodel Matching versus Schema Matching

Our aim is not to compare schema matching approaches with those of metamodel

matching. The main reason is that the technological spaces of both approaches are not

the same. A technological space [19] is a working context with a set of associated

concepts, body of knowledge, tools, required skills, and possibilities. It is often

associated to a given user community with shared know-how, educational support,

A B C

Real Matches

Derived Matches

common literature and even workshop and conference regular meetings. Although it

is difficult to give a precise definition, some TSs can be easily identified, e.g. the

XML TS, the DBMS TS, the abstract syntax TS, the meta-model (OMG/MDA) TS,

etc. In one case, in schema matching efforts have been made mainly in the context of

databases and involve ER schemas. In the other case, metamodel matching focuses on

UML OMG standard which is structurally and semantically richer than ER schemas.

Moreover, the level of abstraction of metamodels and schemas is not the same.

However, techniques known and used to find semantic correspondences between the

elements of two schemas are to be applied to the metamodel matching problems since

the aim “finding semantic correspondences” is still the same. We can say that

metamodel matching techniques would probably subsume schema matching

techniques from the fact that a technological space of metamodels includes the

technological space of schemas in database area. Thus metamodel matching

techniques will probably become a generic solution to many problems of matching;

that we can call the X-matching.

3 Metamodel Matching: A Review and Comparison

In this section we will review and compare the different approaches of metamodels

matching presented respectively in [20], [21], [18], [17], [15], and [22] as well as their

evaluations. We have encountered a number of systems, which have not been

evaluated altogether, respectively SF, SAMT, ModelCVS, Delfabro, and Extended

SAMT4MDE.

3.1 A review for Metamodel Matching

3.1.1 Similarity Flooding SF

System Description. SF [20] converts schemas (SQL DDL, RDF, XML) into labeled

graphs and uses fix-point computation to determine correspondences of 1:1 local and

m: n global cardinality between corresponding nodes of the graphs. The algorithm has

been employed in a hybrid combination with a simple name matcher, which suggests

an initial element-level mapping to be fed to the structural SF matcher. Unlike other

schema-based match approaches, SF does not exploit terminological relationships in

external dictionary, but entirely relies on string similarity between element names. In

the last step, various filters can be specified to select relevant subsets of match results

produced by the structural matcher.

Similarity Flooding in [21] is a generic alignment algorithm that allows calculating

the correspondences between the nodes of two labeled graphs. This algorithm is based

on the following intuition: if two nodes stemming from two graphs have been

determined as similar, therefore, there would be strong opportunities for the

neighboring nodes to be similar, too. More precisely, SF applies five successive

phases on the labeled graphs which have been provided at the input phase. This

algorithm is applied after the transformation phase that consists in transforming the

MMsource and the MMtarget to the directed labeled graphs Gsource and Gtarget. Along this

phase a set of six strategies to encode the metamodel into such a graph has been used.

Each of these strategies has got its proper techniques to transform these two models

into a graph.

Evaluation. The SF evaluation in [20] used 9 match tasks defined from 18 schemas

(XML and SQL DDL) taken from different application domains. The schemas were

small with the number of elements ranging from 5 to 22, while showing a relatively

high similarity to each other (0.75 on average). Seven users were asked to perform the

manual match process in order to obtain subjective match results. For each match

tasks, the results returned by the system were compared against all subjective results

to estimate the automatic match quality, for which the Overall measure was used.

Fig. 4. Match quality of Similarity Flooding Algorithm [20].

Other experiments were also conducted to compare the effectiveness of different

filters and formulas for fix-point computation, and to measure the impact of

randomizing the similarities in the initial mapping on match accuracy. The best

configuration was identified and used in SF. Figure 4 shows the Overall values

achieved in the single match tasks according to the match results suggested by the

single users. The average Overall quality over all match tasks and all users is around

0.6.

Referring to the experiments [21] it is noticed that in each of the six mentioned

strategies, a set of match quality variable from one strategy to another is obtained.

The results show that the best configuration is generally saturated. On the other hand,

the Minimal configuration gives very bad results. Full and Standard configurations,

despite using more information from the metamodels, seem to produce slightly poorer

results than the Basic configuration. The metamodels used to match on Ecore vary in

size. Minjava has more or less the same size as Ecore, Kermeta is a little bigger, and

UML is very large. We can clearly see from the results that the alignment quality

decreases when the size difference between the two matched metamodels is

increasing. This is partly caused by the Selected Threshold filter that the alignment

produced by Similarity Flooding. Results on Ecore↔Minjava and Ecore↔Kermeta

show that good quality alignments can be produced by this approach as described by

the figures 11 and 12 in [21].

3.1.2 ModelCVS

System Description. In [18], the authors propose an approach said “lifting”, allowing

to transform the source and target metamodels into equivalent ontologies. This

approach proposes a framework of matching the metamodels thanks to a transition of

ModelWare into OntoWare while using transformations of the metamodels Ecore-

based into OWL-based ontologies. After having done this transition, one can reuse the

tools of ontologies matching that exploit the ontologies which really represent the

metamodels. Once the matching task is over, the transition of the ontology mapping

into a model of texture will be done. From this model of texture, the necessary

transformation rules to transform some models in conformity with a metamodel A to a

model in conformity with a metamodel B can be deduced.

In this work, they concentrate on evaluating schema-based matching tools, i.e., they

do not consider instance-based matching techniques. This is due to the fact that they

are using the data provided by metamodels (schema-level) and not data from models

(instance-level) to find equivalences between metamodel elements.

Evaluation. According to [18], in addition to the different modifications and

combinations of different matching techniques which produce higher precision values

but at the same time lower recall values, the Metamodels must fullﬁl some

requirements in order to prove that matching tools are worth using. The 10 integration

scenarios showed that the metamodels must have a common terminology and

taxonomy, which is the case when matching UML1.4, UML2.0 and Ecore. These

combinations lead to the best results despite their size which obviously lead to a

higher number of elements that have to be matched. Furthermore, good results are

achieved when matching WebML with EER. These two metamodels also have a

common terminology and both do not heavily use inheritance relationships. In

contrast, matching WebML or EER with UML1.4, UML2.0 or Ecore results in a very

low precision and in a very poor recall which is mostly below 0.10.These results lead

to the conclusion that Ontology matching tools are not always appropriate for

matching metamodels. Instead, the metamodels must fullﬁl some common properties

which of course are not always the case when matching real-world metamodels.

The evaluation of [18] produced the following best average match quality:

Precision=0.63, Recall=0.68, F-Measure=0.61. This last measure is used to study the

impact on match quality (>0.5 indicates positive benefit, <0.5 indicates negative

benefit)

3.1.3 SAMT4MDE

System Description. In [17], the authors have discussed some issues of schema

matching and provided some insights into metamodel matching. To reach this end,

they have used UML and the C# platform to illustrate their approach and to evaluate

their Mapping Tool for MDE (MT4MDE) and Semi-Automatic Matching Tool for

MDE (SAMT4MDE).

Their approach takes into account metamodel matching in the context of MDE. The

study of metamodel matching in MDE is a promising trend to improve the creation of

mapping specification and, consequently, the transformation definition. Tools for

metamodel matching are necessary to avoid error-prone factors linked to the manual

creation of the transformation definition and to evolve mapping specification when

metamodels change.

Metamodel matching results in a mapping model, which describes how two

metamodels are related to each other. According to model management algebra [23],

a mapping is generated using an operator called match which takes two models as

input and returns a mapping between them. This operator has been modified as

follows: given M

a, Mb and CMa→Mb / Mc, the operator match is formally defined as:

Match’(Ma,Mb)= CMa →Mb / Mc.

Evaluation. The evaluation of this approach [17] resulted in the following values

- Schema similarity SS =0.74

- Match quality measures: Precision =0.71, Recall =0.68, F-Measure =0.69, Overall

=0.40

In the ideal case, Precision=Recall=1.0, i.e. when the number of false negatives and

false positives are both zero. In this experimentation, Precision =0.71 demonstrates

that 71% of derived matches were correctly determined using our schema matching

algorithm. And Recall =0.68 demonstrates that 68% of real matches were

automatically found.

3.1.4 Heuristics for Transformation

System Description. In [15], authors suggest different heuristics for the realization of

matching between two metamodels. The Match operation takes two models M

a and

Mb as input and produces a weaving model Mw as output. Ma and Mb conform to MMa

and MM

b; Mw conforms to MMw.

w: MMw= Match (Ma:MMa, Mb:MMb) (1)

These heuristics use matching transformations and weaving models to semi-automate

the development of transformations. As defined in [15], Matching transformations are

a special kind of transformation which implements heuristics and algorithms to create

weaving models. Their function is also to select a set of elements from a group of

input models and to produce links between these elements. Following the same line of

thought, weaving models are models that capture different kinds of relationships

between models. The solution suggested earlier enables to rapidly implement and

customize these heuristics. Different heuristics are combined and a new metamodel-

based heuristic is proposed to exploit metamodel data which automatically produce

weaving models and also to exploit the internal features of the set of input

metamodels in order to produce weaving models which are derived into model

integration transformations. This heuristic is executed together with a link rewriting

method that analyzes the weaving metamodel extensions to produce frequently used

transformation patterns.

Evaluation. The matching transformations in [15] are executed with two variations of

the motivation example. In the first example, MM1 and MM2 conform to KM3. In the

second example, MM1 conforms to KM3 and MM2 conforms to SQL-DDL. The

weaving models are translated into model transformations. The goal is to verify if the

transformations are generated correctly, and to verify if the matching transformations

can be easily adapted in both examples.

3.1.5 Extended SAMT4MDE

System Description. The contribution of [22] to this ﬁeld of metamodel matching is

an algorithm that uses structural comparison between a class and its neighbouring

classes in order to select the equal or similar classes from source and target

metamodels. The proposed algorithm for metamodel matching is an extension and

enhancement of the algorithm presented in [24] and it is implemented in the Semi-

Automatic Matching Tool for MDE (SAMT4MDE) which is capable of semi-

automatically creating mapping specifications and making matching suggestions that

can be evaluated by users. This provides more reliability to the system because

mapping becomes less error-prone. The algorithm proposed can identify structural

similarities between metamodel-elements. However, sometimes elements are matched

by its structures but they do not share their meanings. The lack of analysis about

element meaning leads the tool to find false positives, i.e. derived correspondences

that are not real.

Evaluation. The evaluation of [22] uses a test case for creating mapping specification

between UML and Java metamodels in order to evaluate the algorithm developed in

this paper for metamodel matching. The SAMT4MDE produced the following results

for this study case: Schema similarity=0.68, Precision=0.84, Recall=0.90, F-

Measure=0.87 and Overall=73.

The similarity between UML and Java metamodels is 0.68. This means that 68% of

elements from both metamodels are involved in metamodel matching. A high

percentage of metamodel similarity means that semantic distance between these

metamodels is small, and low percentage means the opposite.

The measure of precision is 0.84. It is assumed from this information that 84% of

found correspondences are correct. The measure of recall is 0.90, meaning that 90%

of existing correspondences were found.

3.2 Comparison between Metamodel Matching Techniques

Table 1 gives a summary of the discussed evaluations. Unlike other approaches of

schema matching, the five studied approaches of metamodels matching do not exploit

terminological relationships in an external dictionary, but entirely rely on string

similarity between elements.

Comparing these approaches, we have found some similarities and differences

between them. SAMT4MDE [17], ModelCVS [18] and Extended SAMT4MDE[22]

use an object oriented model as schema type, while the other approaches/tools such as

SF and Delfabro [15] use an object oriented model and relational or XML as schema

type.

SF and SAMT4MDE [17] use small metamodels, while ModelCVS [18] and [15] rely

on large and even very large size schemas.

According to Table 1, SF allows only eighteen schemas per nine match task (18/9

schemas/task), and SAMT4MDE allow only two schemas per match task (2/1

schemas/task).

In SAMT4MDE [17] the schema similarity is the highest (equal to 0.79) compared

to the other approaches while in Extended SAMT4MDE [22] it is equal to 0.68.

SAMT4MDE [17] uses discrete values {-1, 0, 1} as match result representation

(i.e. different, similar or equal), while the other approaches (SF, ModelCVS,

Extended SAMT4MDE) use continuous values in the range [0, 1] to represent the

similarity degree. For Delfabro [15], the matches are not mentioned.

The metadata representation of SF and SAMT4MDE are nodes which represent a

metamodel, while Kappel (ModelCVS project) and Delfabro represent models or

metamodels data. In Extended SAMT4MDE [22] an UML diagram class has been

studied.

All approaches with the exception of Delfabro [15] provide a match local

cardinality of 1:1, and a match global cardinality of 1: n, while SAMT4MDE provides

a match cardinality of 1:n.

The employed quality measure in SF is overall, in ModelCVS [18] these measures are

Precision, Recall, and F-measure. SAMT4MDE and Extended SAMT4MDE use the

same measures (Precision, Recall, Overall, F-measure), while Delfabro[15] utilizes

Element similarity, link rewriting and link filtering.

SF in [20] has taken into consideration the subjectivity of the user’s perception vis-

à-vis the necessary correspondences (7 users), in [21] it has used 6 configurations.

The evaluation of ModelCVS [18] has used 10 scenarios and 13 settings tools,

SAMT4MDE [17] has used 02 fragments of UML and C-sharp metamodels, [15] has

utilized a set of input Metamodels. Finally, Extended SAMT4MDE [22] has utilized

one class and its neighboring classes.

All the approaches do not necessitate any pre-match effort. The exception is in SF,

where there is an intervention of the user in the choice of metamodels alignment and

the necessary tools in [20] [21].

To study the impact match quality, SF utilizes a fix-point (Filters), ModelCVS

utilizes F-measure (>0.5 positive benefit ;< 0.5 negative benefit), Extended

SAMT4MDE uses a threshold; while for SAMT4MDE and ModelCVS [15] it is not

mentioned.

Extended SAMT4MDE provides the Highest best average match quality,

(precision=0.84, Recall=0.90, F-measure=0.87, and overall=0.73) compared to

SAMT4MDE (precision=0.79, Recall=0.68, F-measure=0.73, and overall=0.49), and

ModelCVS (precision=0.63, Recall=0.58, F-measure=0.61). For SF [20] Overall is

almost equal to 0.6, while in [21] these measures vary from one configurations to

another.

The Application area for SF is the database and ontologies, while for ModelCVS

[18] it is the database and structural modeling languages. SAMT4MDE focuses on

model transformation, and for Delfabro [15] it is the Database and model

transformation. Finally, the Application area for Extended SAMT4MDE is the

database (Database integration, E-business and Data warehouse).

The manual work of the user is especially required in SF. It consists in choosing the

metamodels to align, evaluating the matching suggestions produced by the algorithm.

The latter task can equally be applied to Extended SAMT4MDE. In ModelCVS [18]

the user’s intervention consists in including ontology creation tools, query tools,

matching tools, and Reasoning tools.

Table 1. Summary of the evaluations.

SF ModelCVS SAMT4MDE Extended

SAMT4MDE

References

[20]&

[21]

[18] [17] [15] [22]

Test problems

Tested

Schema types

XML/SQL DDL

Relational/RDF/

UML/ Ecore

UML1.4/UML 2.0 Object-oriented

model: UML, Java,

and C-Sharp

SQL DDL

Relational/

UML

UML 2.0/

Ecore

Schema /

Schema tasks

18/9 - 2/1 - -

Min /Max /

Avg schema

size

5/22/12 Large schema Very large

schema

Min /Max /

Avg schema

similarity

0.46/0.94/0.75 - Schema

similarity=0.79

- Schema

similarity=0.68

Match result representation

Matches

Element-level correspondences between

similarity value in [0.1]

With discrete value

{0,1,-1}

Similarity

value in [0.1]

Element Repr Node Models/Metamodels Node

Models or

Metamodels

Data

Class

Local/Global

Cardinality

1:1/m:n 1:1/m:n 1 :n - 1:1/m:n

Quality of measure And test methodology

Employed

Quality

Measures

Overall

Precision, Recall, F-

measure

Precision, Recall,

Overall, F-measure

Element

similarity*,

Link filtering,

Link rewriting.

Precision,

Recall,

Overall,

F-measure

Subjectivity

7 user/ 6

configurations

10 scenarios and 13

tools settings

02 Fragments of

UML and C#

metamodels

A set of input

metamodels

1 class and its

neighbor

classes

Pre-match

effort

None None None None None

Studies Impact

on match

Quality

Filters, fix-point

formulas,

randomizing initial

similarity

F-Measure:

IF>0.5: positive

benefit

IF<0.5: negative

Benefit

Threshold

Best average Match quality

Prec/ Recall

0.63/0.58 0.79/0.68 - 0.84/0.90

F-measure 0.61 0.73 - 0.87

Overall ˜0.6 - 0.49 - 0.73

Evaluation high light

User subjectivity, no

pre-match effort

no pre-match effort

Representative

metamodels for

developing

information system

no pre-match

effort

no pre-match

effort

Application

Area

Database and

ontologies

Database and

Structural Modeling

languages

Model

transformation

Model

transformation

Model

Transformation

Manual work

of user

Choice of

metamodels to align,

Evaluate matching

suggestions produced

by algorithm.

Including ontology

creation tools, query

tools, matching

tools, and Reasoning

tools.

Evaluate

matching

suggestions

produced by

algorithm

Match

granularity

Element level

Mapping

Schema-level

Matching

Schema-level

Matching

- -

* Contains element to element similarity and structural similarity

** Change from configuration to another

SF has a granularity of matching at element level; otherwise ModelCVS [18] and

SAMT4MDE [17] have a granularity of matching at structure level.

The majority of these approaches have a combination of matches of type hybrid.

4 Conclusions

A semi-automation of the transformation process in MDE/MDA leads to a real

challenge allowing many advantages: it enhances significantly the development time

of transformation and decreases the errors that may occur in a manual definition of

transformations. Matching techniques between metamodels are the centerpieces for a

semi-automatic transformation process in MDE/MDA. The contribution of this work

is twofold: First, we present the main techniques and artifacts involved in the semi-

automatic transformation process. Second, we review five main approaches that have

been proposed in the literature for metamodel matching. In the future work, we will

concentrate on how to combine different approaches to enhance the matching process.

In addition, we will envisage studying the optimization of mapping models which

seems to be another important issue in MDE.

References

1. OMG, 2001. Model Driven Architecture (MDA)- document number ormsc/2001-07-01.

(2001).

2. Dominguez, K., Pérez, P., Mendoza, L., Grimán, A., 2006. Quality in Development Process

for Software Factories According to ISO 15504, In CLEI electronic journal,

[http://www.clei.cl, Vol. 9 Num. 1 Pap. 3: June 2006.

3. Budinsky, F., Steinberg, D., Merks, E. , Ellersick, R., Grose, T. J., 2003. Eclipse Modeling

Framework: A Developer’s Guide, Addison-Wesley Pub Co, 1st édition.

4. Bézivin, J., 2005. On the Unification Power of Models. In Software and Systems Modeling,

4(2):171-188.

5. Booch, G. Brown,A Iyengar, S Rumbaugh, J and Selic, B. An MDA Manifesto. MDA

Journal, May 2004.

6. Jouault, F., 2006. Contribution à l'étude des langages de transformation de modèles, Ph.D.

thesis (written in French), University of Nantes.

7. OMG, 2005. MOF QVT Final Adopted Specification, OMG/

2005-11-01.

8. Hammoudi, S., Janvier, J., Jouault, F., Lopes, D., 2005. Mapping Versus Transformation in

MDA: Generating Transformation Definition from Mapping Specification, In VORTE

2005, 9th IEEE International Enterprise Distributed Object Computing Conference.

9. Hammoudi, S., Lopes, D., 2005. From Mapping Specification to Model Transformation in

MDA: Conceptualization and Prototyping. In MDEIS’2005, First International Workshop.

10. Cuadrado, J.S, Molin, J.S, Approaches for Model Transformation Reuse: Factorization

and Composition. ICMT’2008, Pages 168-182.

11. Roser, S., Bauer, B, Automatic Generation and Evolution of Model Transformations Using

Ontology Engineering Space, Journal on Data Semantics XI, 2008

12. Almeida, A.J.P., 2006. Model-driven design of distributed applications. PhD thesis,

University of Twente. ISBN 90-75176-422.

13. Sendall, S., Kozaczynski, W. 2003. Model Transformation – the Heart and Soul of Model

Driven Software Development. IEEE Software, Special Issue on Model Driven Software

Development, pp42-45, Sept /Oct 2003.

14. Kleppe, A., Warmer, J., Bast, W., 2003. MDA Explained: The Model Driven Architecture:

Practice and Promise. Addison-Wesley, 1st edition.

15. Feiyu, L. State of the Art: Automatic Ontology Matching, Research Report, School Of

Engineering, Jonkoping, Sweden, 2007.

16. Lopes, D., Hammoudi, S., De Souza, J., Bontempo, A., 2006. Metamodel matching:

Experiments and comparison. In ICSEA'06, Proceedings of the International Conference on

Software Engineering Advances.

17. Del Fabro, M. D., 2007. Semi-automatic Model Integration using matching transformation

and weaving models. In SAC’07, ACM.

18. Kappel, G., Kargl, H., Kramler, G., Schauerhuber, A., Seidel, M., Strommer, M., Wimmer,

M., 2007. Matching Metamodels with Semantic Systems – An Experience Report. In BTW

2007, Datenbanksysteme in Business, Technologie and Web.

19. Kurtev, J. Bézivin, and M. Aksit. Technological spaces: An initial appraisal. In Int.

Federated Conf. (DOA,ODBASE, CoopIS), Industrial track, Los Angeles, (2002)

20. Melnik, S. , Garcia-Molina, H. Rahm, E. Similarity Flooding: A Versatile Graph

Matching Algorithm and Its Application to Schema Matching. In Proceedings of the 18th

international Conference on Data Engineering (February 26-2002). ICDE. IEEE Computer

Society, Washington, Pages 117-128.

21. Falleri, J.R. , Huchard, M. Lafourcade, M. Nebut, C. Metamodel matching for automatic

model transformation generation. In: Proceedings of MoDELS ’08, (2008) 326–340.

22. Jose de Sousa Jr, Denivaldo lopes, Daniela Barreiro Claro, and Zair Abdelouahab. A Step

Forward in Semi-automatic Metamodel Matching: Algorithms and Tool.

23. Bernstein, P.A, 2003. Applying Model Management to Classical Meta Data Problems. In

CIDR’03, Proceedings of the Conference on Innovative Data Systems Research. CIDR.

24. Chukmol, U., Rifaiem, R., Benharkat, N.: EXSMAL: EDI/XML Semi-Automatic Schema

Matching ALgorithm, Proceedings of the Seventh IEEE International Conference on

ECommerce Technology, IEEE Computer Society, 422-425, (2005)