Experiments with Single-class Support Vector Data

Descriptions as a Tool for Vocabulary Grounding

Aneesh Chauhan

and Luís Seabra Lopes

1,2

Actividade Transversal em Robótica Inteligente

IEETA

/DETI

, Universidade de Aveiro, 3810-193 Aveiro, Portugal

Abstract. This paper explores support vectors as a tool for vocabulary

acquisition in robots. The intention is to investigate the language grounding

process at the single-word stage. A social language grounding scenario is

designed, where a robotic agent is taught the names of the objects by a human

instructor. The agent grounds the names of these objects by associating them

with their respective sensor-based category descriptions. A system for

grounding vocabulary should be incremental, adaptive and support gradual

evolution. A novel learning model based on single-class support vector data

descriptions (SVDD), which conforms to these requirements, is presented. For

robustness and flexibility, a kernel based implementation of support vectors

was realized. For this purpose, a sigmoid kernel using histogram pyramid

matching has been developed. The support vectors are trained based on an

original approach using genetic algorithms. The model is tested over a series of

semi-automated experiments and the results are reported.

1 Introduction

The meanings of words lie in concomitance with the entities of the world they refer to

(Barsalou 1999; Harnad 1990). Supported by the studies carried out on populations of

robots – to study origins, evolution and transfer of language – a new view is emerging

that considers language a cultural product (Love 2004; Roy and Pentland 2002;

Seabra Lopes and Chauhan 2007, 2008; Steels and Kaplan 2002). Here the language

grounding process is considered distributed in nature, where the language symbols are

acquired (and transferred) through social interactions (Cowley 2007; Loreto and

Steels 2008; Steels 2007). It can be inferred from this argument that there are two key

factors that influence language acquisition. On the one hand, language is acquired

through social interactions, leading to a set of shared language symbols. On the other

hand, the meaning formation of these symbols is an internal cognitive task, where the

symbols refer to the real world entities.

In the past decade, a significant amount of work has been carried out on designing

robotic agents that acquire their vocabulary through social interactions with humans.

Many approaches have been designed that use humans to teach robots the names of

visual concepts. This paper discusses a similar approach, where a robotic agent

acquires its vocabulary through interaction with a human instructor. The agent is

embodied with a camera for visual perception and grounds the words taught by the

Chauhan A. and Lopes L.

Experiments with Single-class Support Vector Data Descriptions as a Tool for Vocabulary Grounding.

DOI: 10.5220/0003028000700078

In Proceedings of the 7th International Workshop on Natural Language Processing and Cognitive Science (ICEIS 2010), page

ISBN: 978-989-8425-13-3

instructor in their respective visual descriptions.

Similar works have been reported in literature where these approaches differ from

each other based on the choice of methods for learning visual concepts. Gold et al

(2009) explore an approach based on dynamic decision trees; Levinson et al (2005)

investigate Hidden Markov Models for the similar purpose; Roy and Pentland (2002)

used neural networks and density match in their CELL model; Seabra Lopes and

Chauhan (2007) used support vector data description (SVDD) (Tax 2001) based

approach and later investigated multiple other classifiers and classifier combinations

(2008); and Skocaj et al (2007) use the single most suitable prototype to describe a

visual concept. The number of words learned in these approaches ranges between 3

and several tens of categories.

The learning algorithm for this work is SVDD. The motivation behind this

preference is to imitate the language development process in children at the single-

word stage. Studies in cognitive language development literature indicate that

children predominantly learn from positive examples only (Bloom, 2000; Markman,

1989). A learning methodology to imitate child like word grounding should support

similar process. SVDD is a single-class classifier that has been shown to be robust at

novelty detection tasks using only a few positive examples (Tavakkoli et al 2008; Tax

2001). However, in its original form SVDD is neither incremental, nor can it handle a

multitude of outliers, making it unsuitable for the open-ended processes like

vocabulary acquisition.

In this paper, a novel strategy is presented where the SVDD optimization process

has been modified so as to make it more efficient for incremental, online and open-

ended processes. A new method based on a genetic approach has been designed for

optimizing various magic parameters of the SVDD. The genetic approach for

optimizing parameters has previously been shown to improve the SVDD performance

(Tavakkoli et al 2008). But the approach of Tavakkoli was not incremental.

Incremental learning brings different challenges and the approach in this paper has

been specifically designed for such learning processes.

The rest of the paper is organized as follows. Next section describes the approach

for social language transfer between the robot and its instructor. Section 3 details the

learning and categorization methodology. Section 4 reports and discusses the

experiments and the final section concludes the paper.

2 Interaction Approach for Social Language Transfer

Any two individuals (robots or humans) can share a language if they ground the same

words to the same entities, regardless of their respective process of meaning

formation. With this in mind, a social language scenario is designed where a human

instructor teaches the robotic agent the names of the objects present in their visually

shared environment.

The robotic agent is embodied with a camera to visually perceive its world.

This camera is mounted over a table which becomes a shared environment between a

human instructor and the robot. The names taught by the instructor are grounded by

the robotic agent in visual descriptions, leading to a vocabulary shared with its

instructor.

Fig. 1. Robot’s visual scene and an extracted object as selected by the user.

The instructor selects (by mouse-clicking on the visual scene) an object from the

robot’s visible scene (Fig.1). The selected object is extracted from the visual scene

and further processed to compute a set of shape features. The shape of the object in

this implementation is expressed using the vector of normalized-radii features

(described in Seabra Lopes and Chauhan 2007). This feature vector has previously

been shown to be a robust shape descriptor and faithfully captures the shape of a

segmented object, invariant to size, translation and rotation. Once the object has been

extracted from the scene, the instructor can interact with the robot through the

following instructions (using a menu-based interface):

1. Teach the category name of the selected object;

2. Ask the category name of the selected object;

3. If the category predicted in the previous case is wrong, send a correction.

4. Provide a category name and ask the robot to locate an instance of that category;

5. If the object identified by the robot in the previous case does not belong to the

requested category, provide the true category.

The robot can respond to the human instructions in either of the following ways:

1. Linguistic response: provide the classification results to the user;

2. Visual response: visually report the results of a “search/locate” task.

Simulated Instructor Agent. Teaching vocabulary to the robotic agent can be an

extremely exhaustive task for the human user. Therefore, a simulated user has been

developed for the purposes of the experiments reported in this paper. The actions of

this agent are limited to the following actions of the human user: teaching, asking and

correction.

From many previous experiments a database of ~7000 images (from 69 categories)

has been collected. The extracted object in Fig. 1 can give an idea of the type of

images in this database. Most of these images (and their category names) were

collected during a long duration experiment, where a human user followed a teaching

protocol to teach the category names to the robotic agent (Seabra Lopes and Chauhan

2008).

3 Learning and Categorization

This paper presents a novel methodology for category learning and classification

based on the single-class SVDD (Tax 2001). For a given set X of positive examples,

the SVDD approach tries to locate the data points x

(i.e. the support vectors) that

form a closed description around the data. In a regular case, this approach will give a

closed spherical description around all the data points. Tax showed that by mapping

the data points to a better feature space (by applying a kernel function K on the data),

a much more robust and flexible data description can be achieved. Such a description

is referred as a hypersphere. The optimization process used to determine the center

and the support vectors attempts to minimize two errors: Empirical error – percentage

of misclassified training samples; Structural error – radius R

of the hypersphere

which must be minimized with respect to the center a with certain constraints. Tax

gives the final error L to be minimized as:

iij

L α K(x ,x )=

∑

–

ij i j

i, j

αα K(x ,x )

∑

(1)

with the following constraints on the Lagrange multipliers α

∀

10 ≤≤

α ; 0≥

α , 1

α =

∑

; and

a= α x

∑

(2)

Minimization of L with these constrains is a classic quadratic optimization

problem. To find optimal support vectors many optimization approaches have been

developed (e.g. SMO (Platt 1998) and the genetic approach of (Tavakkoli et al

2008)). For the SVDD, the genetic approach of Tavakkoli et al led to a more robust

and efficient optimization in comparison to other methods. However, their approach

was neither incremental nor online. For an open-ended domain like vocabulary

acquisition, a learning process needs to be incremental, online and open-ended. Such

process requires continual assessment and updates of the support vectors when the

new data gets introduced. The SVDD parameter optimization used in this paper is

also based on using genetic algorithms, but the methodology has been designed to

take the open-ended nature of vocabulary learning into account.

An instance based approach has been used for category representations, where a

category is described by a set of known instances belonging to that category. An

instance is added to a category description when an instructor teaches the name of a

selected instance (teaching actions) or provides a correction in case of an incorrect

prediction by the robot (correction action). Each time a new instance is added to a

category description a new chromosome is created with as many genes as the number

of instances in the description. A new gene is also added to the existing

chromosomes. These new genes contain a randomly chosen value of α

and all the

existing genes are modified to be in the range listed in equation (2). In this

implementation, the number of chromosomes is limited to 20, while there is no limit

on the number of genes added. At any certain moment in time, the best chromosome

for a category description is used as its Lagrange multipliers. Before describing the

Lagrange parameter optimization, both the kernel function and the classification

methodology have to be elaborated.

Although the choice of kernel is data dependent, in most applications the Gaussian

kernel produces good results (Tax 2001). This is also the choice for the experiments

reported here. The kernel K used in this paper is defined as:

),(

xxK

exp

Ni j

( P (x ,x ))

−−

⎛⎞

⎜⎟

⎝⎠

(3)

where x

and x

are the i

and j

instances describing a category; σ is the standard

deviation of the data; and P

) is the normalized pyramid match and is given as

P(x

)/Max_Match, where P(x

) is the pyramid match (Grauman and Darrel 2007)

found on the feature vectors x

,and x

. The highest value (Max_Match) that a pyramid

match can achieve on any two sets of equal sized features is the number of elements

contained in a feature vector (in our case 40).

Given an instance z to be classified, Tax (2001) describes its membership to a

category C with the hypersphere radius R

(,) ( ())

DCz R C<

(4)

where, D(C,z) = 1+

(, )2 (,)

ij i j i i

ij i

xx Kzx

αα α

−

∑∑

D(C,z) is the distance of the input instance z from the hypersphere center. If the

distance is less than the squared radius of a category description, the instance is

considered to belong to that category. To accommodate multiple category

descriptions, the distance of instance z from the hypersphere boundary is calculated

and the category description giving lowest boundary distance is predicted as the

category of that instance. This boundary distance is given as:

(C,z) = (R

(C))

- D(C,z)

(5)

// C

is the input category description

n = 1;

//Chromosome index

repeat {

i = 1; //Category index

fitness(cr

) = 0;

repeat {

= randomly chosen instance from C

;

= randomly chosen instance from C

;

if (C

== C

) continue;

// Test whether using cr

interferes with the recognition capacity

// of existing categories

if (B

, x

) > B

, x

)) // No interference

fitness(cr

) ← fitness(cr

) + 0.5;

else fitness(cr

) ← fitness(cr

) - 0.5;

// Test whether using cr

improves the recognition capacity of

// instances belonging to C

if (B

, x

) > B

, x

)) // Correct recognition

fitness(cr

) ← fitness(cr

) + 0.5;

else fitness(cr

) ← fitness(cr

) - 0.5;

i ← i + 1;

} until (i > number of categories)

fitness(cr

) ← fitness(cr

) / (total number of categories – 1);

n ← n + 1;

} until (fitness(cr

) > 95% OR all chromosomes have been evaluated)

___________________________________________________________________________

Fig. 2.

The core function to evaluate the fitness of a chromosome.

Fig. 3. The possible crossover and mutation capabilities of the system (the constraints

mentioned in equation (2) are always maintained). Similar operations are carried out to

optimize σ values.

Given a category description, the optimization process attempts to iteratively

evolve the set of chromosomes until the best chromosome has been found, without

affecting the boundary descriptions of other category descriptions. In the current

implementation the number of iterations used was 300 (usually the best solution was

reached much earlier). Fig.2 describes the function designed to evaluate the fitness of

the chromosomes for a given category. This function is called for each of the

iterations. If no chromosome reached the desired fitness (85%) in a particular

iteration, all the chromosomes are randomly mutated or crossed over (see the

illustration in Fig.3).

The key advantage of this strategy is that the optimization procedure, instead of

minimizing the error L (equation (1)), tries to find the best set of Lagrange multipliers

using the classification success of each chromosome while trying to maintain the

classification performance over existing category descriptions. This makes the

optimization process feasible for incremental, online, open-ended and multiple

category scenarios.

4 Experimental Evaluation

Experiments were conducted to evaluate the performance of the new learning system

on vocabulary acquisition using an experimental protocol. This protocol (“teaching

protocol” (Seabra Lopes and Chauhan 2007)) is generic enough to be applied to any

incremental and open-ended class learning domain. An instructor, following this

protocol, performs either “teach”, “ask” or “correct” actions. As the protocol

progresses, the robot accumulates new words. The protocol dictates that, at the

introduction of a new category, the recognition performance over the previously

learned categories should be tested and the next category should be introduced only

when the performance of the overall learning system is above a set threshold (66.67%

for reported experiments). The classification precision measure (computed over a

fixed number of most recent question-correction iterations) is used to analyze the

impact of a new category on the learning system, from initial instability to final

recovery in system's performance. An experiment is concluded when the robot is

unable to recover from the initial instability at the introduction of a new class (i.e.

when the breakpoint is reached). One more evaluation measure – overall system

precision, calculated as an average over all the classification precision values for all

the question-correction iterations - has been used to evaluate the overall performance

of the system.

Table 1. Summary of experiments.

Exp #

# cats at

breakpoint

# Question

/correction

iterations

Class.

precision at

breakpoint

(%)

# Avg.

instances

per category

at breakpoint

System precision

before the

introduction of the

last category

(%)

1 33 1519 62 17.8 71

2 20 1036 60 20.8 63

3 29 1349 58 18.6 70

4 29 1621 60 22 66

5 27 1246 53 18.3 65

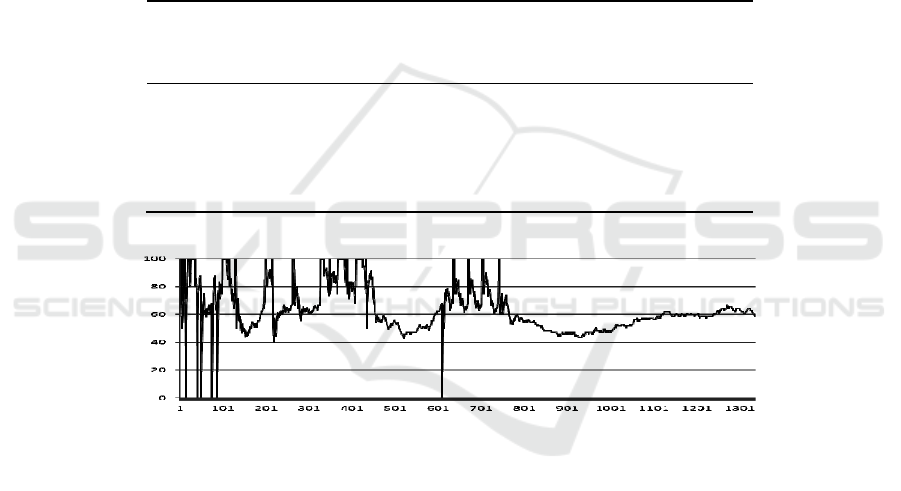
Fig. 4. Evolution of classification precision versus number of question/correction interactions

in the third experiment.

Experiments were conducted using the simulated instructor agent. For each

new/learned category, the instructor randomly selects an instance of that category

from the image database, preserving the essence of natural interactions. When all the

images of particular category have been used or if all the categories in the database

have been exhausted, the human user is called to show a new image or to introduce a

new category.

In total 5 experiments were conducted, where the robot was able to learn

somewhere between 19-32 categories. Table 1 provides a summary of these

experiments when the breakpoint was reached. The last column of Table 1 gives the

overall system precision over the question/correction iterations right before the final

category was introduced. Thus the system precision is used here to show the

performance of the learning methodology over the set of categories that were

successfully learned.

Fig.4 illustrates the evolution of classification precision in the third experiment. In

this experiment, the robot learned 28 categories (and category names). In general, the

introduction of a new category to the agent led to the deterioration in classification

precision followed by gradual recovery. Each such introduction can affect the

classification performance over other categories, since any new data can lead to the

confusion between different boundary descriptions. The depressions in the graph

normally indicate the period after the introduction of a new category. At each

misclassification on any learned category, the optimization process is carried out to

derive the fittest chromosome. This leads to a gradual system recovery, eventually

improving the complete system performance. This process continues until the system

starts to confuse the category descriptions to an extent that it can no longer recover.

For an example, on the introduction of 29

category in experiment 3, the precision

remained around 57% (for ~500 iterations) without showing signs of recovery. All the

reported experiments showed similar classification precision evolution pattern.

5 Conclusions

This paper presented a novel approach to grounding vocabulary in robotic systems.

This approach is inspired by the studies on grounding vocabulary through social

interactions. A scenario has been designed where a human instructor can teach the

robot the names of objects present in their visual environment. The robot grounds

these words in its visual-sensor based descriptions.

The key contribution of this paper has been the use of single-class SVDD for

vocabulary learning. The SVDD has been modified so as to be able to function in

incremental, online, open-ended and multiple category scenarios. A novel genetic

approach has been designed that modifies the optimization criteria of the SVDD.

Instead of considering the optimization of Lagrange parameters as a quadratic

optimization problem, the new approach tries to optimize these multipliers based on

the classification success of a category on its own instances. The fitness function has

been designed to maximize self categorization, without affecting the existing category

descriptions.

The robot was able to incrementally learn between 19 and 32 categories in 5

different experiments. The evolution process of the classification precision in

different experiments clearly shows that the proposed strategy is capable of

incremental learning in open-ended scenarios. On the other hand, the number of

categories learned was very limited. We believe, however, that the approach is

promising. There are perhaps many areas where improvements can be made. But the

fitness strategy itself will be the key to better performance. Future work will primarily

entail refining the optimization process by investigating more robust fitness functions,

while maintaining the optimization criteria.

References

1. Barsalou, L. 1999. Perceptual symbol systems. Behavioral and Brain Sciences, 22(4):

577–609.

Bloom, P. 2000. How Children Learn the Meanings of Words. MIT Press, Cambridge, MA.

Cowley, S. J. 2007. Distributed language: Biomechanics, functions and the origins of talk.

In Lyon, Nehaniv & Cangelosi (eds), Emergence of communication and language, 105-127.

Gold, K.; Doniec, M.; Christopher, C.; and Scassellati, B. 2009. Robotic Vocabulary

Building Using Extension Inference and Implicit Contrast. Artificial Intelligence

173(1):145-166.

Harnad, S. 1990. The symbol grounding problem. Physica D, 42:335-346.

Grauman, K.; and Darrell, T. 2007:The Pyramid Match Kernel: Efficient Learning with

Sets of Features. Journal of Machine Learning Research (JMLR), 8 (Apr): 725-760.

Levinson, S. E.; Squire, K.; Lin, R. S.; and McClain, M. 2005. Automatic language

acquisition by an autonomous robot, Proc. of AAAI Spring Symposium on Developmental

Robotics.

Loreto, V.; and Steels, L. 2008. Social dynamics: Emergence of language. Nature Physics,

3:758-760

Love, N. 2004. Cognition and the language myth. Language Sciences, 26:525-544.

10.

Markman, E.S. (1989) Categorization and naming in children. Cambridge, MA: MIT Press.

11.

Platt, J. 1998. Sequential minimal optimization: A fast algorithm for training support vector

machines. Microsoft Research Technical Report MSR-TR-98-14.

12.

Roy, D.; and Pentland, A. 2002. Learning words from sights and sounds: A computational

model. Cognitive Science, 26:113-146.

13.

Seabra Lopes, L.; and Chauhan, A. 2007. How many Words can my Robot learn? An

Approach and Experiments with One-Class Learning. Interaction Studies, 8(1):53-81.

14.

Seabra Lopes, L.; and Chauhan, A. 2008. Open-ended category learning for language

acquisition. Connection Science, 20(4):277-297.

15.

Skocaj, D.; Berginc, G.; Ridge, B.; Štimec, B.; Jogan, M.; Vanek, O.; Leonardis, A.;

Hutter, M.; and Hewes, N. 2007. A system for continuous learning of visual concepts,” In

International Conference on Computer Vision Systems ICVS 2007, Bielefeld, Germany.

16.

Steels, L. 2007. The symbol grounding problem is solved, so what's next? In De Vega, M.

and G. Glennberg and G. Graesser (eds), Symbols, embodiment and meaning. Academic

Press, New Haven.

17.

Steels, L.; and Kaplan, F. 2002. AIBO’s first words: The social learning of language and

meaning. Evolution of Communication, 4(1):3-32.

18.

Tavakkoli, A.; Nicolescu, M.; Bebis, G.; and Nicolescu, M. 2008. A support vector data

description approach for background modeling in videos with quasi-stationary

backgrounds", International Journal of Artificial Intelligence Tools, 17(4):635-658.

19.

Tax, D. M. J. 2001. One Class Classification. PhD Thesis, Delft University of Technology