VEHICLE ROUTING TO MINIMIZE MIXED-FLEET FUEL

CONSUMPTION AND ENVIRONMENTAL IMPACT

O. Gusikhin

, P. MacNeille

and A. Cohn

Ford Motor Company Research and Innovation Center, 2101 Village Road, Dearborn, MI 48121, U.S.A.

University of Michigan, 2797 IOE Building, 1205 Beal Avenue, Ann Arbor, MI 48019, U.S.A.

Keywords: Fuel Economy, Heterogeneous Vehicle Routing Problem, Optimization.

Abstract: Efficient vehicle routing is critical to the operational profitability and customer satisfaction of vehicle fleet-

related businesses, especially in light of increasing, and highly volatile, fuel prices. Growing pressures to

reduce negative environmental impacts have suggested that a second metric (vehicle emissions) should also

be considered in vehicle routing. Currently, the majority of existing tools use distance as a surrogate for

cost. When considering a mixed fleet of multiple vehicle types, with individual vehicles within a fleet type

also varying by age and vehicle health, this surrogate becomes significantly less accurate. Furthermore,

using distance as a surrogate fails to capture the variations between city and highway driving, which are

particularly striking for hybrid vehicles. We thus propose a new approach to the vehicle routing problem,

specifically targeting applications with mixed fleets including clean-vehicle technologies, in recognition of

the limitations of the existing approaches.

1 INTRODUCTION

Efficient vehicle routing is critical to the operational

profitability and customer satisfaction of vehicle

fleet-related businesses. The rising and highly-

variable cost of fuel, as highlighted by the price

spike in the summer of 2008, increases the

importance of efficient vehicle routing. At the same

time, growing environmental concerns suggest that

cost is not the only metric of importance and that

emissions should also be taken into account.

Currently, the majority of existing methods and

software packages minimize travel distance as a

surrogate for cost. Although there is a positive

correlation between distance traveled and fuel

consumed, it is not a perfect correlation. In

particular, both fuel efficiency and emissions vary

depending upon driving conditions (e.g. city vs.

highway driving). This variability is even more

pronounced in a heterogeneous fleet comprised of

multiple vehicle types with a range of fuel-

consumption and emissions characteristics.

In recent years, socio-economical pressures to

reduce their fuel costs and carbon dioxide (CO

)

footprint have motivated many fleet operators to

begin upgrading their fleets, focusing on clean-

vehicle technologies and alternative fuels, including

flex-fuel, hybrid vehicles, and plug-in hybrid electric

vehicles (PHEV). As a result, many commercial

fleets are currently composed of a heterogeneous set

of vehicles, with noticeable variations in fuel

economy and emissions across vehicle type.

Furthermore, there are variations across vehicles

even within a given vehicle type or common set of

capabilities, because newer vehicles typically exhibit

better fuel economy and better emission control

technologies than older vehicles.

Consider the following examples of highly

heterogeneous fleets: Florida Power and Lighting

(www.fpl.com), the leader in green fleet initiatives,

has a fleet of approximately 2400 vehicles, with half

of the fleet powered by biodiesel, 300 hybrids and

plug-in hybrids now in service, and plans to convert

one-third of the vehicles to hybrid by the end of

2010.

A key issue in incorporating the fuel efficiencies

and emissions of heterogeneous fleets within the

vehicle routing problem is this: The differences in

fuel efficiencies and emissions across vehicle types

are not exclusively proportional to the distance

traveled, but are also highly dependant on the

driving cycle. For instance, a hybrid vehicle takes

advantage of the regenerative braking that occurs in

stop-and-go driving environments to charge a

battery which can then be used to power the vehicle

285

Gusikhin O., MacNeille P. and Cohn A. (2010).

VEHICLE ROUTING TO MINIMIZE MIXED-FLEET FUEL CONSUMPTION AND ENVIRONMENTAL IMPACT.

In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 285-291

 SciTePress

when traveling at slow speeds. On average, fuel

consumption is reduced about 20% by regenerative

braking (Chan and Chau, 2001). Conversely, in

highway driving, hybrids provide minimal, if any,

improvement in fuel efficiencies over their

conventional counterparts.

The introduction of PHEVs, which use

electrically-charged batteries for the initial portion

of a trip and revert to gasoline-based power only

when the battery has been depleted, presents even

greater variability in terms of the correlations

between distance and fuel utilization.

When we move beyond fuel costs to also

consider the environmental impact of vehicle

routing, the complexity grows further. Fuel

consumption is effectively proportional to CO

emission, so fuel economy improvements are

reflected in CO

reduction. Additionally, there may

be requirements to minimize or eliminate

conventional emissions such as volatile organic

components (VOC) and nitrogen oxides (NO

)

emissions in highly populated areas, requiring the

use of electric power or other clean alternative fuel

options and thus limiting the feasible region of a

vehicle routing problem.

In this paper, we consider ways to explicitly

capture fuel consumption and emissions in a mixed-

fleet vehicle routing program and analyze the

opportunities for simultaneously reducing costs and

negative environmental impacts. In Section 2, we

review factors that influence fuel consumption and

emissions and consider ways to estimate these

metrics for a given route. In Section 3, we suggest a

number of formulations for this new variation of the

vehicle routing problem. We also outline a solution

approach based on composite variable modeling. In

Section 4, we provide a numerical example and

analysis to highlight the benefits of our proposed

approach and we then offer conclusions and

suggested areas for future research in Section 5.

2 ESTIMATION OF FUEL

ECONOMY & VEHICLE

ENVIRONMENTAL IMPACT

Route planning is done by representing the road

system as a graph in which intersections are nodes

and road segments are arcs. To determine the best

route from an origin node to a destination node, each

arc is associated with a cost that represents distance,

travel time, or fuel consumption. Then Dijkstra's

algorithm (or an equivalent) is used to find the

lowest cost path which is then inversed mapped to

the road system for visualization and navigation of

the preferred route.

Total fuel cost along a given route is the product

of the total consumption of each type of fuel and the

per-unit cost for that fuel. Total fuel consumption

along an arc is largely dependant on the vehicle

specific load (VSL) opposing vehicle motion

multiplied by the distance traveled against the VSL

to give the total energy required to travel the arc.

This energy can be readily converted into fuel. For

example, about 0.003 gallons of gasoline or 0.002

kWh of electricity are needed to push against a

pound of force over a one mile stretch of road. These

factors will vary, however; with the efficiency of the

energy conversion which depends on many factors.

The VSL depends largely on external factors that

include the drive cycle, aerodynamic drag, rolling

resistance, parasitic drag, and gradient drag. These

factors in turn are dependant on several external

factors including weather conditions, road and traffic

conditions and topography. Most of the external

factors can be reasonably well estimated using well

known engineering formulas; however, the VSL also

depends on the pattern of acceleration/deceleration

that takes place along the branch. Driving pattern

effects depend largely on complex interactions

between the driver, the road, the powertrain, and

traffic conditions. Thus, these effects are difficult to

predict.

One approach to predicting these complex

factors is by classifying road, traffic, and driver and

drivetrain combinations into load effects. The US

Environment Protection Agency (EPA) provides

miles per gallon estimates for highway and city for

all vehicles sold in the US in the last 15 years

currently based on two standard driving cycles.

Although these estimates may not be adequate to

accurately forecast the specific fuel consumption,

they nevertheless can provide a reasonable basis for

the comparative analysis between different vehicles.

A more detailed classification is described in

Brundell-Freij and Ericsson (Brundell-Freij and

Ericsson, 2005), where a classification system has

been developed based on extensive data collected

from instrumented vehicles. Four variables relating

to the road type were found to be significant: 1)

occurrence and density of junctions controlled by

traffic lights, 2) speed limit, 3) function of the street,

and 4) the type of neighborhood. A large effect was

attributed to the power-weight ratio of the vehicle,

which presumably is descriptive of the drivers that

choose a vehicle with a specific power-weight ratio.

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

286

A challenge in using instrumented vehicles is in the

ability to collect adequate data. For example, in the

Brundell-Freij and Ericsson study much of the data

was collected in Lund, Sweden. This location has

limited topography, so road gradient was not

captured, although it is well known that road

gradient is an important factor in situations with

topographic relief. For example, (Tavares et al.,

2009) develops a topography-based routing

algorithm for waste collection vehicles in a

mountainous area and demonstrates that the

proposed approach allows reduction of fuel

consumption despite increasing in the distance

traveled. Also road design and traffic control

policies may vary considerably between political

jurisdictions, as may the mix of vehicles. One way to

overcome these difficulties is to use vehicle and

traffic modeling to determine the significant factors

for classification.

Modeling tools such as the Powertrain System

Analysis Toolkit (PSAT) (PSAT, 2008) or The

MathWorks Simulink/SimDriveLine (Rose-Hulman,

2005) can be used to estimate the energy or fuel

along a route given vehicle design parameters,

external load factors such as road gradient and the

driver's torque demand along the route. Vehicle

design parameters can be obtained from vehicle

manufacturers and external factors from published

maps. Driver's torque demand involves the

psychophysics of driving and has been simulated

using software such as VISSIM

or MISSION (PTV

AG, 2009), (Wiedemannn et al., 1991), (Busawon et

al., 2006), (Noland and Quddus, 2006).

Vehicles in the fleet may be instrumented to

collect actual fuel economy data along the branches

they travel. The data may be recovered from the

vehicle at a download site and stored in a database.

Periodically the database may be used to

automatically refine the costs assigned to a class of

road segments, and to reclassify segments as needed.

3 VEHICLE ROUTING TO

MINIMIZE FUEL

CONSUMPTION

The Vehicle Routing Problem to Minimize Mixed-

Fleet Fuel Consumption and Environmental Impact

(VRPMF) belongs to the class of heterogeneous fleet

vehicle routing problems (HVRP). (Baldacci et al.,

2008) provides a comprehensive classification and

review of the main approaches proposed for VRP

with a heterogeneous fleet. Specifically, the problem

being considered in the paper represents a variant of

HVRP with Vehicle-Dependent Routing Costs

(HVRPD). They note that solution approaches to

this difficult family of problems, both in the

literature and in commercial applications, have

predominantly been heuristic in nature. These are

typically adaptations or extensions of solution

techniques for traditional VRP and VRP with Time

Windows.

In order to capture the complexities (and, in

particular, the non-linearities) of VRPMF, we

instead propose to leverage the use of composite

variable modeling (CVM) to capture the complex

real-world details associated with accurately

modeling the fuel cost (and associated emissions) of

a prescribed route. The idea behind CVM (Cohn,

2002), (Barlatt, et al., 2009) is to embed modeling

complexity into the variable definition rather than

capturing it explicitly in a model which may then

become intractable. For example, in VRPMF,

explicitly modeling the cost functions described in

Section 2 within the framework of a traditional VRP

would make an already difficult problem unsolvable.

However, it is far easier to calculate the cost of a

given route (for a given vehicle) off-line. We can

then formulate a master problem in which each

variable represents the assignment of a specific route

to a specific vehicle. For a given route, we can

compute the total fuel consumption for a given

vehicle, and thus the total cost is just the sum of the

chosen assignments. Similarly, a route pre-specifies

all the customer demands that it meets, and thus we

only need two sets of constraints. The first ensures

that each vehicle is assigned to at most route and the

second ensures that each customer demand is met

exactly once.

The challenge, then, is to address the

exponentially large number of potential variables.

Clearly not all of the exponentially-large set of

feasible routes (and their corresponding costs) can

be generated. Even if they could, it would not be

possible to solve the resulting exponentially-large

set partitioning problem. Instead, column generation

techniques (Desaulniers et al., 2005) (originally

developed as part of Dantzig-Wolfe Decomposition)

can be employed. The idea behind column

generation for solving a linear program with an

exponential number of variables is to identify

candidate pivot variables for the simplex method not

by pricing each variable’s reduced cost directly, but

rather by solving a secondary optimization problem

(often called a sub problem) which seeks the feasible

variable with the most negative reduced cost. If this

yields a negative reduced cost variable, then the

VEHICLE ROUTING TO MINIMIZE MIXED-FLEET FUEL CONSUMPTION AND ENVIRONMENTAL IMPACT

287

simplex pivot occurs and the algorithm proceeds. If

the most negative reduced cost variable is strictly

non-negative, then a certificate of optimality is

achieved and the algorithm terminates with a

provably-optimal solution.

In Dantzig-Wolfe Decomposition, the inherent

structure of a problem leads to a sub-problem that is

pre-defined. Furthermore, it is itself a linear program

and thus straightforward to solve. In CVM, because

the variable definition is chosen specifically to

overcome challenges of a traditional formulation, the

sub problem reflects these challenges.

Perhaps the most closely related work to our

proposed approach is that of Taillard (Taillard,

2005), who used a heuristic based on column

generation techniques to solve HVRPD.

Specifically, a large set of candidate routes were

generated by solving separate homogeneous VRP

problems for each fleet type. The final routes were

then selected using a set partitioning formulation to

ensure that all demands were met.

A key difference between our proposed approach

and typical network-based routing problems is that

the “cost” of a route cannot be computed simply by

adding the individual arc costs (if so, the sub-

problem would be a simple minimum cost flow

problem). At first glance, it seems possible to

formulate the sub problem as a network flow

problem, where each node represents a customer or

depot, each arc represents the driving from one node

to another, and the cost associated with each arc can

fully capture (based on off-line calculations) the cost

of this driving. This is not quite true, however: The

cost on a given arc is not independent of the other

arcs that are also chosen for an individual vehicle’s

route. This is because the fuel consumption on an

arc depends on the starting conditions of the vehicle

at the first node. If the battery is fully charged, it

may be possible to complete most of the driving

without relying on gasoline, and the resulting cost

will be lower, whereas if the battery is depleted, the

cost of the arc will be much higher.

Therefore, a more sophisticated approach to

solving the sub-problem must be employed. For

example, we could take a multi-label shortest path

approach (Desrochers and Soumis, 1988), which is

similar to Dijkstra’s shortest path algorithm, but

with an added layer of complexity. Specifically,

multiple metrics (not just cost) must be checked to

determine whether a partial path can be pruned from

consideration. One partial path dominates another

only if it is less costly and covers the same amount

of demand or more and has the same amount of

remaining battery charge or more. Efficiently

solving this sub-problem is the key to successfully

solving the master problem.

We conclude this section by noting that this

approach has the added advantage of allowing the

user to trade off between time and solution quality.

Specifically, the solution quality continues to

improve as each new candidate route is added to the

master problem for consideration, but high-quality

feasible solutions can nonetheless often be found

early in the process. Furthermore, this approach

naturally lends itself to a parallel implementation. At

the highest level, a separate sub-problem can be

solved, in parallel, for each vehicle. Furthermore,

these individual sub-problems themselves can

leverage a parallel architecture for efficient search.

4 ILLUSTRATIVE EXAMPLE

This section provides a simplified illustrative

example of VRPMF. We consider a fleet of two

vehicles: the first is a 2009 Ford Taurus front-wheel

drive gasoline engine vehicle and the second is 2010

Ford Escape 4-wheel drive hybrid vehicle. Figure 1

shows estimates of the miles per gallon (MPG)

values and environmental scores as provided by the

US Environmental Protection Agency (EPA) at

www.fueleconomy.gov. Note that the Taurus gets 18

MPG in city driving and 28 MPG in highway

driving, while the Escape hybrid gets 27 MPG on

the highway and 30 MPG in the city. The

environmental impact of each vehicle can be

evaluated by its carbon footprint and air pollution

score. The carbon footprint measures greenhouse gas

emissions (primarily CO

) that in turn impact

climate change. CO

emissions are closely linked to

fuel consumption, since CO

is the ultimate end

product of burning gasoline. The Air Pollution score

represents the amount of health-damaging and

smog-forming airborne pollutants (such as carbon

monoxide, CO, and oxides of nitrogen, NOx) that

the vehicle emits on a scale from 0 (worst) to 10

(best). Note that there is little correlation between

fuel consumption and these emissions; emissions

primarily depend on the emission control

technology. Taurus has an Air Pollution score of 6

and Escape Hybrid has a score of 8.

Suppose that we have eight customers distributed

within a given geographical area as shown in Figure

2. The customers are labeled 1 to 8, while 0 is the

depot. The driving distance between the depot and

each of the customer sites is presented in Table 1.

For this example, we assume that the distance data is

symmetrical and shown as X+Y, where X is the

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

288

Table 1: Distance between depot and between customer's sites.

012 3456 78

14.5+ .9 19+ 1 23.9+ 2.4 0+ 11.6 0+ 9.8 0+ 13.6 12.5+ 10 15.5+ 1.1

14.5+ .9 4.2+ 1.5 10.2+ 1.8 0+ 6.3 0+ 10.3 0+ 12.1 12.2+ 2.6 0+ 17.9

19+ 1 4.2+ 1.5 5.7+ 2.2 2.5+ 9.1 4.2+ 11.6 11.4+ 4.7 7.7+ 2.9 20.2+ 2

23.9+ 2.4 10.2+ 1.8 5.7+ 2.2 0+ 6.7 0+ 10.6 0+ 6.5 0+ 3.8 14.3+ 1.5

0+ 11.6 0+ 6.3 2.5+ 9.1 0+ 6.7 0+ 4 14+ 6 17+ 7.5 0+ 11.6

0+ 9.8 0+ 10.3 4.2+ 11.6 0+ 10.6 0+ 4 0+ 3.8 0+ 8.6 0+ 7.7

0+ 13.6 0+ 12.1 11.4+ 4.7 0+ 6.5 14+ 6 0+ 3.8 0+ 4.7 7.4+ 4.1

12.5+ 10 12.2+ 2.6 7.7+ 2.9 0+ 3.8 17+ 7.5 0+ 8.6 0+ 4.7 12.5+ 2.5

15.5+ 1.1 0+ 17.9 20.2+ 2 14.3+ 1.5 0+ 11.6 0+ 7.7 7.4+ 4.1 12.5+ 2.5

Figure 1: Fleet Composition.

Figure 2: Vehicle Routing Problem.

number of highway miles and Y is the number of

city miles.

Further, we assume that each service call

requiresapproximately 90 minutes and that each

service agent has to finish his/her route, starting and

ending at the depot, within 8 hours.

We ignore breaks, and assume that there is no

capacity limit on the routes other than the time limit.

We begin by solving the traditional problem of

minimizing the total fleet vehicle miles traveled

(VMT). (In this small problem, this can be done by

explicit enumeration). The total optimum VMT is

97.2. One vehicle visits customers 1, 2, 3, and 4 with

a total travel distance of 47.3 miles, comprised of

22.9 city miles and 24.4 highway miles. The other

vehicle visits customers 5, 6, 7, and 8 with a total

travel distance of 49.9 miles, comprised of 21.9 city

miles and 28 highway miles. The estimated travel

time for the first route is 75 minutes and for the

second route is 78 minutes. Note that in this

variation of the problem, we do not differentiate

between vehicles, as we are simply minimizing

distance traveled.

For illustrative purposes, to estimate fuel

consumption of each vehicle along the given routes

we assume the estimated highway and city MPGs as

defined in Figure 1. (Of course, real-world

calculations are more complex as we discussed in

section 2). As a result, the fuel consumption of the

Taurus for the first route is 2.14 gallons and for the

second route is 2.22 gallons. For the Escape Hybrid,

the first route consumes 1.67 gallons and the second

route consumes 1.77 gallons.

The optimal solution is to assign the Taurus to

the first route, resulting in the consumption of 2.14

gallons, and to assign the Escape to the second route,

with an estimated consumption of 1.67 gallons of

gasoline. The total fleet fuel consumption for the

given solution is 3.81 gallons of gasoline. The

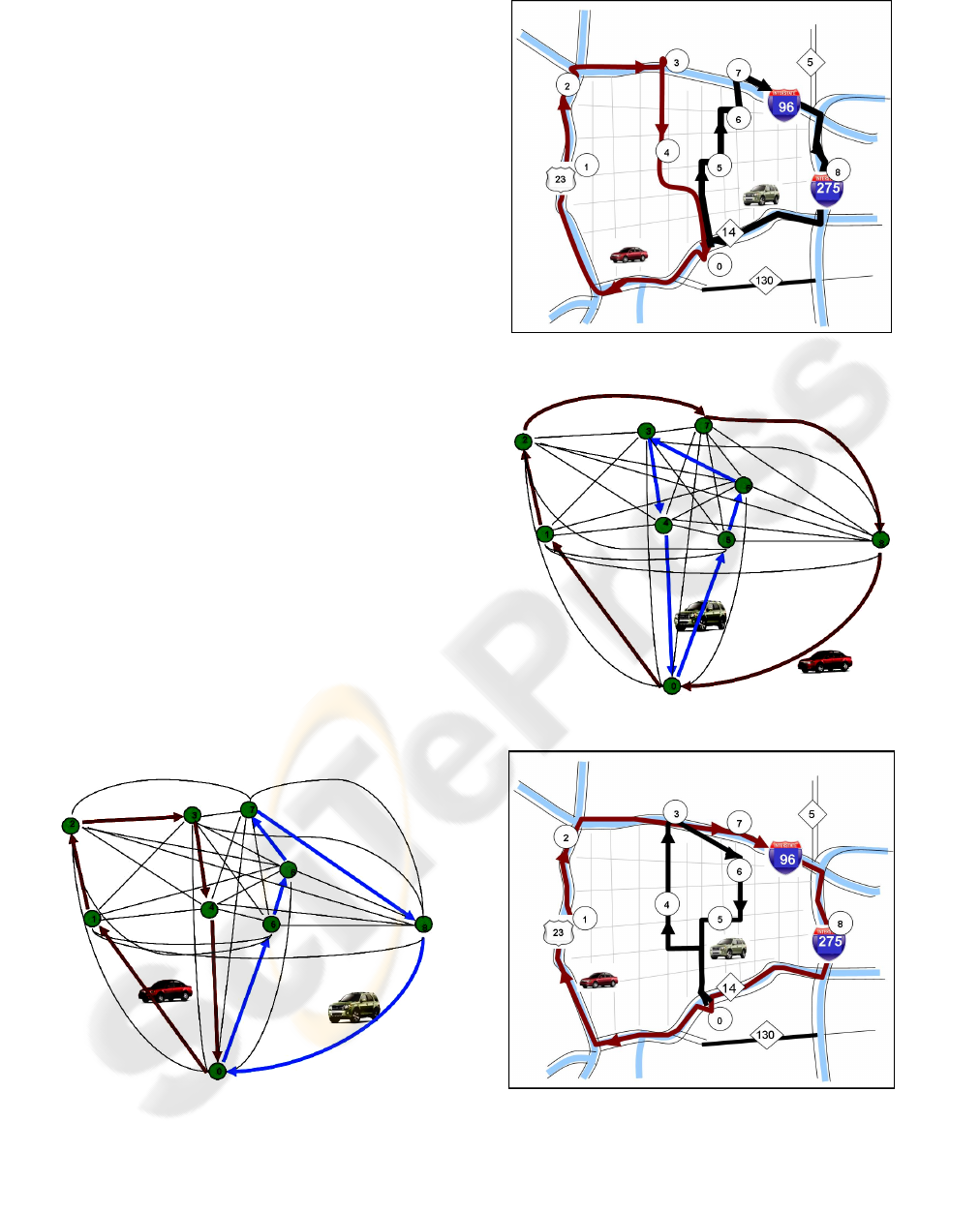
results are presented graphically in Figures 3 and 4.

VEHICLE ROUTING TO MINIMIZE MIXED-FLEET FUEL CONSUMPTION AND ENVIRONMENTAL IMPACT

289

We next reformulate the problem to take into

account fuel economy, i.e. distinguishing in our

optimization between highway and city driving, and

treating the two vehicles separately, in recognition

of their distinct characteristics. The optimal solution

for this problem is presented in Figures 5 and 6.

Although the VMT increases (from 97.2 to

101.7), the fuel consumption decreases from 3.81 to

3.72 gallons. Note that the optimal routes have

changed (see Figure 4). The route served by the

Taurus covers customers 1, 2, 7, and 8 with a total

length of 63.3 miles, but of this 54.4 miles is

highway driving and only 8.9 miles is city driving.

Conversely, the Escape Hybrid is assigned to a route

that serves customers 5, 6, 3, and 4, using only city

driving (for a total length of 38.4 miles).

Table 2 provides a comparative summary of the

two solutions. In addition to the economical impact,

this demonstrates how a reduction in fuel

consumption also leads to a reduction in

environmental impact from the fleet operations. First

of all, the reduction of fuel consumption reduces the

emissions. In addition, the second solution

shifts the time the Taurus spends in the city routes to

the Escape Hybrid. As is shown in Figure 1, the

Taurus has a lower EPA Air Pollution Score than the

Escape Hybrid. Consequently the second solution

also reduces health-damaging and smog-forming

airborne pollutants along populated areas. We could

also capture this explicitly in the objective function

of our formulation, either by specifying constraints

on the total Air Pollution Score (possibly weighted

by the location of the route arcs), or by introducing

weights in the objective function.

Figure 3: Solution 1 Graph.

Figure 4: Solution 1 Map.

Figure 5: Solution 2 Graph.

Figure 6: Solution 2 Map.

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

290

Table 2: Comparative summary of two VRT solutions.

5 CONCLUSIONS

In this paper we discuss the importance of the

heterogeneous fleet vehicle routing problem based

on fuel consumption rather than just distance

traveled. We describe the complex function that

determines how much fuel a given route consumes,

and argue that distance is an inadequate surrogate

when multiple fleet types, especially varying across

different technologies, are used. We provide a

simple example to illustrate how minimizing total

miles traveled can yield a very different solution

than minimizing fuel consumption. We also discuss

solution techniques, specifically based on the use of

composite variable modeling, to solve this

computationally challenging problem.

In the future, we propose to consider emissions

as well as explicit fuel costs (which implicitly

capture CO

emissions but not NO

). We also

suggest extending VRPMF to include variations and

extensions such as those studied in the basic VRP,

such as balancing routes, satisfying time windows,

etc.

REFERENCES

Chan, C. C. and Chau, K.T.; Modern Electric Vehicle

Technology. Oxford University Press Nov. 15, 2001.

Brundell-Freij, K. and Ericsson, E.; Influence of street

characteristics, driver category and car performance on

urban driving patterns, Transportation Research Part D

10, 2005, pp. 213-229.

Tavares, G., Zsigraiova, Z., Semiao, V., Carvalho, M.G ,

Optimization of MSW collection routes for minimum

fuel consumption using 3D GIS modeling, Waste

Management 29, 2009, pp. 1176–1185.

PSAT Overview, January 2008, http://

www.transportation.anl.gov/pdfs/HV/412.pdf

Rose-Hulman Institute of Technology; Rose-Hulman

Institute of Technology Students Design Hybrid

Vehicle Powertrain with Simulink and SimDriveLine,

2005; http:// www.rose-hulman.edu/ challengex/

downloads/Rose-Hulman_user_story.pdf

PTV AG, VISSIM – State-of-the-Art Multi-Modal

Simulation; http:// www. ptvag. com/ fileadmin /

files_ptvag.com/download/traffic/Broschures_Flyer/V

ISSIM/VISSIM_Brochure_e_2009_HiRes.pdf, 2009.

R. Wiedemann, U. Reiter, Wiedemann Model-

Microscopic Traffic Simulation The Simulation

System Mission, 1991; http://

www.ptvamerica.com/fileadmin/files_ptvamerica.com

/library/1970s%20Wiedemann%20VISSIM%20car%2

0following.pdf

Roshan Busawon, M. David Checkel, CALMOB6: A Fuel

Economy and Emissions Tool for Transportation

Planners, presented to the Best Practices in Urban

Transportation Planning session of the 2006 Annual

Conference of the Transportation Association of

Canada, Charlettetown, Price Edward Island, 2006.

Robert B. Noland, Mohammed A. Quddus, Flow

improvements and vehicle emissions: Effects of trip

generation and emission control technology,

Transportation Research Part D 11, 2006, pp. 1-14.

Roberto Baldacci, Maria Battarra, and Daniele Vigo,

Routing a Heterogeneous Fleet of Vehicles in

B. Golden, et al. (Eds), The Vehicle Routing Problem:

Latest Advances and New Challenges, Springer 2008,

pp. 3-27.

Cohn, A. “Composite Variable Modeling for Large-Scale

Problems in Transportation and Logistics,” doctoral

dissertation in Operations Research, Massachusetts

Institute of Technology, advised by Dr. Cynthia

Barnhart, April 2002.

Barlatt A.,Cohn A.,FradkinY., Gusikhin O.; Morford C.,

Using composite variable modeling to achieve realism

and tractability in production planning: An example

from automotive stamping, IIE Transactions, Volume

41, Issue 5, 2009 , pp. 421 – 436.

Desaulniers, G., J. Desrosiers, and M. Solomon, editors.

“A Primer in Column Generation.” Springer US, 2005.

Taillard E. D., A heuristic column generation method for

the heterogeneous VRP, Operations Research --

Recherche opérationnelle 33 (1), 1999, pp. 1-14.

(Publication CRT-96-03, Centre de recherche sur les

transports, Université de Montréal, 1996. Revision

11.2005)

Desrochers, M. and F. Soumis. A Generalization

Generalized Permanent Labeling Algorithm for the

Shortest Path Problem with Time Windows. INFOR

1988 26:191 – 212.

VEHICLE ROUTING TO MINIMIZE MIXED-FLEET FUEL CONSUMPTION AND ENVIRONMENTAL IMPACT

291