PIECEWISE CLASSIFICATION OF ATTACK PATTERNS FOR

EFFICIENT NETWORK INTRUSION DETECTION

Abdelhalim Zaidi, Nazim Agoulmine

LRSM Group, CNRS IBISC Lab, Evry Val d’Essonne University, Evry, France

Tayeb Kenaza

CRIL, Atrois University, Atrois, France

Keywords: Intrusion Detection, String matching, String classification, Common substrings.

Abstract: This paper presents a new scheme to improve the efficiency of pattern matching algorithms. The proposed

approach is based on a piecewise classification of patterns using the common substrings. The main idea is to

split the whole set of patterns into small subsets in accordance to the common substrings and treat the

subsets independently. To reduce the number of patterns to match, we use the common substrings as an

index for the search. We show that are our algorihtm is capable to outcome in term of performance other

reference algorithms, such as Aho-Corasick.

1 INTRODUCTION

With the increase of networks capacities and

bandwidth, the problem of security is becoming

even harder. Indeed, at this speed it is necessary to

have very efficient mechanisms to detect attacks,

virus and worms. During last years, Network based

Intrusion Detection Systems (NIDS) have attracted

significant interest as key enablers of network

security. These systems present powerful tools used

to guaranty high-level security to protect corporate

networks.

A NIDS is a mechanism that tries to detect

unauthorized access to a secure zone. This kind of

access is usually an attempt to compromise the

network and servers activities (Beale, 2007). The

signature based NIDS engine that is used by these

NIDS aims to verify if a set of known malicious

patterns are contained in the inbound stream. Each

pattern describes the signature of known attack that

has been analysed previously. The matching process

executed by the engine, also known as detection

engine, is based on multi-string matching

algorithms. The performance of this type of NIDSs

is therefore highly determined by the performance of

these algorithms. To deal with high throughput and

increasing number of attacks, detection engines have

to improve in performance to be able to verify all

elements of the monitored streams. For that multi-

pattern matching algorithms are required.

In the multi-pattern matching problem, the

objective is to find all occurrences of all the patterns

in the target text. Let P = {p

, p

, ... , p

} be the set of

patterns and T = t

, t

, ..., t

be a large text. Both p

and

T are strings of characters from a fixed alphabet Σ.

Given P and T, the algorithm must locate the

positions of all occurrences of any pattern p

i in T.

In this paper, we present a new design for the

attack-pattern classification that is based on the

common substrings principle. This approach aims to

reduce the number of investigated patterns and to

choose the best search method regarding the length

of common substrings as well as the size of the

pattern’s subset.

The remaining of the paper is as follows, after

this introduction to the paper, the Section 2 presents

a state of art in the area of pattern matching. In

Section 3, we present the problems related to the so

called common substring problem. In the Section 4,

we present our solution whereas Section 5

introduces the experimental results and discuss

them. Finally, we conclude our work and give some

future directions in section 6.

100

Zaidi A., Agoulmine N. and Kenaza T. (2010).

PIECEWISE CLASSIFICATION OF ATTACK PATTERNS FOR EFFICIENT NETWORK INTRUSION DETECTION.

In Proceedings of the International Conference on Security and Cryptography, pages 100-104

DOI: 10.5220/0003033101000104

 SciTePress

2 RELATED WORK

The most well known algorithms for string matching

are those proposed in 1977 by R. Boyer and J.

Moore (BM) (Boyer, 1977) for single matching and

in 1975 by Aho and Corasick (AC) (Aho, 1975) for

multiple matching. The BM algorithm uses two

heuristics: bad characters and good suffix that

reduce the number of comparisons relatively to the

naïve algorithm. BM is not efficient in multiple

strings matching, because it has to perform iterative

search for each pattern. In (Horspool, 1980),

Horspool improved the BM algorithm by proposing

a simpler and more efficient implementation that

uses only the bad-character heuristic.

In contrast to BM, the AC algorithm is an

efficient multi-pattern matching algorithm. Based on

the finite-state automata constructed from the set of

patterns, the AC algorithm can search for all the

patterns in one pass. Flurry of works and

enhancements related to the AC algorithm have been

presented and are widely used in current information

and communication technology.

In 2002 Fisk and Varghese (Fisk, 2002) designed

the Set-wise Boyer-Moore-Horspool algorithm. It is

an adaptation of BM to concurrently match a set of

rules. This algorithm is shown to be faster than both

AC and BM for medium-size pattern sets. Their

experiments suggest triggering a different algorithm

depending on the number of rules: Boyer-Moore-

Horspool if there is only one rule; Set-wise Boyer-

Moore-Horspool if there are between 2 and 100

rules, and AC for more than 100 rules. C. J. Coit, S.

Staniford, and J. McAlerney proposed the AC_BM

algorithm (Coit, 2002), which is similar to the Set-

wise Boyer-Moore-Horspool algorithm.

Using the bad-character heuristic introduced in

the BM algorithm, S. Wu and U. Manber designed

in 1994 the WM multi-pattern matching algorithm

(Wu, 1994). WM uses two or three suffix characters

to generate shift table constructed by preprocessing

all patterns. The algorithm uses a hash table on two

characters prefix to index a group of patterns, used

when the shift is zero. Finally, naïve comparison is

applied to confirm if the pattern exist in the text.

WM deals efficiently with large pattern set size, but

its performance depends on the shortest pattern.

Therefore, the maximum shift is equal to the length

of the shortest pattern minus one.

G. Anagnostakis, E. P. Markatos, S. Antonatos,

and M. Polychronakis proposed the E2XB

algorithm. It is an exclusion-based pattern matching

algorithm (Anagnostakis, 2003) based on the fact

that mismatches are, by far, more common than

matches. This algorithm was designed for providing

quick negatives.

3 COMMON SUBSTRINGS

PROBLEM

This section reviews the main ideas and definitions

underlying the Common Substrings Problem (CSP)

and the string classification problem. CSP is a very

wide known problem in string set theory. Indeed, the

most asked question about a set of string is: what

substrings are common to a large number of strings?

This problem is related to the problem of finding

substrings that appear (occur) repeatedly in a large

text (Gusfield, 1997). In this case, the large text

represents the concatenation of all the strings in the

CSP problem, so the common substrings represent

the substrings that occur repeatedly in the

concatenated text with a distance condition. The

CSP can be used in file comparison, approximate

string matching biological application such as

similarity detection in DNA sequences.

3.1 Formal Definition

The common substring problem can be derived from

the k-common substring problem, which can be

defined as follows:

Let S = {s

, s

…, s

} be the set of K strings. For

2 ≤ k ≤ K, we have to find the length and the longest

common substring to k strings, at least. When k = K,

we have the longest common substring for all the

strings.

Example:

S = {athe, heat, athire, athis, wiathis}; K=5

Table 1: K-common substring solution.

k Length substrings

2 5 athis

3 4 athi

4 3 ath

5 2 at

The common substring is “at” (k = 5 = K).

3.2 Problem Solution

We can locate the length and position of the longest

common substrings either by using the generalized

suffix tree or by dynamic programming (Gusfield,

1997). The running time is, respectively, O(n) and

O(p), where n=Σ|si| and p=∏|si|. We can note that the

PIECEWISE CLASSIFICATION OF ATTACK PATTERNS FOR EFFICIENT NETWORK INTRUSION DETECTION

101

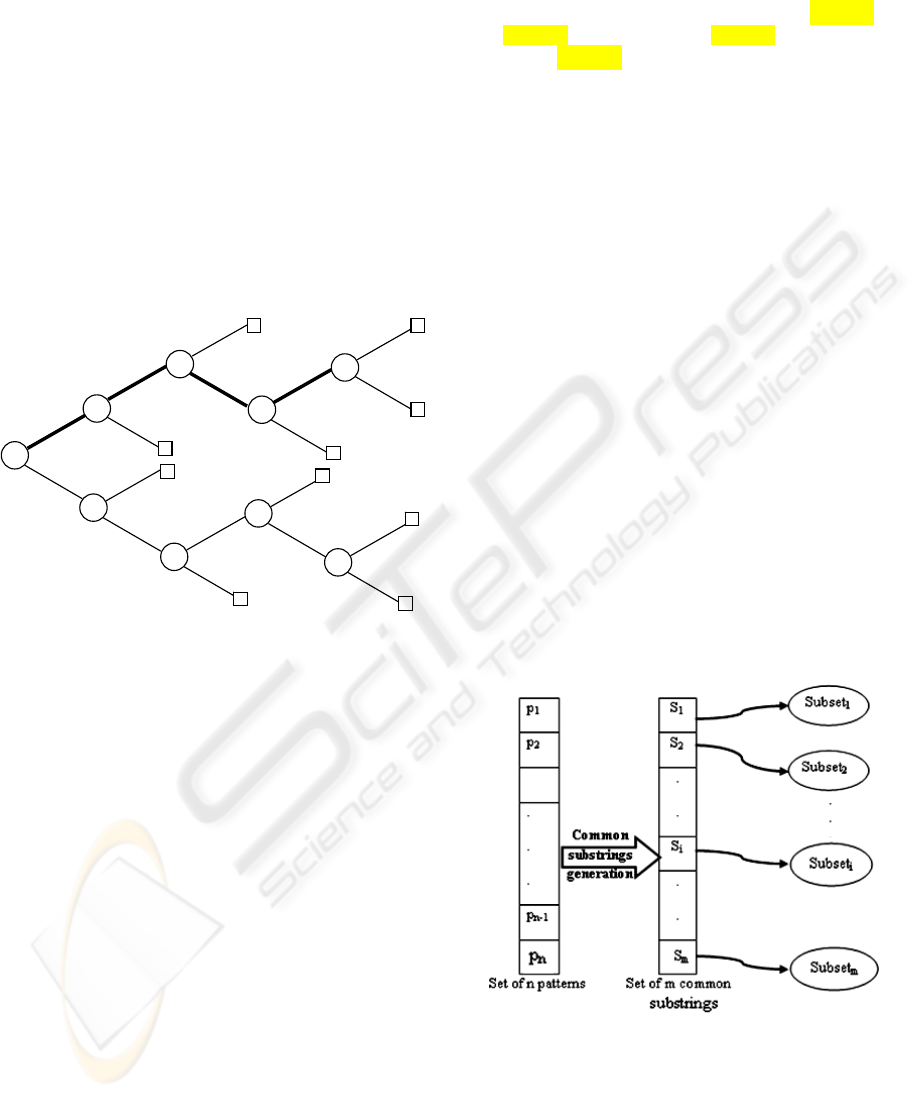
suffix-tree approach provides a linear-time solution

for the CSP. For that raison, we focus our work on it.

An efficient algorithm was proposed in (Gusfield,

1997) with a running time of O(n). The main idea is

to build a generalized suffix tree, to concatenate all

the strings with special separators that represent

terminators, then to find the deepest internal nodes

with a subtree that contains leaves from all the

strings. The longest common substrings are the

strings from the root to the deepest nodes.

The scheme figure 1 present a part of the

generalized suffix tree for the set S = {athe, heat,

athire, athis, viathis}; we use the separator $i for each

string s

in S: athe$1, heat$2, athire$3, athis$4,

viathis$5.

e$1

re$3

e$3

Figure1: Generalized suffix tree.

In this example, the subtree of the node 1

contains the terminators of all the strings, so the

substring “at” is the longest common substring.

Whereas, the node 2 gives the common substring of 4

strings (1, 3, 4 and 5), the nodes 3 and 4 give the

substrings of 3 and 2 strings, respectively.

The result of the algorithm is a table that gives all

the longest common substrings sorted by the number

of strings covered. In our case, as we will explain in

the next section, we change the algorithm output to

give only the result for the maximum covered strings

with a minimum length condition. In the previous

example, if we take 3 as a minimum length so the

maximum strings covered is 4.

4 PROPOSED APPROACH

The main idea of our proposal is that we will use the

fact that many attacks patterns share generally

common substrings, due to the similarities between

attacks and their execution scenarios. For example,

in the four SNORT rules with the SIDs: 6141, 6334,

6291 and 6304 (SNORT, 2009), we have the

common substring “Server” for the four rules

patterns: "R|00|SoftWAR Server",

"R_Server", "BackLash Server" and "from

= JJB + Server" respectively.

So if we find “Server”, we can activate the

subsequent four different rules. Otherwise, we can

eliminate them. This example shows the efficient of

the exclusion method which the main driver of our

proposal. We propose to use the common substring

technique to generate a cover set of the whole

known attack set.

Our approach includes two phases: a

preprocessing phase, where pattern subset classes are

generated, and a searching phase, in which we apply

an adequate pattern-matching algorithm to detect

patterns. The second phase consists of two separate

researching methods: one on the common substrings

set and the other on one of the sub-set of the pattern.

4.1 Preprocessing Phase

The first phase of the approach includes two main

functions. The first generates the common substrings

set of the patterns, and the second splits the whole set

of patterns on small groups based on common

substrings. As illustrated in figure 2, the result of this

phase is a subset partition of the pattern set. Each of

the subset is indexed by a common substring. This

phase is an off-line process, so it does not affect the

detection speed.

Figure 2: Common substrings based classification.

The common substring set is generated using the

Algorithm 1.

SECRYPT 2010 - International Conference on Security and Cryptography

102

4.2 Searching Phase

The searching phase consists of two phases also. The

first one is the detection of common substring in the

text and the second is the matching of patterns

indexed by common substrings detected in the first

step. For the matching process, we propose to use

existing algorithms. Depending on the size of sets

and the mean length of either the common substrings

or the subsets of patterns, we can choose the

adequate pattern matching algorithm.

We propose to use three different algorithms:

BM, AC and WM. The first algorithm (BM), can be

used when we have only one pattern. It is the case

generated by the steps 14, 15 and 16 in Algorithm 1.

The two other algorithms (AC and WM) can be used

when we have more than one pattern to search. AC

can be used when the shortest pattern length in the

subset is less than 5, otherwise we use WM. This

choice is due to the fact that WM is based on the

BM technique (bad-character shift), where the

shortest pattern bounds the shift distance.

The searching method is specified using the

pseudo-code in the algorithm 3.

5 EXPERIMENTAL RESULTS

In order to verify the effectiveness of our approach,

we have conducted a set of experiments to compare

the performance of our solution against the WM

algorithm for several patterns sets. Both algorithms

have been implemented in C++.

The main goal of our experiments is the

comparison of the algorithms performances against

the pattern set size as well as the size of the files that

contain the target text. Because of the system

environment limitation, we have only used only six

common substrings set. In our experiments, we

considered detection time or scanning speed as

performance indicators to compare the algorithms.

Experiments were performed with a randomly

generated text files where specific patterns have

been randomly added in the text file.

In the experiments we use three sets of 1000,

2000 and 3000 patterns and six common substrings

that generate six pattern subsets. We compare the

results of our approach with those of the Wu-

Manber algorithm; we show the results in figures 3,

4 and 5.

Input: a text T of n characters, S the common

substrings, ST the subset of the patterns.

Output: The set of the patterns found in T.

01 Let m be the length of the shortest element in S;

02 If m ≤ 5

03 Aho-Corasick(T, S); //search using AC

04 Else Wu-Manber (T, S); //search using WM

05 For all S

matched

{

06 Let STi be the subset indexed by Si;

07 If size(STi) = 1 Boyer-Moore(T, Si);

//search for one pattern

08 Else {

09 Let d be the length of the shortest

pattern in STi;

10 If d ≤ 5 aho-Corasick(T, STi);

11 Else Wu-Manber(T, STi);

}

Algorithm 2: Searching method.

Input: P a set of n patterns; K the sum of the patterns

lengths; L the maximum length; min the minimum

length

Output: S a set of m common substrings;

01 While P is not empty and L ≥ min

{

02 Use the generalized suffix tree algorithm to generate

T(1..K – 1) the table of the k-common substrings;

03 Find i where the length of the maximum common

substring C in T(i) is L;

04 If i exist

{

05 add C to S;

06 Remove all the patterns concerned from P and add

them to the Subset

;

07 Index the Subset

by C;

08 Let v be the sum of lengths of all patterns removed;

09 K = K – v;

10 j = j +1;

}

11 L = L – 1; // we have to change the maximum length

whether we find i or not

}

12 If L < min // P is not empty

{

13 For each patterns in P

{

14 Let C be the string composed by the L+1 first chars of

the current pattern;

// we suppose that the minimum length in P is greater

than min

15 Add C to S;

16 Index the Subset

by C; // only one element

17 j = j + 1

}

Algorithm 1: Patterns Classification.

PIECEWISE CLASSIFICATION OF ATTACK PATTERNS FOR EFFICIENT NETWORK INTRUSION DETECTION

103

0,01

0,02

0,03

0,04

0,05

0,06

0,07

2347 1059 549 299 154

File size (KB)

Time (s)

Classification

W u Manber

Figure 3: Performances against 1000 patterns.

0,01

0,02

0,03

0,04

0,05

0,06

0,07

0,08

0,09

2347 1059 549 299 154

File size (KB)

Time (s)

Classification

Wu Manber

Figure 4: Performances against 2000 patterns.

0,02

0,04

0,06

0,08

0,1

0,12

0,14

0,16

2347 1059 549 299 154

File size (KB)

Time (s)

Classification

Wu Manber

Figure 5: Performances against 3000 patterns.

These results show that the classification

approach yields a better performance and gives good

results. Our approach decreases the running time by

36%, 43% and 62% for the three cases, respectively

1000, 2000 and 3000 patterns.

6 CONCLUSIONS AND FUTURE

WORK

In this paper, we proposed a scheme to improve the

performance of the pattern matching algorithms. We

introduced a new classification method of the pattern

set based on the common substrings. In our

approach, we split the pattern set into small subsets

according to the common substrings, where each of

them will serve as an index to subset, so every

subset represents a group of patterns with the same

common substring.

Tested against several pattern sets, the results of

the proposed approach are very promising, the

performances are proportional to the size of the

patterns file what represents a good alternative in the

case of the attack data bases of the IDS which are

very increasing. For a robust system evaluation and

as a future work our architecture should be operated

in a real system like the Snort detection engine.

The next step of our work is to implement the

algorithm in an Xilinx Virtex T -5 LXT FPGA

Gigabit Ethernet and test it with high speed access

using the optical interfaces.

REFERENCES

Beale, J et al., 2007. “Snort IDS and IPS Toolkit”.

Syngress, ISBN 1-59749-099-7.

Gusfield, D., 1997. “Algorithms on strings, trees, and

sequences: Computer Science and Computational

Biology”. CAMBRIDGE University Press, ISBN 0-

521-58519-8.

Anagnostakis, K. G, Markatos, E. P, Antonatos, S,

Polychronakis, M., 2003. “E2XB: A domainspecific

string matching algorithm for intrusion detection”. In

Proceedings of the 18th IFIP International

Information SecurityConference (SEC2003).

Wu, S, Manber, Udi., 1994. “A Fast Algorithm For Multi-

Pattern Searching”. Technical Report TR 94-17,

University of Arizona at Tuscon.

Boyer, R. S, Moore, J. S., 1977. “A fast string searching

algorithm”. Communications of the ACM20.

Aho, A. V, Corasick, M. J., 1975, “Efficient string

matching: an aid to bibliographic search”.

Communications of the ACM18.

Horspool, R. N., 1980. “Practical fast searching in

strings”. Software Practice and Experience, vol. 10,

no. 6.

Fisk, M, Varghese, G., 2002. “An analysis of fast string

matching applied to content-based forwarding and

intrusion detection”. Technical Report CS2001-0670

(updated version), University of California - San

Diego.

Coit, C. J, Staniford, S, McAlerney, J., 2002. “Towards

faster pattern matching for intrusion detection, or

exceeding the speed of snort”. In Proceedings of the

2nd DARPA Information Survivability Conference and

Exposition (DISCEX II).

SNORT web site, 2009. www.snort.org

SECRYPT 2010 - International Conference on Security and Cryptography

104